Реализация линейной регрессии своими руками
Добавил пользователь Алексей Ф. Обновлено: 19.09.2024
В этой статье мы расскажем о линейной регрессии — основополагающем алгоритме, с изучения которого начинается любой курс машинного обучения и науки о данных. Лучше всего, конечно, осваивать теорию на реальных проектах, а здесь мы постараемся рассказать о том, что же такое линейная регрессия и в чём её исключительная ценность
- Линейная регрессия: кавер-версия бессмертного хита
- Подготовка к погружению: проверка снаряжения
- Что это?
- Как это работает?
- Линейная регрессия методом обыкновенных наименьших квадратов: начинаем погружение
- Линейная регрессия методом градиентного спуска
- Градиентный спуск, погружение: уровень 1
- Цель обучения алгоритма машинного обучения – минимизировать функцию потерь
- Градиентный спуск, погружение: уровень 2
Кто повторяет старое и узнаёт новое, тот может быть предводителем.
В этой статье мы расскажем о линейной регрессии — основополагающем алгоритме, с изучения которого начинается любой курс машинного обучения и науки о данных. Нелегко писать о столь популярном методе, не переходя сразу же на язык формул. К тому же, как ни странно, большее количество доступной информации не всегда способствует лучшему пониманию. Эффективнее всего, конечно, осваивать теорию на реальных проектах, а здесь мы постараемся как можно подробнее рассказать о том, что же такое линейная регрессия и в чём её исключительная ценность. Материал построен таким образом, чтобы вы сами решили, насколько глубоко хотите погрузиться в тему. Однако этой статьи не будет достаточно, чтобы вы смогли реализовать алгоритм с нуля, её главная цель – ваше интуитивное понимание и, конечно, ваш интерес к проблематике ИИ.
Прежде всего необходимо понимать, что линейная регрессия была разработана еще в XIX веке в области статистики для понимания взаимосвязи между данными ввода и вывода. Объяснимость – это одна из главных ценностей, можно сказать, Священный Грааль машинного обучения, к которому так стремятся исследователи ИИ (тот самый explainable AI). Именно объяснимость позволяет сделать наиболее точный прогноз, чем в первую очередь и занимается область прогнозного моделирования (predictive modeling), этой цели и служит вездесущая минимизация ошибки модели. Где только не применяется прогнозное моделирование данных: в сфере бизнеса и финансов, конечно, маркетинге и продажах, удержании клиентов, алгоритмической торговле; в науке – практически во всех сферах. Лишь бы было достаточное количество численных данных, а в них сейчас недостатка нет. Поэтому линейная регрессия была заимствована из статистики и получила такое широкое распространение в сферах машинного обучения и прогнозного моделирования: быстро, понятно, эффективно, открывает простор для творчества.

Кстати, знаете ли вы разницу между машинным обучением и прогнозным моделированием? Напишите, пожалуйста, в комментариях! Ответ будет в следующей статье цикла. А сейчас предлагаем вам погрузиться глубже в тему линейной регрессии (ассоциации с дайвингом настойчиво преследуют автора этой статьи по неизвестной причине).
Прежде всего давайте убедимся, что вы знакомы с понятиями, без которых дальше не обойтись.
В контексте машинного обучения линейная регрессия относится к разделу обучения с учителем (supervised learning), то есть когда явно прослеживается связь между вводом и выводом и предсказывается некое значение по ограниченному количеству примеров (на которых, как ученик, обучается алгоритм). Напомним, что обучение с учителем, или контролируемое обучение, делится на две категории: регрессия и классификация (о ней в следующих материалах).
Для обучения с учителем данные мы делим на обучающий (training set) и тестовый наборы (testing set): 80/20 – обычное соотношение. Обучающий набор — это данные, на которых алгоритмбудет учиться. Например, при использовании линейной регрессии точки в обучающем наборе используются для построения линии наилучшего соответствия (line of best fit). Тестовый набор будет использован для оценки качества модели.
На основе обучающих данных мы можем построить график (например, количество часов занятий студента на нем будет обозначено x, а его итоговый балл y) и определить функцию, которая будет очень похожа на этот график. Такую функцию называют функцией гипотезы (hypothesis function), в нашем случае это будет одномерная линейная регрессия (с одной переменной). Теперь на основе функции гипотезы можно сделать прогноз.
Точность функции гипотезы может быть измерена с помощью функции стоимости, или функции потерь. Почему она так называется? Потому что она характеризует потери при неправильном принятии решений на основе наблюдаемых данных. Функция потерь принимает разницу между функцией гипотезы при значениях x и обучающей выборкой при тех же значениях x. Мы стремимся найти параметры функции потерь таким образом, чтобы ее выходные данные были минимальны.
Обучение модели – это и есть минимизация функции потерь, а для этого нужно двигаться в отрицательном направлении производной. Так мы сможем найти такую функцию гипотезы, которая точнее описывает наши обучающие данные. Предположим, что это будет одномерная (простая) линейная регрессия.
Линейная регрессия – это модель линейной зависимости одной (зависимой) переменной от другой или нескольких.
Математическое представление линейной регрессии достаточно легко для восприятия. Линия простой линейной регрессии задается уравнением вида y = β0 + β1x, где x – независимая переменная, y – зависимая. Как мы учили в 7 классе!

Простая линейная регрессия с одной независимой переменной (x): красные точки — это реальные значения, линия регрессии (y) — линия наилучшего соответствия, проходящая через точки графика разброса
Наклон линии на этом графике равен коэффициенту β1, точка пересечения (перехват, intercept) определена в коэффициенте β0 (то есть чему равен y при x = 0), этот коэффициент даёт нашей линии свободу передвижения вверх и вниз по двумерному пространству. Алгоритм при обучении стремится найти эти коэффициенты и таким образом определить регрессионную функцию (модель).
Когда на вводе одна переменная (x), это простая линейная регрессия, если их несколько – это уже множественная линейная регрессия. График линейной регрессии в двух измерениях (с единственной независимой переменной) — прямая линия, в трёх — плоскость, в четырёх и более — гиперплоскость.
За этой внешней простотой – огромный потенциал: мы увидим, как на основе этого метода с более чем двухсотлетней историей появилось множество невероятных идей и возможностей. Именно линейная регрессия лежит в основе многих новейших алгоритмов, находящихся на самом острие науки, включая глубокие нейронные сети.
Как уже упоминалось, цель алгоритма линейной регрессии – установить такие коэффициенты, чтобы стало возможно определить данную регрессионную модель, а достигается это в процессе обучения. Для этого существует целый ряд методов, однако наиболее популярные из них — это метод обыкновенных наименьших квадратов и краеугольный камень машинного обучения – градиентный спуск.
Для простоты приведём пример с одной независимой переменной. Предположим, что у нас есть некий набор точек наблюдения. Это может быть площадь квартир, рост людей и т. д., то есть любой фактор (регрессор), влияние которого вы хотите узнать (например, посмотреть зависимость роста и веса, площади жилья и его стоимости и т. д.). Конечно, в реальности чаще принимается во внимание не один фактор, а несколько, но на этот случай у нас есть множественная линейная регрессия.
Данные есть, а теперь вопрос: как прочертить прямую линию, которая была бы максимально приближена к этим точкам наблюдения?
e = y — ŷ (Реальное значение — Прогнозированное значение).

Геометрически это сумма длин отрезков между красными крестиками на графике (реальными значениями) и линией регрессии, которую еще называют линией тренда.

Значения ŷ лежат на линии регрессии, а красные крестики обозначают y. e = y — ŷ (Реальное значение — Прогнозированное значение)
Сумма отклонений возводится в квадрат (SSE — sum of squared errors) и минимизируется с помощью дифференциальных и матричных вычислений, которые мы, пожалуй, приводить не будем. Иногда минимизируется не сумма квадратичных отклонений, а среднеквадратичное значение отклонений (MSE — mean of squared errors).
Почему именно квадрат? Я всегда считала, что это делается для избавления от отрицательных значений, однако оказывается, что квадрат длин даёт гладкую функцию (которая имеет непрерывную производную), в то время как просто длина даёт функцию в виде конуса, недифференцируемую в точке минимума. (На тот случай, если любознательность тоже заводит вас далеко).
Метод наименьших квадратов, помимо очевидных достоинств, имеет и существенный недостаток – он плохо справляется с большим количеством данных на вводе (факторов, или попросту xi). Если вы работаете с большими данными, ваш выбор – это градиентный спуск. Используя этот метод, вы занимаетесь машинным обучением в его классическом виде, потому что именно так обучаются нейросети, включая и сверхсовременные алгоритмы глубокого обучения, которые сейчас на самом острие науки.
Представьте себе, что вы стоите на вершине оврага и хотите спуститься вниз, но не знаете как. Вы будете шагать шире, когда склон более пологий, и мельче, когда склон более крутой. Ваш следующий шаг будет зависеть от предыдущего, а достигнув дна оврага, вы остановитесь. Этот образ поможет вам понять дальнейшие объяснения. Крутизну, или уклон, вашего оврага (крутизну в её первоначальном смысле, конечно!) и будет задавать градиент. Градиент, или уклон (slope), — это не что иное, как отношение изменений по оси y к изменениям по оси x.
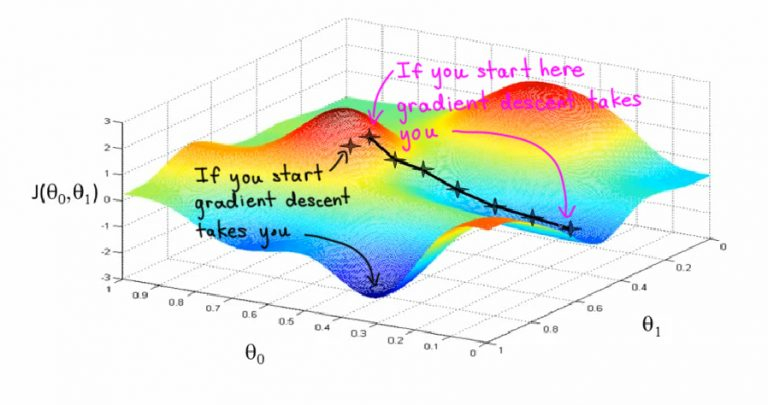
Градиентный спуск – это основной метод обучения нейронных сетей, с его помощью постепенно уточняются параметры нейронной сети (веса и смещение), чтобы таким образом минимизировать функцию потерь сети (cost function, loss function)
Цель обучения алгоритма машинного обучения – минимизировать функцию потерь
(Напоминаем, функция потери — разница между значениями меток обучения и прогноза, сделанного с помощью модели). Как это происходит?
Если говорить о простой линейной регрессии ( y = β0 + β1 x) в терминах машинного обучения, смещение (intercept) соответствует параметру β0, а вес (weight) – параметру β1. Сначала инициируются случайные значения для каждого коэффициента. Сумма квадратов ошибок вычисляется для каждой пары входных и выходных значений. Градиент ошибки будет подсчитываться с использованием частных производных функции потерь по весам и смещению.
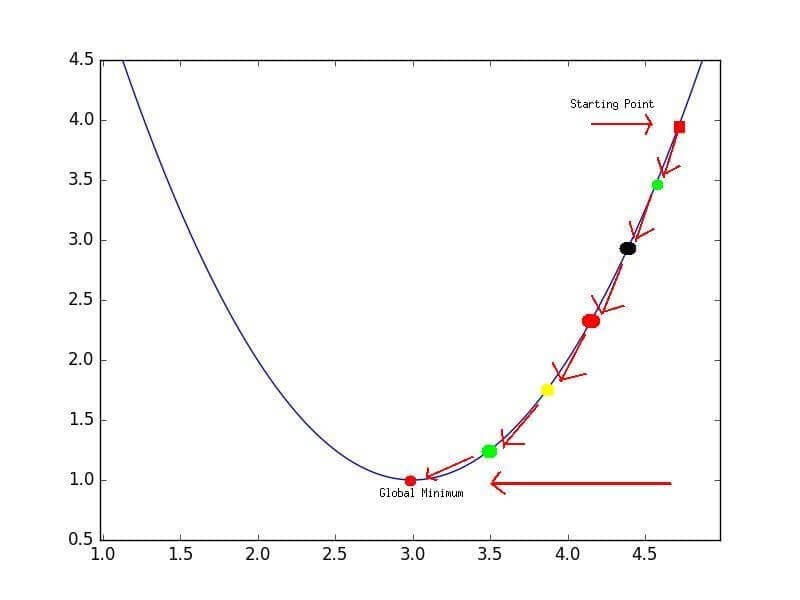
Нам понадобится ещё коэффициент скорости обучения (learning rate), он также задается эмпирически. Этот параметр (обычно обозначается £), определяет размер шага по градиенту, выполняемого на каждой итерации, и отвечает за то, как будут корректироваться веса с учётом функции потерь. Чем меньше значение скорости обучения, тем медленнее движение по градиенту. При малом коэффициенте скорости обучения мы, скорее всего, не пропустим ни одной впадины (локального минимума), хотя рискуем застрять на плато, и тогда сходимости придётся подождать.
Процесс повторяется до тех пор, пока не будет достигнута минимальная сумма квадратов ошибок или пока не станет невозможным дальнейшее улучшение.
Градиентный спуск — это итеративный метод нахождения локального минимума функции с помощью движения вдоль градиента.
Давайте используем градиентный спуск для обучения простой линейной регрессии. Функцией гипотезы тогда будет линейная функция


Необходимо определить параметры нашей функции гипотезы с помощью функции стоимости, заданной таким образом:

Мы делим на m наши примеры из обучающего набора, обратите внимание, что двойка в знаменателе — это математическая уловка, которую мы используем, чтобы потом компенсировать 2 при взятии производной функции. В скобках разность реальных значений и прогнозов, потом вся она суммируется и возводится в квадрат.
Теперь нужно минимизировать функцию относительно её параметров:

Для простой линейной регрессии эти параметры можно установить равными нулю, а в случае множественной надо будет задать им случайные величины. Подбор параметров осуществляется путем итерации по нашему обучающему набору. Мы будем обновлять параметры согласно такой формуле:


где α – скорость обучения, а – производная, или уклон, функции стоимости, что даёт нам при подстановке

С каждой итерацией параметры будут обновляться, а функция будет стремиться к минимуму.
Вышеописанный алгоритм в англоязычных источниках называется Batch Gradient Descent, поскольку на каждой итерации задействуется весь обучающий набор (batch). Однако существуют такие разновидности этого алгоритма, как стохастический градиентный спуск и мини-пакетный градиентный спуск. Возможно, у вас возникнет желание ознакомиться с ними.
В машинном обучении и в статистическом моделировании эта взаимосвязь используется для прогнозирования результатов будущих событий.
Линейная регрессия
Линейная регрессия использует отношения между точками данных, чтобы провести прямую линию через все они.
Эта линия может использоваться для прогнозирования будущих значений.
В машинном обучении очень важно предсказывать будущее.
Как это работает?
В Python есть методы для поиска взаимосвязи между точками данных и построения линии линейной регрессии. Мы вам покажем как использовать эти методы вместо того, чтобы перебирать математические формулы.
В приведенном ниже примере ось X представляет возраст, а ось Y представляет скорость. Мы зарегистрировали возраст и скорость 13 машин, проезжающих мимо. городская тюрьма. Давайте посмотрим, можно ли использовать собранные нами данные в линейном регресс:
Пример
Start by drawing a scatter plot:
import matplotlib.pyplot as plt
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
plt.scatter(x, y)
plt.show()
Result:

Пример
Import scipy and draw the line of Linear Regression:
import matplotlib.pyplot as plt
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x):
return slope * x + intercept
mymodel = list(map(myfunc, x))
plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()
Result:

Объяснение примера
Импортируйте нужные вам модули.
Вы можете узнать о модуле Matplotlib в нашем Руководстве по Matplotlib.
Вы можете узнать о модуле SciPy в нашем руководстве по SciPy.
import matplotlib.pyplot as plt
from scipy import stats
Создайте массивы, представляющие значения осей x и y:
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
Выполните метод, который возвращает некоторые важные ключевые значения линейной регрессии:
slope, intercept, r, p, std_err = stats.linregress(x, y)
Создайте функцию, которая использует наклон и перехватить значения, чтобы вернуть новое значение. Этот новое значение представляет, где по оси Y будет соответствующее значение x. размещено:
def myfunc(x):
return slope * x + intercept
Пропустите каждое значение массива x через функцию. Это приведет к новому массив с новыми значениями для оси Y:
mymodel = list(map(myfunc, x))
Нарисуйте исходную диаграмму рассеяния:
Проведите линию линейной регрессии:
R для отношений
Важно знать, как взаимосвязь между ценностями ось x и значения оси y, если нет связи, линейная регрессию нельзя использовать для предсказания чего-либо.
Эта связь - коэффициент корреляции - называется r .
Значение r находится в диапазоне от -1 до 1, где 0 означает отсутствие связи, а 1 (и -1) означает 100% связанных.
Python и модуль Scipy вычислит это значение за вас, все, что вам нужно do снабжает его значениями x и y.
Пример
How well does my data fit in a linear regression?
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
Примечание. Результат -0,76 показывает, что существует связь, не идеально, но это указывает на то, что мы могли бы использовать линейную регрессию в будущем предсказания.
Предсказать будущие ценности
Теперь мы можем использовать собранную информацию для прогнозирования будущих значений.
Пример: давайте попробуем предсказать скорость автомобиля 10-летней давности.
Для этого нам понадобится та же функция myfunc() . из приведенного выше примера:
def myfunc(x):
return slope * x + intercept
Пример
Predict the speed of a 10 years old car:
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x):
return slope * x + intercept
Пример предсказал скорость на уровне 85,6, что мы также могли прочитать из диаграмма:
Плохо подходит?
Давайте создадим пример, где линейная регрессия не будет лучшим методом предсказывать будущие ценности.
Пример
These values for the x- and y-axis should result in a very bad fit for linear regression:
import matplotlib.pyplot as plt
from scipy import stats
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x):
return slope * x + intercept
mymodel = list(map(myfunc, x))
plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()
Result:

А r для отношения?
Пример
You should get a very low r value.
import numpy
from scipy import stats
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
slope, intercept, r, p, std_err = stats.linregress(x, y)
Результат: 0,013 указывает на очень плохую взаимосвязь и говорит нам, что этот набор данных не подходит для линейной регрессии.
Вопросы пользователей по теме Python
Цель состоит в том, чтобы вычесть строку (N) с предыдущей строкой (N-1), разделенной группами. Учитывая df years nchar nval 0 2019 a 1 1 2019 b 1 2 2019 c 1 3 2020 a 1 4 2020 s 4 Давайте разделим на группу года 2019 и обозначим его как df_2019 Д.
Поэтому я пытаюсь написать код python с некоторыми веб-скрапами и материалами excel (проверка еженедельных цен на недвижимость), и у меня есть некоторые функции около 6, которые мне нужно выполнить, в основном для циклов. Моя проблема в том, что первая функция очищает сайт и добавляет найденные эле.
Как вы можете определить в Python3 класс MyClass так, чтобы вы создавали его экземпляр как obj = MyClass(param1, param2), а затем использовать его для вычисления такой операции, как res = obj(in1, in2, in3) ? Например, с помощью PyTorch вы можете объявить модель как mod = MyResNet50(), а затем вычи.
a='sadfaad' b=[] b.append(x for x in a) print(b) Он возвращается [ at 0x000002042A1DA5F0>] Что знать, почему так происходит? и как мы можем использовать понимание списка для этого.
Кто-нибудь знает, как я могу получить заголовок столбца для моего первого столбца. Колонка v1? v1 = ['AAPL','MSFT','TSLA','FB','BRK-B','TSM','NVDA','V','JNJ','JPM','WMT','PG','BAC','HD','BABA','TM','XOM','PFE','DIS','KO'] Код import pandas as pd from bs4 import BeautifulSoup as bs import request.
Я хочу проверить, меньше ли элемент в списке, чем следующий, и сломать функцию в тот момент, когда это не так. Я написал этот код, и я не уверен, что не так, потому что вывод [1], а должен быть [1, 3, 4, 5, 6, 7]. Вероятно, это небольшая ошибка, но мне не у кого спросить. def check_order(a): i =.

Линейная регрессия ( Linear regression ) — модель зависимости переменной x от одной или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости.
Применение линейной регрессии
Предположим, нам задан набор из 7 точек (таблица ниже).

Цель линейной регрессии — поиск линии, которая наилучшим образом соответствует этим точкам. Напомним, что общее уравнение для прямой есть f (x) = m⋅x + b, где m — наклон линии, а b — его y-сдвиг. Таким образом, решение линейной регрессии определяет значения для m и b, так что f (x) приближается как можно ближе к y. Попробуем несколько случайных кандидатов:

Довольно очевидно, что первые две линии не соответствуют нашим данным. Третья, похоже, лучше, чем две другие. Но как мы можем это проверить? Формально нам нужно выразить, насколько хорошо подходит линия, и мы можем это сделать, определив функцию потерь.
Функция потерь — метод наименьших квадратов
Функция потерь — это мера количества ошибок, которые наша линейная регрессия делает на наборе данных. Хотя есть разные функции потерь, все они вычисляют расстояние между предсказанным значением y( х) и его фактическим значением. Например, взяв строку из среднего примера выше, f(x)=−0.11⋅x+2.5, мы выделяем дистанцию ошибки между фактическими и прогнозируемыми значениями красными пунктирными линиями.

Одна очень распространенная функция потерь называется средней квадратичной ошибкой (MSE). Чтобы вычислить MSE, мы просто берем все значения ошибок, считаем их квадраты длин и усредняем.
Вычислим MSE для каждой из трех функций выше: первая функция дает MSE 0,17, вторая — 0,08, а третья — 0,02. Неудивительно, что третья функция имеет самую низкую MSE, подтверждая нашу догадку, что это линия наилучшего соответствия.
Рассмотрим приведенный ниже рисунок, который использует две визуализации средней квадратичной ошибки в диапазоне, где наклон m находится между -2 и 4, а b между -6 и 8.

Слева: диаграмма, изображающая среднеквадратичную ошибку для -2≤m≤4, -6≤p≤8 Справа: тот же рисунок, но визуализирован как контурный график, где контурные линии являются логарифмически распределенными поперечными сечениями высоты.
Глядя на два графика, мы видим, что наш MSE имеет форму удлиненной чаши, которая, по-видимому, сглаживается в овале, грубо центрированном по окрестности (m, p) ≈ (0.5, 1.0). Есл и мы построим MSE линейной регрессии для другого датасета, то получим аналогичную форму. Поскольку мы пытаемся минимизировать MSE, наша цель — выяснить, где находится самая низкая точка в чаше.
Больше размерностей
Вышеприведенный пример очень простой, он имеет только одну независимую переменную x и два параметра m и b. Что происходит, когда имеется больше переменных? В общем случае, если есть n переменных, их линейная функция может быть записана как:
Добавление измерений, на первый взгляд, ужасное усложнение проблемы, но оказывается, постановка задачи остается в точности одинаковой в 2, 3 или в любом количестве измерений. Существует функция потерь, которая выглядит как чаша — гипер-чаша! И, как и прежде, наша цель — найти самую нижнюю часть этой чаши, объективно наименьшее значение, которое функция потерь может иметь в отношении выбора параметров и набора данных.
Итак, как мы вычисляем, где именно эта точка на дне? Распространенный подход — обычный метод наименьших квадратов, который решает его аналитически. Когда есть только один или два параметра для решения, это может быть сделано вручную, и его обычно преподают во вводном курсе по статистике или линейной алгебре.
Проклятие нелинейности
Увы, обычный МНК не используют для оптимизации нейронных сетей, поэтому решение линейной регрессии будет оставлено как упражнение, оставленное читателю. Причина, по которой линейную регрессию не используют, заключается в том, что нейронные сети нелинейны.
Различие между линейными уравнениями, которые мы составили, и нейронной сетью — функция активации (например, сигмоида, tanh, ReLU или других).
Минимум функции

Линейная регрессия – один из важнейших статисических методов, позволяющих прогнозировать значения зависимой переменной, используя значения одной или нескольких независимых переменных.
Построить линию регрессии с помощью Python можно несколькими способами, каждый из которых имеет свои плюсы и минусы, например можно воспользоваться инструментарием библиотеки scikit-learn, методом scipy.polyfit или numpy.polyfit.
В данной статье рассматривается один из вариантов построения линии регрессии с помощью функции stats.lingress стандартной библиотеки scipy.

Stats.lingress – функция, оптимизированная для вычисления линейной регрессии методом наименьших квадратов на вход которой можно подать только два набора измерений. С помощью этой функции вы не сможете получить обобщенную линейную модель или рассчитать многовариантную регрессию, но при всех вышеперечисленных минусах данная функция ‑ один самых быстрых методов расчета простой линейной регрессии, среди других вариантов, предлагаемых python. Так что, если у вас большой объем данных – использование stats.lingress позволит сэкономить на времени вычислений.
В качестве примера сгенерируем два набора измерений, один из которых зависит от другого:
Если данные будут анализироваться с учетом последовательности их регистрации (скажем данные были записаны с определенным шагом по времени), можно добавить еще одну переменную к нашему набору данных
Собственно, сам расчет коэффициентов для линии регрессии и ее статистических показателей выражается следующей строкой кода:
Для вывода линии регрессии на кроссплоте добавляем:
Следующим шагом настраиваем визуализацию, где помимо прочего выведем значение R 2
Параметр r_value можно использовать в качестве количественной оценки того, насколько хорошо расчитанная нами линия регрессии соответствует данным. Значение R 2 будет находится в интервале от 0 до 1, соответственно, чем ближе это значение к единице, тем более достоверна будет оценка, если мы воспользуемся расчитанным уравнением регрессии для прогнозирования
Читайте также:

