Как сделать сложную функцию

Добавил пользователь Валентин П.
Обновлено: 04.10.2024

На данном уроке мы научимся находить производную сложной функции. Урок является логическим продолжением занятия Как найти производную?, на котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Таким образом, если с производными функций у Вас не очень или какие-нибудь моменты данной статьи будут не совсем понятны, то сначала ознакомьтесь с вышеуказанным уроком. Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.

На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.

Смотрим в таблицу на правило (№ 5) дифференцирования сложной функции:

Разбираемся. Прежде всего, обратим внимание на запись . Здесь у нас две функции – и , причем функция , образно говоря, вложена в функцию . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.

Функцию я буду называть внешней функцией, а функцию – внутренней (или вложенной) функцией.

Для того, чтобы прояснить ситуацию, рассмотрим:

Найти производную функции

В данном примере уже из моих объяснений интуитивно понятно, что функция – это сложная функция, причем многочлен является внутренней функцией (вложением), а – внешней функцией.

Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.

В случае простых примеров вроде понятно, что под синус вложен многочлен . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.

Представим, что нам нужно вычислить на калькуляторе значение выражения при (вместо единицы может быть любое число).

Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: , поэтому многочлен и будет внутренней функцией :

Во вторую очередь нужно будет найти , поэтому синус – будет внешней функцией:

После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции .

Начинаем решать. Из урока Как найти производную? мы помним, что оформление решения любой производной всегда начинается так – заключаем всю функцию в скобки и ставим справа вверху штрих:

Обратите внимание, что внутренняя функция не изменилась, её мы не трогаем.

Ну и совершенно очевидно, что

Результат применения формулы в чистовом оформлении выглядит так:

Далее мы берем производную внутренней функции, она очень простая:

Постоянный множитель обычно выносят в начало выражения:

Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Найти производную функции

Как всегда записываем:

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?

а) Найти производную функции

б) Найти производную функции

Найти производную функции

Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:

Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :

Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:

Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного , но такое решение будет выглядеть ~~как извращение~~ необычно. Вот характерный пример:

Найти производную функции

Здесь можно использовать правило дифференцирования частного , но гораздо выгоднее найти производную через правило дифференцирования сложной функции:

Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:

Косинус – внутренняя функция, возведение в степень – внешняя функция.
Используем наше правило :

Находим производную внутренней функции, косинус сбрасываем обратно вниз:

Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

До сих пор мы рассматривали случаи, когда у нас в сложной функции было только одно вложение. В практических же заданиях часто можно встретить производные, где, как матрёшки, одна в другую, вложены сразу 3, а то и 4-5 функций.

Найти производную функции

Разбираемся во вложениях этой функции. Пробуем вычислить выражение с помощью подопытного значения . Как бы мы считали на калькуляторе?

Сначала нужно найти , значит, арксинус – самое глубокое вложение:

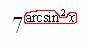
Затем этот арксинус единицы следует возвести в квадрат :

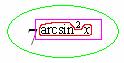
И, наконец, семерку возводим в степень :

То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.

Под штрихом у нас снова сложная функция! Но она уже проще. Легко убедиться, что внутренняя функция – арксинус, внешняя функция – степень. Согласно правилу дифференцирования сложной функции сначала нужно взять производную от степени:

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

На практике правило дифференцирования сложной функции почти всегда применяется в комбинации с остальными правилами дифференцирования.

Найти производную функции

Сначала используем правило дифференцирования суммы , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу :

В обоих слагаемых под штрихами у нас находится произведение функций, следовательно, нужно дважды применить правило :

Замечаем, что под некоторыми штрихами у нас находятся сложные функции , . Каламбур, но это простейшие из сложных функций, и при определенном опыте решения производных Вы будете легко находить их устно.
А пока запишем подробно, согласно правилу , получаем:

! Обратите внимание на приоритет (порядок) применения правил: правило дифференцирования сложной функции применяется в последнюю очередь.

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Пожалуй, хватит на сегодня. Хочется еще привести пример с дробью и сложной функцией, но такой пример принципиально ничем не отличается от двух последних заданий, единственное отличие – вместо правила применяем правило .

Для закрепления темы рекомендую статью Сложные производные. Логарифмическая производная. Помимо рассмотрения дополнительных примеров, есть и новый материал! После изучения третьего урока вы будете очень уверенно себя чувствовать в ходе дальнейшего изучения математического анализа. Если задания покажутся слишком трудными (у всех разный уровень подготовки), то сначала посетите страницу Простейшие типовые задачи с производной, там рассмотрено ещё порядка 15 производных.

Пример 4: Указание: перед дифференцированием необходимо перенести степень наверх, сменив у показателя знак .

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

В этой статье мы будем говорить о таком важном математическом понятии, как сложная функция, и учиться находить производную сложной функции.

Прежде чем учиться находить производную сложной функции, давайте разберемся с понятием сложной функции, что это такое, "с чем ее едят", и "как правильно ее готовить".

Рассмотрим произвольную функцию, например, такую:

Заметим, что аргумент , стоящий в правой и левой части уравнения функции - это одно и то же число, или выражение.

Вместо переменной мы можем поставить, например, такое выражение: . И тогда мы получим функцию

Назовем выражение промежуточным аргументом, а функцию - внешней функцией. Это не строгие математические понятия, но они помогают уяснить смысл понятия сложной функции.

Строгое определение понятия сложной функции звучит так:

Пусть функция определена на множестве и - множество значений этой функции. Пусть, множество (или его подмножество) является областью определения функции . Поставим в соответствие каждому из число . Тем самым на множестве будет задана функция . Ее называют композицией функций или сложной функцией.

В этом определении, если пользоваться нашей терминологией, - внешняя функция, - промежуточный аргумент.

Производная сложной функции находится по такому правилу:

Чтобы было более понятно, я люблю записывать это правило в виде такой схемы:

В этом выражении с помощью обозначена промежуточная функция.

Итак. Чтобы найти производную сложной функции, нужно

1. Определить, какая функция является внешней и найти по таблице производных соответствующую производную.

2. Определить промежуточный аргумент.

В этой процедуре наибольшие затруднения вызывает нахождение внешней функции. Для этого используется простой алгоритм:

а. Запишите уравнение функции.

б. Представьте, что вам нужно вычислить значение функции при каком-то значении х. Для этого вы подставляете это значение х в уравнение функции и производите арифметические действия. То действие, которое вы делаете последним и есть внешняя функция.

Например, в функции

последнее действие - возведение в степень.

Найдем производную этой функции. Для этого запишем промежуточный аргумент

^2" />
как

Ищем в таблице производных производную показательной функции:

(1)

таблице производных производную синуса:

Подставим полученное значение производной в выражение (1):

И, наконец, упростим выражение, вспомнив формулу синуса двойного аргумента:

Заметим, что функции иногда похожи на матрешку: промежуточный аргумент сам является сложной функции. Но тогда при нахождении производной промежуточного аргумента, нужно вновь применить правило нахождения производной сложной функции.

Функции сложного вида не всегда подходят под определение сложной функции. Если имеется функция вида y = sin x - ( 2 - 3 ) · a r c t g x x 5 7 x 10 - 17 x 3 + x - 11 , то ее нельзя считать сложной в отличие от y = sin 2 x .

Данная статья покажет понятие сложной функции и ее выявление. Поработаем с формулами нахождения производной с примерами решений в заключении. Применение таблицы производных и правила дифференцирования заметно уменьшают время для нахождения производной.

Основные определения

Сложной функцией считается такая функция, у которой аргумент также является функцией.

Обозначается это таким образом: f ( g ( x ) ) . Имеем, что функция g ( x ) считается аргументом f ( g ( x ) ) .

Если есть функция f и является функцией котангенса, тогда g ( x ) = ln x – это функция натурального логарифма. Получаем, что сложная функция f ( g ( x ) ) запишется как arctg(lnx). Или функция f , являющаяся функцией возведенной в 4 степень, где g ( x ) = x 2 + 2 x - 3 считается целой рациональной функцией, получаем, что f ( g ( x ) ) = ( x 2 + 2 x - 3 ) 4 .

Очевидно, что g ( x ) может быть сложной. Из примера y = sin 2 x + 1 x 3 - 5 видно, что значение g имеет кубический корень с дробью. Данное выражение разрешено обозначать как y = f ( f 1 ( f 2 ( x ) ) ) . Откуда имеем, что f – это функция синуса, а f 1 - функция, располагаемая под квадратным корнем, f 2 ( x ) = 2 x + 1 x 3 - 5 - дробная рациональная функция.

Степень вложенности определено любым натуральным числом и записывается как y = f ( f 1 ( f 2 ( f 3 ( . . . ( f n ( x ) ) ) ) ) ) .

Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида

( f ( g ( x ) ) ) ' = f ' ( g ( x ) ) · g ' ( x )

Примеры

Найти производную сложной функции вида y = ( 2 x + 1 ) 2 .

Решение

По условию видно, что f является функцией возведения в квадрат, а g ( x ) = 2 x + 1 считается линейной функцией.

Применим формулу производной для сложной функции и запишем:

f ' ( g ( x ) ) = ( ( g ( x ) ) 2 ) ' = 2 · ( g ( x ) ) 2 - 1 = 2 · g ( x ) = 2 · ( 2 x + 1 ) ; g ' ( x ) = ( 2 x + 1 ) ' = ( 2 x ) ' + 1 ' = 2 · x ' + 0 = 2 · 1 · x 1 - 1 = 2 ⇒ ( f ( g ( x ) ) ) ' = f ' ( g ( x ) ) · g ' ( x ) = 2 · ( 2 x + 1 ) · 2 = 8 x + 4

Необходимо найти производную с упрощенным исходным видом функции. Получаем:

y = ( 2 x + 1 ) 2 = 4 x 2 + 4 x + 1

Отсюда имеем, что

y ' = ( 4 x 2 + 4 x + 1 ) ' = ( 4 x 2 ) ' + ( 4 x ) ' + 1 ' = 4 · ( x 2 ) ' + 4 · ( x ) ' + 0 = = 4 · 2 · x 2 - 1 + 4 · 1 · x 1 - 1 = 8 x + 4

При решении задач такого вида важно понимать, где будет располагаться функция вида f и g ( x ) .

Следует найти производные сложных функций вида y = sin 2 x и y = sin x 2 .

Решение

Первая запись функции говорит о том, что f является функцией возведения в квадрат, а g ( x ) – функцией синуса. Тогда получим, что

y ' = ( sin 2 x ) ' = 2 · sin 2 - 1 x · ( sin x ) ' = 2 · sin x · cos x

Вторая запись показывает, что f является функцией синуса, а g ( x ) = x 2 обозначаем степенную функцию. Отсюда следует, что произведение сложной функции запишем как

y ' = ( sin x 2 ) ' = cos ( x 2 ) · ( x 2 ) ' = cos ( x 2 ) · 2 · x 2 - 1 = 2 · x · cos ( x 2 )

Формула для производной y = f ( f 1 ( f 2 ( f 3 ( . . . ( f n ( x ) ) ) ) ) ) запишется как y ' = f ' ( f 1 ( f 2 ( f 3 ( . . . ( f n ( x ) ) ) ) ) ) · f 1 ' ( f 2 ( f 3 ( . . . ( f n ( x ) ) ) ) ) · · f 2 ' ( f 3 ( . . . ( f n ( x ) ) ) ) · . . . · f n ' ( x )

Найти производную функции y = sin ( ln 3 a r c t g ( 2 x ) ) .

Решение

Данный пример показывает сложность записи и определения расположения функций. Тогда y = f ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) обозначим, где f , f 1 , f 2 , f 3 , f 4 ( x ) является функцией синуса, функцией возведения в 3 степень, функцией с логарифмом и основанием е , функцией арктангенса и линейной.

Из формулы определения сложной функции имеем, что

y ' = f ' ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) · f 1 ' ( f 2 ( f 3 ( f 4 ( x ) ) ) ) · · f 2 ' ( f 3 ( f 4 ( x ) ) ) · f 3 ' ( f 4 ( x ) ) · f 4 ' ( x )

Получаем, что следует найти

f ' ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) в качестве производной синуса по таблице производных, тогда f ' ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) = cos ( ln 3 a r c t g ( 2 x ) ) .
f 1 ' ( f 2 ( f 3 ( f 4 ( x ) ) ) ) в качестве производной степенной функции, тогда f 1 ' ( f 2 ( f 3 ( f 4 ( x ) ) ) ) = 3 · ln 3 - 1 a r c t g ( 2 x ) = 3 · ln 2 a r c t g ( 2 x ) .
f 2 ' ( f 3 ( f 4 ( x ) ) ) в качестве производной логарифмической, тогда f 2 ' ( f 3 ( f 4 ( x ) ) ) = 1 a r c t g ( 2 x ) .
f 3 ' ( f 4 ( x ) ) в качестве производной арктангенса, тогда f 3 ' ( f 4 ( x ) ) = 1 1 + ( 2 x ) 2 = 1 1 + 4 x 2 .
При нахождении производной f 4 ( x ) = 2 x произвести вынесение 2 за знак производной с применением формулы производной степенной функции с показателем, который равняется 1 , тогда f 4 ' ( x ) = ( 2 x ) ' = 2 · x ' = 2 · 1 · x 1 - 1 = 2 .

Производим объединение промежуточных результатов и получаем, что

y ' = f ' ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) · f 1 ' ( f 2 ( f 3 ( f 4 ( x ) ) ) ) · · f 2 ' ( f 3 ( f 4 ( x ) ) ) · f 3 ' ( f 4 ( x ) ) · f 4 ' ( x ) = = cos ( ln 3 a r c t g ( 2 x ) ) · 3 · ln 2 a r c t g ( 2 x ) · 1 a r c t g ( 2 x ) · 1 1 + 4 x 2 · 2 = = 6 · cos ( ln 3 a r c t g ( 2 x ) ) · ln 2 a r c t g ( 2 x ) a r c t g ( 2 x ) · ( 1 + 4 x 2 )

Разбор таких функций напоминает матрешки. Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.

Существуют некоторые различия сложного вида от сложных функций. При явном умении это различать, нахождение производных будет давать особенно легко.

Необходимо рассмотреть на приведении подобного примера. Если имеется функция вида y = t g 2 x + 3 t g x + 1 , тогда ее можно рассмотреть в качестве сложной вида g ( x ) = t g x , f ( g ) = g 2 + 3 g + 1 . Очевидно, что необходимо применение формулы для сложной производной:

f ' ( g ( x ) ) = ( g 2 ( x ) + 3 g ( x ) + 1 ) ' = ( g 2 ( x ) ) ' + ( 3 g ( x ) ) ' + 1 ' = = 2 · g 2 - 1 ( x ) + 3 · g ' ( x ) + 0 = 2 g ( x ) + 3 · 1 · g 1 - 1 ( x ) = = 2 g ( x ) + 3 = 2 t g x + 3 ; g ' ( x ) = ( t g x ) ' = 1 cos 2 x ⇒ y ' = ( f ( g ( x ) ) ) ' = f ' ( g ( x ) ) · g ' ( x ) = ( 2 t g x + 3 ) · 1 cos 2 x = 2 t g x + 3 cos 2 x

Функция вида y = t g x 2 + 3 t g x + 1 не считается сложной, так как имеет сумму t g x 2 , 3 t g x и 1 . Однако, t g x 2 считается сложной функцией, то получаем степенную функцию вида g ( x ) = x 2 и f , являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что

y ' = ( t g x 2 + 3 t g x + 1 ) ' = ( t g x 2 ) ' + ( 3 t g x ) ' + 1 ' = = ( t g x 2 ) ' + 3 · ( t g x ) ' + 0 = ( t g x 2 ) ' + 3 cos 2 x

Переходим к нахождению производной сложной функции ( t g x 2 ) ' :

f ' ( g ( x ) ) = ( t g ( g ( x ) ) ) ' = 1 cos 2 g ( x ) = 1 cos 2 ( x 2 ) g ' ( x ) = ( x 2 ) ' = 2 · x 2 - 1 = 2 x ⇒ ( t g x 2 ) ' = f ' ( g ( x ) ) · g ' ( x ) = 2 x cos 2 ( x 2 )

Получаем, что y ' = ( t g x 2 + 3 t g x + 1 ) ' = ( t g x 2 ) ' + 3 cos 2 x = 2 x cos 2 ( x 2 ) + 3 cos 2 x

Функции сложного вида могут быть включены в состав сложных функций, причем сами сложные функции могут являться составными функции сложного вида.

Для примера рассмотрим сложную функцию вида y = log 3 x 2 + 3 cos 3 ( 2 x + 1 ) + 7 e x 2 + 3 3 + ln 2 x · ( x 2 + 1 )

Данная функция может быть представлена в виде y = f ( g ( x ) ) , где значение f является функцией логарифма по основанию 3 , а g ( x ) считается суммой двух функций вида h ( x ) = x 2 + 3 cos 3 ( 2 x + 1 ) + 7 e x 2 + 3 3 и k ( x ) = ln 2 x · ( x 2 + 1 ) . Очевидно, что y = f ( h ( x ) + k ( x ) ) .

Рассмотрим функцию h ( x ) . Это отношение l ( x ) = x 2 + 3 cos 3 ( 2 x + 1 ) + 7 к m ( x ) = e x 2 + 3 3

Имеем, что l ( x ) = x 2 + 3 cos 2 ( 2 x + 1 ) + 7 = n ( x ) + p ( x ) является суммой двух функций n ( x ) = x 2 + 7 и p ( x ) = 3 cos 3 ( 2 x + 1 ) , где p ( x ) = 3 · p 1 ( p 2 ( p 3 ( x ) ) ) является сложной функцией с числовым коэффициентом 3 , а p 1 - функцией возведения в куб, p 2 функцией косинуса, p 3 ( x ) = 2 x + 1 - линейной функцией.

Получили, что m ( x ) = e x 2 + 3 3 = q ( x ) + r ( x ) является суммой двух функций q ( x ) = e x 2 и r ( x ) = 3 3 , где q ( x ) = q 1 ( q 2 ( x ) ) - сложная функция, q 1 - функция с экспонентой, q 2 ( x ) = x 2 - степенная функция.

Отсюда видно, что h ( x ) = l ( x ) m ( x ) = n ( x ) + p ( x ) q ( x ) + r ( x ) = n ( x ) + 3 · p 1 ( p 2 ( p 3 ( x ) ) ) q 1 ( q 2 ( x ) ) + r ( x )

При переходе к выражению вида k ( x ) = ln 2 x · ( x 2 + 1 ) = s ( x ) · t ( x ) видно, что функция представлена в виде сложной s ( x ) = ln 2 x = s 1 ( s 2 ( x ) ) с целой рациональной t ( x ) = x 2 + 1 , где s 1 является функцией возведения в квадрат, а s 2 ( x ) = ln x - логарифмической с основанием е .

Отсюда следует, что выражение примет вид k ( x ) = s ( x ) · t ( x ) = s 1 ( s 2 ( x ) ) · t ( x ) .

Тогда получим, что

y = log 3 x 2 + 3 cos 3 ( 2 x + 1 ) + 7 e x 2 + 3 3 + ln 2 x · ( x 2 + 1 ) = = f n ( x ) + 3 · p 1 ( p 2 ( p 3 ( x ) ) ) q 1 ( q 2 ( x ) ) = r ( x ) + s 1 ( s 2 ( x ) ) · t ( x )

По структурам функции стало явно, как и какие формулы необходимо применять для упрощения выражения при его дифференцировании. Для ознакомления подобных задач и и для понятия их решения необходимо обратиться к пункту дифференцирования функции, то есть нахождения ее производной.

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Конспект урока по теме Сложная функция.docx

Департамент внутренней и кадровой политики Белгородской области

областное государственное автономное образовательное учреждение

среднего профессионального образования

Методическая разработка

открытого урока

Съедина В.В .

Белгород - 2014

Пояснительная записка

Урок разработан для обучающихся 1 курса специальностей среднего профессионального образования, реализующих образовательные программы среднего (полного) общего образования.

Урок рассчитан на 1 академический час (45 минут).

Приложения к конспекту урока;

- индивидуальные карты-модули для учащихся.

Конспект открытого урока по математике

Тип урока – изучение нового материала

создать условия для развития познавательного интереса учащихся, развития аналитического мышления, расширения кругозора учащихся.

создать условия для развития математической культуры, культуры речи, создать условия для воспитания целеустремленности, аккуратности

Целью изучения данной темы является формирование общих и профессиональных компетенций обучающихся:

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 8 Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ПК 6.4 Контролировать ход и оценивать результаты выполнения работ

ПК 6.5 Вести утвержденную учетно – отчетную документацию

Оборудование:

Экран, проектор, доска;

Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2010, Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2009.

Структура урока:

I . Организационный момент - 0,5 мин.

II . Этап подготовки учащихся к активному сознательному усвоению знаний – 4,5 мин.

III . Этап усвоения новых знаний – 30 мин.

IV . Этап закрепления новых знаний – 8 мин.

V . Этап информирования учащихся о домашнем задании и инструктажа по его выполнению - 2 мин.

I . Организационный момент

II . Этап подготовки учащихся к активному сознательному усвоению знаний

Наша с вами задача убедиться, что сложная функция – это не значит трудная!

Прежде чем рассматривать сложную функцию, давайте вспомним основные понятия, которые нам сегодня потребуются при изучении нового материала. Перед каждым из вас лежат индивидуальные карты, прочтите 5 вопросов, которые там приведены, подумайте и ответьте на них. У вас в распоряжении 1,5 мин.

Вводная беседа по ранее изученному материалу:

1. Что значит задать функцию?

2. Что такое аргумент функции?

3. Что такое значение функции?

4. Что называют областью определения функции?

5. Что называют областью значений функции?

Итак, еще раз обращаю ваше внимание, что функция, это прежде всего некоторое соответствие между множеством Х (независимых переменных) и множеством У (значений функции), при этом обязательно нужно помнить что каждому значению х соответствует единственное значение у.

III . Этап усвоения новых знаний

Рассмотреть слайд, обратить внимание на промежуточный шаг x ₀ → t ₀ → y ₀ .

Сложную функцию можно задать формулой y = f ( g ( x )), где g ( x ) – внутренняя функция, f ( t ) – внешняя функция. Обратите внимание, эта формула есть в ваших индивидуальных картах .

Рассмотрим пример сложной функции

g ( x ) = – внутренняя функция, f ( t ) = – внешняя функция.

Найдите y (2)-?

1) Сначала нужно найти значение подкоренного выражения 2 2 -4=0, то есть g ( x ) = x 2 -4 – будет внутренней функцией;

2) затем уже находим значение корня =0, то есть f ( t ) = будет внешней функцией.

Перед вами на экране и в индивидуальных картах приведены примеры сложных функций: y = sin 2 x , y = (x 3 – 1 ) 5 , y = cos (7 x + 2), ,

y = sin 2 x + sin x .

Вам необходимо определить какая функция является внутренней, а какая внешней, и заполнить таблицу. На выполнение задания вам дается 3 минуты.

Помимо умения различать в заданных функциях внутреннюю и внешнюю функции необходимо уметь составлять композицию функций.

На экране приведены три элементарных функции. Вам необходимо составить композицию этих функций по заданным формулам.

Например y = h ( f ( x ))=[ f ( x )= t = x 2 , h ( t )= sin t ] = sin x 2

Рассуждая аналогично, составьте, пожалуйста, композицию из функций в соответствии с заданием, на выполнение этого задания вам дается 3 минуты.

Итак, мы с вами рассмотрели, как в аналитически заданной функции определить внутреннюю и внешнюю функции.

Что бы еще раз убедиться, что сложная функция является композицией двух функций, построим график функции _.

_{Фронтальная беседа (2 мин):}

_{1. Определите внутреннюю и внешнюю функции.}

_{2. Укажите область определения каждой функции}

_{3. Что можно сказать о четности этой функции.}

Как мы уже говорили, сложная функция – это композиция функций. Построим графики внутренней и внешней функции в координатных осях XOG и GO У. Для этого составим таблицы значений каждой функции. Заполните таблицы в индивидуальных картах (2 минуты).

Проверьте правильность своих вычислений, и как показано на экране, постройте графики двух функций в разных системах координат (на построение у вас - 3 минуты).

Посмотрите на экран, вот что у вас должно было получиться.

А теперь рассмотрим как, используя полученные графики, построить график сложной функции.

Возьмем некоторое х ₀ =0 и по первому графику найдем соответствующее ему значение g ₀ =-1, затем по второму графику для g ₀ =-1, найдем у ₀ =1/2 и построим в новой системе координат точку с координатами (0:1/2). Аналогично, можно построить и другие точки x ₁ =1 → g ₁ =0 → y ₁ =1→(1;1), учитывая четность функции, получаем точку (-1;1). И строим эскиз графика сложной функции.

Проделайте эту операцию самостоятельно в своих индивидуальных картах, для удобства можете использовать вспомогательную таблицу. На выполнение работы 5 мин. (пройти для проверки и корректировки выполнения задания, проверить выполнение заданий по определению внутренней и внешней функции, составлению сложных функций).

IV . Этап закрепления новых знаний

Используя имеющиеся графики, постройте график функции y =(2 x ) 2 -1

(на выполнение 4 минуты) – первый справившийся учащийся на доске выполняет чертеж графика

Итак, мы рассмотрели понятие сложной функции как композицию двух функций, внешней и внутренней. Научились распознавать эти функции в конкретно заданной функции, а также составлять композицию двух функций. А также посмотрели, как с помощью графиков элементарных функций можно построить график сложной функции.

2. Как распознать внешнюю и внутреннюю функции?

3. Можно ли утверждать, что график сложной функции - это обязательно сложная кривая, для построения которой необходимы сложные вычисления и преобразования?

По итогам работы на уроке выставляются отметки активным учащимся.

V . Этап информирования учащихся о домашнем задании и инструктажа по его выполнению

В ваших индивидуальных картах записано домашнее задание: построить график функции

Читайте также: