Персептрон своими руками
Обновлено: 06.07.2024
На предыдущем занятии мы с вами увидели как работает полносвязная НС со ступенчатой активационной функцией:
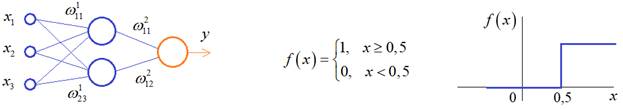

Такими были первые нейронные сети, предложенные Френком Розенблаттом в 1957 году. Давайте посмотрим, какие возможности дает нам такая нейросетевая архитектура. И для простоты рассмотрим простейший персептрон для задачи классификации двух классов образов, представленных двумя характеристиками: :

С активационной функцией:

То есть, если значение суммы больше или равно 0, то вектор принадлежит классу 1:



Это может быть разделение на кошек и собак, на мужчин и женщин, на наличие сигнала и его отсутствие и т.п. Мы здесь обобщаем все эти случаи и представляем их в виде двух классов: .
Далее, из вида активационной функции видно, что граница разделения двух классов проходит на уровне 0. То есть, если:


определяет границу разделения одного класса образов от другого. Ее еще можно записать в виде:

То есть, это прямая с угловым коэффициентом

проходящая через начало системы координат:

И все точки по одну сторону от этой прямой будут относиться к одному классу, а по другую сторону – к другому классу. Такая прямая получила название разделяющей прямой. (В многомерном случае она превращается в гиперплоскость и называется разделяющей гиперплоскостью). Этот двумерный график хорошо демонстрирует возможность правильной классификации простейшим персептроном только линейно-разделимых образов.
Чтобы все было понятнее, давайте в качестве примера смоделируем в Python два класса линейно-разделимых образов разделяющей прямой:

то есть, прямой, идущей под 45 градусов к осям координат. В этом случае, для корректной классификации, мы должны выбрать веса нейронной сети равными, но с противоположными знаками:

Я здесь взял коэффициенты по 0,3 с противоположным знаком. Можно выбрать и любые другие, например, -1 и 1 и т.п. И, как видим, наша НС успешно классифицирует эти образы. Но, если коэффициенты взять не равными, например:

то первый класс будет неверно распознаваться. Это, в частности, означает, что НС неверно настроена на классификацию таких образов и ее весовые коэффициенты нуждаются в корректировке.
Вернем все к рабочему состоянию с весами:


И предположим, что все наши образы сдвигаются вверх по оси :

Теперь, наша разделяющая прямая не сможет верно классифицировать такие образы, т.к. она проходит через начало координат. И как бы мы ее ни крутили, корректного разделения не получится. Необходимо смещение. Поэтому, в НС дополнительно определяют еще один вход для смещения разделяющей гиперплоскости. В английской литературе он называется bias (перевести можно как порог).

С этим дополнительным входом, наша прямая принимает вид:

то есть, мы можем теперь сдвинуть ее на любое требуемое значение.

Давайте предположим, что все образы сдвинуты вверх по оси на величину b. Тогда третий весовой коэффициент НС следует выбрать из уравнения:

Определяем все это в нашей программе, добавляем к входному вектору третье значение +1 и теперь наша НС корректно классифицирует такие смещенные образы.
Теперь вы знаете, зачем нужен биас в НС. Это смещение используется во всех современных сетях, а не только в персептроне. Здесь я лишь показал пример необходимости его использования. Но та же самая картина сохраняется и для других видов НС с большими размерностями.
Задача XOR
Рассмотренная нами НС с одним нейроном, может классифицировать только линейно-разделимые образы. Однако, на практике чаще встречаются более сложные задачи. Например, представим, что классы наших образов распределены следующим образом:

Здесь невозможно провести одну линию для их правильной классификации. Как тогда быть? Например, провести две линии, вот так:

И все, что будет попадать между ними – отнесем к первому классу, а за их пределами – ко второму классу. Что это за НС, которая способна на такие операции? В действительности, все просто: каждая разделительная линия может быть представлена отдельным нейроном, а затем, результат их классификации объединяется результирующим нейроном выходного слоя:

Давайте, для простоты, будем полагать, что на входы подаются только значения 0 или 1:

Тогда, все наши образы будут лежать в углах квадрата:


Смотрите, если , то получаем таблицу истинности для битовой операции XOR (исключающее ИЛИ). Поэтому в литературе задача разделения таких образов получила название задачи XOR.
Далее, активационная функция каждого нейрона будет иметь вид:

Осталось определить веса связей НС для решения поставленной задачи классификации. Для начала, положим, что первый нейрон скрытого слоя будет формировать границу:

Учитывая, нашу формулу:


Веса входов первого нейрона для можно взять равными:

а вес третьей связи:

Все, получили прямую, которая формирует следующее разделение на плоскости:

Второй нейрон скрытого слоя будет формировать разделения прямой:

и веса его связей можно взять равными:
и
Получаем следующую картину:

Теперь, нам нужно объединить результаты их работы, чтобы получилась следующая разделяющая область:

Как это сделать? То есть, как выбрать веса для выходного нейрона, чтобы получить такую картину классификации? Если результаты просто сложить, то получим разделение вида и на выходе активационной функции увидим одну большую область с 1 и одну область с 0.
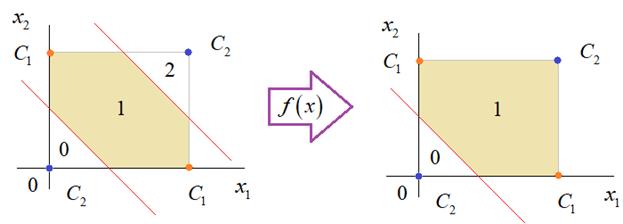
Это не годится. Лучше из второго вычесть первое:
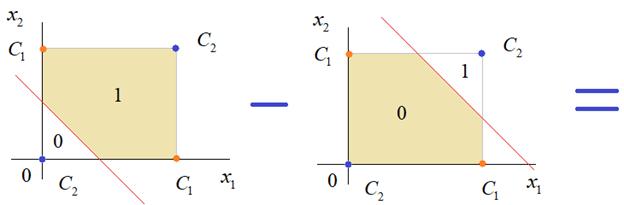
И на входе выходного нейрона будем получать значения:

Для надежности сместим эти значения на -0,5 и окончательно получим результат:

То есть, веса в нашей НС, будут следующими:

На Python эту НС можно реализовать следующим образом. Как видим, результаты получаются именно такими, какие мы и ожидали, классификация задачи XOR выполнена успешно благодаря добавлению скрытого слоя нейронов.
Этот пример хорошо показывает, что добавляя новые нейроны, мы можем получать все более сложные формы разделяющих выпуклых областей, полученные комбинацией разделяющих линий или гиперплоскостей. Это приводит к более сложным схемам классификации, уходящей далеко за пределы линейно-разделимых образов.
Видео по теме

Нейронные сети: краткая история триумфа
































© 2022 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта

Персептрон – это нейронная сеть, которая представляет собой алгоритм для выполнения двоичной классификации. Он определяет, относится ли объект к определенной категории (например, является ли животное на рисунке кошкой или нет).
Персептрон занимает особое место в истории нейронных сетей и искусственного интеллекта, потому что первоначальные иллюзии по поводу его эффективности привели к появлению т. н. опровержения Минского-Паперта и застою в исследованиях нейронных сетей, который продлился несколько десятилетий. Лед тронулся после публикации работ Джеффа Хинтона в 2000-х годах, результаты которого преобразили все области машинного обучения.

Фрэнк Розенблатт

Персептрон представляет собой линейный классификатор, то есть алгоритм, который классифицирует объект путем разделения двух категорий прямой. Объектом обычно является вектор-функция x, взятая с весом w и смещенная на b: y = w * x + b.
На выходе персептрон выдает результат y, основанный на нескольких вещественных входных объектах путем формирования линейной комбинации с использованием весовых коэффициентов (иногда с последующим пропусканием результата через нелинейную функцию активации). Вот как это выглядит на языке математики:

где w – вектор весовых коэффициентов, x – вектор входных объектов, b – смещение, φ – функция нелинейной активации.

Многослойный персептрон
Последующее исследование многослойных персептронов показало, что они способны аппроксимировать как оператор XOR, так и многие другие нелинейные функции.
Так же, как Розенблатт основал персептрон на нейроне Маккаллоха-Питса, разработанном в 1943 году, так и сами персептроны являются строительными блоками, которые могут быть полезны только в таких больших функциях, как многослойные персептроны.
Многослойный персептрон — это хорошая стартовая точка для изучения глубокого обучения.
Многослойный персептрон представляет собой глубокую искусственную нейронную сеть, включающую в себя несколько персептронов. Многослойные персептроны состоят из входного слоя для приема сигнала, выходного слоя, который принимает решение или делает предсказание о входном объекте, а между ними – произвольное количество скрытых слоев, которые являются истинным вычислительным движком. Многослойные персептроны с одним скрытым слоем способны аппроксимировать любую непрерывную функцию.
Как работает персептрон
Персептроны часто применяются для решения контролируемых задач обучения: они тренируются по набору пар входных/выходных объектов и учатся моделировать корреляции (т. е. зависимости) между этими данными. Обучение включает в себя настройку параметров модели (весовых коэффициентов, смещений) для минимизации погрешности. Для корректировки этих параметров относительно погрешности используется алгоритм обратного распространения, а сама погрешность может быть вычислена различными способами, в том числе путем вычисления среднеквадратичного отклонения (RMSE).
Сети прямого распространения, такие как многослойный персептрон, похожи на теннис или пинг-понг. Они в основном состоят из двух видов движений: вперед и назад. Получается своеобразная игра в пинг-понг между догадками и ответами, поскольку каждая догадка – это проверка того, что мы знаем, а каждый ответ – это обратная связь, позволяющая нам узнать, насколько сильно мы ошибаемся.
При шаге вперед поток сигнала перемещается от входного слоя через скрытые к выходному, а решение, полученное на выходном слое, сравнивается с априорно известным верным ответом.
При шаге назад с использованием правила дифференцирования сложных функций через персептрон в обратном направлении распространяются частные производные функции, погрешности по весовым коэффициентам и смещениям. Данный акт дифференцирования дает нам градиент погрешности, с использованием которого могут быть скорректированы параметры модели, так как они приближают МП на один шаг ближе к минимуму погрешности. Это можно сделать с помощью любого алгоритма градиентной оптимизации, например, методом стохастического градиентного спуска. Сеть продолжает играть в пинг-понг, пока погрешность не исчезнет. В этом случае, как говорят, наступает сходимость.
Совершенствование персептрона
Дальнейшее изучение вопроса может привести вас к потребности разработки все более и более сложных и полезных алгоритмов. Мы переходим от одного нейрона к совокупности нескольких, называемой слоем; затем переходим от одного слоя к совокупности нескольких, называемой многослойным персептроном. Можем ли мы перейти от одного МП к нескольким, или же мы просто будем дальше нагромождать слои, как это сделала Microsoft со своим лидером ImageNet, ResNet, в котором было более 150 слоев? Или же правильным является комбинирование МП – ансамбля многих алгоритмов, голосующих в своего рода вычислительной демократии за лучший прогноз? Или это по сути лишь встраивание одного алгоритма в другой, как это происходит со сверточными графовыми сетями?
Рассмотрим наиболее простые модели нейронных сетей : однослойный и многослойный персептрон .
Персептрон
Большое количество моделей персептрона рассмотрено в основополагающей работе Розенблатта [47]. Простейшая модель нейронной сети - однослойный персептрон .
Однослойный персептрон (персептрон Розенблатта) - однослойная нейронная сеть , все нейроны которой имеют жесткую пороговую функцию активации.
Однослойный персептрон имеет простой алгоритм обучения и способен решать лишь самые простые задачи. Эта модель вызвала к себе большой интерес в начале 1960-х годов и стала толчком к развитию искусственных нейронных сетей .
Классический пример такой нейронной сети - однослойный трехнейронный персептрон - представлен на рис. 11.3.

Сеть, изображенная на рисунке, имеет n входов, на которые поступают сигналы, идущие по синапсам на 3 нейрона. Эти три нейрона образуют единственный слой данной сети и выдают три выходных сигнала.
Многослойный персептрон ( MLP ) - нейронная сеть прямого распространения сигнала (без обратных связей), в которой входной сигнал преобразуется в выходной, проходя последовательно через несколько слоев .
Первый из таких слоев называют входным, последний - выходным. Эти слои содержат так называемые вырожденные нейроны и иногда в количестве слоев не учитываются. Кроме входного и выходного слоев , в многослойном персептроне есть один или несколько промежуточных слоев , которые называют скрытыми.
В этой модели персептрона должен быть хотя бы один скрытый слой . Присутствие нескольких таких слоев оправдано лишь в случае использования нелинейных функций активации .
Пример двухслойного персептрона представлен на рис. 11.4.

Сеть, изображенная на рисунке, имеет n входов. На них поступают сигналы, идущие далее по синапсам на 3 нейрона, которые образуют первый слой . Выходные сигналы первого слоя передаются двум нейронам второго слоя . Последние, в свою очередь, выдают два выходных сигнала.
Метод обратного распространения ошибки (Back propagation , backprop) - алгоритм обучения многослойных персептронов , основанный на вычислении градиента функции ошибок . В процессе обучения веса нейронов каждого слоя нейросети корректируются с учетом сигналов, поступивших с предыдущего слоя , и невязки каждого слоя , которая вычисляется рекурсивно в обратном направлении от последнего слоя к первому.
Эта реализация не предназначена для крупномасштабных приложений. В частности, scikit-learn не поддерживает GPU. Чтобы узнать о гораздо более быстрых реализациях на базе графического процессора, а также о фреймворках, предлагающих гораздо большую гибкость для создания архитектур глубокого обучения, см. Связанные проекты .
1.17.1. Многослойный персептрон
Многослойный персептрон (MLP) — это алгоритм обучения с учителем, который изучает функцию $f(\cdot): R^m \rightarrow R^o$ обучением на наборе данных, где m — количество измерений для ввода и o- количество размеров для вывода. Учитывая набор функций $X = $ и цель $y$, он может изучить аппроксиматор нелинейной функции для классификации или регрессии. Он отличается от логистической регрессии тем, что между входным и выходным слоями может быть один или несколько нелинейных слоев, называемых скрытыми слоями. На рисунке 1 показан MLP с одним скрытым слоем со скалярным выходом.

Рисунок 1: Один скрытый слой MLP.
Самый левый слой, известный как входной, состоит из набора нейронов $$ представляющие входные функции. Каждый нейрон в скрытом слое преобразует значения из предыдущего слоя с взвешенным линейным суммированием $w_1x_1 + w_2x_2 + … + w_mx_m$, за которой следует нелинейная функция активации $g(\cdot):R \rightarrow R$ — как функция гиперболического загара. Выходной слой получает значения из последнего скрытого слоя и преобразует их в выходные значения.
Модуль содержит публичные атрибуты coefs_ и intercepts_ . coefs_ список весовых матриц, где весовая матрица с индексомi представляет собой веса между слоями i и слой $i+1$. intercepts_ список векторов смещения, где вектор с индексом $i$ представляет значения смещения, добавленные к слою $i+1$.
Преимущества многослойного перцептрона:
- Возможность изучать нелинейные модели.
- Возможность изучения моделей в режиме реального времени (онлайн-обучение) с использованием partial_fit .
К недостаткам многослойного персептрона (MLP) можно отнести:
- MLP со скрытыми слоями имеют невыпуклую функцию потерь, когда существует более одного локального минимума. Поэтому разные инициализации случайных весов могут привести к разной точности проверки.
- MLP требует настройки ряда гиперпараметров, таких как количество скрытых нейронов, слоев и итераций.
- MLP чувствителен к масштабированию функций.
1.17.2. Классификация
Класс MLPClassifier реализует алгоритм многослойного перцептрона (MLP), который обучается с использованием обратного распространения .
MLP обучается на двух массивах: массив X размера (n_samples, n_features), который содержит обучающие образцы, представленные как векторы признаков с плавающей запятой; и массив y размера (n_samples,), который содержит целевые значения (метки классов) для обучающих выборок:
После подгонки (обучения) модель может предсказывать метки для новых образцов:
MLP может подгонять нелинейную модель к обучающим данным. clf.coefs_ содержит весовые матрицы, составляющие параметры модели:
В настоящее время MLPClassifier поддерживает только функцию потерь кросс-энтропии, которая позволяет оценивать вероятность путем запуска predict_proba метода.
MLP тренирует с использованием обратного распространения ошибки. Точнее, он тренируется с использованием некоторой формы градиентного спуска, а градиенты вычисляются с использованием обратного распространения. Для классификации он минимизирует функцию потерь кросс-энтропии, давая вектор оценок вероятности $P(y|x)$ за образец $x$:
MLPClassifier поддерживает мультиклассовую классификацию, применяя Softmax в качестве выходной функции.
Кроме того, модель поддерживает классификацию с несколькими метками, в которой образец может принадлежать более чем одному классу. Для каждого класса необработанные выходные данные проходят через логистическую функцию. Значения, большие или равные 0.5 , округляются до 1 , в противном случае — до 0 . Для прогнозируемых выходных данных выборки индексы, в которых указано значение, 1 представляют назначенные классы этой выборки:
См. Примеры ниже и строку документации MLPClassifier.fit для получения дополнительной информации.
1.17.3. Регрессия
Класс MLPRegressor реализует многослойный перцептрон (MLP), который обучается с использованием обратного распространения без функции активации в выходном слое, что также можно рассматривать как использование функции идентификации в качестве функции активации. Следовательно, он использует квадратную ошибку как функцию потерь, а на выходе представляет собой набор непрерывных значений.
MLPRegressor также поддерживает регрессию с несколькими выходами, при которой в выборке может быть более одной цели.
1.17.4. Регуляризация
Оба MLPRegressor и MLPClassifier используют параметр alpha для термина регуляризации (L2-регуляризация), который помогает избежать переобучения, штрафуя веса большими величинами. Следующий график отображает изменяющуюся функцию решения со значением альфа.
См. Примеры ниже для получения дополнительной информации.
1.17.5. Алгоритмы
MLP тренирует с использованием стохастического градиентного спуска , Адама или L-BFGS . Стохастический градиентный спуск (SGD) обновляет параметры, используя градиент функции потерь по отношению к параметру, который требует адаптации, т. Е.
$$w \leftarrow w — \eta (\alpha \frac<\partial R(w)> <\partial w>+ \frac<\partial Loss><\partial w>)$$
где $\eta$ — это скорость обучения, которая контролирует размер шага при поиске в пространстве параметров. $Loss$ — функция потерь, используемая для сети.
Более подробную информацию можно найти в документации SGD.
Adam похож на SGD в том смысле, что это стохастический оптимизатор, но он может автоматически регулировать количество для обновления параметров на основе адаптивных оценок моментов более низкого порядка.
С SGD или Adam обучение поддерживает онлайн и мини-пакетное обучение.
L-BFGS — это решающая программа, которая аппроксимирует матрицу Гессе, которая представляет собой частную производную второго порядка функции. Кроме того, он аппроксимирует обратную матрицу Гессе для обновления параметров. Реализация использует версию L-BFGS Scipy .
1.17.6. Сложность
Предположим, есть $n$ обучающие образцы, $m$ Особенности, $k$ скрытые слои, каждый из которых содержит $h$ нейроны — для простоты и $o$ выходные нейроны. Временная сложность обратного распространения ошибки равна $O(n\cdot m \cdot h^k \cdot o \cdot i)$, где $i$- количество итераций. Поскольку обратное распространение имеет высокую временную сложность, рекомендуется начинать с меньшего количества скрытых нейронов и нескольких скрытых слоев для обучения.
1.17.7. Математическая постановка
Учитывая набор обучающих примеров $(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)$ где $x_i \in \mathbf^n$ а также $y_i \in $, один скрытый слой один скрытый нейрон MLP изучает функцию $f(x) = W_2 g(W_1^T x + b_1) + b_2$ где $W_1 \in \mathbf^m$ а также $W_2, b_1, b_2 \in \mathbf$ параметры модели. $W_1, W_2$ представляют веса входного слоя и скрытого слоя соответственно; а также $b_1, b_2$ представляют смещение, добавленное к скрытому слою и выходному слою соответственно. $g(\cdot) : R \rightarrow R$- функция активации, установленная по умолчанию как гиперболический загар. Это дается как,
$$g(z)= \frac>>$$
Для бинарной классификации $f(x)$ проходит через логистическую функцию $g(z)=1/(1+e^)$ для получения выходных значений от нуля до единицы. Порог, установленный на 0,5, будет назначать образцы выходных данных, превышающих или равных 0,5, положительному классу, а остальные — отрицательному классу.
Если классов больше двух, $f(x)$ сам был бы вектором размера (n_classes,). Вместо того, чтобы проходить через логистическую функцию, он проходит через функцию softmax, которая записывается как,
$$\text(z)i = \frac^k\exp(z_l)>$$
где $z_i$ представляет $i$-тый элемент ввода в softmax, который соответствует классу $i$, а также $K$ количество классов. Результатом является вектор, содержащий вероятности, которые выбирают $x$ принадлежат к каждому классу. На выходе получается класс с наибольшей вероятностью.
В регрессии результат остается как $f(x)$; следовательно, функция активации выхода — это просто функция идентичности.
MLP использует разные функции потерь в зависимости от типа проблемы. Функция потерь для классификации — это кросс-энтропия, которая в двоичном случае задается как,
$$Loss(\hat,y,W) = -y \ln <\hat> — (1-y) \ln<(1-\hat)> + \alpha ||W||_2^2$$
где $\alpha ||W||_2^2$ это термин L2-регуляризации (также известный как штраф), который штрафует сложные модели; а также $\alpha > 0$ неотрицательный гиперпараметр, определяющий величину штрафа.
Для регрессии MLP использует функцию потерь квадратичной ошибки; написано как,
$$Loss(\hat,y,W) = \frac||\hat — y ||_2^2 + \frac ||W||_2^2$$
Начиная с начальных случайных весов, многослойный персептрон (MLP) минимизирует функцию потерь, многократно обновляя эти веса. После вычисления потерь при обратном проходе они распространяются с выходного уровня на предыдущие уровни, предоставляя каждому параметру веса значение обновления, предназначенное для уменьшения потерь.
При градиентном спуске градиент $\nabla Loss_$ потери по весам вычисляется и вычитается из $W$. Более формально это выражается как,
$$W^ = W^i — \epsilon \nabla _^$$
где $i$ — шаг итерации, а ϵ скорость обучения со значением больше 0.
Алгоритм останавливается, когда достигает заданного максимального количества итераций; или когда улучшение потерь ниже определенного небольшого числа.
1.17.8. Советы по практическому использованию
- Многослойный персептрон чувствителен к масштабированию функций, поэтому настоятельно рекомендуется масштабировать ваши данные. Например, масштабируйте каждый атрибут во входном векторе X до [0, 1] или [-1, +1] или стандартизируйте его, чтобы он имел среднее значение 0 и дисперсию 1. Обратите внимание, что вы должны применить такое же масштабирование к набору тестов для значимые результаты. Можно использовать StandardScaler для стандартизации.
- Альтернативный и рекомендуемый подход — использовать StandardScaler в Pipeline
- Нахождение разумного параметра регуляризации $\alpha$ лучше всего использовать GridSearchCV , обычно в диапазоне 10.0 ** -np.arange(1, 7)
- Эмпирическим L-BFGS путем мы заметили, что это происходит быстрее и с лучшими решениями на небольших наборах данных. Однако для относительно больших наборов данных Adam это очень надежно. Обычно он быстро сходится и дает довольно хорошую производительность. SGD с импульсом или импульсом нестерова, с другой стороны, может работать лучше, чем эти два алгоритма, если скорость обучения настроена правильно.
1.17.9. Больше контроля с warm_start
Если вы хотите получить больше контроля над критериев остановки или скорости обучения в СГД, или хотите сделать дополнительный мониторинг, используя warm_start=True и max_iter=1 и переборе сами могут быть полезны:
Читайте также:

