Как сделать чередование знаков в с
Обновлено: 08.07.2024
Репутация: нет
Всего: нет
Хочу изучить язык Паскаль по книжке, самостоятельно.И у меня возник вопрос.
Не могу решить вот эту задачу:
Определить сколько раз последовательность из N произвольных чисел меняет знак.
Просто не знаю, что делать с этими произвольными числами . Может есть какой-нибудь оператор Паскаля, который занимается этим делом.
Желательно бы и алгоритм к этой задаче.Весь его писать не надо просто объясните, как решать вопрос с произвольными числами.
| M Kuvaldis | 1. Название темы должно отражать ее суть 2. Не забываем указывать в заголовке темы нужный язык программирования |
Репутация: 11
Всего: 360
Для домашних заданий, курсовых, существует "Центр Помощи"
Репутация: 12
Всего: 24
| Цитата(Sven777 @ 2.7.2007, 19:02 ) |
| Просто не знаю, что делать с этими произвольными числами |
так в чем проблема то? если нужно получить произвольные числа, можешь просто ввести их с клавиатуры. главное в этой задаче - алгоритм определения чилса смен знакак.
Репутация: нет
Всего: нет
Репутация: 12
Всего: 24
есть и генератор: random(N) - случайное число от 1 до N. (вначале программы нужно вызвать процедуру randomize; для инициализации генератора случайных чисел)
но в данном случае (как я понял) это не важно, главное - придумать алгоритм посчета числа смен знаков.
Репутация: нет
Всего: нет
Репутация: 12
Всего: 24
просто в начале программы один раз вызываешь randomize; для инициализации генератора
затем для получения случайного числа (от 1 до N) вызываешь random(N);
Репутация: нет
Всего: нет
likehood, Спасибо
Репутация: 32
Всего: 61
Sven777,
Тебе нужно сгенерировать случайное число так, чтобы оно могло быть как положительное, так и отрицательное.
random(N) генерит случайное число из интервала (1, N)
Поэтому используй для заполнения такую формулу:
переменная = Random(1, N) - N/2
Тогда значение будет между (-N/2, N/2)
Репутация: нет
Всего: нет
| Код |
Const MSize =100; var Mas : array[1..MSize] of integer; i : Integer; Count : integer; создаешь массив с произвольными числами randomize; for i:=1 to MSize do Mas[i] :=random(100)-50; // как предложил Kuvaldis Count :=0; for i:=2 to MSize do if Sign(Mas[i-1])*Sign(Mas[i]) = -1 then Inc(Count); // сделать проверку на 0 writeln('кол-во изменений '+ IntToStr(Count)); // или ф-ция Str если Pascal |
Репутация: нет
Всего: нет
Задачу вроде бы решил.Произвольные числа вводяться с клавиатуры.
//Произведение двух чисел с разными знаками - отрицательное число//
На это и опирался.Немного топорно, конечно, получилось, но ничего задача работает правильно! Как на ваш взгляд все правильно сделал или можно было бы как-нибудь упростить, а то громозко как-то выглядит?
| Код |
Program upr5; uses crt; var x0,x1,n,i,k:integer; Begin clrscr; write('n='); readln(n); write('x0='); readln(x0); write('x1='); readln(x1); k:=0; i:=1; while i =n then break; x0:=x1; write('x1='); readln(x1); end; writeln('k=',k); readkey; End. |
| M Kuvaldis | Не забываем пользоваться тегами для подсветки кода |
Репутация: 12
Всего: 24
Прежде всего бросаются в глаза строчки 19 и 21, в которых происходит одно и то же действие в разных частях условного оператора. Поскольку увеличить i нужно в любом случае, лучше сделать это после условного оператора. Кстати, в данном случае лучше было использовать цикл for, тогда i увеличивалось бы автоматически.
Еще я бы перенёс ввод x1 в начало цикла, тогда в начале программы не нужно было бы вводить x1 и, кроме того, можно было бы убрать условие в 22 строке.
Ну и еще не помешает сделать нормальные отступы, чтобы программу было проще читать.
Репутация: нет
Всего: нет
| Цитата |
Еще я бы перенёс ввод x1 в начало цикла, тогда в начале программы не нужно было бы вводить x1 и, кроме того, можно было бы убрать условие в 22 строке. |
Вот эта идея мне понравилась. Учту эти замечания и попытаюсь переделать программу.
| Цитата |
Ну и еще не помешает сделать нормальные отступы, чтобы программу было проще читать. |
Репутация: 12
Всего: 24
| Цитата(Sven777 @ 3.7.2007, 21:16 ) |
| А как надо правильно делать эти отступы. |
| Код |
Program upr5; uses crt; var x0,x1,n,i,k:integer; Begin clrscr; write('n='); readln(n); write('x0='); readln(x0); write('x1='); readln(x1); k:=0; i:=1; while i =n then break; x0:=x1; write('x1='); readln(x1); end; writeln('k=',k); readkey; End. |
После каждого begin'а делатеся отступ (обычно 4 пробела).
Репутация: нет
Всего: нет
Если Вам помогли и атмосфера форума Вам понравилась, то заходите к нам чаще! С уважением, Poseidon, Rodman
[ Время генерации скрипта: 0.1470 ] [ Использовано запросов: 21 ] [ GZIP включён ]
Поэтому не ленимся – ТЕРПЕЛИВО рассматриваем КАЖДЫЙ интервал: из КАЖДОГО интервала берём наиболее выгодную точку и выясняем знак функции в данной точке.
Вот простой пример, когда интервала два, но знакочередования нет: . Экспонента всегда положительна , квадрат неотрицателен , поэтому вся функция неотрицательна: , очевидно, достигая нуля в единственной точке . Такого решения будет вполне достаточно. Не обязательно чертить координатную ось! Обратите внимание, здесь есть тонкость при записи ответа:
, если .
То есть, функция положительна везде, кроме точки ноль.

Но формально можно использовать метод интервалов, который приведёт нас к такому же результату:
Если честно, не помню, как выглядит чертёж, однако совершенно точно можно сказать, что график данной функции лежит в верхней полуплоскости и касается оси абсцисс в точке .
Или парабола, касающаяся оси, например: . Такая же история. Кстати, если вы внимательно изучили геометрические преобразования графиков, то сразу поймёте, как расположена данная парабола.
Следует отметить, что ситуация касания графика оси не единственна, в ряде случаев функция не меняет знак при переходе через точку разрыва. Хороший пример встретился в статье Непрерывность функции: .
Найти интервалы знакопостоянства функции.
Функции с многочленами встречаются очень часто, поэтому имеет смысл рассмотреть ещё пару экземпляров:
Найти интервалы знакопостоянства функции.
Решение:
1) Функция определена на всей числовой прямой.
2) Находим нули функции:
Таким образом, нули функции: .

3) Откладываем данные значения на оси абсцисс:
Определим знаки функции на полученных интервалах:

Таким образом:
Ответ:
, если ;
, если .
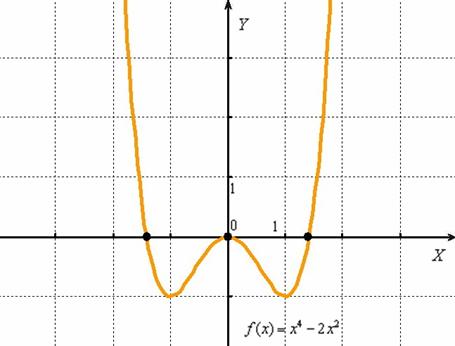
Многочлен 4-ой степени тоже достоин полного графика:
Собрат для самостоятельного решения:
Найти интервалы знакопостоянства функции.
В ходе выполнения задания потребуется решить так называемое биквадратное уравнение, которое также рассматривается в школьном курсе математики. В данном примере необходимо провести замену , разобраться с уравнением , найти корни и на финише из равенств получить 4 корня. Полное решение и ответ в конце урока.
Перейдём к обширной группе функций, у которых есть точки разрыва:
Найти интервалы знакопостоянства функции.
Решение: вот здесь начинает в полную силу работать пункт №1 алгоритма:
1) Функция определена на всей числовой прямой, кроме точки , которая обращает знаменатель в ноль.
2) Находим точки пресечения графика с осью (нули функции):
Знаменатель нулевым быть не может, поэтому приравниваем к нулю числитель и решаем уравнение счастливого первоклассника:

3) Откладываем на оси абсцисс ВСЕ найденные точки, при этом выкалываем точку , так как она не входит в область определения функции:
Определим знаки функции на полученных интервалах:

В результате:
Ответ:
, если ;
, если .
Чем отличается данный пример от всех предыдущих? Да ничем особенным.
Напоминаю, что практически так же решается ряд смежных задач, например:
Решить неравенство
Ответ:
Решить неравенство
Ответ:
Найти область определения функции
Ответ:
Короткое разминочное задание для самостоятельного решения:
Найти интервалы знакопостоянства функции.
Рассмотрим более навороченные дробно-рациональные функции:
Найти интервалы знакопостоянства функции.
Решение: далее пункты алгоритма нумеровать не будем.
Находим область определения функции. Проверим, обращается ли знаменатель в ноль:
Перепишем квадратное уравнение в привычном виде:
И для удобства сменим знаки у каждого слагаемого:
Дискриминант больше нуля, значит, уравнение имеет два действительных корня и в область определения не войдут две точки:
Найдём точки пересечения графика с осью абсцисс: . Нулевым может быть только числитель, поэтому рассматриваем уравнение . Решение можно провести через дискриминант, однако нетрудно заметить, что у нас квадрат разности:
Таким образом, функция обращается в ноль в единственной точке:

Используя уже наработанный алгоритм, определим знаки функции на полученных интервалах:
Ответ:
, если ;
, если .
Как выглядит график функции, знают немногие, но совершенно точно можно сказать, что на интервалах он расположен ВЫШЕ оси , а на интервалах – НИЖЕ данной оси. В точке график, кстати, только касается её.
Найти интервалы знакопостоянства функции.
Это пример для самостоятельного решения.
Заключительные примеры посвящены функциям, в которые входит натуральный логарифм:
Найти интервалы знакопостоянства функции.
Просто и со вкусом.
Решение: функция определена и непрерывна на интервале . Найдём точки пересечения графика с осью абсцисс:
Нулю может быть равен только числитель:
Согласно определению логарифма (которое нужно бы уже хорошо усвоить):

Отметим найденные точки на числовой прямой:
На промежутке функция не определена вообще. Об этом можно сделать пометку на чертеже либо просто оставить полуинтервал без внимания. Я обычно не ставлю никаких знаков.
Определим знаки на интервалах, которые входят в область определения функции:

Таким образом:
Ответ:
, если ;
, если .
На практике под логарифмом часто находится квадратный дву- или трёхчлен. Пожалуйста, ВНИМАТЕЛЬНО изучите оставшиеся примеры, в которых метод интервалов используется ДВАЖДЫ: первый раз для нахождения области определения, а второй раз для нахождения интервалов знакопостоянства.
Найти интервалы знакопостоянства функции.
Решение: сначала найдём область определения функции. Выражение под знаком логарифма должно быть положительным:
Квадратичное неравенство решим методом интервалов. Проверим, существуют ли действительные корни соответствующего уравнения:
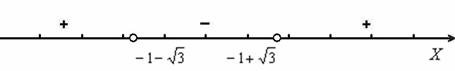
Откладываем найденные точки на числовой прямой. Их следует выколоть, поскольку неравенство строгое. Далее стандартно из каждого интервала выбираем наиболее простую точку, и определяем знаки функции на полученных интервалах:
Таким образом, область определения:
Что теперь? Теперь ЗАБЫВАЕМ про найденные знаки и интервалы знакопостоянства. Самый важный факт состоит в том, что отрезок не входит в область определения функции .
На втором шаге находим точки пересечения графика с осью абсцисс (нули функции):
Решаем ещё одно квадратное уравнение:
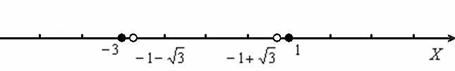
Снова используем метод интервалов. Откладываем на числовой прямой ВСЕ найдённые ранее точки:
Тесновато получилось, но что делать, зато масштаб выдержан.
Определяем знаки функции на интервалах, при этом не забываем, что отрезок посередине не входит в область определения, и возиться с ним не надо! Но от этого, увы, не легче, так как подстановка будет брутальной. Придётся тыкать по клавишам калькулятора:
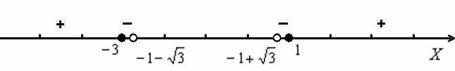
Таким образом:
Ответ:
, если ;
, если .
Что можно сказать о графике функции ? На отрезке его не существует вообще, на крайних интервалах он расположен выше оси , на маленьких интервалах – ниже данной оси, точки пересечения с осью: .
Найти интервалы знакопостоянства функции.
Это пример для самостоятельного изучения. На первом шаге решение можно ускорить – неравенство значительно выгоднее решить аналитически, нежели использовать метод интервалов. Данный способ подробно рассмотрен на уроке Область определения функции.
Вот, пожалуй, и все основные задания по теме, которые встречаются на практике в ходеполного исследования функции. Хочется привести примеры сложнее, но они будут в известной степени надуманы.
Решения и ответы:

Пример 3:Решение:
1) Функция определена на всей числовой прямой.
2) Найдём нули функции:
Таким образом: .
3) Определим знаки функции методом интервалов:
Ответ:
, если ;
, если .

Пример 5:Решение:
1) Функция определена на всей числовой прямой
2) Найдём нули функции:
Проведём замену:
3) Выполним чертёж и определим знаки функции на найденных интервалах:
Ответ:
, если ;
, если .

Пример 7:Решение:
1) Функция определена на всей числовой прямой, кроме точки .
2) Найдём нули функции:
3) Определим знаки функции на полученных интервалах:
Ответ:
, если ;
, если .

Пример 9:Решение: точки не входят в область определения функции.
График функции не пересекает ось , т.к.
Методом интервалов определим знаки функции:
Ответ:
, если ;
, если .

Пример 12:Решение: найдём область определения:
Таким образом,
Найдём точки пересечения графика с осью абсцисс:
Определим знаки функции на полученных интервалах:
Ответ:
, если ;
, если .
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Что такое производная?
Определение и смысл производной функции
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных.
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции, и, в особенности, бесконечно малые величины. Дело в том, что определение производной базируется на понятии предела, которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций. Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные, в том числе производные сложных функций. Определение определением, смысл смыслом, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования, даже не осознавая сущности своих действий.
Для того, чтобы успешно преподавать математику в условиях жесткой экономии времени репетитору необходимо научиться выделять из потока материала наиболее востребованные на экзамене темы и задачи. Одним из важнейших разделов является метод интервалов (метод промежутков). Если репетитор по математике вовремя раскроет ученику суть алгоритма, это позволит не только открыть перспективу решения большого класса задач на неравенства (логарифмических, показательных, рациональных и иррациональных), но и обеспечить усвоение смежных тем, так или иначе связанных с неравенствами, например, исследование функций.
Какую терминологию использует репетитор по математике?
Как репетитор по математике поясняет правило чередования знаков?
Существует два способа для расстановки знаков между найденными критическими точками:
1) Использование пробных точек в каждом промежутке.
2) Поиск знака в каком-нибудь одном из них с последующим применением законов чередования знаков на всей оси (надеюсь, что репетиторам математики оно известно). Второе удобнее и практичнее, но без первого понять метод знаков чрезвычайно трудно. Некоторые репетиторы по математике ограничиваются тем, что просто сообщают ученику правило перехода через четную и нечетную степень и просто закрепляют его на большом количестве заданий.
Подмеченная закономерность тут же фиксируется репетитором по математике в виде записи правила чередования: при переходе через критическую точку, образованную от линейной скобки в нечетной степени знак на промежутке меняется, а если степень четная – сохраняется. Пожалуй, это основной момент в теме, к пониманию которой репетитор по математике так стремится.
Определение знака в правом промежутке
Советы репетитора по оформлению решений
Отработка моторики действий по выполнению любого математического алгоритма – чрезвычайно важный этап в работе с учеником (особенно с не самым сильным). В методе интервалов есть несколько формальных моментов, о которых репетитор по математике предупреждает ученика и которые желательно соблюдать:
1) При переносе критических точек на рисунок сначала надо пересчитать их количество, затем равномерно распределить по числовой оси, а уже потом прикреплять к ним числа в порядке возрастания. Как часто бывает? Ученик отмечает первую же попавшую ему на глаза критическую точку посередине оси, затем еще одну. После этого выясняется, что третья точка находится между двумя предыдущими, а четвертая между третьей и второй и так далее. В результате информация концентрируются в середине рисунка, и он теряет разборчивость. Приходится переделывать заново.
Инструкция репетитора по математике с поэтапным переносом точек позволяет снижать вероятность не только появления скопления знаков в узкой части рисунка, но и избегать ошибок при расстановке и сравнении. Почему? Потому, что является возможность организовать последовательный перенос точек, от наименьшей до наибольшей. Каждая следующая сравнивается только с предыдущей (в соответствии с порядком возрастания или убывания). Для того, чтобы не пропустить какую-либо из них и быстрее сравнить оставшиеся границы будущих промежутков репетитор по математике вычеркивает отмеченные точки из списка таким образом:
В таком же ключе репетитор по математике настоятельно рекомендует ученику отмечать точки.
2) Знаки на промежутках должны располагаться по другую сторону от прямой (в верхней ее части), а критические точки подписываться по другую сторону (в нижней).
3) Тем самым репетитор по математике расчищает рисунок и делает его более читабельным. Для того, чтобы интервальные знаки не тонули в общей картине их желательно рисовать жирными и длинными.
О выделении промежутков
В учебниках математики, а также на уроках с репетиторами при оформлении решений методом интервалов часто можно встретить загадочные бугорки — кружева, расположенные над промежутками вдоль всей оси. Как и любой другой знак, поставленный репетитором, он должен быть объяснен ученику. Линии не несут никакой смысловой нагрузки, а только выделяют промежутки для того, чтобы они не утонули в потоке пробных точек (изображенных вместе с критическими). Если репетитор по математике отказывается от их использования, то и выделять ничего не нужно. Это является дополнительным аргумент в пользу применения правила чередования знаков. Линиями лучще всего выделять сам ответ.
О выделении критических точек
Нули числителя, как известно, отмечаются согласно знаку неравенства (закрашиваются в случае нестрого знака и выкалываются в случае строгого), а нули знаменателя всегда отмечаются пустыми. Для того, чтобы в голове ученика это обстоятельство надежно отложилось, репетитору по математике следует принять определенные правила оформления записей. Под начальным неравенством проводитяс вертикальная линия. Слева от нее репетитор по математике записывает нули числителя, а справа нули знаменателя. Рядом с каждой колонкой можно указать характер переноса точек на рисунок. Я обычно рисую закрашенную точку у входящих в ответ нулей числителя и пустую точку рядом со списком нулей знаменателя.
О типичных ошибках учеников

Условия применимости метода интервалов должны отработаны репетитором по математике особым образом. Наиболее распространенной ошибкой учащихся в данной теме является использование алгоритма при отсутствии нуля в правой части. Нужно предложить отдельные задания на выявление подобных случаев. Кроме правого нуля выражение в левой части должно быть представлено в виде произведения линейных скобок. У дробей числитель и знаменатель должны быть также разложены на множители. За усвоением этих моментов репетитор по математике обязан следить самым пристальным образом. Кроме ошибок, связанных с условиями применимости метода интервалов, к типичным промахам относится пропуск нулевой критической точки. Она образуется от множителей вида .
Как далеко репетитор по математике углубляется в метод интервалов?
Cуществуют множество ситуаций, которые сводятся к рассматриваемому методу. Одних только алгебраических случаев насчитывается почти с десяток. Это целые и дробные левые частьи, различные комбинации степеней и разложений, совпадения критических точек и сокращения дробей, невозможность разложения скобок на линейные, множители — модули. Если репетитор нацелен дать сильному ученику полноценную подготовку к ЕГЭ по математике, он должен рассмотреть все виды задач. Для логарифмических и показательных неравенств очень актуален расширенный метод интервалов, о котором мы поговорим отдельно.
Оригинальные задания репетитора.
Однотипность любых математических упражнений угнетает даже взрослого ученика. Поэтому для их разнообразия репетитору приходится постоянно что-то выдумывать. В задачах на метод интервалов я использую следующий прием. В качестве дополнения к домашнему заданию предлагаю составить неравенство, левая часть которого имела бы заранее составленное распределение знаков, например:
Нестандартное задание репетитора по математике понравится ученику, а в отдельных случаях поможет стимулировать интерес к занятиям, и, как следствие, к самому предмету.
С уважением, А.Н. Колпаков. Репетитор по математике. Москва. Подготовка к ЕГЭ.
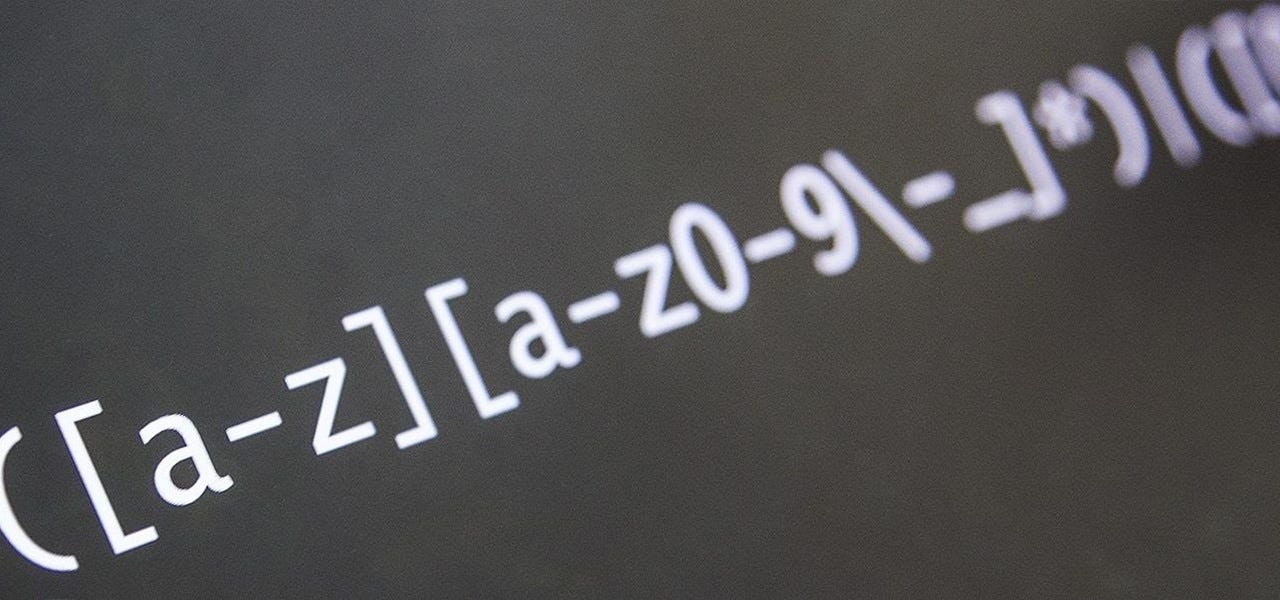
Регулярные выражения (regex или regexp) очень эффективны для извлечения информации из текста. Для этого нужно произвести поиск одного или нескольких совпадений по определённому шаблону (т. е. определённой последовательности символов ASCII или unicode).
Области применения regex разнообразны, от валидации до парсинга/замены строк, передачи данных в другие форматы и Web Scraping’а.
Давайте начнём с нескольких примеров.
Якоря — ^ и $
Квантификаторы — * + ? и <>
Оператор ИЛИ — | или []
Символьные классы — \d \w \s и .
Используйте оператор . с осторожностью, так как зачастую класс или отрицаемый класс символов (который мы рассмотрим далее) быстрее и точнее.
У операторов \d , \w и \s также есть отрицания ― \D, \W и \S соответственно.
Например, оператор \D будет искать соответствия противоположенные \d .
Непечатаемые символы также можно искать, например табуляцию \t , новую строку \n , возврат каретки \r .
Флаги
Мы научились строить регулярные выражения, но забыли о фундаментальной концепции ― флагах.
Регулярное выражение, как правило, записывается в такой форме / abc /, где шаблон для сопоставления выделен двумя слешами / . В конце выражения, мы определяем значение флага (эти значения можно комбинировать):
- g (global) ― не возвращает результат после первого совпадения, а продолжает поиск с конца предыдущего совпадения.
- m (multi line) ― с таким флагом, операторы ^ и $ вызовут совпадение в начале и конце строки ввода (line), вместо строки целиком (string).
- i (insensitive) ― делает выражение регистронезависимым (например, /aBc/i соответствует AbC).
Скобочные группы ― ()
Этот оператор очень полезен, когда нужно извлечь информацию из строк или данных, используя ваш любимый язык программирования. Любые множественные совпадения, по нескольким группам, будут представлены в виде классического массива: доступ к их значениям можно получить с помощью индекса из результатов сопоставления.
Если присвоить группам имена (используя (? . ) ), то можно получить их значения, используя результат сопоставления, как словарь, где ключами будут имена каждой группы.
Скобочные выражения ― []
Помните, что внутри скобочных выражений все специальные символы (включая обратную косую черту \ ) теряют своё служебное значение, поэтому нам ненужно их экранировать.
Жадные и ленивые сопоставления
Например, выражение соответствует
Обратите внимание, что хорошей практикой считается не использовать оператор . , в пользу более строгого выражения:
Границы слов ― \b и \B
\b ― соответствует границе слова, наподобие якоря (он похож на $ и ^ ), где предыдущий символ ― словесный (например, \w ), а следующий ― нет, либо наоборот, (например, это может быть начало строки или пробел).
\B ― соответствует несловообразующей границе. Соответствие не должно обнаруживаться на границе \b .

Если вы спросите, какой способ решения неравенств самый универсальный, мы ответим — метод интервала. Особенно эффективно его использовать для квадратных неравенств с одной переменной. В этой статье расскажем подробный алгоритм и разберем парочку готовых примеров.
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
где x — переменная,
Квадратное неравенство можно решить двумя способами:
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
- D 2 + bx + c.

Если требуется найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
Если неравенство со знаком 2 + 4x - 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).
Определим знак трехчлена x 2 + 4x - 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.
Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.
Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a 0, последовательность знаков: +, +,
если a 2 - 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
- Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
Пример 1. Решить неравенство методом интервалов: x^2 - 5x + 6 ≥ 0.
Неравенство примет вид:
Первый: х - 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х - 3 > 0.
Вывод: знак произведения (х - 3) * (х - 2) меняется только при переходе переменной через значения х = 3 и х = 2.
В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
Вывод: при х > 3 верно неравенство (х - 3) * (х - 2) > 0. Внесем эти данные в чертеж.
Если (х - 3) * (х - 2) > 0:
Если (х - 3) (х - 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.
Читайте также:

