Как сделать уравнение прямой

Добавил пользователь Алексей Ф.
Обновлено: 04.10.2024

В данной статье мы рассмотрим общее уравнение прямой на плоскости. Приведем примеры построения общего уравнения прямой, если известны две точки этой прямой или если известна одна точка и нормальный вектор этой прямой. Представим методы преобразования уравнения в общем виде в канонический и параметрический виды.

Пусть задана произвольная декартова прямоугольная система координат Oxy. Рассмотрим уравнение первой степени или линейное уравнение:

где A, B, C − некоторые постоянные, причем хотя бы один из элементов A и B отлично от нуля.

Мы покажем, что линейное уравнение на плоскости определяет прямую. Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат на плоскости каждая прямая линия может быть задана линейным уравнением. Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат на плоскости определяет прямую линию.

Доказательство. Достаточно доказать, что прямая L определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть на плоскости задана прямая L. Выберем систему координат так, чтобы ось Ox совпадал с прямой L, а ось Oy был перпендикулярной к ней. Тогда уравнение прямой L примет следующий вид:

Все точки на прямой L будут удовлетворять линейному уравнению (2), а все точки вне этой прямой, не будут удовлетворять уравнению (2). Первая часть теоремы доказана.

Пусть задана декартова прямоугольная система координат и пусть задана линейное уравнение (1), где хотя бы один из элементов A и B отличен от нуля. Найдем геометрическое место точек, координаты которых удовлетворяют уравнению (1). Так как хотя бы один из коэффициентов A и B отличен от нуля, то уравнение (1) имеет хотя бы одно решение M(x₀,y₀). (Например, при A≠0, точка M₀(−C/A, 0) принадлежит данному геометрическому месту точек). Подставляя эти координаты в (1) получим тождество

Вычтем из (1) тождество (3):

Очевидно, что уравнение (4) эквивалентно уравнению (1). Поэтому достаточно доказать, что (4) определяет некоторую прямую .

Поскольку мы рассматриваем декартову прямоугольную систему координат, то из равенства (4) следует, что вектор с компонентами x−x₀, y−y₀> ортогонален вектору n с координатами A,B>.

Рассмотрим некоторую прямую L, проходящую через точку M₀(x₀, y₀) и перпендикулярной вектору n (Рис.1). Пусть точка M(x,y) принадлежит прямой L. Тогда вектор с координатами x−x₀, y−y₀ перпендикулярен n и уравнение (4) удовлетворено (скалярное произведение векторов n и равно нулю). Обратно, если точка M(x,y) не лежит на прямой L, то вектор с координатами x−x₀, y−y₀ не ортогонален вектору n и уравнение (4) не удовлетворено. Теорема доказана.

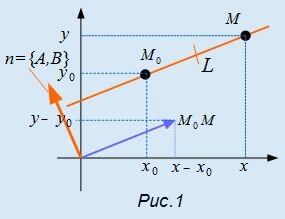Вектор n=A,B> называется нормальным вектором прямой L.

Замечание 1. Если два общих уравнения прямой

определяют одну и ту же прямую, то найдется такое число λ, что выпонены равенства

A₂=A₁λ, B₂=B₁λ, C₂=C₁λ.

(7)

Доказательство. Так как прямые (5) и (6) определяют одну и ту же прямую, то нормальные векторы n₁=A₁,B₁> и n₂=A₂,B₂> коллинеарны. Так как векторы n₁≠0, n₂≠0, то существует такое число λ, что n₂=n₁λ. Отсюда имеем: A₂=A₁λ, B₂=B₁λ. Докажем, что C₂=C₁λ. Очевидно, что совпадающие прямые имеют общую точку M₀(x₀, y₀). Умножая уравнение (5) на λ и вычитая из него уравнение (6) получим:

(A₁λ−A₂)x₀+(B₁λ−B₂)x₀+(C₁λ−C₂)=0.

(8)

Так как выполнены первые два равенства из выражений (7), то C₁λ−C₂=0. Т.е. C₂=C₁λ. Замечание доказано.

Заметим, что уравнение (4) определяет уравнение прямой, проходящей через точку M₀(x₀, y₀) и имеющий нормальный вектор n=A,B>. Поэтому, если известен нормальный вектор прямой и точка, принадлежащая этой прямой, то можно построить общее уравнение прямой с помощью уравнения (4).

Пример 1. Прямая проходит через точку M=(4,−1) и имеет нормальный вектор n=. Построить общее уравнение прямой.

Решение. Имеем: x₀=4, y₀=−1, A=3, B=5. Для построения общего уравнения прямой, подставим эти значения в уравнение (4):

Упростив получим общее уравнение прямой:

Пример 2. Прямая проходит через точки M₁=(−5, 2) и M₂=(−2, 3). Построить общее уравнение прямой.

Решение. Вычислим вектор :

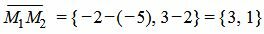Вектор параллелен прямой L и, следовательно, перпердикулярен нормальному вектору прямой L. Построим нормальный вектор прямой L, учитывая, что скалярное произведение векторов n и равно нулю. Можем записать, например, n=.

Для построения общего уравнения прямой воспользуемся формулой (4). Подставим в (4) координаты точки M₁ (можем взять также координаты точки M₂) и нормального вектора n:

Упростим полученное уравнение:

Подставляя координаты точек M₁ и M₂ в (9) можем убедится, что прямая заданная уравнением (9) проходит через эти точки.

Приведение общего уравнения прямой на плоскости к каноническому виду

Нам нужно привести уравнение (1) к каноническому виду. Для этого найдем некоторую точку M₀(x₀,y₀) на этой прямой. Тогда имеем:

Вторую слагаемую уравнения (11) переместим на право и разделим обе части уравнения на −AB:

Мы получили каноническое уравнение прямой. Вектор q=B, A> является направляющим вектором прямой (12).

Обратное преобразование смотрите здесь.

Пример 3. Прямая на плоскости представлена следующим общим уравнением:

Привести данное уравнение прямой к каноническому виду.

Решение: Найдем некоторую точку на прямой (13). Для этого подставим в (13) y=1 и найдем x. Получим x=2. Запишем уравнение прямой пользуясь формулой (11):

Переместим на право вторую слагаемую и разделим обе части уравнения на 2·5:

Приведение общего уравнения прямой на плоскости к параметрическому виду

В предыдущем параграфе мы привели общее уравнение прямой (1) к каноническому виду (12). Из канонического уравнения легко получить параметрическое уравнение прямой. для этого левый и правый части уравнения (12) обозначим через параметр t. Тогда получим:

Выразив x и y через параметр t, получим параметрическое уравнение прямой:

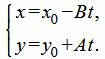Обратное преобразование смотрите здесь.

Пример 4. Прямая на плоскости представлена следующим общим уравнением:

Привести данное уравнение прямой к параметрическому виду.

Решение: Найдем некоторую точку на прямой (13). Для этого подставим в (14) x=3 и найдем y. Получим y=11. Запишем уравнение прямой пользуясь формулой (11):

Переместим на право вторую слагаемую и разделим обе части уравнения на 5·2:

Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.

Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.

Уравнения прямой, проходящей через две точки могут быть следующих видов:

каноническое уравнение,
параметрическое уравнение,
общее уравнение прямой,
уравнение прямой с угловым коэффициентом,
уравнение прямой в полярных координатах и другие.

Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.

В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.

Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.

В тригонометрии есть задачи, в которых нужно найти уравнение прямой. При этом даны либо координаты одной точки и угловой коэффициент, либо координаты двух точек, которые лежат на прямой. В любом случае найти уравнение прямой довольно легко, если использовать соответствующие формулы.

Например, угловой коэффициент k = 2, тогда уравнение запишется так: y-y₁= 2 (x-x₁).

Например, если дана точка с координатами (4,3), уравнение запишется так: y-3 = 2(x-4).

Например, даны две точки с координатами (3, 8) и (7, 12). Тогда формула запишется так: k = (12-8)/(7-3) = 4/4 = 1. В этом примере угловой коэффициент k = 1.

В нашем примере уравнение прямой запишется так: y = 1x + b или y = x + b.

В нашем примере возьмем точку с координатами (3, 8). Тогда уравнение прямой запишется так: 8 = 1(3) + b.
Используйте координаты одной из двух данных точек, но никогда не смешивайте координаты сразу двух точек.

В нашем примере уравнение прямой, которая проходит через точки с координатами (3, 8) и (7, 12), запишется так: y = 1x + 5 или просто y = x + 5.

Дополнительные статьи

Об этой статье

В данном материале рассмотрим, что такое уравнение прямой. Проанализируем каждый вид данного уравнения. Изучим основные формулы и графики. Применим весь рассмотренный материал на практике, в виде решения задач и уравнений.

Данное уравнение - характеризуется, как уравнение двух переменных значений.

Значения в математики, чаще всего обозначают буквами x и y. Это самое распространенное обозначение, однако можно встретить и другие буквенные обозначения. Например: z, n и другие значения.

Определение прямой линии- фигура, состоящая из множества простых точек. Каждая точка, имеет собственные, определенные координаты, относительно осей абсцисс и ординат.

Уравнение прямой на плоскости - уравнение, характеризующее взаимосвязь координатных значений точек на прямой.

Для решения уравнений необходимо помнить ряд важным математических функций, правил, значений.

Все их мы будем рассматривать подробно в каждом разделе на примерах решения.

Общее уравнение прямой линии системы координат

Рассмотрим соответствующую теорему, которая отражает уравнение прямой на плоскости в системе координат Oxy.

Подробно исследуем следующее уравнение: ax+by+c=0.

Значения х и y, являются переменными данными со значениями.

a и b - действительные простые числа. Обязательное условие, которых неравенство нулю.

Следовательно, прямая линия задается вышеупомянутым уравнением данного вида: ax+by+c=0.

Рассмотрим на примере изученную теорему:

На данном рисунке, мы рассмотрим красную линию и запишем уравнение для нее.

Координаты на данной прямой удовлетворяют составленному уравнению.

Уравнение может быть также полным и неполным. Рассмотрим случаи:

Все действительные числа, имеют любое значение, но не равные нулю. Поэтому такое определение относится к данному типу уравнений.

Все числа в уравнении имеют любое значение. Характерно, также значения отрицательных знаков.

Уравнение прямой в отрезках прямой

Для отрезков уравнение будет иметь следующей вид:

Данные в знаменателе, являются действительными значениями, не равными нулевому значению. Величины действительных данных равняются отрезку. Он отсоединяется линией на оси координат. Протяженность начинает свой отсчет от начала координатной прямой.

Пример:

Нужно начертить прямую линию, которая задается формулой.

Обозначим на графике две точки ( 3 ; 0 ) , (0; \[-\frac\]). Далее необходимо их соединить между собой.

Уравнение прямой с угловым коэффициентом

Записываем уравнение вида: \[\mathrm=\mathrm \cdot x+b\];

x - значение, которое принимается, как переменное;

к - простое действительное число, является показателем углового коэффициента;

b - действительное число.

Угол наклона на плоскости в системе координат - угол, который берет свой отсчет значений от направления с положительным знаком до прямой, которая направлена против хода часовой стрелки.

Угол будут считать нулевым, если прямая линии, имеют параллельное расположение относительно оси абсцисс либо совпадает с ней по расположению. Угол принимает значения, согласно интервалу (0, \[\pi\]).

Угловой коэффициент - значение тангенса угла наклона этой же прямой линии.

В случае, когда прямая линия параллельная другой оси, ординат, то принято считать, что угловой коэффициент не определяется. И соответствует интервалу бесконечности.

График функции будет возрастать, если значение коэффициента имеет положительное значение. Следовательно, убывание будет наблюдаться в противоположном значение, а именно с отрицательным значением.

На графиках показаны значения угловых коэффициентов и угол наклона. Когда есть разное расположение относительно осей.

На примерах рассмотрим нахождение углового коэффициента. Для этого из прошлых тем, вспомним определение тангенса и его вычисление.

Пример №1:

Угол наклона прямой равен 120 градусов, относительно оси ох.

Нам нужно определить угловой коэффициент.

Применим известные нам формулы и подставим данные.

Следовательно правильный ответ задачи будет равняться \[k=-\sqrt\]

Пример №2:

В этом примере нам уже известно значение углового коэффициента.

Нужно определить угол наклона, относительно прямой. Для этого, нужно обязательно учитывать знак известного коэффициента. Если к>0, следует что угол будет острый и определяться как \[\alpha=\operatorname k\].

Когда к

Важные моменты, которые следует помнить, при решении задач с каноническим уравнением.

Отметим следующие важные факты:

если вектор является прямым и прямая линия проходит через точку, то ее уравнение имеет вид : \[\frac>>=\frac>>\]
когда вектор прямой по направлению, то любой из векторов может быть направляющим вектором прямой. И уравнение записывается следующим образом: \[\frac><\mu \cdot \alpha_>=\frac><\mu \cdot \alpha_>\]

Пример №1:

Прямая в системе координат проходит через точки (2;-4) и вектор направляющий равен (1;-3). Составьте и напишите каноническое уравнение, применяя известные нам данные.

Следовательно уравнение записывается следующим образом: \[\frac>>=\frac>> \Leftrightarrow \frac=\frac \Leftrightarrow \frac=\frac\]

Пример №2:

Составить каноническое уравнение, проходящее через точки \[\sqrt[3] ; \quad-\frac\]

Прямая является параллельной относительно оси координат. Направляющий вектор принимается \[\underline=(0 ; 1)\]. Учитывая значение точек, через которые проходит прямая, записываем уравнение:

Пример №3:

Составим уравнение, руководствуясь графиком, приведенным ниже.

Из рисунка видно, что прямая проходит через точки со значениями (0;3). Расположена параллельно относительно оси x (ось абсцисс). Координатный вектор \[\underline=(1,0)\] - направляющий вектор, для данной системы.

Читайте также: