Как сделать спектральный график в маткаде
Добавил пользователь Владимир З. Обновлено: 04.10.2024
Mathcad является универсальным инструментом у тех людей, которые плотно связали свою жизнь с вычислениями. "Маткад" способен производить сложные математические расчеты и мгновенно выдавать ответ на экране. Студенты или те, кто в первый раз столкнулся с этой программой, задают множество вопросов, на которые не могут дать ответ самостоятельно. Один из них, затрудняющий дальнейшее обучение: как построить график в "Маткаде"? На самом деле, это не так сложно, как может показаться. Постараемся разобраться также в том, как в "Маткаде" построить график функции, как строить несколько функций, узнаем о некоторых элементах отображение графика на экране.
Быстрый график в Mathcad
Вам будет интересно: Пуристы - это. Значение слова
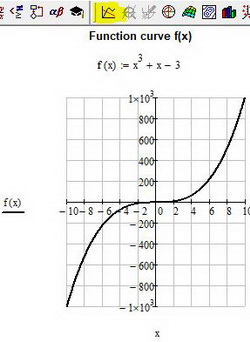
Возьмем одну функцию и будем проводить все ниже перечисленные операции с ней. Допустим, имеем следующее техническое задание: построить график функции f(x) = (e^x/(2x-1)^2)-10 на интервале [-10;10], исследовать поведение функции.
Итак, перед тем как построить график в "Маткаде", нужно переписать нашу функцию в математическую среду. После этого просто прикинем возможный график без масштабирования и всего прочего.
Построение дополнительных графиков
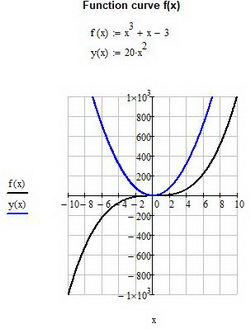
Чтобы понять, как построить несколько графиков в "Маткаде", добавим к нашему техническому заданию небольшое дополнение: построить график производной от заданной функции. Единственное, что нам нужно - в поле графика добавить производную по переменной "x".
График, построенный по набору значений
Перед тем как построить график в "Маткаде" по точкам, необходимо создать диапазон значений. Сразу отметим, что график, построенный по точкам, иногда бывает неточным, так как может найтись такая точка, которая не попадет в диапазон значений, но в оригинальном графике в ней происходит разрыв. В этом примере специально будет показан этот случай.
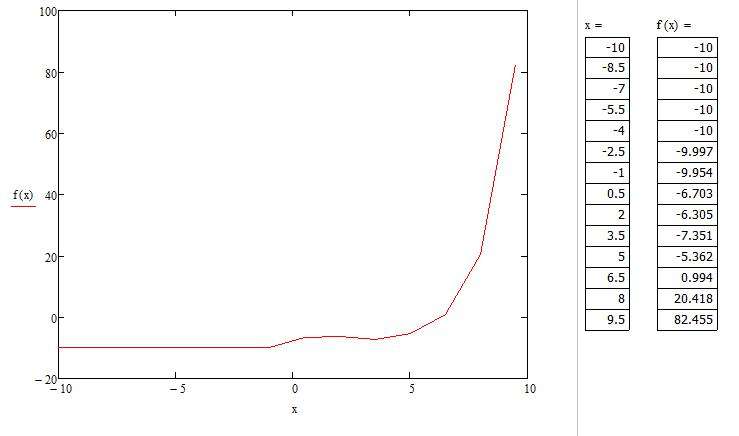
Мы видим, что на графике, построенном по точкам, не отображается та точка, которая осуществляет разрыв на исходном графике. То есть можно сделать вывод о том, что построение по точкам может не учитывать значения функции, которые создают разрыв.
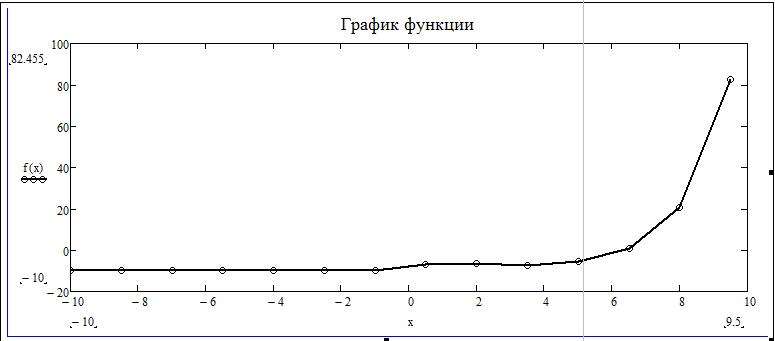
Настройка отображения графика
В этой статье мы уже затрагивали настройки графика. Окно с настройками вызывается двойным нажатием левой кнопкой мыши по графику. В окне форматирования графика есть пять разделов. "Оси X, Y" - содержит информацию про координатные оси, а также отображения вспомогательных элементов. Второй раздел "Трассировка" связан с кривыми линиями построения графика, здесь можно корректировать их толщину, цвет и другое. "Формат числа" отвечает за отображение и расчет единиц. В четвертом разделе можно добавлять подписи. Пятый раздел " По умолчанию" выводит все настройки в стандартную форму.
| Название работы | Кол-во страниц | Размер |
| Конспект лекций Таганрог 2001 (075. 8) Механцев Е. Б | 4 | 666.88kb. |
| Об обеспечении образовательного процесса оборудованными учебными. | 1 | 37.06kb. |
| Об обеспечении образовательного процесса оборудованными учебными. | 1 | 50.57kb. |
| Об обеспечении образовательного процесса оборудованными учебными. | 1 | 226.82kb. |
| Справка №4 об обеспечении образовательного процесса оборудованными. | 1 | 83.79kb. |
| Председатель пк | 1 | 71.81kb. |
| Методические указания по проведению практических занятий на тему. | 1 | 230.79kb. |
| Тематический план лабораторно-практических занятий № п/п | 1 | 31.6kb. |
| Академическая мобильность студентов | 1 | 14.28kb. |
| Тематический план практических занятий | 1 | 10.42kb. |
| Методические рекомендации для практических занятий разработаны на. | 1 | 212.22kb. |
| Оснвные понятия об электрических цепях переменного тока | 1 | 44.41kb. |
| Направления изучения представлений о справедливости | 1 | 202.17kb. |
1.2.Спектральные характеристики непериодических сигналов
1.2.1.Основные понятия и соотношения
Спектральное представление можно обобщить на случай, когда функция x(t) — непериодическая, т.е. T. В этом случае применяется интегральное преобразование Фурье
(обратное), где (1.6)
Здесь Ф и Ф -1 - обозначения прямого и обратного оператора Фурье .
Формулы (1.6) и (1.7) — пара интегральных преобразований Фурье. Функция F(j) называется спектральной функцией или комплексным спектром непериодического сигнала. Она определена при положительных и отрицательных частотах.
Спектральную функцию можно представить в виде
где - спектр амплитуд; - спектр фаз.
1.2.2.Типовые примеры
Пример 1.2.1. Найти спектр функции , заданной на интервале -2t/2, при исходных данных: ; ; возможная периодичность повторения (рис.1.2.1).
Аналитическое выражение функции
Решение. Поскольку функция представляет собой непериодическую функцию времени, найдем ее спектральную функцию (комплексный спектр) на основании интегрального преобразования Фурье (1.7). Оперируя безразмерными величинами, следует помнить, что спектральная функция характеризует спектральную плотность амплитуд и фаз элементарных комплексных гармонических колебаний . Она имеет для сигнала в виде напряжения размерность вольт секунда. Угловая частота имеет размерность радиан/секунда.
Так как заданная функция является четной, то ее спектр должен быть вещественной функцией. Для представления вещественной функции достаточен один график.
Интегральное преобразование Фурье
Интегрирование дает действительную функцию
Полученное выражение запишем в компактной форме, введя определение функции отсчетов
Тогда, умножая числитель и знаменатель спектральной функции на2, ее можно записать в виде
Эта спектральная функция при=0 имеет неопределенность вида 0/0. Раскроем неопределенность по правилу Лопиталя
График спектральной функции приведен на рис.1.2.2 при , изменении угловой частоты с шагом в долях частоты первой гармоники и числе гармоник (в случае периодического продолжения), а именно при .
Амплитудный спектр определяется как модуль спектральной функции, т.е.
Переход от действительной и знакопеременной спектральной функции к амплитудному спектру требует введения фазового спектра. При взятии модуля спектральная функция изменяет фазу на 180 0 = (при и ) в точках , когда значения .
Таким образом, фазовый спектр
рафики амплитудного и фазового спектров приведены на рис.1.2.3 и 1.2.4.
Отсюда следует спектральная функция в экспоненциальной форме (рис.1.2.5)
Пример 1.2.2. Найти спектр синусоидальной функции z(t) , заданной на интервале -2t 2, при исходных данных: амплитуда ; длительность ; при частота или ; возможная периодичность повторения (рис.1.2.6 при ).
Аналитическое выражение функции
Решение. Интегральное преобразование Фурье
Представим подынтегральное выражение в экспоненциальной форме. Согласно формуле Эйлера, имеем
Тогда интеграл приводится к виду
С учетом введения функции отсчетов
после интегрирования получим
Так как функция z(t) является нечетной, то ее спектр представляется чисто мнимой функцией Fz()=jMz(), где мнимая часть
График мнимой части спектральной функции приведен на рис.1.2.7 при и .
Учитывая соотношение , спектральную функцию можно записать в экспоненциальной форме
Экспоненциальный множитель здесь определяет фазовый спектр
Амплитудный спектр это модуль спектральной функции, т.е.
Переход от знакопеременной мнимой части спектральной функции к амплитудному спектру требует введения дополнительного фазового спектра. При взятии модуля функция изменяет фазу на 180 0 = в точках, когда . Поэтому дополнительный фазовый спектр
Полный фазовый спектр синусоидальной функции z(t) принимает вид
Графики амплитудного и фазового спектров приведены на рис.1.2.8 и 1.2.9 при и .
В конечном итоге спектральную функцию можно выразить через амплитудный и фазовый спектры, представив ее в экспоненциальной форме
Эту задачу можно также решить, используя теорему о переносе спектра. В нашем случае функция z(t) есть результат умножения функции x(t) из примера 1.2.2 на синусоиду . Последняя, согласно соотношению Эйлера, представляется с точностью до множителя 1/2j разностью двух экспонент и . Поэтому на основании теоремы спектр функции z(t) будет представлять собой разность двух спектров, а именно спектра функции x(t), перенесенного на частоту +0, и спектра функции x(t), перенесенного на частоту -0. Одновременно при переносе значения исходного спектра уменьшаются в два раза за счет множителя 1/2j. На основании изложенного, зная спектр функции x(t)
спектр функции z(t) можно записать следующим образом:
График мнимой части спектральной функции Fz(), соответствующей этой форме записи, приведен на рис.1.2.10. Он аналогичен графику на рис. 1.2.7.
Пример 1.2.3. Построить спектры амплитуд и фаз одиночного прямоугольного видеоимпульса при исходных данных: амплитуда ; длительность ; начальный момент времени ; возможная периодичность повторения (рис.1.2.11 при ).
Математическая модель сигнала
Решение. Поскольку сигнал представляет собой непериодическую функцию времени, найдем спектральную функцию (комплексный спектр) импульса P(t) на основании интегрального преобразования Фурье (1.7). Так как сигнал - нечетная функция, то его спектр должен быть комплексной функцией.
Интегральное преобразование Фурье
или при записи в форме a+jb
1) действительная часть ;
Данная спектральная функция при =0 имеет неопределенность вида 0/0. Раскроем неопределенность по правилу Лопиталя
Значение предела будет . Таким образом, при =0 значение спектральной функции .
Амплитудный спектр сигнала определяется как модуль спектральной функции, т.е.
С учетом особой точки =0 амплитудный спектр представляется выражением
Фазовый спектр (как аргумент спектральной функции)
Подстановка действительной и мнимой частей спектральной функции дает
Графики амплитудного и фазового спектров приведены на рис.1.2.12 и 1.2.13 при изменении угловой частоты в долях частоты первой гармоники в случае периодического продолжения импульсного сигнала, а именно при
Для области физически реализуемых частот (f>0) графики амплитудного и фазового спектров приведены на рис.1.2.14 и 1.2.15 при изменении частоты в долях частоты первой гармоники в случае периодического продолжения импульсного сигнала, а именно при и .
Пример 1.2.4. Решить задачу из примера 1.2.3 на основе теоремы о временном сдвиге.
Решение. Согласно данной теореме временной сдвиг сигнала , например, на величину эквивалентен умножению в частотной области его спектральной функции на комплексную экспоненту . При этом амплитудный спектр исходного сигнала не изменяется. Изменится только спектр фаз на величину .
Перенесем начало координат в середину импульса путем его временного сдвига на величину . Это дает нам четную функцию P1(t) сдвинутого сигнала (рис.1.2.16)
Для четной функции импульса P1(t) его спектральная функция Fp1() будет вещественной, а для нечетной - чисто мнимой.
Воспользуемся решением примера 1.2.1. Из этого примера следует, что спектральная функция симметричного относительно начала координат прямоугольного видеоимпульса с точностью до множителя будет иметь вид функции отсчетов
Таким образом, спектральная функция сдвинутого сигнала
Вернемся к исходному сигналу, сдвинув по времени симметричный видеоимпульс на величину . При этом на основании теоремы о временном сдвиге можно получить спектральную функцию исходного видеоимпульса
Амплитудный спектр сигнала определяется как модуль спектральной функции
Фазовый спектр (как арктангенс отношения мнимой и действительной частей спектральной функции)
или после подстановки действительной и мнимой частей
Графики амплитудного и фазового спектров приведены на рис.1.2.17 и 1.2.18 при изменении угловой частоты в долях частоты первой гармоники в случае периодического продолжения импульсного сигнала с периодом T, а именно при
Фазовые спектры на рис.1.2.13 и 1.2.18 аналогичны и соответствуют периодической форме представления линейного фазового спектра. Убедимся в этом. Выражение
с учетом тригонометрического равенства
приводится при = к виду фазовой характеристики примера 1.2.3, т.е.
С другой стороны, так как
то отсюда имеем линейную форму представления фазового спектра (рис.1.2.19)
Пример 1.2.5. Сигнал в частотной области имеет:
а) равномерный спектр амплитуд (параметры - плотность амплитуд и частота среза спектра )
б) линейный спектр фаз (параметр )
Требуется найти вид этого сигнала.
Графики частотных характеристик приведены на рис.1.2.20 и 1.2.21 при и .
Решение. Спектральная функция сигнала U(t) в экспоненциальной форме
Вид сигнала можно найти обратным преобразованием Фурье (1.4) его спектральной функции:
Полученное выражение можно записать в компактной форме, если умножить его числитель и знаменатель на c и учесть определение функции отсчетов
В результате получим
График сигнала приведен на рис.1.2.22 при
1.2.3.Типовые задачи
Задача 1.2.1. Построить спектры амплитуд и фаз сигнала U(t) на выходе генератора линейно изменяющегося напряжения (ГЛИН) при исходных данных: скорость изменения и длительность (рис.1.2.23) .
Аналитическое выражение сигнала
Ответ. Амплитудный спектр
.
Задача 1.2.2. Найти спектр косинусоидальной функции y(t) , заданной на интервале -2t 2 и показанной на рис.1.2.24, при исходных данных: амплитуда ; длительность ; при частота или ; возможная периодичность повторения .
Аналитическое выражение функции
Ответ. Спектр функции y(t)
.
Задача 1.2.3 Найти амплитудный спектр одиночного видеоимпульса синусоидальной формы (рис.1.2.25) при исходных данных: амплитуда ; длительность ; при частота (угловая частота ) и период .
Аналитическое выражение сигнала:
Ответ. Амплитудный спектр
График амплитудного спектра видеоимпульса S(t) синусоидальной формы приведен на рис.1.2.26 при изменении угловой частоты в долях несущей частоты в случае периодического продолжения импульсного сигнала с периодом T0, а именно при
Задача 1.2.4. Решить задачу 1.2.3 с использованием теоремы о временном сдвиге.
Ответ. Амплитудный спектр
.
Задача 1.2.5. Найти спектры амплитуд и фаз экспоненциального видеоимпульса , с амплитудой и коэффициентом затухания (рис.1.2.27).
Математическая модель сигнала
Ответ. Амплитудный спектр
.
Задача 1.2.6. Найти амплитудный спектр экспоненциального радиоимпульса , (рис.1.2.28) с параметрами: амплитуда ; коэффициент затухания ; несущая частота ().
Математическая модель сигнала
Ответ. Амплитудный спектр экспоненциального радиоимпульса
График амплитудного спектра приведен на рис.1.2.29 при , и изменении угловой частоты .
Задача 1.2.7. Найти в рамках Mathcad 6.0 спектры некоторых специальных функций:
1) дельта-функция или функция Дирака
2) единичный скачок или функция Хевисайда [спецфункция Mathcad Ф(t)]
3) комплексная синусоида (пусть )
4) бесконечная косинусоида при (и, например, )
5) постоянная функция .
ПРИМЕЧАНИЕ. Все эти функции абсолютно неинтегрируемы, но путем предельного перехода для них можно найти интегральное преобразование Фурье.
Ответ. Спектральные функции:
1) - вещественна, постоянна и равна 1 на любой частоте;
2) , где Dirac()=() - дельта-функция в частотной области;
ПРИМЕЧАНИЕ. Если интеграл непосредственно не берется, то следует использовать в Mathcad команды прямого преобразования Фурье “Fourier Transform” и обратного преобразования Фурье “Inverse Fourier Transform” меню Symbolic и Transforms.
Задача 1.2.8. Амплитудный спектр сигнала S(t) имеет параметры:
а) плотность амплитуд ;
б) частоты среза спектра и .
Амплитудный спектр описывается выражением
Спектр фаз равен нулю. Требуется найти вид сигнала S(t).
График частотной характеристики (амплитудного спектра) приведен на рис.1.2.30 при и .
Ответ. Сигнал
причем при t=0 имеем
График сигнала при и приведен на рис.1.2.31.
Задача 1.2.9. Найти амплитудный спектр одиночного видеоимпульса специальной формы (рис.1.2.32) с параметрами: значения амплитуд и ; длительность ; начальный
момент времени ; возможная периодичность повторения .
Аналитическое выражение сигнала
ПРИМЕЧАНИЕ. Для решения данной задачи целесообразно использовать принцип суперпозиции и теорему о временном сдвиге.
Ответ. Амплитудный спектр одиночного видеоимпульса специальной формы
График амплитудного спектра приведен на рис.1.2.33 при
Чем хуже память, тем лучше помнишь старое доброе время.
ещё >>

В статье рассмотрены основные возможности построения графиков в программе mathcad. Для инженерных и студенческих расчетов, как правило, достаточно знать следующие методы построения графиков:
Построение графика по точкам
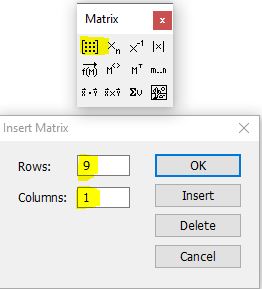
Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)
Рис. 1. Создание матриц-столбцов
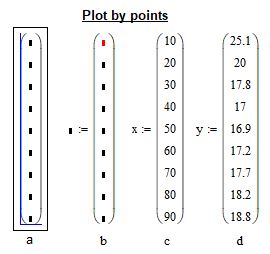
В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш "стрелка" и "пробел" добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия ":". У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.
Рис. 2. Заполнение матриц-столбцов для графика
На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши. У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)
Рис. 3. Создание заготовки для графика
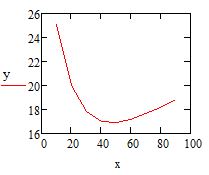
Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)
Рис. 4. График по точкам
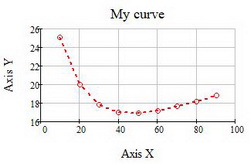
Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)
Рис. 5. Настройка отображения графика
Построение графика функции f(x)
Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием ":=" (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой
Рис. 6. Построение графика функции f(x)
Чтобы построить два графика и более на одном поле (в тех же осях координат) сделайте следующее: введите вторую функцию, например y(x):=. , поместите курсор мыши в маркер поля графика, где уже указана первая функция f(x) и введите запятую. Таким образом mathcad зоздаст второй маркер для ввода очередной функции. Введите вашу вторую функцию и нажмите enter. Если имя аргумента обеих функций совпадает, то вторая кривая отобразится в поле графика, в противном случае, под осью абсцисс введите через запятую имя аргумента второй функции. Образец можно посмотреть ниже на рис. 7
Рис. 7. Построение двух графиков функции
Построение эпюры в mathcad
Чтобы построить классическую эпюру в mathcad нужно выполнить следующие действия:
- ввести функцию в виде y = f(x), как это показано в примерах выше;
- ввести такназываемую ранжинрованную переменную в виде i = a, a-dt..b с определенным шагом dt;
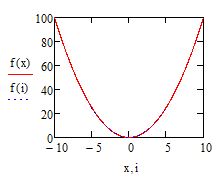
- создать поле графика и ввести туда функции f(x) и f(i) с соответствующими аргументами
- настроить визуализацию функции f(i) в соответствии с требованиями к оформлению эпюр в вашем ВУЗе или компании
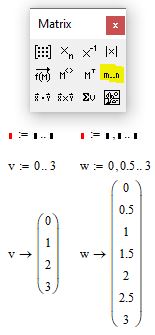
Ранжированная переменная по сути является матрицей-столбцом, разница лишь в том, что значение элементов в нее входящих представляют из себя определенную закономерность или последовательность чисел. Ранжированную переменную можно ввести воспользовавшись кнопкой Range Variable из панели Matrix. Первый маркер отвечает за начальное значение последовательности, второй - за конечное. По умолчаию шаг последовательности равен 1. Если после первого элемента ввести символ запятой и в появившемся маркере ввести следующее число вашей последовательности, то таким образом вы определите шаг, с которым будет заполняться ваша последовательность. Обратите внимание на пример ниже.
Рис. 8. Ввод ранжированной переменной
Ранжированные переменные можно использовать для построения эпюр распределения физических величин. Для этого постройте ваш исходный график одним из методов, описанных выше. Пусть это будет график f(x):=x^2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже
Рис. 9. Ввод ранжированной переменной
Далее создайте поле для графика и около оси ординат введите две функции: f(x) и f(i). Под осью абсцисс также введите соответсвующие аргументы: x и i. Вы должны увидет обычную параболу как на рисунке ниже
Рис. 10. Построение эпюры. Шаг 1
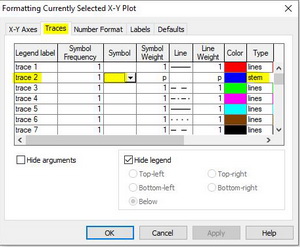
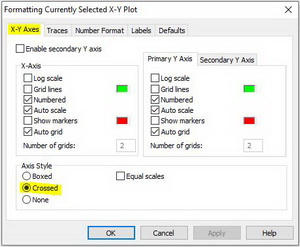
Для получения эпюры нужно настроить отображение функции f(i) в свойствах графика. Щелкните 2 раза по графику чтобы вызвать меню настройки отображения графика. Перейдите во вкладку traces. В списке Legend Label найдите имя trace 2. В столбце Type для trace 2 из выпадающего списка выберете тип графика stem. В столбце Symbol уберите отображение элементов. Во вкладке X-Y Axes выберете для Axis Style тип Crossed. Нажмите ОК и вы увидете эпюру. Вы можете настроить ее внешний вид по желанию.
Рис. 11. Построение эпюры. Шаг 2
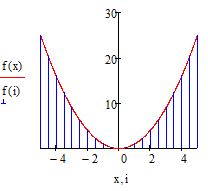
В итоге вы увидите, что на графике появились вертикальные линии, которые распределены по оси абсцисс с шагом, который вы указали в ранжированной переменной. Изменяя параметры этой переменной можно настроить отображение эпюры. Эпюра готова (см. рис. 12)
Рис. 12. Построение эпюры. Шаг 3
Построение графика в полярных координатах в mathcad
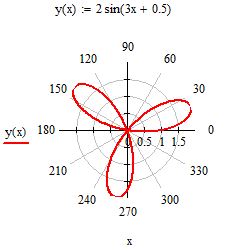
Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)
Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph
Рис. 13. Создание загатовки для графика в полярных координатах
Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter. Вы увидете "трилистник". Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.
Рис. 14. Построение графика в полярной системе координат

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
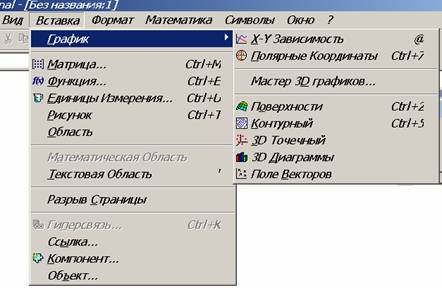
Основные операции при построении графика . При построении графика необходимо выполнить следующие шаги:
· щелкнуть мышью в том месте, где нужно создать график;
· обратиться к пункту Вставка, командам График – Х-У Зависимость. В рабочем документе создается пустой график с шестью полями ввода;
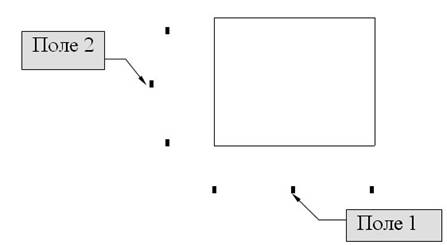
Другие четыре поля используются для выбора границ на осях координат
Пример. В рабочем документе постройте график функции f(x)=x 2 + x для x меняющимся от -10 до 10 с шагом 0.1.
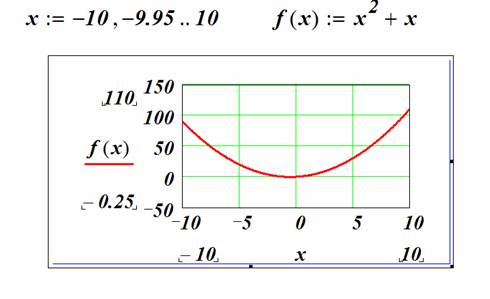
Форматирование и редактирование графиков
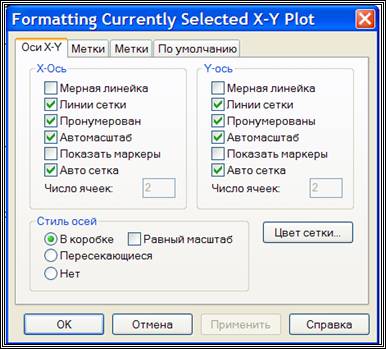
Для изменения формата осей, способа их оцифровки, цвета графиков необходимо:
· щелкнуть мышью на графике, чтобы он заключился в синюю рамку;
· обратиться к появившемуся пункту X-Y-Plot, команде Format;
· используя закладки X-Y-оси, Графики, надписи выполнить форматирование
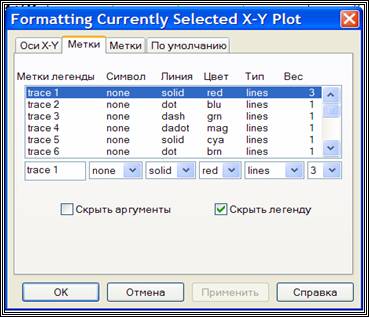
Построение нескольких графиков
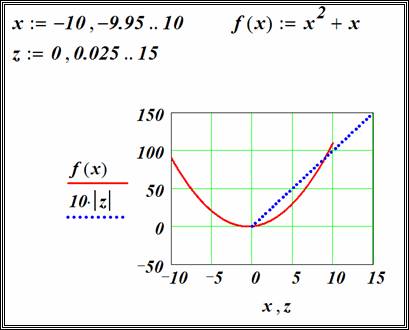
Графическое представление вектора
Графики в полярной системе координат
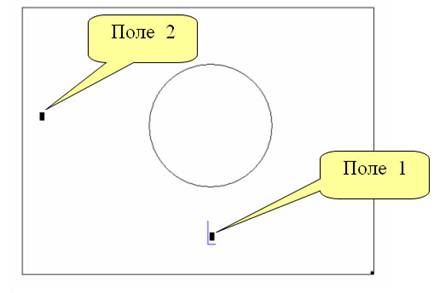
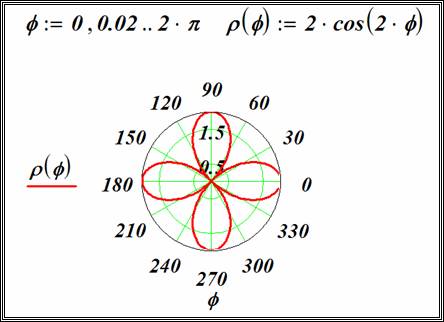
Форматирование графика
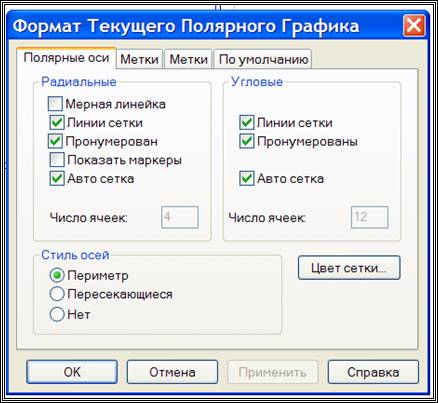

График параметрической функции
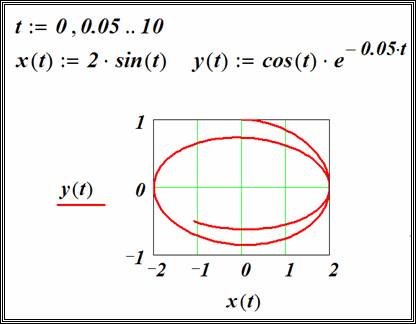
Графики функций двух переменных (поверхностей)

Для создания трехмерного графика (графика функции двух переменных) необходимо щелкнуть на одной из следующих кнопок палитры Графика с изображением требуемого типа графика. В документе появится шаблон графика с тремя осями и пустым полем. В это поле вводится либо имя массива, либо имя функции двух переменных.
В первом случае предварительно необходимо сформировать матрицу из значений функции в узлах прямоугольной сетке.
Во втором случае предварительно надо описать функцию от двух переменных.
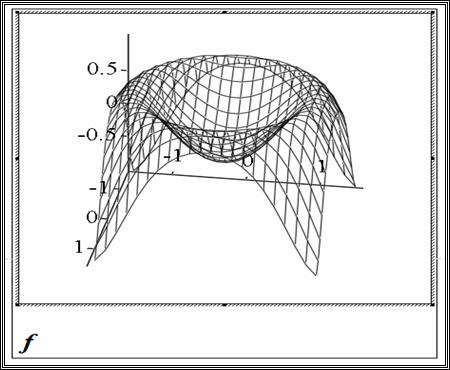
Пример построения графика с формированием матрицы. Необходимо построить график функции
f ( x , y ) = Sin ( x 2 + y 2 ) для x [-1.5, 1.5] , y [-1.5, 1.5]

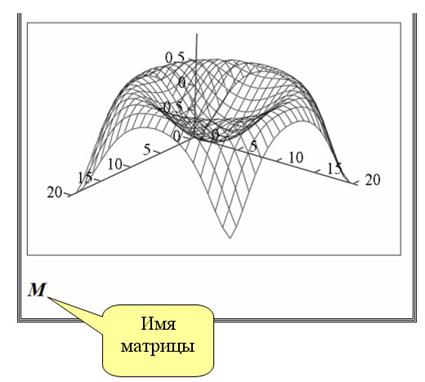
Форматирование графика
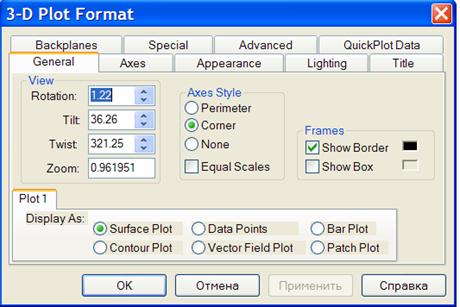
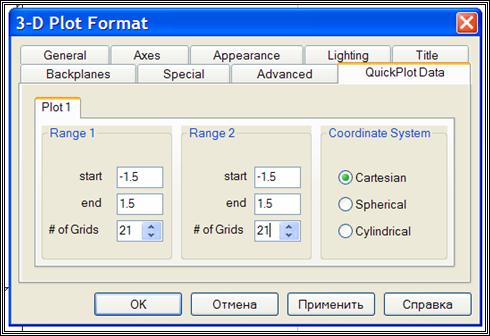
Окно форматирования трехмерных графиков вызывается аналогично и имеет ряд вкладок:
· общие – установка общих параметров форматирования;
· ось – установка параметров форматирования координатных осей;
· вид – установка вида графика;
· освещение – задание условий освещения и выбор схемы освещения;
· название – задание титульных надписей и их параметров;
· основание – установка параметров форматирования граней;
· особый – задание специальных эффектов форматирования;
· дополнительно – установка дополнительных параметров;
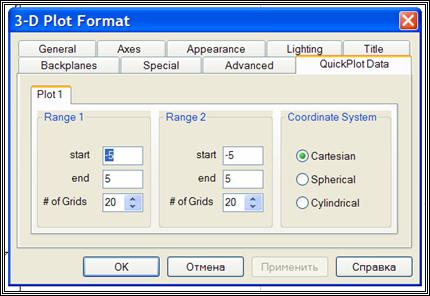
· данные QuickPlot – параметры быстрого построения графика.
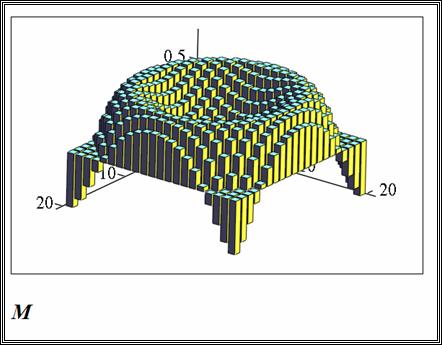
Автоматическое формирование матрицы
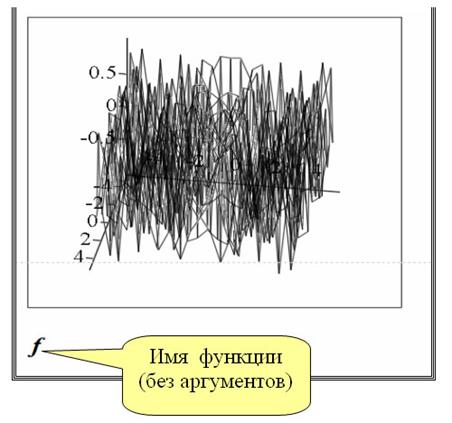
Графики векторных полей
Для отрисовки векторного поля ( в каждой точке такого поля задается не скалярная величина, а вектор с двумя проекциями ) необходимо :
· вычислить две матрицы ( первая содержит проекции вектора на ось Х, вторая на ось У ) или сформировать комплексную матрицу;
· обратиться к пункту меню Graphics , команде Create Vector Field Plot ;
· заполнить в нижней части появившегося шаблона поле, введя туда имена двух вещественных массивов или имя одного комплексного массива.
Читайте также: