Как сделать прямоугольник из пентамино
Добавил пользователь Дмитрий К. Обновлено: 05.10.2024
Если рассматривать вращения фигур на 90°, то существуют следующие категории симметрии:
- L, N, P, F и Y могут быть ориентированы 8 способами каждая: 4 поворотами и ещё 4 зеркальными отображениями.
- Z может быть ориентирована 4 способами: 2 — поворотами, 2 — зеркальными отображениями.
- T, V, U и W могут быть ориентированы поворотами 4 способами каждая.
- I может быть ориентирована поворотами 2 способами.
- X может быть ориентирована единственным способом.
Отсюда число фиксированных пентамино равно 5 × 8 + (1 + 4) × 4 + 2 + 1 = 63.
Например, вот восемь возможных способов ориентации пентамино L, F, P, N и Y:
Укладка прямоугольников
Самая распространённая задача в пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20. Каждую из этих головоломок можно решить вручную, но более сложной задачей является подсчёт общего числа возможных решений в каждом случае (очевидно, прямоугольники 2 × 30 и 1 × 60 составить из пентамино невозможно, поскольку многие фигуры в них просто не помещаются по ширине).
Для случая 6 × 10 эту задачу впервые решил в 1965 году Джон Флетчер [2] . Существует 2339 различных укладок пентамино в прямоугольник 6×10, не считая поворотов и отражений целого прямоугольника, но считая повороты и отражения его частей (иногда внутри прямоугольника образуется симметричная комбинация фигур, поворачивая которую, можно получить дополнительные решения; для прямоугольника 3×20, приведённого на рисунке, второе решение можно получить поворотом блока из 7 фигур, или, иначе говоря, если поменять местами четыре фигуры, крайние слева, и одну крайнюю справа).
Для прямоугольника 5 × 12 существует 1010 решений, 4 × 15 — 368 решений, 3 × 20 — всего 2 решения (отличающихся вышеописанным поворотом). В частности, существует 16 способов сложить два прямоугольника 5 × 6, из которых можно составить как прямоугольник 6 × 10, так и 5 × 12.
Укладка прямоугольников из односторонних пентамино
Если дополнить набор пентамино зеркальными копиями фигур, не совпадающих со своими отражениями (F, L, P, N, Y и Z), то из полного набора в 18 односторонних пентамино можно сложить прямоугольники площадью 90 единичных квадратов (при этом фигуры не разрешается переворачивать). Задача о составлении прямоугольника 3 × 30 имеет 46 решений, 5 × 18 — более 600 тыс. решений, 6 × 15 — более 2 млн решений и 9 × 10 — более 10 млн решений [3] .
Укладка фигур с отверстиями
В какой-то степени более простую (более симметричную) задачу, для квадрата 8×8 с отверстием в центре 2×2, решил еще в 1958 году Дана Скотт [4] (аспирант-математик Принстона). Для этого случая существует 65 решений. Алгоритм Скотта был одним из первых применений компьютерной программы поиска с возвратом.
Другой вариант этой головоломки — выкладывание квадрата 8×8 с 4 отверстиями в произвольно заданных местах. Большинство таких задач имеют решение. Исключением являются случаи с размещением двух пар отверстий вблизи двух углов доски так, чтобы в каждый угол можно было поместить только P-пентамино, или всех четырёх отверстий вблизи одного угла так, что при любом возможном заполнении угловой клетки (с помощью U- или T-пентамино) от доски отсекается ещё одна клетка (см. рисунок).
Для решения этих задач эффективные алгоритмы описал, например, Дональд Кнут [5] [6] . На современном компьютере подобные головоломки решаются за считанные секунды.
Укладка фигур животных, предметов и техники
Из головоломки можно выкладывать животных, птиц и рыб, а так же растения, различные предметы и технику. Используются при этом как все 12 элементов пентамино, так и их часть.

Эта задача была предложена профессором Калифорнийского университета Р.М.Робинсоном. Выбрав одну из 12 фигур пентамино, необходимо построить из каких-либо 9 из 11 оставшихся пентамино фигуру, подобную выбранной, но в 3 раза большей длины и ширины. Решение существует для любого из 12 пентамино, причём не единственное (от 15 решений для Х до 497 для Р) [3] . Существует вариант этой задачи, в котором для построения утроенной фигуры разрешается использовать также и саму исходную фигуру. В этом случае число решений от 20 для Х до 9144 для Р-пентамино [7] .
Представленное на рисунке решение [8] , найденное А.ван де Ветерингом, обладает интересным свойством: каждое пентамино используется для утроения девяти из остальных, по одному разу в каждой. Таким образом, из 9 комплектов исходных фигур пентамино можно одновременно сложить все 12 утроенных пентамино.
Пентамино может использоваться также как настольная игра для двух игроков [9] . Для игры необходима шахматная доска 8×8 и набор фигур пентамино, клетки которых имеют одинаковый размер с клетками доски. В начале игры доска пуста. Игроки поочерёдно выставляют на доску по одной фигуре, закрывая 5 свободных клеток доски. Все выставленные фигуры остаются на месте до конца партии (не снимаются с доски и не передвигаются). Проигравшим считается игрок, который первым не сможет сделать хода (либо из-за того, что ни одна из оставшихся фигур не умещается на свободных участках доски, либо потому, что все 12 фигур уже выставлены на доску).
Анализ игры достаточно сложен (так, в начале имеется даже больше возможных первых ходов, чем в шахматах). Голомб предложил следующую стратегию: стремиться разбить свободное место на доске на два равновеликих участка (и помешать сопернику сделать это). После этого на каждый ход соперника на одном из участков следует отвечать ходом на другом.
Пример партии в пентамино показан на рисунке. Нумерация ходов сквозная (нечётные номера ходов принадлежат первому игроку, чётные — второму). Первоначально игроки делают ходы в центре доски (ходы 1—3), не позволяя друг другу разбить доску на равновеликие участки. Но затем второй игрок делает неудачный ход (4), позволяющий сопернику разбить свободное место на два участка по 16 клеток (ход 5). (В этом примере свободные участки не только равны по площади, но и совпадают по форме — симметричны относительно диагонали доски, но для стратегии это, разумеется, не обязательно.) Далее на ход второго игрока (6) на одном из этих участков первый игрок отвечает ходом на другом (7) и выигрывает. Хотя на доске ещё есть три свободных участка в пять и более клеток, но все подходящие фигуры (I, P, U) уже использованы.
Варианты настольной игры
Пентамино с заранее выбранными фигурами
В этом варианте игры игроки сначала по очереди выбирают по одной фигуре, пока все фигуры не будут распределены между ними. Далее игра проходит по правилам обычного пентамино, с той разницей, что каждому из игроков разрешается ходить только теми фигурами, которые он выбрал. Взявший последнюю фигуру делает первый ход.
Другие варианты
Из всех пентамино самой долгой эволюцией обладает R-пентамино. Эволюция этого пентамино становится тривиальной лишь спустя 1103 поколения [10] [11] . После 1103 поколений развития R-пентамино популяция состоит из 25 объектов: 8 блоков, 6 планеров, 4 ульев, 4 мигалок, 1 лодки, 1 каравая и 1 корабля [10] [12] .
Пентомина или пентамин геометрическая фигура из 5 квадратов , соединенных одной из своих сторон, это частный случай Полимина .
Резюме
Описание
- L, N, P, F и Y могут давать 8 форм: 4 путем вращения и 4 путем зеркального отображения.
- Z дает 4 формы: 2 при вращении и 2 при зеркальном отображении.
- T, V, U и W дают 4 формы за один оборот.
- Рожаю 2 формы по очереди.
- X может дать начало только одной форме.
Например, восемь возможных конфигураций Y:
Прямоугольники мощения
Классическая головоломка с пентамино состоит в том, чтобы вымостить прямоугольную поверхность без отверстий и перекрытий. Каждое пентамино, числом 12, содержит 5 квадратов. В результате прямоугольник должен иметь площадь 60 квадратов; поэтому единственно возможные размеры - 6 × 10, 5 × 12, 4 × 15 и 3 × 20. Самым целеустремленным игрокам удается выполнить их вручную за несколько часов.
Более сложная задача - подсчитать общее количество возможных решений. Обычно это решается с помощью алгоритма перебора.
Джон Г. Флетчер впервые решил случай 6 × 10 в 1965 году: существует ровно 2339 решений, исключая тривиальные варианты (вращения и отражения прямоугольника), но включая вращения и отражения целого прямоугольника. Прямоугольник 5 × 12 имеет 1010 решений, прямоугольник 4 × 15 имеет 368 решений, а прямоугольник 3 × 20 имеет только 2 решения.
Гораздо более простая головоломка, поскольку она более симметрична, - это квадрат 8 × 8, в центре которого есть отверстие 2 × 2. Дана С. Скотт решила ее в 1958 году, насчитав 65 решений. Его алгоритм является одним из первых, в котором применяется отслеживание с возвратом .
С годами появились и другие алгоритмы. Дональд Кнут , знаковая фигура в ИТ, разработал особенно эффективный вариант. Благодаря ему современный компьютер может найти все решения всего за несколько секунд.
Другие вопросы
Помимо шахматной доски с центральным отверстием, упомянутой в предыдущем абзаце, существует множество других проблем.
На шахматной доске четыре лунки могут быть распределены по-разному (например, по четырем углам).
Скотный двор состоит сделать прямоугольник , содержащий прямоугольное отверстие. Следовательно, это прямоугольник поверхности (60 + n), где n - это площадь двора. Самым маленьким является прямоугольник 7 × 9 и 3 × 1 ярд. Казалось бы, самый большой - прямоугольник 8 × 11 и 4 × 7 ярдов.
Мы также можем сделать прямоугольник с отверстием в форме пентамино.
Тройное воспроизведение: воспроизвести (всего 9 штук) масштаб 3 пентамино без использования увеличенного фрагмента.
| Пентамино | F | я | L | НЕТ | п | Т | U | V | W | Икс | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Решение | 125 | 19 | 113 | 68 | четыреста девяносто семь | 106 | 48 | 63 | 91 | 15 | 86 | 131 |
Наконец, мы можем перейти к верхнему измерению с пентакубами, пентамино, имеющими толщину 1. Затем мы попытаемся расположить их в виде параллелепипеда 3 × 4 × 5 (3940 вариантов), в параллелепипеде 2 × 3 × 10 ( 12 вариантов), в параллелепипеде 2x5x6 (264 возможности) или в пентамино в масштабе 2x2x3.
В настольную игру Pentominoes используется сетка 8 × 8. Игроки, двое или трое, по очереди кладут пентамино так, чтобы не было перекрытия, и каждая плитка используется только один раз. Победителем становится последний игрок, разместивший плитку на сетке. Есть стратегии, которые гарантируют победу игроку, который ходит первым.
Вариант Blokus разыгрывается на сетке 20 × 20 с участием от двух до четырех игроков. Чтобы поместить пентамино, он должен касаться пентамино того же цвета одним углом и не перекрывать другие пентамино.
Пентамино - это основа различных одиночных игр, в которых требуется мощение поверхности или решение головоломки (например, КАТАМИНО). Детали могут быть сделаны из дерева или других материалов или дематериализованы в различных компьютерных программах и онлайн-играх.
Анекдоты
Если рассматривать вращения фигур на 90°, то существуют следующие категории симметрии:
- L, N, P, F и Y могут быть ориентированы 8 способами каждая: 4 поворотами и ещё 4 зеркальными отображениями.
- Z может быть ориентирована 4 способами: 2 — поворотами, 2 — зеркальными отображениями.
- T, V, U и W могут быть ориентированы поворотами 4 способами каждая.
- I может быть ориентирована поворотами 2 способами.
- X может быть ориентирована единственным способом.
Отсюда число фиксированных пентамино равно 5 × 8 + (1 + 4) × 4 + 2 + 1 = 63.
Например, вот восемь возможных способов ориентации пентамино L, F, P, N и Y:
Укладка прямоугольников
Самая распространённая задача в пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20. Каждую из этих головоломок можно решить вручную, но более сложной задачей является подсчёт общего числа возможных решений в каждом случае (очевидно, прямоугольники 2 × 30 и 1 × 60 составить из пентамино невозможно, поскольку многие фигуры в них просто не помещаются по ширине).
Для случая 6 × 10 эту задачу впервые решил в 1965 году Джон Флетчер [2] . Существует 2339 различных укладок пентамино в прямоугольник 6×10, не считая поворотов и отражений целого прямоугольника, но считая повороты и отражения его частей (иногда внутри прямоугольника образуется симметричная комбинация фигур, поворачивая которую, можно получить дополнительные решения; для прямоугольника 3×20, приведённого на рисунке, второе решение можно получить поворотом блока из 7 фигур, или, иначе говоря, если поменять местами четыре фигуры, крайние слева, и одну крайнюю справа).
Для прямоугольника 5 × 12 существует 1010 решений, 4 × 15 — 368 решений, 3 × 20 — всего 2 решения (отличающихся вышеописанным поворотом). В частности, существует 16 способов сложить два прямоугольника 5 × 6, из которых можно составить как прямоугольник 6 × 10, так и 5 × 12.
Укладка прямоугольников из односторонних пентамино
Если дополнить набор пентамино зеркальными копиями фигур, не совпадающих со своими отражениями (F, L, P, N, Y и Z), то из полного набора в 18 односторонних пентамино можно сложить прямоугольники площадью 90 единичных квадратов (при этом фигуры не разрешается переворачивать). Задача о составлении прямоугольника 3 × 30 имеет 46 решений, 5 × 18 — более 600 тыс. решений, 6 × 15 — более 2 млн решений и 9 × 10 — более 10 млн решений [3] .
Укладка фигур с отверстиями
В какой-то степени более простую (более симметричную) задачу, для квадрата 8×8 с отверстием в центре 2×2, решил еще в 1958 году Дана Скотт [4] (аспирант-математик Принстона). Для этого случая существует 65 решений. Алгоритм Скотта был одним из первых применений компьютерной программы поиска с возвратом.
Другой вариант этой головоломки — выкладывание квадрата 8×8 с 4 отверстиями в произвольно заданных местах. Большинство таких задач имеют решение. Исключением являются случаи с размещением двух пар отверстий вблизи двух углов доски так, чтобы в каждый угол можно было поместить только P-пентамино, или всех четырёх отверстий вблизи одного угла так, что при любом возможном заполнении угловой клетки (с помощью U- или T-пентамино) от доски отсекается ещё одна клетка (см. рисунок).
Для решения этих задач эффективные алгоритмы описал, например, Дональд Кнут [5] [6] . На современном компьютере подобные головоломки решаются за считанные секунды.
Укладка фигур животных, предметов и техники
Из головоломки можно выкладывать животных, птиц и рыб, а так же растения, различные предметы и технику. Используются при этом как все 12 элементов пентамино, так и их часть.

Эта задача была предложена профессором Калифорнийского университета Р.М.Робинсоном. Выбрав одну из 12 фигур пентамино, необходимо построить из каких-либо 9 из 11 оставшихся пентамино фигуру, подобную выбранной, но в 3 раза большей длины и ширины. Решение существует для любого из 12 пентамино, причём не единственное (от 15 решений для Х до 497 для Р) [3] . Существует вариант этой задачи, в котором для построения утроенной фигуры разрешается использовать также и саму исходную фигуру. В этом случае число решений от 20 для Х до 9144 для Р-пентамино [7] .
Представленное на рисунке решение [8] , найденное А.ван де Ветерингом, обладает интересным свойством: каждое пентамино используется для утроения девяти из остальных, по одному разу в каждой. Таким образом, из 9 комплектов исходных фигур пентамино можно одновременно сложить все 12 утроенных пентамино.
Пентамино может использоваться также как настольная игра для двух игроков [9] . Для игры необходима шахматная доска 8×8 и набор фигур пентамино, клетки которых имеют одинаковый размер с клетками доски. В начале игры доска пуста. Игроки поочерёдно выставляют на доску по одной фигуре, закрывая 5 свободных клеток доски. Все выставленные фигуры остаются на месте до конца партии (не снимаются с доски и не передвигаются). Проигравшим считается игрок, который первым не сможет сделать хода (либо из-за того, что ни одна из оставшихся фигур не умещается на свободных участках доски, либо потому, что все 12 фигур уже выставлены на доску).
Анализ игры достаточно сложен (так, в начале имеется даже больше возможных первых ходов, чем в шахматах). Голомб предложил следующую стратегию: стремиться разбить свободное место на доске на два равновеликих участка (и помешать сопернику сделать это). После этого на каждый ход соперника на одном из участков следует отвечать ходом на другом.
Пример партии в пентамино показан на рисунке. Нумерация ходов сквозная (нечётные номера ходов принадлежат первому игроку, чётные — второму). Первоначально игроки делают ходы в центре доски (ходы 1—3), не позволяя друг другу разбить доску на равновеликие участки. Но затем второй игрок делает неудачный ход (4), позволяющий сопернику разбить свободное место на два участка по 16 клеток (ход 5). (В этом примере свободные участки не только равны по площади, но и совпадают по форме — симметричны относительно диагонали доски, но для стратегии это, разумеется, не обязательно.) Далее на ход второго игрока (6) на одном из этих участков первый игрок отвечает ходом на другом (7) и выигрывает. Хотя на доске ещё есть три свободных участка в пять и более клеток, но все подходящие фигуры (I, P, U) уже использованы.
Варианты настольной игры
Пентамино с заранее выбранными фигурами
В этом варианте игры игроки сначала по очереди выбирают по одной фигуре, пока все фигуры не будут распределены между ними. Далее игра проходит по правилам обычного пентамино, с той разницей, что каждому из игроков разрешается ходить только теми фигурами, которые он выбрал. Взявший последнюю фигуру делает первый ход.
Другие варианты
Из всех пентамино самой долгой эволюцией обладает R-пентамино. Эволюция этого пентамино становится тривиальной лишь спустя 1103 поколения [10] [11] . После 1103 поколений развития R-пентамино популяция состоит из 25 объектов: 8 блоков, 6 планеров, 4 ульев, 4 мигалок, 1 лодки, 1 каравая и 1 корабля [10] [12] .
Из трёх различных фигур пентамино составьте прямоугольник 3x5. Сколько различных решений имеет задача?
Решение 1
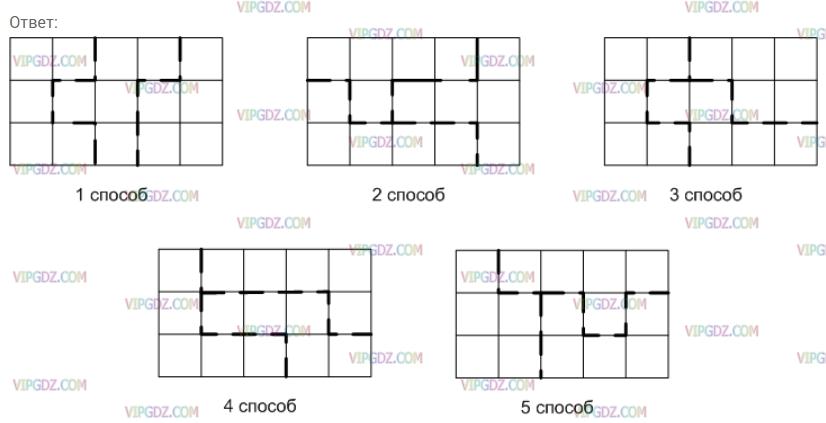
Решение 2
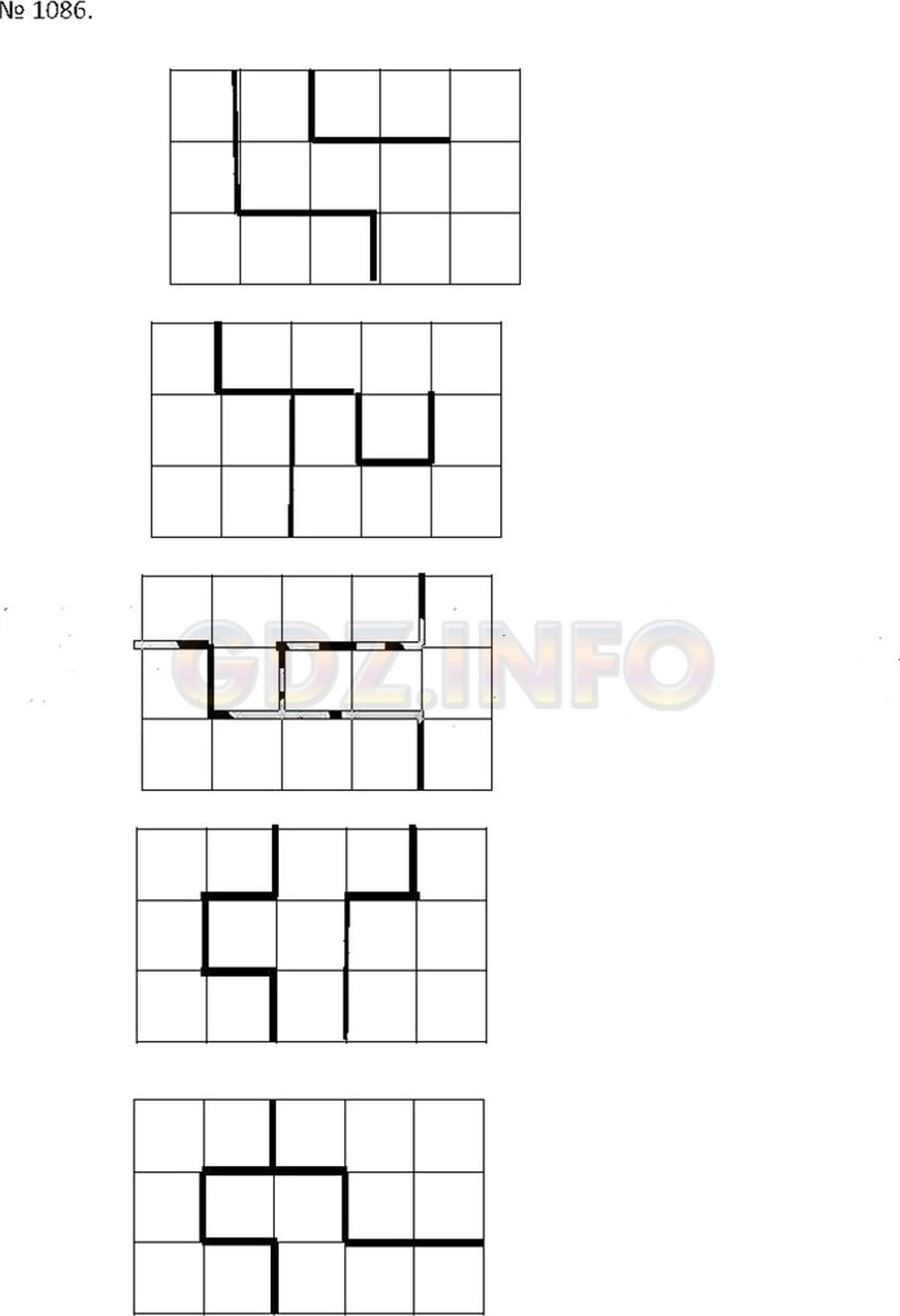
Поиск в решебнике
Популярные решебники
Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. - 2013г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015г.
Читайте также:

