Как сделать пчелиные соты в 3д макс
Добавил пользователь Дмитрий К. Обновлено: 05.10.2024

Как сделать

Что сделать

Команда

Пчелиные соты Как сделать пчелиные соты в Майнкрафт | Скриншот 1

Пчелиные соты Как сделать пчелиные соты в Майнкрафт | Скриншот 2

Как сделать

Что сделать

Команда
Чтобы получить соты, нужно иметь ножницы и заполненный мёдом улей. Нажав правой кнопкой мыши на улей (с ножницами в руке) игрок получит 3 единицы пчелиных сот. Соты можно объединить в блок в инвентаре.
- Синонимы: Honeycomb
- Версии Майнкрафт: 1.17 / 1.16.5 / 1.16.4 / 1.16.3 / 1.16.2 / 1.16.1 / 1.16
- ID: honeycomb

Как сделать пчелиные соты
Здесь указано, как сделать пчелиные соты в Майнкрафте. В рецепте крафта указываются необходимые ингредиенты и их расположение в Minecraft.

Как сделать

Что сделать

Видео

Скриншоты

Команда

Чтобы получить соты, нужно иметь ножницы и заполненный мёдом улей. Нажав правой кнопкой мыши на улей (с ножницами в руке) игрок получит 3 единицы пчелиных сот. Соты можно объединить в блок в инвентаре.
- Версии Майнкрафт: 1.18.1 / 1.18 / 1.18 / 1.18 / 1.18 / 1.17.1 / 1.17
- COMMAND: honeycomb
![]()
Как сделать пчелиные соты
Есть несколько рецептов, как сделать пчелиные соты в Майнкрафт. Ниже вы можете посмотреть описание всех рецептов: картинки с ингредиентами и пошаговые инструкции, как скрафтить пчелиные соты в игре Minecraft.
Сертификат и скидка на обучение каждому участнику

Глазковский филиал имени Героя Советского Союза Н. Н. Шерстова МБОУ Кочетовская СОШ Мичуринского района
Открытая научно – практическая конференция
Секция экономико – математических наук
Исследовательская работа по математике
«Пчелиные соты – это математический
Выполнила ученица 11 Б класса
Зайцева Любовь
Научный руководитель:
учитель математики первой категории
Скрылева Нина Васильевна
Глазок - 2012
Глава 1.Назначение пчелиных сот. 6
Глава 2.Общая конструкция пчелиных сот. 9
Глава 3.Математический анализ строения пчелиных сот. 11
3.1. Заполнение плоскости правильными многоугольниками
без просветов. 11
3.2. Сравнение периметров правильных многоугольников. 13
3.3. Сравнение площадей поверхности и
объемов правильной шестиугольной призмы и пчелиной ячейки. 14
Глава 4. Экономическая выгода пчел при построении сот. 17
Глава 5. Применение принципа пчелиных сот в жизни человека. 18
« Только глупец может рассматривать
удивительное строение сот,
столь совершенно приноровленного к известным
Пчелы - удивительные творения природы. Жизнь и деятельность пчел всегда привлекала внимание человека, исследователя своей изумительной красотой, изяществом, трудолюбием и распределением обязанностей между собой. Ведь только пчелы на практике решили задачу строительства ячейки для размещения возможно большего количества меда и экономии воска. Совершенство природы до сих пор не устает удивлять человека, а математика – это уникальное средство познания красоты и природы.
Актуальность исследования заключается в объяснении теоретического вывода о том, что в пчелиных ячейках, имеющих форму шестигранника, в основании которой лежит трехгранный угол, наибольшее количество меда при максимальной экономии воска и применения данных выводов в жизни, которые будут достигнуты в результате выполнения работы.
Новизна исследования заключается в использовании математических подходов и методов исследования при выполнении данной работы, получения новых знаний, являющихся результатом исследовательской работы.
Задачи исследования:
1)Изучить литературу по данному вопросу.
2)Познакомиться с геометрическим принципом построения пчелиных сот.
3)Выявить закономерности построения пчелиной ячейки.
4)Провести математический анализ строения пчелиной ячейки.
5)Проанализировать экономическую выгоду построения соты.
6)Рассмотреть использование геометрических закономерностей построения пчелиных сот в различных областях и в жизни человека.
7)Сделать выводы о геометрических способностях пчел.
Объект исследования: пчелиные соты, структурный элемент пчелиных сот – пчелиная ячейка.
Предмет исследования: геометрические принципы построения пчелиных сот.
Методы исследования: математический анализ, моделирование, сравнительный анализ.
Теоретическая значимость работы определяется тем, что мы рассматриваем новый вид многогранника – шестиугольную призму, нижним основанием которого является трехгранный угол, гранями которого являются ромбы. Данный вид многогранника не изучается в школьном курсе математики.
Практическая значимость работы показывает, что можно использовать новый вид многогранника в качестве сосуда с наименьшей площадью поверхности и наибольшим объемом, а также использование геометрических закономерностей построения пчелиных сот в различных областях науки и жизни человека.
Глава 1.Назначение пчелиных сот.
Очень удивителен и метод, используемый в строительстве сот: пчелы начинают строить соты одновременно с 2-3 разных точек, и возводят их в 2-3 ряда. Таким образом, большой рой пчел, начиная с разных точек, делает шестиугольники одинаковых размеров, соединяет их и в завершении работы встречается в середине. Шестиугольники соединены настолько профессионально, что внешне невозможно увидеть следов воссоединения сот.
Только пчелы снабжены особыми восковыми железами, которые расположены на четырех последних брюшных полукольцах; через многочисленные отверстия выделяются восковые пластинки. Сто таких пластинок весят всего 25 мг, а в килограмме воска их насчитывается 4 млн. Из этих крошечных восковых пластинок в темноте пчелы строят изумительной красоты восковые закрома для меда и цветочной пыльцы, прочные и уютные кельи для развития потомства. На одну пчелиную ячейку пчелы расходуют 13 мг воска, или 50 пластинок, а на трутневую (мужские особи) - 30 мг воска, или 120 пластинок. Каждый сот состоит из двух рядов шестигранных восковых ячеек, имеющих особую перегородку (средостение), служащую донышком для этих ячеек. Такой сот весит всего лишь 150 г. (Фото 5)
Строительство сот и сбор нектара протекают одновременно и, когда прекращается одно, останавливается и другое. Как только взяток (наличие нектара на цветах) ослабевает настолько, что потребление нектара или меда превышает его поступление, пчелы прекращают строить новые соты, даже если большая часть жилища не застроена.
Вывод: соты предназначены для хранения меда, выращивания расплода и являются гнездом пчелиной семьи.
Глава 2. Общая конструкция пчелиных сот.
Конструкция сот уникальна и совершенна во всех отношениях. Она обеспечивает максимальное использование пространства, общую экономичность и высокую прочность всего сооружения. Пчелы начинают строительство сот со дна ячейки шестиугольной формы, к которой затем с обеих сторон постепенно надстраиваются грани. Добавляя дно ячеек, друг к другу вниз и в стороны и надстраивая по мере увеличения площади основания ячейки, пчелы создают восковое сооружение с общим вертикальным основанием, имеющим шестигранные ячейки с двух сторон.
На этом математические секреты пчел не заканчиваются. Нам стало интересно дальше исследовать строение пчелиных сот. Соты в улье свешиваются сверху вниз наподобие занавесок: пчелы прикрепляют их к потолку смесью воска и пчелиного клея (прополиса). Ячейки уложены в пласты и соприкасаются общими донышками. Но самое неожиданное, мы увидели, что донышки ячеек не плоские, а представляют собой части трехгранных углов, гранями которых являются равные ромбы. На рис. 3 мною изображена пчелиная ячейка в общем виде, а на рис. 4 - ее проекции: вид сверху, спереди и сбоку.
Нам захотелось построить развертку многогранника SABCDEFF MB LD K (одна ячейка сот). Но прежде чем начать построение развертки, нам необходимо рассмотреть чисто геометрически, как получается ячейка.
Сначала мы построим изображение правильной шестиугольной призмы ABCDEFA B C Д E F . Проведём диагонали F B, BД, F Д верхнего основания призмы и на оси призмы ОО возьмём некоторую точку S (рис. 5). Через прямые F B , B Д , F Д и точку S проведём три плоскости, которые отсекают от призмы три равные треугольные пирамиды M B F A , B LD C , D KFE . Получившийся многогранник SABCDEFF MB LD K и является пчелиной ячейкой. Поскольку боковая поверхность многогранника представляет собой шесть равных между собой трапеций, то для получения развертки мы построим эти трапеции. Размеры возьмём такие же, как на рис. 4, причем отрезок MS на рис. 4, а - это диагональ ромба в верхней части ячейки. Построим отрезок АА' = АВ + ВС + CD + DE + EF + FA (рис.6). На продолжении ребра CL от точки L отложу отрезок LS и из точки L проведём окружность радиусом, равным, например, отрезку В L. После этого построим середину отрезка LS, проведём через нее перпендикулярную к нему прямую, которая пересекает дугу окружности в двух вершинах ромба. Два других ромба строим следующим образом: из вершины ромба D′ проводим окружность радиусом, равным стороне построенного ромба, а из вершины S - окружность, радиус которой равен диагонали ромба. Эти окружности в пересечении дают еще одну вершину ромба. Развертка пчелиной ячейки показана на рис. 6. А на рис. 7 можно увидеть, как соприкасаются ячейки в улье; их общая часть является ромбом.
В качестве строительных ориентиров по пространственному размещению сот пчелы используют магнитное поле земли, направление и силу магнитных полей которого они могут воспринимать и запоминать. Поэтому роевые пчелы, строящие соты без вощины, дают им направление такое, какое имели соты в их бывшей семье.
Следовательно, пчелиные соты представляют собой новый вид многогранника - шестиугольную призму, нижним основанием которого является трехгранный угол, гранями которого являются ромбы.
Глава 3. Математический анализ строения пчелиных сот.
3.1. Доказательство заполнения плоскости правильными многоугольниками без просветов.
Выполняя несложные расчеты, мы убедилась, что такими многоугольниками могут быть только правильные треугольники, квадраты или правильные шестиугольники. Действительно, сумма внутренних углов выпуклого n - угольника равна ( n - 2)180 , где n - число сторон многоугольника. Сумма углов правильных n-угольников, сходящихся в одной вершине паркета, равна 360 .
или , где k – число углов, сходящихся в одной вершине.
Если n = 3, то к = 6, т. е. в одной вершине паркета могут сходиться 6 правильных треугольников (рис. 8);
если n = 4, то к= 4, т. е. в одной вершине паркета могут сходиться 4 квадрата (рис. 9);
если n = 5, то к = 3,3, т. е. не существует паркета из правильных пятиугольников;
если n = 6, то к = 3, т. е. в одной вершине паркета могут сходиться 3 правильных шестиугольника (рис. 10);
если n = 7, то к = 2,8, т. е. не существует паркета из правильных семиугольников. И так далее.
Теперь мы рассуждаем таким образом: , так как
внутренний угол правильного многоугольника меньше 180 ,значит,
По смыслу задачи значения n , k и могут быть только целыми, поэтому 4 делится нацело на n - 2. Следовательно, n = 3, 4, 6.
Итак, мы выяснили, что заполнить плоскость без пропусков можно, используя или правильные треугольники, или квадраты, или правильные шестиугольники.

МОУСОШ№2 имени Героя Советского Союза А.В.Ляпидевского гЕйска МО Ейский район.

Дроздова Яна , ученица 8Б класса
Актуальность работы. Умение применять знания школьного курса геометрии в жизни, что способствует расширению кругозора и уделение более пристального внимания школьному материалу.
Цель работы. Для полного раскрытия темы ставится следующая цель: умение решать задачи практического характера, с применением приобретенных знаний в школе; расширение кругозора в ходе исследования, а так же показать связь математики с жизнью и эффективность математики.
Постановка задач. Достижение поставленной цели возможно путем рассмотрения следующих задач: 1) доказательство составления паркета из правильных многоугольников: 2) выявления правильного многоугольника с наименьшим периметром; 3) применение геометрических построений при рассмотрении пчелиных ячеек сот;
4) выявление наименьшей площади поверхности многогранника.
Объект исследования. Объектом изучения работы является пчела, ее соты.
Содержание работы.
- начало исследования – знакомство с интересной задачей про пчел, а так же наблюдение
за строительством пчелиных сот;
- причины, по которым строительство ячеек сот соответствует правильному
- принцип построения паркетов из правильных многоугольников;
- выявление наименьшего периметра правильного многоугольника с применением формул
нахождения площадей, сторон и периметров этих многоугольников;
- построение одной ячейки с применением геометрических построений и знанием
пространственных тел- многогранников.
- сравнение площадей поверхности многогранников и пчелиной ячейки;
- геометрические способности пчел помогают им экономить время, воск и силы.
Выводы по работе.
В заключении мне бы хотелось сказать, что геометрический подход к природным явлениям позволяет увидеть внутренний мир, гармонию, структуру этого явления.
А исследования, проведенные в ходе работы, знакомят и сближают нас с гармонией
и целесообразностью природы.
1. Вступление.
Связывая природу, математику, и искусство, можно убедиться
в том, что для тех, кто стоял у истоков искусства, природа и
человек были образцами для подражания. Есть такие творения
природы, которых человек порой не замечает___________________стр2.
2. Основная часть.
1) Сеть правильных шестиугольников_______________________стр3.
а) формулировка задачи о составлении паркета____________стр3.
б) доказательство задачи_______________________________стр4.
в) составление паркета из правильного треугольника,
квадрата и правильного шестиугольника_______________стр5.
3) Расчетливая геометрия:
а) доказательство того, что периметр правильного
шестиугольника наименьший из периметров
остальных правильных многоугольников ______________стр6.
б) построение ячейки пчелиных сот, и их проекции_________стр8.
в) доказательство того, что площадь поверхности
пчелиной ячейки наименьшая из поверхностей
других многогранников, имеющих одинаковый
3. Заключение.
Всесторонняя эффективность математики___________________стр11.
4. Список литературы ____________________________________стр12
Пчёлы – удивительные творения природы. Геометрические способности пчёл проявляются при построении сот. Если разрезать пчелиные соты плоскостью, перпендикулярной их рёбрам, то будет видна сеть правильных шестиугольников, уложенных в виде паркета.
В учебнике за пятый класс есть очень интересная задача о пчёлах. А так как мы сами разводим пчёл, то я решила обратить на неё наиболее пристальное внимание.
Чтобы собрать 100 грамм мёда, пчела доставляет в улей 16 тысяч нош нектара. Вопрос задачи: какова масса одной ноши?
100 : 16000=0,00625 (г) -масса одной ноши.
Ответ: 0,00625 грамм.
А умещает пчела свою ношу на своей ножке в мешочке.
Решив эту задачу, можно сделать следующий вывод: пчела очень трудолюбива, прикладывает огромные усилия для того чтобы, собрать мёд.
2.Основная часть.
Теперь попытаемся ответить на вопрос: «Почему пчелы строят соты именно так, почему они предпочли сеть правильных шестиугольников, а не правильных треугольников или квадратов?
Чтобы ответить на этот вопрос, необходимо предварительно выяснить, какими правильными многоугольниками можно заполнить плоскость так, чтобы не было пропусков, то есть уложить их в виде паркета.
Выполняя несложные расчёты, убеждаемся, что такими многоугольниками могут быть только квадраты, правильные треугольники и правильные шестиугольники.
Квадрат правильный треугольник правильный шестиугольник.
Действительно, сумма внутренних углов выпуклого n -угольника равна
( n -2)·180º, где n -число сторон многоугольника. Сумма углов правильных n -угольников, сходящихся в одной вершине паркета, равна 360º. Тогда приравняв сумму внутренних углов к числу 360, мы получим следующее равенство: .
Решаем это уравнение относительно числа к, тогда получим:
где k - число углов, сходящихся в одной вершине паркета.
Рассмотрим некоторые правильные многоугольники.
1). Возьмём треугольник с количеством сторон равным трём.
Тогда, если n =3, то k =6. А это значит, что в одной вершине паркета могут сходиться шесть правильных шестиугольников;
2). Возьмём квадрат с количеством сторон равным четырём.
Тогда, если n =4, то k =4, то есть в одной вершине паркета могут сходиться четыре квадрата.
3). Возьмём пятиугольник с количеством сторон равным пяти.
Если n =5, то k =3,3. А так как k получили не целое число, то не существует паркета из правильных пятиугольников.
4). Возьмём шестиугольник с количеством сторон равным шести.
Тогда, если n =6, то k =3, то есть в одной вершине паркета могут сходиться три правильных шестиугольника;
5). Возьмём семиугольник с количеством сторон равным семи.
Если n =7, то k =2,8. А так как k получили не целое число, то не существует паркета из правильных семиугольников. И так можно продолжать дальше.
Теперь рассуждаем следующим образом: ,так как внутренний угол правильного многоугольника меньше 180º;
По смыслу задачи значения n , k и могут быть только целыми , поэтому 4 делится нацело на ( n -2). Отсюда n = 3,4,6.
Итак, мы выяснили, что заполнить плоскость без пропусков можно, используя или правильные треугольники, или квадраты, или правильные шестиугольники. Только ими можно уложить паркет без пропусков.
1) из правильных треугольников
2) из правильных четырехугольников
3) из правильных шестиугольников
Для того чтобы выяснить, почему пчела строит соты, перпендикулярное сечение которых есть правильный шестиугольник, а не правильный треугольник или квадрат, рассмотрим вспомогательную задачу.
Задача №3: Даны три равновеликие друг другу фигуры – правильный треугольник, квадрат, правильный шестиугольник. Какая из данных фигур имеет наименьший периметр?
Дано : правильный треугольник, квадрат, правильный треугольник. S – из правильных многоугольников. . S =4 см 2
Найти: периметр каждого правильного многоугольника.
Пусть S – площадь каждой из данных фигур.
а 3 , а 4 , а 6 - стороны соответствующих многоугольников.
S =4 см 2 .
1). Тогда вычислим площадь треугольника по формуле:
Подставив данные правильного треугольника в эту формулу, получим:
2). Площадь квадрата вычислим по формуле:
3). Площадь правильного шестиугольника состоит из шести площадей правильного треугольника. Тогда получим:
Теперь нетрудно вычислить периметр каждой фигуры, зная её площадь.
Сначала выразим сторону каждого многоугольника через его площадь, затем найдем периметр этого многоугольника:
Подставив в формулу значение площади, равное 4 см 2 , получим, что
Аналогично выразим сторону квадрата через его площадь и найдем периметр квадрата при заданном значении его площади:
Осталось выразить сторону правильного шестиугольника через его площадь и найти периметр:
Для сравнения периметров фигур найдём их отношение:
Мы видим, что из трёх правильных многоугольников с одинаковой площадью наименьший периметр имеет правильный шестиугольник. Стало быть, выбрав правильный шестиугольник, мудрые пчёлы экономят воск и время для построения сот.
Надо сказать, что на этом математические секреты пчёл не заканчиваются. Интересно и дальше исследовать строение пчелиных сот.
Соты в улье свешиваются сверху вниз наподобие занавесок:
пчёлы прикрепляют их к потолку смесью воска или пчелиного клея (прополиса). Ячейки уложены в пласты и соприкасаются общими донышками.
Но донышки ячеек не плоские, а представляют собой части трёхгранных углов, гранями которых являются равные ромбы.
На рисунке 1 изображена пчелиная ячейка в общем виде, а на рисунке 2 – её проекции: вид сверху, вид спереди и вид сбоку.
Попробуем построить развёртку многогранника (одна ячейка сот). Но прежде чем начать построение сот развёрстки, необходимо рассмотреть чисто геометрически, как получается ячейка.
Сначала построим изображение правильной шестиугольной призмы. Проведём диагонали верхнего основания призмы и на оси призмы возьмём некоторую точку S . Через прямые и точку S проводим три плоскости, которые отсекают от призмы три равные треугольные пирамиды . Получившийся многогранник и является пчелиной ячейкой.
Поскольку боковая поверхность многогранника представляет собой шесть равных между собой трапеций, то для получения развёртки построим эти трапеции. Их размеры возьмём такими же, как на рисунке 2 , причём отрезок MS на рисунке 2, a -это диагональ ромба в верхней части ячейки.
Построим отрезок AA ´= AB + BC + CD + DE + EF + FA (рисунок 4). На продолжении ребра CL от точки L отложим отрезок LS и из точки L проведём окружность радиусом, равным, например, отрезку. После этого построим середину отрезка LS , проведём через неё перпендикулярную к нему
прямую, которая пересекает дугу окружности в двух вершинах ромба. Два других ромба строим следующим образом: из вершины ромба проводим окружность радиусом, равным стороне построенного ромба, а из вершины S – окружность, радиус которой равен диагонали ромба. Эти окружности в пересечении дают ещё одну вершину ромба. Остальные построения очень просты. Развёртка пчелиной ячейки показана на рисунке 4.
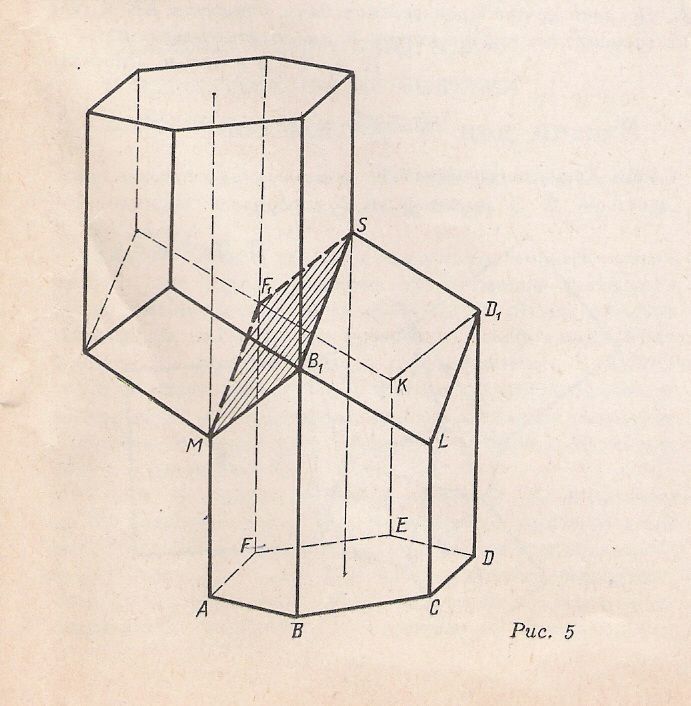
. А на рисунке 5 можно увидеть, как соприкасаются ячейки в улье; их общая часть является ромбом.
Когда говорят о пчёлах, то чаще всего демонстрируют рисунок 6 , показывающий соты в разрезе плоскостью, перпендикулярной боковому ребру и пересекающей все соты по правильным шестиугольникам.
Если продолжить одну из боковых граней ячейки так, чтобы она пересекала остальные соты, то сечение будет таким, как показано на рисунке 7.
Небезынтересен вопрос, почему пчёлы строят донышки своих ячеек в форме части трёхгранного угла, в качестве граней которого служат ромбы. Нельзя ли было поступить проще, сделать дно сот плоским, то есть обычным правильным шестиугольником? Какая же здесь выгода для пчёл?
Вернёмся к ячейке-многограннику на рисунке 3. Объём многогранника
равен объёму правильной шестиугольной призмы. Как нетрудно заметить, объём пирамиды равен утроенному объёму одной из равных пирамид.
Пирамиды и равны (они симметричны относительно точки Т). Мы можем самостоятельно провести доказательство равенства названных пирамид, оно несложно. Итак, объёмы пчелиной ячейки и правильной шестиугольной призмы равны.
Зато площадь ее поверхности меньше площади поверхности шестиугольной призмы.
В итоге необходимо сказать, что пчелиные соты представляют собой пространственный паркет, поскольку заполняют пространство так, что не остаётся просветов.
Так с помощью геометрии и математического анализа мы прикоснулись к тайне математических шедевров из воска, ещё раз убедившись во всесторонней эффективности математики.
4. Список литературы:
Дистанционное обучение педагогов по ФГОС по низким ценам
Вебинары, курсы повышения квалификации, профессиональная переподготовка и профессиональное обучение. Низкие цены. Более 13900 образовательных программ. Диплом госудаственного образца для курсов, переподготовки и профобучения. Сертификат за участие в вебинарах. Бесплатные вебинары. Лицензия.
Читайте также:

