Как сделать каноническое уравнение параболы
Добавил пользователь Дмитрий К. Обновлено: 04.10.2024
Кривая второго порядка - это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах - при вторых степенях одновременно не нули.
или можно встретить следующую форму записи:
К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
если Δ F1 и F2 - фокусы.
с - фокальное расстояние,
Каноническое уравнение эллипса с центром симметрии в начале координат:
2а - большая ось эллипса, 2b - малая ось эллипса.
а - большая полуось эллипса, b - малая полуось эллипса.
Если a = b, то имеем окружность с радиусов R = a = b:
Если центр эллипса находится не в начале координат, а в некоторой точке C(x0;y0), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:
Эксцентриситет - число, равное отношению фокального расстояния к большей полуоси:
Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.
Гипербола - множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
с - фокальное расстояние,
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
Каноническое уравнение гиперболы с центром симметрии в начале координат:
x - действительная ось, y - мнимая ось.
а - действительная полуось, b - мнимая полуось.
Если центр гиперболы находится в некоторой точке C(x0;y0), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:
Эксцентриситет гиперболы - число, равное отношению фокусного расстояния к действительной полуоси.
Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.
Директриса гиперболы - прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.
f1 - правая директриса, f2 - левая директриса.
Порядок построения гиперболы :
1. Строим прямоугольник со сторонами 2a и 2b.
2. Провести асимптоты гиперболы - диагонали построенного прямоугольника.
3. Строим гиперболу с вершинами в точках А1 (-а;0), А 2 (а;0).
Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^=2px\label
$$
при условии \(p > 0\).
Из уравнения \eqref вытекает, что для всех точек параболы \(x \geq 0\). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.
Форма параболы известна из курса средней школы, где она встречается в качестве графика функции \(y=ax^\). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством \(2p=a^\).
Фокусом параболы называется точка \(F\) с координатами \((p/2, 0)\) в канонической системе координат.
Директрисой параболы называется прямая с уравнением \(x=-p/2\) в канонической системе координат (\(PQ\) на рис. 8.11).
Рис. 8.11. Парабола.
Свойства параболы.
Расстояние от точки \(M(x, y)\), лежащей на параболе, до фокуса равно
$$
r=x+\frac
.\label
$$
Вычислим квадрат расстояния от точки \(M(x, y)\) до фокуса по координатам этих точек: \(r^=(x-p/2)^+y^\) и подставим сюда \(y^\) из канонического уравнения параболы. Мы получаем
$$
r^=\left(x-\frac
\right)^+2px=\left(x+\frac
\right)^.\nonumber
$$
Отсюда в силу \(x \geq 0\) следует равенство \eqref.
Заметим, что расстояние от точки \(M\) до директрисы также равно
$$
d=x+\frac
.\nonumber
$$
Следовательно, мы можем сделать следующий вывод.
Для того чтобы точка \(M\) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.
Докажем достаточность. Пусть точка \(M(x, y)\) одинаково удалена от фокуса и от директрисы параболы:
$$
\sqrt<\left(x-\frac
\right)^+y^>=x+\frac
.\nonumber
$$
Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы \eqref. Это заканчивает доказательство.
Параболе приписывается эксцентриситет \(\varepsilon=1\). В силу этого соглашения формула
$$
\frac=\varepsilon\nonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.
Уравнение касательной к параболе.
Выведем уравнение касательной к параболе в точке \(M_(x_, y_)\), лежащей на ней. Пусть \(y_ \neq 0\). Через точку \(M_\) проходит график функции \(y=f(x)\), целиком лежащий на параболе. (Это \(y=\sqrt\) или же \(y=-\sqrt\), смотря по знаку \(y_\).) Для функции \(f(x)\) выполнено тождество \((f(x))^=2px\), дифференцируя которое имеем \(2f(x)f'(x)=2p\). Подставляя \(x=x_\) и \(f(x_)=y_\), находим \(f'(x_)=p/y_\) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_=\frac
$$
Упростим его. Для этого раскроем скобки и вспомним, что \(y_^=2px_\). Теперь уравнение касательной принимает окончательный вид
$$
yy_=p(x+x_).\label
$$
Заметим, что для вершины параболы, которую мы исключили, положив \(y_ \neq 0\), уравнение \eqref превращается в уравнение \(x=0\), то есть в уравнение касательной в вершине. Поэтому уравнение \eqref справедливо для любой точки на параболе.
Касательная к параболе в точке \(M_\) есть биссектриса угла, смежного с углом между отрезком, который соединяет \(M_\) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).
Рассмотрим касательную в точке \(M_(x_, y_)\). Из уравнения \eqref получаем ее направляющий вектор \(\boldsymbol(y_, p)\). Значит, \((\boldsymbol, \boldsymbol_)=y_\) и \(\cos \varphi_=y_/\boldsymbol\). Вектор \(\overrightarrow y_+py_=y_(x_+\frac ).\nonumber Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки (фокуса), и данной прямой (директрисы). По определению | KM |=| MF | , тогда с учетом , получим уравнение . Возведем это равенство в квадрат: Это каноническое уравнение параболы ветвью вправо (рис. 2.8). Очевидно, что x ≥ 0 и каждому x соответствует два значения y , равных по величине и противоположных по знаку, следовательно, парабола симметрична относительно оси 0 x . Эксцентриситет параболы (аналогично эллипсу и гиперболе) определяется формулой: . Можно показать, что парабола ветвью влево (рис. 2.9), имеет уравнение y 2 = – 2 px . Для параболы ветвями вверх ( рис. 2.10 ) или вниз (рис. 2.11 ) уравнения выводятся аналогично уравнению (2.19) и имеют соответственно канонический вид x 2 =2 py и y 2 =2 px. Пример 2.7. Составить уравнение линии, для каждой точки которой ее расстояние до точки A (3;–4) равно расстоянию до прямой y = 2 . Полученное уравнение привести к каноническому виду. Решение. Пусть M ( x ; y ) – текущая точка искомой кривой. Опустим из точки M перпендикуляр MB на прямую y = 2. Тогда точка B имеет координаты ( x ; 2). Так как по условию MA = MB , то Полученное уравнение определяет параболу ветвью вниз и с вершиной в точке O ’ ( 3;–1). Точка A ( 3;–4) является фокусом параболы. Для приведения уравнения к простейшему (каноническому) виду положим x – 3= x ’ , y + 1= y ’ . Тогда в системе координат x ’ 0 ’ y ’ уравнение параболы принимает следующий вид: x ’2 = –12 y ’ . Примечание. При вращении параболы вокруг ее оси образуется параболоид вращения Директриса параболы — такая прямая, кратчайшее расстояние от которой до любой точки, принадлежащей параболе, точно такое же, как расстояние от этой точки до фокуса. Вершина параболы — точка пересечения параболы с ее осью. Она считается началом системы координат, канонической для данной кривой. Вершина — середина перпендикуляра, опущенного из фокуса на директрису. Таким образом, директриса перпендикулярна оси симметрии и проходит на расстоянии р/2 от вершины параболы. Число р — фокальный параметр, расстояние от фокуса до директрисы. Поскольку все параболы подобны, именно эта характеристика определяет масштаб конкретной параболы. Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут. Каноническое уравнение параболы: Если расположить параболу слева от оси ординат, уравнение примет вид: Формула директрисы параболы имеет вид: Если вершину перенести в точку \((x_0;\;y_0)\) , отличную от начала осей координат, каноническое уравнение примет вид: Расстояние от точки фокуса (F) до любой точки параболы равняется расстоянию от этой точки к директрисе. Чтобы составить уравнение директрисы, нужно знать фокальный параметр. Фокальный параметр — половина длины хорды, проходящей через её фокус перпендикулярно фокальной оси. Задача №1 Составить уравнение директрисы параболы \(y^2\;=\;6x\) . Решение Сравнив каноническое уравнение с данным, получим: Уравнение директрисы — \(х\;=\;-\frac р2.\) В данном случае оно будет выглядеть так: Задача №2 Найти директрису параболы, заданной уравнением \(4х^2\;-\;12х\;+\;y\;+\;6\;=\;0.\) Решение Преображаем многочлен, находим полный квадрат относительно переменной х: Пусть \((y — 3)\) будет \(y_1\) , а \((х\;-\;\frac32)\) — \(х_1\) . Тогда, перенеся начало координат в точку \((x_1;\;y_1)\) , получим каноническое уравнение \(х_1^2\;=\;-y_1\) . Тогда уравнение директрисы — \(y_1=\;\frac1\) . Заменив \(y_1\) на \((y — 3)\) , получим уравнение: \(y\;–\;3\;=\;\frac1\)
$$
(\overrightarrow
$$
Но \(|\overrightarrow





Каноническое уравнение параболы
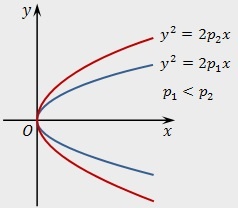
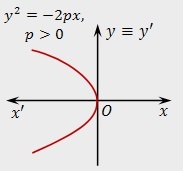
Уравнение директрисы параболы, если вершина не в пересечении осей координат
Алгоритм расчета
Фокус параболы
Примеры решения задач
Читайте также:

