Как сделать идеальный квадрат
Добавил пользователь Morpheus Обновлено: 04.10.2024
Идеальный (полный) квадрат - это такое натуральное число, квадратный корень которого будет являться целым числом.
Онлайн калькулятор определяет является ли число полным квадратом или нет.
Онлайн калькуляторы
Актуальная информация
Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день. Информация из официальных источников, постоянное обновление.
Идеальный совершенный магический квадрат
Идеальный магический квадрат – это матрица n x n , заполненная неповторяющимися числами таким образом, что, во-первых, сумма в каждой строке, каждом столбце, в каждой главной диагонали и в каждой ломаной диагонали равны магической константе, и, во-вторых, сумма любой пары центрально симметричных ячеек равна одному и тому же числу. Для матриц n x n , у которых n =2 k +1 и n =4 k , где k =2,3,4,… , удается скомпоновать идеальный магический квадрат, заполненный всеми числами от 1 до n 2 . При n =4 k +2, где k =1, 2, 3, …, идеальные квадраты существуют, но числа в них не являются частью начального натурального ряда. То есть данные идеальные магические квадраты могут быть только нетрадиционными. Пока еще не найдены идеальные магические квадраты 3 х 3 и 4 х 4 .
Идеальные магические квадраты проще всего строить при помощи латинских квадратов. Целью настоящей статьи является выявление наиболее простых и универсальных латинских квадратов, отталкиваясь от которого легко бы находились идеальные магические квадраты любого четного порядка.
1. Идеальные совершенные нетрадиционные магические квадраты
порядка n = 4 k + 2
От моего коллеги Н. Макаровой я узнал, что существует метод построения квадрата порядка 6, который описан в журнале "Наука и жизнь", № 5, 1978 г ., стр. 143. Сама Н.Макарова сумела развить этот метод и получила решения для 10х10, 14х14, 18х18, 30х30. Возможно, и для других n . Основная трудность состоит в нахождении первых двух полустолбцов. Например, для случая n = 14 она выявила такие полустолбцы ( см . Рис. 1):
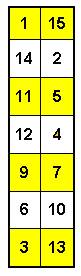
Рис. 1. Решение Н.Макаровой
Разными цветами выделены четные и нечетные числа.
Латинский квадрат в данном случае очень легко достраивается (Рис. 2):
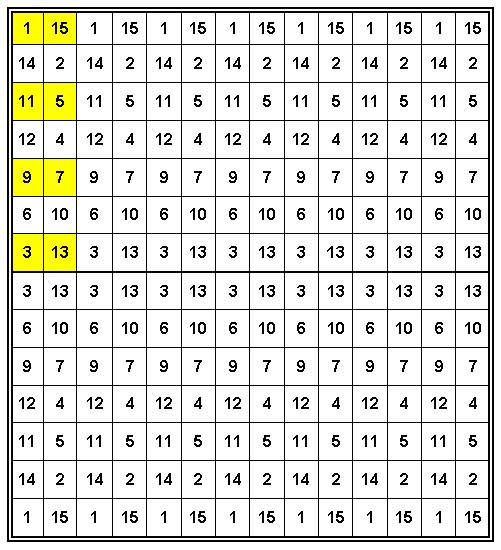
Рис. 2 . Латинский квадрат Н.Макаровой
Пусть числа в ячейках – это Z ( i , j ) , а Zmax – наибольшее число в поле латинского квадрата. Тогда идеальный нетрадиционный магический квадрат M ( i , j ) строится согласно правилу:
M( i,j ) = Zmax [Z( i , j ) – 1 ] + Z( j, i )
Допустим, начало координат находится в левом верхнем углу. Параметр i – номер строки , j – номер столбца. В нашем примере Zmax = 15. При i =2 j = 3 Z ( 2 , 3 ) = 14 ; Z ( 3 , 2) = 5. Следовательно, M ( 2 , 3 ) = 15 ( 14 – 1 ) + 5 = 200 . Вычислив таким образом все M ( i , j ), получим решение (Рис. 3):
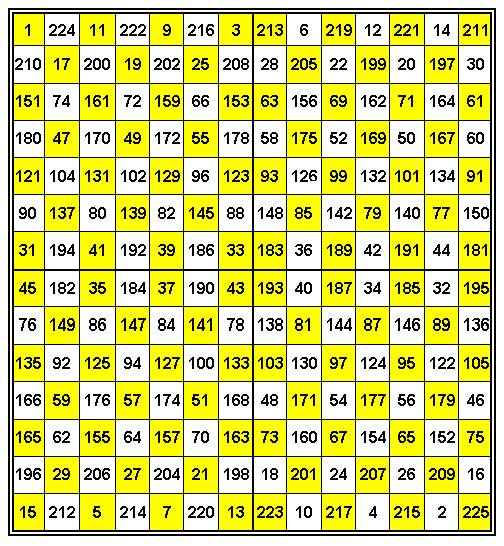
Рис. 3. Идеальный нетрадиционный совершенный магический квадрат Н.Макаровой.
Первое, на что я обратил внимание, - это отсутствие какой-либо явной закономерности в расстановке чисел на Рис.1. На числовые последовательности у меня особое чутье, ибо гляжу на них, как шахматист смотрит на расстановку фигур в процессе игры и просчитывает возможные ходы. Это происходит на уровне подсознания и в довольно быстром темпе. Попытаюсь подробно описать ходы моих рассуждений.
Глядя на рисунок 1, появляется ощущение дискомфорта, и возникают вопросы. Я мысленно говорю себе: ” Ну хорошо, пары четных и нечетных чисел регулярно чередуются. Но почему нечетные числа в левой колонке идут в последовательности 1 11 9 3 , а в правой – 15 5 7 13 ? Абсолютные разницы между соседними числами восхищения тоже не вызывают: 10 2 6 . У четных чисел тенденции не более логичные ( в левой колонке 14 12 6 , в правой - 2 4 10 ), при этом разницы: 2 и 6 . Получается, что прекрасный магический квадрат на Рис. 3 (идеальный и совершенный) вытекает из неясной последовательности четных и нечетных чисел. Это кажется мне странным”.
Далее формируются более конструктивные мысли: “На Рис. 3 показан четно-нечетный узор нетрадиционного идеального магического квадрата. Видно, что желтые ячейки с нечетными числами максимально распылены по всей матрице. Возникает подозрение: быть может, сильное распыление есть результат неудачного сочетания чисел в полустолбцах? Тогда можно попытаться кинуться в другую крайность – то есть получить узор в матрице, при котором четные и нечетные числа группировались бы в крупные блоки с соблюдением незыблемого правила: по всем 4 n направлениям (по строкам, столбцам, главным и ломаным диагоналям) количество желтых ячеек должно быть четным. В голове возникают две картинки, которые я года три-четыре назад досконально изучал при решении несколько иной задачи ( см . Рис. 4):
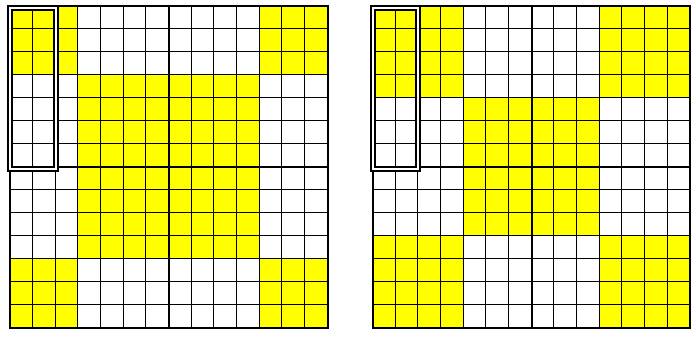
Рис. 4. Возможные схемы расположения четных и нечетных чисел.
Какая из этих схем более предпочтительна? Выделяю в каждой матрице два полустолбца.
Важно отметить, что тут нет никакой серьезной науки. На данные действия меня толкают ассоциации. Почему они такие – я сам толком не понимаю.
В первом случае сначала идут три пары нечетных чисел и затем четыре пары четных. Во втором – наоборот. Что же принять? “.
Когда при решении математической задачи оказывается избыток неизвестных параметров, обычно ищут дополнительные уравнения. Точно так же и я вынужден искать дополнительную цепочку логических выводов.
На помощь привлекаю следующую последовательность рассуждений: “Идеальных магических квадратов порядка 4 k +2 не существует. Это доказано математиками прошлого и позапрошлого веков. Можно построить только нетрадиционные идеальные квадраты, у которых максимальное число в ячейке определяется выражением ( n + m ) 2 , где m = 1, 3, 5, … . Параметр m довольно интересный: при одних его значениях нетрадиционные магические квадраты не строятся вообще, при других строятся, но с дублированием некоторых чисел. Для того , чтобы найти m , при котором нетрадиционный идеальный магический квадрат получался бы полноценным, приходится делать изнурительные комбинаторные расчеты. С увеличением порядка n усложняется и поиск приемлемого m .
Мне же желательно отыскать универсальный принцип задания этого параметра, чтобы без труда получалось решение для сколь угодно большой матрицы n x n . На этом этапе возникает потребность разрешить уже чисто философский вопрос: какое именно нечетное число m лучше всего характеризует порядок n = 4 k + 2 ? Постановка этого ключевого вопроса создает в голове вспышку озарения и обеспечивает ясное видение цели.
Конечно же: m = n /2 = 2 k + 1 ! !!
Итак, золотую рыбку я поймал. Теперь остается технически грамотно распорядиться ценной добычей.
Возвращаюсь к полустолбцам. На Рис. 5 показаны два возможных начала:
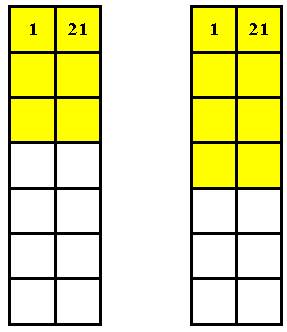
Число справа от единицы получаю элементарно: n + n /2 . При n = 14 это 21. Мне теперь известна постоянная S = 1,5 n + 1 = 22. Достаточно выявить по одному числу в каждой строке, чтобы найти его дополнение.
Теперь думаю: зачем под единицей помещать какое-то несоразмерно большое число? Раз нужно писать только нечетный ряд, то естественней всего задать его регулярным, то есть в виде арифметической прогрессии. Создаю предельно простые схемы (Рис. 6):
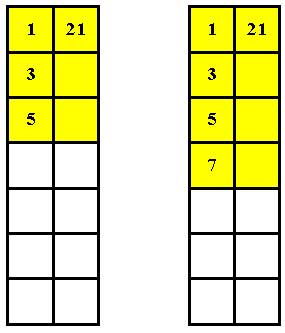
Только как быть с четными числами? Самое логичное было бы, чтобы весь левый ряд шел по нарастающей, то есть не имел бы “ дерганных точек”. Но с чего начать? Рассуждаю так: пусть в нижней левой ячейке будет стоять число, на единицу меньшее, чем 21 (Рис. 7):
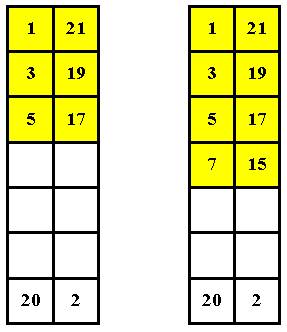
Логика тут простая – тогда правый полустолбец снизу-вверх будет заполняться последовательным рядом четных чисел, начиная с 2-х. Сохраняю ранее принятую тенденцию и окончательно записываю (Рис. 8):
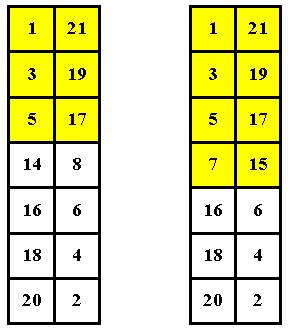
Замечаю, что в варианте на Рис. 8 a ) после последнего нечетного числа 5 идет первое четное число 14.
Но ведь это как раз порядок матрицы n ! !!
Я уже почти уверен, что именно два левых полустолбца приведут к успеху”.
Быстро составляю программу на языке Yabasic :
rem ПОСТРОЕНИЕ НЕТРАДИЦИОННОГО ИДЕАЛЬНОГО МК ПОРЯДКА 4 k +2
dim z1( nn,nn ),z2(nn,nn2),z( nn,nn ),a(nn/2),c(900000)
n=530 :k =n/2:k1=(n-2)/4:x=(n+k+1)/2:n1= n+k:s =n1+1:m=n/2*(n1^2+1)
for i =1 to k1:a( i )=2*i-1:next i:for i =1 to k1+1:a(n/2-i+1)=n1-1-2*(i-1):next i:for i =1 to n/2:z1(i,1)=a( i ):next i
for i =n/2+1 to n:z1(i,1)=z1(n-i+1,1):next i
for i =1 to n:z1(i,2)=s-z1(i,1):next i:for k0=1 to n/2-1
for i =1 to n:z1(i,2*k0+1)=z1(i,1):z1(i,2*k0+2)=z1(i,2):next i
next k0:u=0:for i =1 to n:for j=1 to n:z ( i,j )=n1*(z1( i,j )-1)+z1( j,i ):next j:next i:s0=0:for i =1 to n:s0=0:for j=1 to n:s0=s0+z( i,j ):next j:if s0=m then u=u+1:fi:next i:s0=0:for j=1 to n:s0=0:for i =1 to n:s0=s0+z( i,j ):next i:if s0=m then u=u+1:fi:next j:for i =1 to n:for j=n+1 to n+n:z ( i,j )=z( i,j -n):next j:next i:s0=0:for j=1 to n:s0=0:for i =1 to n:s0=s0+z(i,i+j-1):next i:if s0=m then u=u+1:fi:next j:s0=0:for j=1 to n:s0=0:for i =n to 1 step -1:s0=s0+z(i,i+j-1):next i:if s0=m then u=u+1:fi:next j
Здесь производится проверка на пандиагональность и на отсутствие дублирования чисел. Мои ожидания полностью оправдались: по единому принципу находятся все идеальные нетрадиционные магические квадраты порядка 4 k + 2. Общая схема составления двух полустолбцов следующая (Рис. 9):
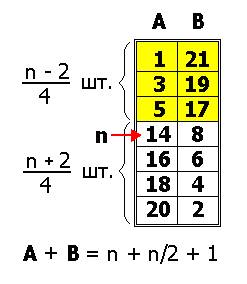
Рис. 9 . Универсальный способ построения двух полустолбцов,
Даже и не знаю – можно ли изобрести более простую цепь чисел?
Характерные точки: 5 ----> ( n – 4)/2 ; 20 ----> 1,5 n – 1 ; 17 ----> n + 3 ; 8 ----> ( n + 2)/2 .
Латинский квадрат в этом случае такой (Рис. 10):
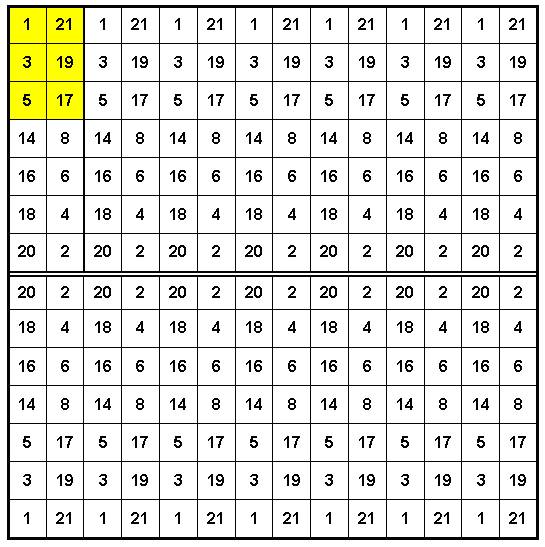
Рис. 10. Латинский квадрат Г.Александрова при n = 14
Окончательное решение для n = 14 (Рис. 11):
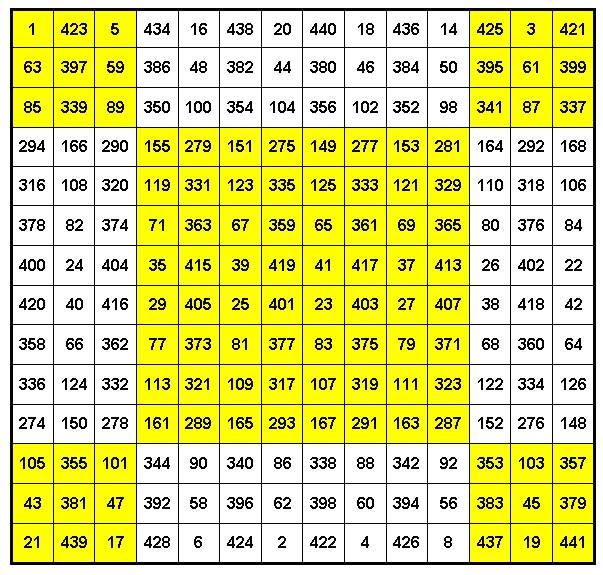
Рис. 11. Идеальный нетрадиционный совершенный магический квадрат Г.Александрова 14 х 14
Следует заметить, что пары чисел в строках (Рис. 9 ) можно как угодно менять местами. В результате все равно будут получаться идеальные нетрадиционные магические квадраты.
2. Идеальные совершенные магические квадраты
порядка 8 k и 8 k + 4
Описанный выше метод построения латинских квадратов можно использовать и для всех остальных четных порядков n , то есть для n = 8 k и n = 8 k + 4. Различия – только в наборе чисел в двух полустолбцах. Здесь параметр m = 0 и, следовательно, магические квадраты являются традиционными.
Вот как мне удалось решить эту задачу.
Поскольку m =0, то в двух полустолбцах должны быть задействованы все числа от 1 до n . Так как n – число четное, то обязательно присутствуют n /2 нечетных чисел и столько же четных. Создадим пробные регулярные схемы, например, такие (Рис. 12):
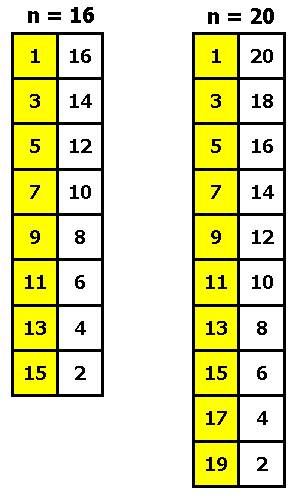
Рис. 12. Регулярное заполнение числами полустолбцов
У меня была слабая надежда, что решение сразу получится. Однако , чудес в сложных задачах не бывает. Тогда пришла в голову мысль: буду менять местами нечетные и соответствующие им четные дополнения. Использовал для этой цели метод Монте-Карло. То есть случайным образом задавал как количество пар чисел, которые нужно обменять, так и места их расположения (т.е. номера строк). К счастью, на мониторе стали появляться долгожданные цепочки чисел, характеризующие идеальные совершенные магические квадраты. Просмотрев все варианты и проанализировав их для разных значений n , мне удалось найти две общие схемы построения полустолбцов (Рис. 13):
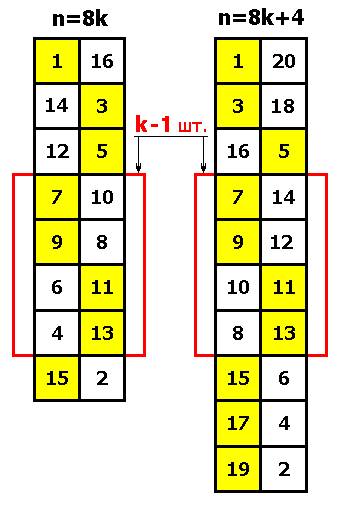
Рис. 13 Универсальные способы построения двух полустолбцов,
Блок в красной рамке повторяется k - 1 раз один за другим. Видно, что регулярность четных и нечетных чисел сохранилась – просто они стали располагаться не строго вертикально, а “змейками“. Эти две модели справедливы для любого k , начиная с единицы. Опять же, пары чисел потом можно как угодно менять в полустолбце – все равно получится идеальный совершенный магический квадрат.
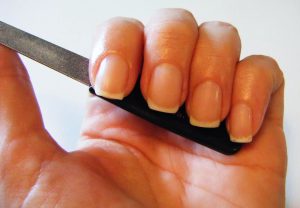

Как сделать квадратную форму ногтей: техника исполнения и основные приемы

По мере роста ногтевой пластины придется освоить технологию того, как из круглой формы ногтей сделать квадратную. Для начала нужно будет максимально до верхнего края ногтевого ложе спилить все ноготки по прямой линии. Образовавшиеся в углах неровности, дабы ногти не смотрелись странно, следует немного скруглить. Затем, по мере отрастания ногтей, опять потребуется корректировка кончиков ногтей по прямой линии. Так постепенно ногти приблизятся к размеру, когда можно будет сделать мягкий квадрат – с небольшими закруглениями в уголках. И уже только тогда, когда прямая линии кончика ногтя будет проходить от края к краю, образуя у свободного края четкие прямые углы, можно говорить о квадратной форме.

Выше обозначенная техника характерна для вопроса того, как сделать квадратные ногти из круглых. Если же длина достаточная, то остается только найти способ того, как правильно подпилить ногти квадратом. Как это сделать мы постараемся объяснить максимально доступным образом и закрепить визуально.
Как правильно пилить квадратные ногти? Все очень просто. Действовать придется в трех направлениях – подпилить кончики ногтей до ровного прямого среза, а затем задать направление боковым граням ногтей, опять-таки строго по прямой линии. В результате по краям свободного кончика должны образоваться два прямых угла.
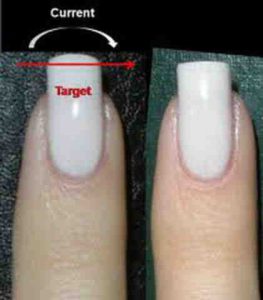
Довольно часто у новичков проблема заключается именно в создании этих самых пресловутых прямых углов. Зачастую один из уголков оказывается выше, острее или, напротив, более широкий. Чтобы этого не произошло, воспользуйтесь маленькой хитростью, которую используются даже профессионалы, помогающей им как правильно пилить ногти квадратной формы, так и придать красивые очертания пластинам. В процессе формирования ногтя подставляете пилочку к основанию ногтевого ложе и следите за тем, что кончик ногтя был ее параллелен. Естественно, что для этих целей понадобится пилочка прямой формы. Что касается углов, то здесь, уже после того, как будет придана форма кончику, необходимо подпиливать ноготь четко под прямым углом.
И еще одно важно правило, как подпиливать ногти квадратной формы – совершаете движения пилочкой строго в одном направлении. Это позволит вам избежать ломкости и расслоения ногтей. Впрочем, данное правило актуально для придания любой формы.
Смотрите, изучайте, а потом применяйте на практике. Быть может, со временем, и вы создадите собственную, отличную от остальных, технику создания красивых ногтей, а пока видеоурок о том, как правильно подпиливать ногти квадратной формы.
Как сделать квадратные ногти красивыми?


Необязательно останавливаться на нюдовых оттенках. В качестве основы можно выбрать пастель или даже яркий цвет (розовый, голубой, сиреневый и т.п.), Важно соблюдать только одно правило в основе всегда должен быть лак более светлого оттенка, в центре – темный. Именно такой способ окрашивания позволяет создать иллюзию боле тонких и вытянутых пластин.


Визуально удлинить короткие пластины поможет и классический френч, но здесь важно разместить линию улыбки чуть выше ее естественной границы. Однако если пластины не только короткие, но и широкие, то белая улыбка на квадратной форме еще сильнее обозначит непривлекательные размеры пластины. Если у вас именно такая проблема, присмотритесь к нестандартному варианту френча – прорисовывайте улыбку темным лаком. Такой прием поможет визуально сузить пластины.


Для широких пластин омбре следует выполнять в вертикальной технике – обозначив центр светлым пигментом, а края окрасив в более темные оттенки.

Также короткие и широкие пластины спасет дизайн с вертикальными линиями. Они зрительно добавят недостающей длины и сузят ногти. А вот горизонтальные линии под запретом.

Фото с сайта: krasotka.cc


Чтобы вырезать ровный квадрат из прямоугольного листа бумаги, вы можете воспользоваться одним из следующих способов.
Способ №1
- Разложите лист бумаги на столе
- Загните верхний левый угол по диагонали
- Проведите прямую линию от основания диагонального сгиба до противоположного края листа
- Разверните лист в исходное положение и разрежьте его по проведенной линии - у вас получится квадрат и узкий прямоугольник.

Способ №2
Если у вас под рукой нет карандаша, сделайте следующее:
- Возьмите 2 прямоугольных листа бумаги
- Поверните один из листов на 90 градусов и подложите его под другой так, чтобы их края в точности совпадали с левой стороны
- Используя правую кромку верхнего листа в качестве направляющего ориентира, отрежьте выглядывающую из-под него часть нижнего листа
- Уберите верхний лист
Как и в первом случае, нижний лист будет разделен на квадрат и узкий прямоугольник.
Читайте также:

