Как сделать эскиз графика функции

Добавил пользователь Владимир З.
Обновлено: 05.10.2024

Для многих учащихся, тема "Графики" и все что с ними связано, очень сложна и почти все как один говорит, что не понимает их. А на самом деле, все легко. Достаточно уметь выполнять простые арифметические действия. Если сравнивать задания из второй части ОГЭ по математике, то решить текстовую задачу, чаще бывает сложнее, чем построить график и ответить на вопрос. Сложность заключается в том, что задача требует размышления, правильного прочтения текста, и составление математической модели. При выполнения заданий на построение графиков, нужно всего лишь следовать алгоритму построения. Что можно описать конкретными шагами, то всегда легко.

Разберем построение следующего графика функции и определим шаги для выполнения таких заданий.

С помощью программы Desmos можно построить график одной или нескольких функций. Каждая новая функция вводится с новой строки. Для добавления точек с координатами (x,y) используйте + и вид table . Для добавления одной точки достаточно указать, например, A=(3.5,6.1) .
Чтобы настроить вид координатной сетки (пределы по осям и стрелки) используйте .

Для задания области (например, 1≤x≤7 ) используйте пределы или >= .

Трехмерные графики функции

Построить графики (в том числе и трехмерные) можно также, используя следующий сервис. Например, построить график функции cosx + e sinx+x 3 . Записываем как cos(x)+exp((sin(x)+x^3)) и нажимаем кнопку Построить график .
Чтобы построит два графика в одних координатах, например, y=3x-1, y=x 2 -2x+5 , указываем: 3*x-1,x^2-2*x+5 . Также можно задать пределы отображения по оси X (ось абсцисс).

Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3 ).

Также можно начертить график по точкам. Необходимо вставить данные для X (первый столбец) и Y (второй и последующие столбцы).

На первом этапе при заданном интервале [a;b] и шаге h рассчитываются значения функции y=f(x) .
На втором этапе с помощью инструмента Excel Мастер диаграмм строится визуализация рассчитанных значений.

Чтобы построить трехмерный график в Excel , необходимо указать функцию f(x,y) , пределы по x и y и шаг сетки h .

Принципы и способы построения графика функции

При прямом вычислении значений функции y=f(x) необходимо задать интервал [a;b] вычислений и шаг h . Получается таблица, по которой можно построить график.
Например, определим для функции y=x*e 2x /3+4 интервал [-3;7], на котором будем отображать найденные точки. Чем меньше шаг h , тем точнее график функции (другими словами, тем точнее аппроксимация). Например, при h=2 количество точек для построения равно N=(7-(-3))/2+1=6 (-3; -1; 1; 3; 5; 7), а при h=0.1 уже N=(7-(-3))/0.1+1=101 .
Построение графика функции методом дифференциального исчисления предполагает схематичное построение, используя свойства функции.

Прикладное применение графика функции

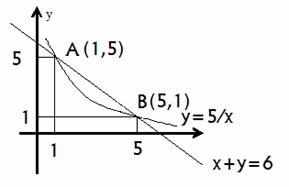
. . . . к графику функции. к графику функции: . . . при определении точек разрыва: . :

1. Найти область определения функции, классифицировать точки разрыва
2. Исследовать функцию на четность и периодичность
3. Провести анализ асимптотического поведения функции (наличие вертикальных, горизонтальных и наклонных асимптот) (см. §41 данного справочника)
4. Взять первую производную. Определить критические точки, интервалы монотонности, точки экстремума
5. Взять вторую производную. Определить критические точки 2-го порядка, интервалы выпуклости и точки перегиба
6. Найти точки пересечения функции с осями координат (если уравнение $f(x)=0$ не имеет аналитического решения, указать количество точек пересечения с осью OX)
7. Построить график функции

п.2. Примеры

4) Первая производная \begin f'(x)=2\cdot 3x^2-6\cdot 2x-18\cdot 1+0=6x^2-12x-18=6(x^2-2x-3)=\\ =6(x-3)(x+1)\\ f'(x)=0\ \text\ \left[ \begin x=3\\ x=-1 \end \right. \end Критические точки: $x=-1$ и $x=3$
Составляем таблицу:

$x$	$(-\infty;-1)$	-1	(-1;3)	3	$(3;+\infty)$
$f'(x)$	>0	0	0
$f(x)$	$\nearrow$	max	$\searrow$	min	$\nearrow$

5) Вторая производная: \begin f''(x)=(6x^2-12x-18)'=6\cdot 2x-12\cdot 1-0=12x-12=12(x-1)\\ f''(x)=0\ \text\ x=1 \end Критическая точка 2-го порядка: $x=1$
Составляем таблицу:

Пример 2. Постройте график функции $y=\frac3x+\frac x3$
1) Область определения
ОДЗ: $x\ne 0$
$x=0$ - точка разрыва. Исследуем односторонние пределы: \begin \lim_\left(\frac 3x+\frac x3\right)=\frac+0=-\infty,\ \ \lim_\left(\frac 3x+\frac x3\right)=\frac+0=+\infty \end Пределы не равны и бесконечны. $x=0$ - точка разрыва 2-го рода.

2) Четность $$ f(-x)=\frac+\frac=-\left(\frac 3x+\frac x3\right)=-f(x) $$ Функция нечётная.
Периодов нет. Функция не периодическая.

3) Асимптоты
1. Вертикальная асимптота $x=0$ – точка разрыва 2-го рода
2. Горизонтальные асимптоты \begin b_1=\lim_\left(\frac 3x+\frac x3\right)=0+(-\infty)=-\infty\\ b_2=\lim_\left(\frac 3x+\frac x3\right)=0+(+\infty)=+\infty \end Пределы бесконечны, горизонтальных асимптот нет.
3. Наклонные асимптоты: \begin k_1=\frac1x \lim_\left(\frac 3x+\frac x3\right)=\lim_\left(+\frac13\right)=0+\frac13=\frac13\\ k_1=\frac1x \lim_\left(\frac 3x+\frac x3\right)=\lim_\left(+\frac13\right)=0+\frac13=\frac13\\ k=k_1=k_2=\frac13 \end Ищем b: $$ b=\lim_(y-kx)=\lim_\left(\frac3x+\frac x3-\frac x3\right)=\lim_\frac 3x=0 $$ Есть одна наклонная асимптота $y=\frac 3x$
Кривая стремится к ней на минус и плюс бесконечности.

$x$	$(-\infty;-3)$	-3	(-3;0)	0	$(0;3)$	3	$(3+\infty)$
$f'(x)$	>0	0	0
$f(x)$	$\nearrow$	max	$\searrow$	$\varnothing$	$\searrow$	min	$\nearrow$

Функция возрастает при $x\in(-\infty;-3)\cup(-3;+\infty)$
Функция убывает при $x\in(-3;0)\cup(0;3)$
Точка максимума $x=-3;\ y_=f(-3)=-1-1=-2$
Точка минимума $x=3;\ y_=f(3)=1+1=2$

5) Вторая производная: \begin f''(x)=\frac13\left(1-\frac\right)'=\frac13\left(0+\frac\right)=\frac \end Вторая производная нулей не имеет.
Критическая точка 2-го порядка: $x=0$
Составляем таблицу:

Функция выпуклая вверх при $x\in(-\infty;0)$
Функция выпуклая вниз при $x\in(0;+\infty)$
Точек перегиба нет.

6) Точки пересечения с осями
Пересечение с осью OY: $x=0\notin D$ - не входит в ОДЗ, пересечений с OY нет
Пересечение с осью OX:
$\frac3x+\frac x3=0\Rightarrow \frac=0\Rightarrow x\in \varnothing$ - решений нет, пересечений с OX нет

7) График

Пример 3*. Постройте график функции $y=\frac$
Сколько корней имеет уравнение $\frac=a$?

1) Область определения
ОДЗ: $x\ne 1$
$x=1$ - точка разрыва. Исследуем односторонние пределы: \begin \lim_\frac=\frac=\frac=+\infty\\ \lim_\frac=\frac=\frac=-\infty \end Пределы не равны и бесконечны. $x=1$ - точка разрыва 2-го рода.

2) Четность $$ f(-x)=\frac\ne \left[ \begin f(x)\\ -f(x) \end \right. $$ Функция ни четная, ни нечетная.
Периодичность: функция не периодическая

$x$	$(-\infty;-2)$	-2	(-2;1)	1	$(1;2)$	2	$(2+\infty)$
$f'(x)$	0	$\varnothing$	>0	0	0	$\varnothing$	0
$f(x)$	$\cap$	перегиб	$\cup$	$\varnothing$	$\cap$	перегиб	$\cup$

Функция выпуклая вверх при $x\in(-\infty;x_1)\cup(1;x_2)$
Функция выпуклая вниз при $x\in(x_1;1)\cup (x_2;++\infty)$
Точки перегиба: $$ \begin x=\frac>\approx -3,37\\ y\approx 0,51 \end,\ \ \begin x=\frac>\approx 2,37\\ y\approx 3,62 \end $$
6) Точки пересечения с осями
Пересечение с OY: $x=0,\ y=\frac=4$
Пересечение с осью OX:
$\frac=0\Rightarrow x=\sqrt[3],\ y=0$

7) График

Чтобы узнать количество корней уравнения $\frac=a$, нужно снизу вверх двигать горизонталь $y=a$ и считать количество точек её пересечения с графиком функции.
Последовательно, получаем:
$a\lt\frac$ - один корень
$a=\frac49$ – два корня
$\frac49\lt a\lt 1$ - три корня
$a=1$ – два корня
$1\lt a\lt 4$ – три корня
$a=4$ - два корня
$a\gt 4$ - один корень

Ответ:
$a\lt\frac49\cup a\gt 4$, один корень
$a=\left\$, два корня
$\frac\lt 1\lt 1\cup 1\lt a\lt 4$, три корня

Пример 4*. Постройте график функции $y=sin^4⁡x+cos^4⁡x$, используя правила преобразования тригонометрических функций и с помощью стандартной процедуры исследования функции

1) Область определения $x\in\mathbb$

2) Четность $$ f(-x)=sin^4(-x)+cos^4(-x)=sin^4x+cos^4x=f(x) $$ Функция четная.

Чтобы найти период, преобразуем тригонометрическое выражение, применяя формулы понижения степени (см. §15 данного справочника): \begin sin^4x+cos^4x=\left(\frac\right)^2+\left(\frac\right)^2=\\ =\frac14(1-2cos2x+cos^2 2x+1+2cos2x+cos^2 2x)=\frac=\\ =\frac12\left(1+\frac\right)=\frac \end Функция периодическая с периодом $T=\frac<2\pi>=\frac \pi 2$
Исходя из полученного выражения и применяя правила преобразования графиков тригонометрических функций (см. §8 данного справочника), можно сразу получить результат. $$ y=\frac=\frac34+\frac14 cos4x $$ Цепочка преобразований: $$ x \xrightarrow1 4x\xrightarrow2 cos4x \xrightarrow3 \frac14\xrightarrow4 \frac34+\frac14 cos4x $$ Пошагово получаем:
1. Умножение аргумента на 4 приводит к уменьшению периода в 4 раза $T=\frac\pi 2$
2. Косинус – функция четная, при $x=0,\ cos⁡4x=1$, остальные единицы будут через период: $x=\frac<\pi k>,\ cos⁡4x=1$. Соответственно: $x=\frac\pi 4+\frac<\pi k>0\ ,cos⁡4x=-1$.
Нули функции: $x=\frac\pi 8+\frac<\pi k>,\ cos⁡4x=0$.
3. Умножение на $\frac14$ уменьшает амплитуду косинусоиды в 4 раза: $-\frac14\leq\frac14 cos4x\leq \frac14$
4. Прибавление $\frac34$ перемещает график на $\frac34$ вверх: $\frac12\leq\frac34+\frac14 cos4x\leq 1$

Получаем график:

Продолжим стандартное исследование функции.

3) Асимптоты
1. Вертикальных асимптот нет, т.к. нет точек разрыва 2-го рода.
2. Горизонтальных асимптот нет, т.к. нет пределов на бесконечности.
3. Наклонных асимптот нет, т.к. на бесконечности отношение ограниченной тригонометрической функции к бесконечному x дает $k=0$.

4) Первая производная:
Исследуем промежуток, равный одному периоду $T=\frac\pi 2,\ 0\leq x\leq\frac\pi 2$ \begin f'(x)=(sin^4 x+cos^4 x)'=\left(\frac\right)'=0-\frac14\cdot 4\cdot sin4x=-sin4x\\ sin4x=0\Rightarrow 4x=\pi k\Rightarrow x=\frac<\pi k> \end Критические точки: $x=\frac<\pi k>$. На периоде $T=\frac\pi 2$ получаем три точки $x=\left\<0;\frac\pi 4;\frac\pi 2\right\>$

$x$	0	$\left(0;\frac\pi 4\right)$	$\frac\pi 4$	$\left(\frac\pi 4;\frac\pi 2\right)$	$\frac\pi 2$
$f'(x)$	0	0	0
$f(x)$	1 max	$\searrow$	$\frac12$ min	$\nearrow$	1 max

Функция убывает при $x\in\left(\frac<\pi k>;\frac\pi 4+\frac<\pi k>\right)$
Функция возрастает при $x\in\left(\frac\pi 4+\frac<\pi k>;\frac\pi 2+\frac<\pi k>\right)$
Точки минимума $x=\frac\pi 4+\frac<\pi k>;\ y_=\frac12$
Точки максимума $x=\frac<\pi k>;\ y_=1$

5) Вторая производная: \begin f''(x)=(-sin4x)'=-4cos4x\\ cos4x=0\Rightarrow 4x=\frac\pi 2+\pi k\Rightarrow x=\frac\pi 8+\frac<\pi k> \end Критические точки 2-го порядка: $x=\frac\pi 8+\frac<\pi k>$.
На периоде $T=\frac\pi 2$ получаем две точки $x=\left\<\frac\pi 8;\frac<3\pi>\right\>$

Утверждено научно-методическим советом факультета прикладной математики, информатики и механики 25 мая 2011 г., протокол № 10.

Рецензент д-р физ. мат. наук, профессор А. Д. Баев

Учебно-методическое пособие по дисциплине "Математический анализ" подготовлено на кафедре математического и прикладного анализа факультета прикладной математики, информатики и механики Воронежского государственного университета

Рекомендуется для студентов первого курса очной и очно-заочной форм обучения

Для направлений 010400.62 "Прикладная математика и информатика", 010300.62 "Фундаментальная информатика и информационные технологии", 010500 "Математическое обеспечение и администрирование информационных систем", 080500.62 "Бизнес-информатика", 010800.62 "Механика и математическое моделирование".

Оглавление

Часть 1. Построение эскизов графиков функций. 4

1. Графики основных элементарных функций……………………………………. 4

1.1. Постоянная и степенная функции. 5

1.2. Показательная и логарифическая функции. 8

1.3. Тригонометрические функции. 9

1.4. Обратные тригонометрические функции. 11

2. Элементарные преобразования графиков……………………………………… 12

3. Построение графиков функций, не являющихся элементарными……………. 16

4. Действия с графиками функций………………………………………………… 19

4.1. Сложение и вычитание графиков. 19

4.2. Умножение и деление графиков. 22

4.3. Построение графиков сложных функций. 28

5. Графики в полярных координатах……………………………………………… 32

5.1. Полярные координаты.. 32

5.2. Графики кривых в полярных координатах. 33

Часть 2. Применение дифференциального исчисления к исследованию функций и построению их графиков. 38

1. Признак возрастания и убывания функции…………………………………….. 38

2. Локальные экстремумы функции……………………………………………….. 39

3. Выпуклость функции. Точки перегиба…………………………………………. 43

5. Порядок построения графика функции, заданной выражением …….. 49

6. Построение графика функции, заданной параметрически……………………. 53

6.1. Порядок построения графика параметрически заданной функции. 53

6. 2. Асимптоты параметрического графика. 54

6. 3. Точки перегиба. 54

6.4. Пример построения графика параметрически заданной функции. 55

Список литературы.. 58

Введение

Методическое пособие составлено из двух частей: в первой части рассматривается построение эскизов графиков функций, во второй - построение графиков функций с использованием техники дифференцирования. Для построения эскизов графиков функций применяются следующие приемы: построение "по точкам", действия с графиками (например, сложение, вычитание, умножение графиков), преобразование графиков.

Часть 1. Построение эскизов графиков функций

В этой части мы будем изучать построение графиков функций, используя наименьшее число вычисление и избегая прямого применения дифференциального исчисления. Такие эскизы иллюстрируют общее поведение функции и полезны при решении различных задач.

В первом разделе этой части мы построим графики основных элементарных функций в прямоугольной декартовой системе координат и отметим некоторые особенности поведения этих функций.

Во втором разделе изучим элементарные преобразования графиков функций, таких как параллельный перенос, поворот, зеркальное отображение, растяжение, сжатие и др.

В третьем разделе построим графики некоторых функций, не являющихся элементарными.

В четвертом разделе разберем как производить сложение, вычитание, умножение и деление графиков, а также как строить график сложной функции.

В пятом разделе мы рассмотрим полярную систему координат и построим в ней графики некоторых функций, наиболее часто встречающихся в приложениях.

Тригонометрические функции

Тригонометрические функции и опредены на всей числовой оси, переодические, с периодом и не принимают значения по абсолютной величине большие . Отметим также, что функция является нечетной, а функция - четной. Их графики изображены на рис. 7.

Линия, являющаяся графиком функции , называется синусоидой. График функции - тоже синусоида, она получается из графика смещением вдоль влево на отрезок .

Из рис. 7 видно, что график функции проходит через точку - начало координат, а функция проходит через точку . Графики обеих функций и и пересекают ось неограниченное число раз, это означает, что уравнения и имеют бесконечно много корней. Именно, решение уравнения имеет вид , где - целое число, а решением уравнения будут число , где - целое число.

Рис. 7. Графики функции и .

Тангенс и котангенс выражаются формулами и , а в такой форме записи видно, что графики этих функций будут иметь бесконечно много точек разрыва. Действительно, у в знаменателе находится , который обращается в нуль в точках , а будет иметь разрывы там, где синус равен нулю, т.е. в точках ( - целое число).

Обе функции и и являются нечетными и периодическими с периодом . Графики этих функций приведены на рис. 8.

Рис. 8. Графики функции и .

Список литературы

1. Данко П. Е. Высшая математика в упражнениях и задачах в двух частях, часть I, издание четвертое, исправленное и дополненное // П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - М: "Высшая школа", 1986.

2. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления // Г.М. Фихтенгольц. T.1. - СПб: Лань, 1997.

3. Смирнов В. И. Курс высшей математики // В. И. Смирнов. Т.1. - М: Наука, Гл. ред. физ.-мат. лит., 1974.

4. Савелов А. А. Замечательные кривые // А. А. Савелов. - Томск: Красное знамя, 1938.

5. Савелов А. А. Плоские кривые // А. А. Савелов. - М: ГИФМЛ, 1960.

6. Виноградова И. А. Задачи и упражнения по математическому анализу. В 2-х кн. Кн. 1. Дифференциальное и интегральное исчисление функций одной переменной: Учеб. пособие.– 2-е изд., перераб. / И. А. Виноградова, С. Н. Олехник, В. А. Садовничий. Под ред. В. А. Садовничего. – М: Высш. шк., 2000.

7. Каплан И. А. Практические занятия по высшей математике // И. А. Каплан. - Харьков: изд-во Харьковского ордена трудового красного знамени гос. ун-та им. А. М. Горького, 1967.

8. Харди Г. Х. Курс чистой математики // Г. Х. Харди. - М: гос. изд-во иностр. лит., 1949.

ГРАФИКИ ФУНКЦИЙ

Учебно-методическое пообие для вузов

Воронежского государственного университета

Рецензент д-р физ. мат. наук, профессор А. Д. Баев

Рекомендуется для студентов первого курса очной и очно-заочной форм обучения

Оглавление

Часть 1. Построение эскизов графиков функций. 4

1. Графики основных элементарных функций……………………………………. 4

1.1. Постоянная и степенная функции. 5

1.2. Показательная и логарифическая функции. 8

1.3. Тригонометрические функции. 9

1.4. Обратные тригонометрические функции. 11

2. Элементарные преобразования графиков……………………………………… 12

3. Построение графиков функций, не являющихся элементарными……………. 16

4. Действия с графиками функций………………………………………………… 19

4.1. Сложение и вычитание графиков. 19

4.2. Умножение и деление графиков. 22

4.3. Построение графиков сложных функций. 28

5. Графики в полярных координатах……………………………………………… 32

5.1. Полярные координаты.. 32

5.2. Графики кривых в полярных координатах. 33

Часть 2. Применение дифференциального исчисления к исследованию функций и построению их графиков. 38

1. Признак возрастания и убывания функции…………………………………….. 38

2. Локальные экстремумы функции……………………………………………….. 39

3. Выпуклость функции. Точки перегиба…………………………………………. 43

5. Порядок построения графика функции, заданной выражением …….. 49

6. Построение графика функции, заданной параметрически……………………. 53

6.1. Порядок построения графика параметрически заданной функции. 53

6. 2. Асимптоты параметрического графика. 54

6. 3. Точки перегиба. 54

6.4. Пример построения графика параметрически заданной функции. 55

Список литературы.. 58

Введение

Часть 1. Построение эскизов графиков функций

В третьем разделе построим графики некоторых функций, не являющихся элементарными.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х, а на оси ординат - значения функции у = f (х).

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x).

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х.

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x), то для нахождения числа f(а) (т. е. значения функции в точке х = а) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х 2, отрицательные - при 0 2 - 2х принимает при х = 1.

Для построения графика функции f(x) нужно найти все точки плоскости, координаты х, у которых удовлетворяют уравнению y = f(x). В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно - с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений - скажем, х₁, х₂, x₃ . х_k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x). Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.

Пример 1. Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x)|, где f(х) - заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х), у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x), имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x), которая лежит ниже оси х, следует симметрично отразить относительно оси х).

Пример 2. Построить график функции у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х 2 - 2x|.

Сначала построим график функции y = x 2 - 2x. График этой функции - парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 —2х|, исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x).

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f

Пусть точки (х₀, y₁) и (х₀, у₂) соответственно принадлежат графикам функций y = f 1 = f(x₀), y₂ = g(х₀). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х₀) + g(x₀) = y1 +y2),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x). и y = g(х) заменой каждой точки (х_n, у₁) графика функции y = f(x) точкой (х_n, y₁ + y₂), где у₂ = g(x_n), т. е. сдвигом каждой точки (х_n, у₁) графика функции y = f(x) вдоль оси у на величину y₁ = g(х_n). При этом рассматриваются только такие точки х_n для которых определены обе функции y = f(x) и y = g(x).

Такой метод построения графика функции y = f(x) + g(х) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4. На рисунке методом сложения графиков построен график функции
y = x + sinx.

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

Читайте также:

\(x\)	\((-\infty;-1)\)	-1	(-1;3)	3	\((3;+\infty)\)
\(f'(x)\)	>0	0	0
\(f(x)\)	\(\nearrow\)	max	\(\searrow\)	min	\(\nearrow\)

\(x\)	\((-\infty;-3)\)	-3	(-3;0)	0	\((0;3)\)	3	\((3+\infty)\)
\(f'(x)\)	>0	0	0
\(f(x)\)	\(\nearrow\)	max	\(\searrow\)	\(\varnothing\)	\(\searrow\)	min	\(\nearrow\)

\(x\)	\((-\infty;-2)\)	-2	(-2;1)	1	\((1;2)\)	2	\((2+\infty)\)
\(f'(x)\)	0	\(\varnothing\)	>0	0	0	\(\varnothing\)	0
\(f(x)\)	\(\cap\)	перегиб	\(\cup\)	\(\varnothing\)	\(\cap\)	перегиб	\(\cup\)

\(x\)	0	\(\left(0;\frac\pi 4\right)\)	\(\frac\pi 4\)	\(\left(\frac\pi 4;\frac\pi 2\right)\)	\(\frac\pi 2\)
\(f'(x)\)	0	0	0
\(f(x)\)	1 max	\(\searrow\)	\(\frac12\) min	\(\nearrow\)	1 max