Как сделать значение функции

Обновлено: 07.07.2024

Что значить задать функцию? Какими способами можно задать функцию? Что такое определение функции?

Задать функцию — это значит указать правило, при задании любого значения аргумента x вы найдете значение функции y.

Функция y=f(x) – зависимость переменной y от переменной x. Когда задаем значение аргумента x, получаем единственное значение функции y.

Способы задания функции.

В данной статье рассмотрим 3 способа задания функции. На самом деле их больше, в школьной программе чаще всего разбирают эти способы задания функции.

Аналитический способ задания функции.

Чаще всего в школьной программе правило задают в виде формулы y=f(x), x∈X или нескольких формул. Такой способ задания функции называется аналитическим.

Примеры аналитического задания функции:

Графический способ задания функции.

Также если по формуле построить график функции, то данный способ задания функции будет называться графическим. Не всегда вам будут давать график совместно с формулой. Иногда вам в заданиях будут давать только график функции, по которому вы должны будете найти определенные данные. По графику функции можно восстановить его формулу, но это не всегда легко сделать, все зависит от начерченного графика. В школьной программе вам будут задавать графики, по которым вы сможете рассчитать формулу.

Примеры, графического задания функции:

Табличный способ задания функции.

Следующий способ задания функции применяется чаще всего на практике называется табличный.

Все данные представлены в виде таблице. У этого способа имеется конечное множество значений аргумента. Такими таблицами вы уже пользовались в алгебре, например, таблица квадратов, таблица корней и т.д.

Примеры, табличного задания функции:

x	1	2	3	4	5	6	7	8	9
y	1	4	9	16	25	36	49	64	81

Пример №1:

Является ли графическим заданием какой-либо функции фигура?

Сколько бы мы не проводили вертикальных линий, всегда будет одно пересечение с графиком. Следовательно, изображенная фигура является графиком функции.

Пример №2:

Является ли графическим заданием какой-либо функции фигура?

Пример №3:

Является ли графическим заданием какой-либо функции фигура?

При проведении вертикальных линий у нас имеется два пересечения. То есть у одной вертикальной линии два пересечения с фигурой. По определению переменной x должно соответствовать только одно значение переменной y, а у нас два пересечения фигуры. Следовательно, данная фигура не является графиком функции.

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Функция – это отображение элементов множества X на множество Y . При этом каждому элементу x множества X соответствует одно единственное значение y множества Y .

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Графиком функции y = a x 2 + b x + c является парабола .

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :

Коэффициент a указывает на то, куда направлены ветки параболы.

Если a > 0 , ветки параболы направлены вверх.
Если a 0 , ветки параболы направлены вниз.

Коэффициент c указывает, в какой точке парабола пересекает ось y .
Коэффициент b помогает найти x в – координату вершины параболы.

Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

Если D > 0 – две точки пересечения.
Если D = 0 – одна точка пересечения.
Если D 0 – нет точек пересечения.

Графиком функции y = k x является гипербола .

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Функция y = x имеет следующий график:

Функция y = f ( x ) возрастает на интервале , если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале , если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции , находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции , находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

На этой странице мы постарались собрать для вас наиболее полную информацию об исследовании функции. Больше не надо гуглить! Просто читайте, изучайте, скачивайте, переходите по отобранным ссылкам.

Что будет дальше?

Общая схема исследования

Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены "горбы" выпуклости, где не определены значения и т.п.

А уже на основании этих "особенностей" и строится макет графика - картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).

Начнем, конечно же, с плана. Исследование функции - объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.

Алгоритм

Найти область определения. Выделить особые точки (точки разрыва).
Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
Найти точки пересечения с осями координат.
Установить, является ли функция чётной или нечётной.
Определить, является ли функция периодической или нет (только для тригонометрических функций).
Найти точки экстремума и интервалы монотонности.
Найти точки перегиба и интервалы выпуклости-вогнутости.
Найти наклонные асимптоты. Исследовать поведение на бесконечности.
Выбрать дополнительные точки и вычислить их координаты.
Построить график и асимптоты.

В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.

Схема исследования в формате pdf: скачать.

Полный пример решения онлайн

Провести полное исследование и построить график функции $$ y(x)=\frac. $$

1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя. $$1-x=0, \quad \Rightarrow \quad x=1.$$ Исключаем единственную точку $x=1$ из области определения функции и получаем: $$ D(y)=(-\infty; 1) \cup (1;+\infty). $$

2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:

Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ - вертикальная асимптота.

3) Определим точки пересечения графика функции с осями координат.

Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:

Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.

Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:

Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.

Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x \in (-\infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x \in (1; +\infty)$ функция $y\lt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).

4) Функция не является ни четной, ни нечетной, так как:

5) Исследуем функцию на периодичность. Функция не является периодической, так как представляет собой дробно-рациональную функцию.

6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:

Приравняем первую производную к нулю и найдем стационарные точки (в которых $y'=0$):

Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:

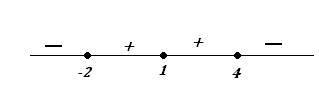
При $x \in (-\infty; -2), (4;+\infty)$ производная $y' \lt 0$, поэтому функция убывает на данных промежутках.

При $x \in (-2; 1), (1;4)$ производная $y' >0$, функция возрастает на данных промежутках.

При этом $x=-2$ - точка локального минимума (функция убывает, а потом возрастает), $x=4$ - точка локального максимума (функция возрастает, а потом убывает).

Найдем значения функции в этих точках:

Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.

7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:

Приравняем вторую производную к нулю:

Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x \in (-\infty; 1)$ выполняется $y'' \gt 0$, то есть функция вогнутая, когда $x \in (1;+\infty)$ выполняется $y'' \lt 0$, то есть функция выпуклая.

8) Исследуем поведение функции на бесконечности, то есть при .

Так как пределы бесконечны, горизонтальных асимптот нет.

Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:

Получили, у что функции есть одна наклонная асимптота $y=-x-1$.

9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.

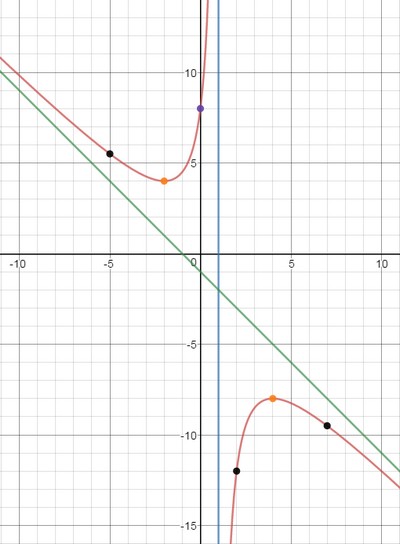
10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):

Примеры решений по исследованию функции

Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!

Задача 1. Исследовать функцию методами дифференциального исчисления и построить график.

Задача 2. Исследовать функцию и построить ее график.

Задача 3. Исследовать функцию с помощью производной и построить график.

Задача 4. Провести полное исследование функции и построить график.

Задача 5. Исследовать функцию методом дифференциального исчисления и построить график.

Задача 6. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.

Задача 7. Проведите исследование функции с построением графика.

Задача 8. Построить график функции $y=y(x)$, заданной параметрически

Задача 9. Исследовать функцию и построить ее график $r=1+tg \phi$.

Задача 10. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.

Задача 11. Провести полное исследование периодической функции $y = \cos 3x – 2 \sin 6x$ и построить её график.

Задача 12. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.

Задача 13. Провести полное исследование и построить график функции.

Как построить график онлайн?

Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).

Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?

Графический калькулятор Desmos

При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.

Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!

Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):

И такой график получается в итоге:

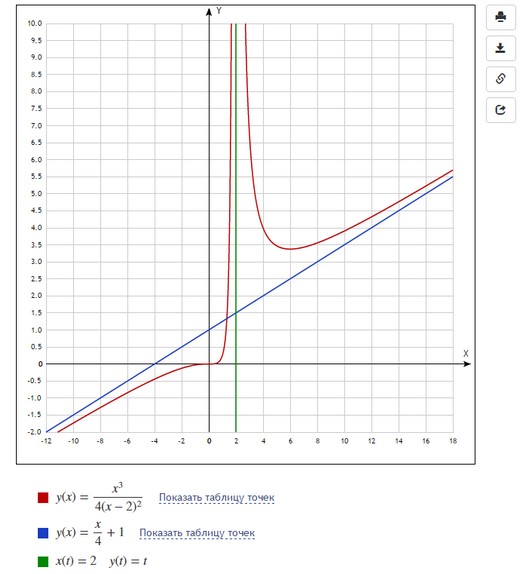
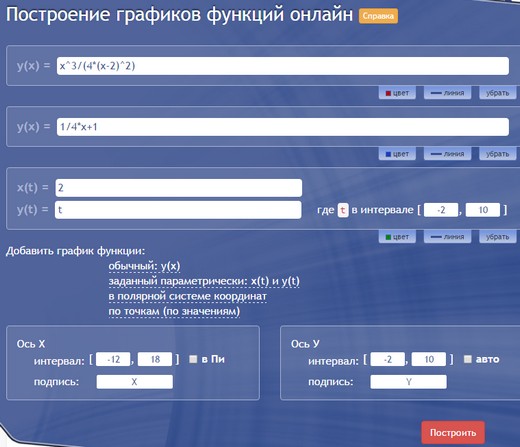
Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).

Другие сайты

Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:

Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой). Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл. При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа. Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет

Больше знаний: теория и практика

Еще немного ссылок для тех, кто хочет углубиться в тему. Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень "съедобно" даже для полного чайника в математике: Исследование функций от Александра Емелина.

Официальные инструкции, примеры и видео-инструкции на английском можно найти тут: Learn Desmos.

Решебник

Срочно нужна готовая задача? Более сотни разных функций с полным исследованием уже ждут вас. Подробное решение, быстрая оплата по SMS и низкая цена - около 50 рублей. Может, и ваша задача уже готова? Проверьте!

Полезные видео-ролики

Классный старый научно-популярный фильм "Математика. Функции и графики". Объяснения на пальцах в прямом смысле слова самых основ.

Сегодня публикуем четвёртую часть перевода руководства по JavaScript, которая посвящена функциям.

Функции в JavaScript

Поговорим о функциях в JavaScript, сделаем их общий обзор и рассмотрим подробности о них, знание которых позволит вам эффективно ими пользоваться.

Функция — это самостоятельный блок кода, который можно, один раз объявив, вызывать столько раз, сколько нужно. Функция может, хотя это и необязательно, принимать параметры. Функции возвращают единственное значение.

Функции в JavaScript являются объектами, если точнее, то они являются объектами типа Function . Их ключевое отличие от обычных объектов, дающее им те исключительные возможности, которыми они обладают, заключается в том, что функции можно вызывать.

Сначала рассмотрим особенности работы с функциями и соответствующие синтаксические конструкции, которые существовали в языке до появления стандарта ES6 и актуальны до сих пор.

Вот как выглядит объявление функции (function declaration).

Функцию можно назначить переменной или константе. Такая конструкция называется функциональным выражением (function expression).

Можно заметить, что в вышеприведённом примере функция назначена константе, но сама она имени не имеет. Такие функции называют анонимными. Подобным функциям можно назначать имена. В таком случае речь идёт об именованном функциональном выражении (named function expression).

Стрелочные функции, помимо того, что структуры, используемые для их объявления, получаются более компактными, чем при использовании обычных функций, отличаются от них некоторыми важными особенностями, о которых мы поговорим ниже.

Параметры функций

Параметры представляют собой переменные, которые задаются на этапе объявления функции и будут содержать передаваемые ей значения (эти значения называют аргументами). Функции в JavaScript могут либо не иметь параметров, либо иметь один или несколько параметров.

Здесь показано несколько примеров стрелочных функций.

Они представляют собой стандартные значения, задаваемые параметрам функций в том случае, если при её вызове значения некоторых параметров не задаются. Например, функцию, показанную выше, можно вызвать как с передачей ей всех двух принимаемых ей параметров, так и другими способами.

В ES8 появилась возможность ставить запятую после последнего аргумента функции (это называется trailing comma). Эта возможность позволяет повысить удобство редактирования кода при использовании систем контроля версий в ходе разработки программ. Подробности об этом можно почитать здесь и здесь.

Если функции нужно принимать много параметров, то запомнить порядок их следования может быть непросто. В таких случаях используются объекты с параметрами и возможности по деструктурированию объектов ES6.

Этот приём позволяет, описывая параметры в виде свойств объекта и передавая функции объект, получить в функции доступ к параметрам по их именам без использования дополнительных конструкций. Подробнее об этом приёме можно почитать здесь.

Значения, возвращаемые из функций

Все функции возвращают некое значение. Если команда возврата явно не задана — функция возвратит undefined .

Выполнение функции завершается либо после того, как оказывается выполненным весь код, который она содержит, либо после того, как в коде встречается ключевое слово return . Когда в функции встречается это ключевое слово, её работа завершается, а управление передаётся в то место, откуда была вызвана функция.

Если после ключевого слова return указать некое значение, то это значение возвращается в место вызова функции в качестве результата выполнения этой функции.

Из функции можно возвращать лишь одно значение. Для того чтобы получить возможность возврата нескольких значений, возвращать их можно либо в виде объекта, используя объектный литерал, либо в виде массива, а при вызове функции применять конструкцию деструктурирующего присваивания. Имена параметров при этом сохраняются. При этом, если нужно работать с объектом или массивом, возвращённым из функции, именно в виде объекта или массива, можно обойтись без деструктурирующего присваивания.

Вложенные функции

Функции можно объявлять внутри других функций.

Область видимости вложенной функции ограничена внешней по отношению к ней функцией, её нельзя вызвать извне.

Методы объектов

Когда функции используются в качестве свойств объектов, такие функции называют методами объектов.

Ключевое слово this

Если сравнить стрелочные и обычные функции, используемые в качестве методов объектов, можно обнаружить их важное различие, заключающееся в смысле ключевого слова this . Рассмотрим пример.

Как видно, вызов метода start() приводит ко вполне ожидаемому результату, а вот метод stop() явно работает неправильно.

Происходит это из-за того, что ключевое слово this по-разному ведёт себя при его использовании в стрелочных и обычных функциях. А именно, ключевое слово this в стрелочной функции содержит ссылку на контекст, включающий в себя функцию. В данном случае, если речь идёт о браузере, этим контекстом является объект window .

Вот как выглядит выполнение такого кода в консоли браузера.

Особенности ключевого слова this в обычных и стрелочных функциях

Как можно заметить, обращение к this в обычной функции означает обращение к объекту, а this в стрелочной функции указывает на window .

Всё это означает, что стрелочные функции не подходят на роль методов объектов и конструкторов (если попытаться использовать стрелочную функцию в роли конструктора — будет выдана ошибка TypeError ).

Немедленно вызываемые функциональные выражения

Немедленно вызываемое функциональное выражение (Immediately Invoked Function Expression, IIFE) — это функция, которая автоматически вызывается сразу после её объявления.

Точка с запятой перед IIFE необязательна, но её использование позволяет застраховаться от ошибок, связанных с автоматической расстановкой точек с запятой.

В вышеприведённом примере в консоль попадёт слово executed , после чего IIFE завершит работу. IIFE, точно так же как и другие функции, могут возвращать результаты своей работы.

После выполнения этого простого примера в консоль попадёт строка IIFE , которая оказалась в константе something после выполнения немедленно вызываемого функционального выражения. Может показаться, что особой пользы от такой конструкции нет. Однако если в IIFE выполняются некие сложные вычисления, которые нужно выполнить лишь однажды, после чего соответствующие механизмы оказываются ненужными — полезность IIFE оказывается очевидной. А именно, при таком подходе после выполнения IIFE в программе будет доступен лишь возвращённый функцией результат. Кроме того, можно вспомнить, что функции способны возвращать другие функции и объекты. Речь идёт о замыканиях, о них мы поговорим ниже.

Поднятие функций

Перед выполнением JavaScript-кода производится его реорганизация. Мы уже говорили о механизме поднятия (hoisting) переменных, объявленных с использованием ключевого слова var . Похожий механизм действует и при работе с функциями. А именно, речь идёт о том, что объявления функций в ходе обработки кода перед его выполнением перемещаются в верхнюю часть их области видимости. В результате, например, оказывается, что вызвать функцию можно до её объявления.

Если переместить вызов функции так, чтобы он шёл после её объявления, ничего не изменится.

Если же в похожей ситуации воспользоваться функциональным выражением, то похожий код выдаст ошибку.

Стрелочные функции

Сейчас мы подробнее поговорим о стрелочных функциях, с которыми мы уже встречались. Их можно считать одним из наиболее значительных новшеств стандарта ES6, они отличаются от обычных функций не только внешним видом, но и особенностями поведения. В наши дни они используются чрезвычайно широко. Пожалуй, нет ни одного современного проекта, где они не использовались бы в подавляющем большинстве случаев. Можно сказать, что их появление навсегда изменило и внешний вид JS-кода и особенности его работы.

С чисто внешней точки зрения синтаксис объявления стрелочных функций оказывается компактнее синтаксиса обычных функций. Вот объявление обычной функции.

Вот объявление стрелочной функции, которое, в целом, если не учитывать особенности стрелочных функций, аналогично предыдущему.

Если тело стрелочной функции содержит лишь одну команду, результат которой возвращает эта функция, его можно записать без фигурных скобок и без ключевого слова return . Например, такая функция возвращает сумму переданных ей аргументов.

Как видите, параметры стрелочных функций, как и в случае с обычными функциями, описывают в скобках. При этом, если такая функция принимает всего один параметр, его можно указать без скобок. Например, вот функция, которая возвращает результат деления переданного ей числа на 2.

В результате оказывается, что стрелочные функции очень удобно использовать в ситуациях, в которых нужны маленькие функции.

▍Неявный возврат результатов работы функции

Мы уже касались этой особенности стрелочных функций, но она настолько важна, что её следует обсудить подробнее. Речь идёт о том, что однострочные стрелочные функции поддерживают неявный возврат результатов своей работы. Пример возврата примитивного значения из однострочной стрелочной функции мы уже видели. Как быть, если такая функция должна возвратить объект? В таком случае фигурные скобки объектного литерала могут запутать систему, поэтому в теле функции используются круглые скобки.

▍Ключевое слово this и стрелочные функции

Выше, когда мы рассматривали особенности ключевого слова this , мы сравнивали обычные и стрелочные функции. Этот раздел призван обратить ваше внимание на важность их различий. Ключевое слово this , само по себе, может вызывать определённые сложности, так как оно зависит и от контекста выполнения кода, и от того, включен или нет строгий режим (strict mode).

Как мы уже видели, при использовании ключевого слова this в методе объекта, представленного обычной функцией, this указывает на объект, которому принадлежит метод. В таком случае говорят о привязке ключевого слова this к значению, представляющему собой контекст выполнения функции. В частности, если функция вызвана в виде метода объекта, то ключевое слово this привязано к этому объекту.

В случае же со стрелочными функциями оказывается так, что в них привязка this не выполняется, они пользуются ключевым словом this из содержащих их областей видимости. В результате их не рекомендуется использовать в качестве методов объектов.

Та же самая проблема возникает и при использовании функций в качестве обработчиков событий элементов DOM. Например, HTML-элемент button используют для описания кнопок. Событие click вызывается при щелчке мышью по кнопке. Для того чтобы отреагировать на это событие в коде, нужно сначала получить ссылку на соответствующий элемент, а потом назначить ему обработчик события click в виде функции. В качестве такого обработчика можно использовать и обычную функцию, и стрелочную. Но, если в обработчике событий нужно обращаться к тому элементу, для которого оно вызвано (то есть — к this ), стрелочная функция тут не подойдёт, так как доступное в ней значение this указывает на объект window . Для того чтобы проверить это на практике, создайте HTML-страницу, код которой показан ниже, и понажимайте на кнопки.

В данном случае при нажатии на эти кнопки будут появляться окна, содержащие true . Однако в обработчике события click кнопки с идентификатором fn проверяется равенство this самой кнопке, а в кнопке с идентификатором arrowFn проверяется равенство this и объекта window .

В результате, если в обработчике события HTML-элемента нужно обращаться к this , стрелочная функция для оформления такого обработчика не подойдёт.

Замыкания

Замыкания — это важная концепция в JavaScript. Фактически, если вы писали JS-функции, то вы пользовались и замыканиями. Замыкания применяются в некоторых паттернах проектирования — в том случае, если нужно организовать строгий контроль доступа к неким данным или функциям.

Когда функция вызывается, у неё есть доступ ко всему тому, что находится во внешней по отношению к ней области видимости. Но к тому, что объявлено внутри функции, извне доступа нет. То есть, если в функции была объявлена некая переменная (или другая функция), они недоступны внешнему коду ни во время выполнения функции, ни после завершения её работы. Однако если из функции возвратить другую функцию, то эта новая функция будет иметь доступ ко всему тому, что было объявлено в исходной функции. При этом всё это будет скрыто от внешнего кода в замыкании.

Рассмотрим пример. Вот функция, которая принимает имя собаки, после чего выводит его в консоль.

Значение, возвращаемое этой функцией нас пока не интересует, текст выводится в консоль с помощью IIFE, что в данном случае особой роли не играет, однако, это поможет нам увидеть связь между этой функцией и её вариантом, в котором, вместо вызова функции, которая выводит текст в консоль, мы эту функцию из переписанной функции bark() возвратим.

Результат работы код в двух случаях оказывается одинаковым. Но во втором случае то, что было передано исходной функции при её вызове (имя собаки, Roger ), хранится в замыкании, после чего используется другой функцией, возвращённой из исходной.

Проведём ещё один эксперимент — создадим, пользуясь исходной функцией, две новых, для разных собак.

Этот код выведет следующее.

Оказывается, что значение константы say привязано к функции, которая возвращена из функции prepareBark() .

Обратите внимание на то, что say , при повторном вызове prepareBark() , получает новое значение, при этом значение, записанное в say при первом вызове prepareBark() , не меняется. Речь идёт о том, что при каждом вызове этой функции создаётся новое замыкание.

Итоги

Сегодня мы говорили об обычных и стрелочных функциях, об особенностях их объявления и использования, о том, как, в разных ситуациях ведёт себя ключевое слово this , и о замыканиях. В следующий раз обсудим массивы и циклы.

Что такое функции, области определения и значений функции

Функция — вид зависимости, при котором каждому элементу одного множества ставится в соответствие элемент другого множества.

В общем виде функцию в алгебре обозначают как y=f(x). Переменную x называют независимой переменной или аргументом функции, переменную y — зависимой переменной или значением функции.

Основными характеристиками функции являются:

область определения;
область значений.

Область определения — множество значений, которые может принимать аргумент функции, то есть переменная x. Область определения иногда называют областью допустимых значений. Обозначение области допустимых значений функции f: D (f).

Также область определения можно трактовать как проекцию графика функции на ось абсцисс.

Областью значений называется множество всех значений функции (переменной y), полученных при переборе всех значений переменной x из области определения. Принято следующее обозначение области значений: E (f).

В графическом изображении область значений — проекция графика функции на ось ординат.

Нахождение области значений осуществляется одним из следующих способов:

графически;
аналитически (по уравнению).

Способы нахождения области значений некоторых функций по графику

Чаще всего графический способ используют для функций с достаточно простой зависимостью. В этом случае построение графика не вызывает трудностей.

Приведем алгоритм нахождения области значений функции по графику:

Как найти область значений функции по уравнению

Нахождение области значений функции по заданному уравнению также сводится к вычислению экстремумов.

Рассмотрим два случая:

Нахождение области значений функции, непрерывной на некотором заданном отрезке.
Нахождение области значений функции, непрерывной на некотором интервале. Сюда же отнесем случаи, когда функция не существует в какой-либо точке. Например, точка нуля знаменателя, в которой функция не существует, а область определения терпит разрыв.

Алгоритм поиска области значений для первого случая:

Для второго случая:

Находим производную, приравниваем ее к нулю и определяем знаки производной на каждом промежутке.
Определяем значение функции в каждой из точек. Для определения значения функции в граничных точках, а также в точках разрыва или точках, в которых производная не существует, вычисляем пределы функции аналогично указанным в пункте 5 для первого случая.
Определяем и записываем область значений.

Примеры решений

Рассмотрим несколько примеров на нахождение области значений функции и приведем их решения.

Найти область значений функции y = x по графику.

Найдем область определения функции. Выражение под знаком квадратного корня всегда положительно, то есть x≥0, и область определения D(f(x))=[0; +∞). Теперь построим график функции.

Из графика видно, что минимальное значение переменная y принимает при x=0. Максимальное значение не определяется, при этом видно, что при возрастании x значении y также растет. Получили, что y m i n = 0 , а область значений E(f(x))=[0; +∞).

Найти область значений функции y = 4 x x 2 + 2 на отрезке [-2; 2].

Найдем область определения функции. Функция представляет собой дробь, однако, ее знаменатель не будет равен нулю при любых значениях x. Действительно, квадрат любого числа есть положительное число, получили в знаменателе сумму положительных чисел. Тогда D=R, где R — множество действительных чисел.

Найдем производную функции: y ' ( x ) = 4 x x 2 + 2 ' = 4 ( 2 - x 2 ) ( x 2 + 2 ) 2 .

Приравняем числитель производной к нулю и найдем корни получившегося уравнения: 8 - 4 x 2 = 0 ; x 1 = - 2 и x 2 = 2 .

Отметим корни на координатной оси и, поочередно подставляя значения x = - 4 , - 2 , 2 , 4 , определим знаки производной на каждом промежутке.

Из рисунка видно, что функция имеет один минимум и максимум. Вычислим значения y m i n и y m a x :

y m i n = y ( - 2 ) = 4 · ( - 2 ) ( - 2 ) 2 + 2 = - 2 ;

y m a x = y ( 2 ) = 4 · ( 2 ) ( 2 ) 2 + 2 = 2 .

Экстремумы функции входят в заданный интервал и не являются точками разрыва области определения функции, то есть минимальные и максимальные значения должны быть включены в область значений.

Ответ: E ( f ( x ) ) = [ - 2 ; 2 ] .

Найти область значений функции y = 5 x + 1 на области действительных чисел.

Найдем область определения функции. Знаменатель не может быть равным нулю, значит, D ( f ( x ) ) = ( - ∞ ; - 1 ) U ( - 1 ; + ∞ ) .

Найдем производную: y ' ( x ) = - 5 ( x + 1 ) 2 .

Получили, что производная не равна нулю при любых x. При x=-1 знаменатель производной обращается в ноль, то есть в данной точке производная не существует.

Отметим точку x=-1 и рассмотрим два промежутка: (-∞;-1) и (-1;+∞).

Определим знаки производной на каждом промежутке.

Из рисунка видно, что функция убывает на обоих интервалах и не имеет максимума или минимума.

Теперь определим значение функции в точке x=-1, для чего вычислим пределы функции при x→-1-0 и x→-1+0.

lim x → ( - 1 - 0 ) 5 x + 1 = 5 - 1 - 0 + 1 = 5 - 0 = - ∞ ;

lim x → ( - 1 + 0 ) 5 x + 1 = 5 - 1 + 0 + 1 = 5 + 0 = + ∞ .

Итак, точка x=-1 — это точка разрыва второго рода.

Значение функции на границах заданного интервала -∞ и +∞ также вычисляется с помощью пределов:

Читайте также: