Как сделать уравнение с остатком

Добавил пользователь Alex
Обновлено: 04.10.2024

В данной публикации мы рассмотрим теорему Безу, с помощью которой можно найти остаток от деления многочлена на двучлен, а также, научимся применять ее на практике для решения примеров.

Формулировка теоремы Безу

Остаток от деления многочлена P(x) на двучлен (x-a) равняется P(a) .

Следствие из теоремы:

Число a является корнем многочлена P(x) исключительно в том случае, если многочлен P(x) без остатка делится на двучлен (x-a) .

Из этого следствия вытекает следующее утверждение: множество корней многочлена P(x) тождественно множеству корней соответствующего уравнения P(x)=0 .

Решение примеров

Пример 1
Найдите остаток от деления многочлена 5x 2 – 3x + 7 на двучлен (x – 2) .

Решение
Чтобы найти остаток от деления, согласно теореме Безу, требуется найти значение многочлена в точке a (т.е. вместо x подставляем значение a , которое в нашем случае равняется числу 2).
5 ⋅ 2 2 – 3 ⋅ 2 + 7 = 21 .

Т.е. остаток равен 21.

Пример 2
Используя теорему Безу выясните, делится ли многочлен 3x 4 + 15x – 11 на двучлен (x + 3) без остатка.

Решение
В данном случае a = -3 . Подставляем это число вместо x в многочлен и получаем:
3 ⋅ (-3) 4 + 15 ⋅ (-3) – 11 = 187 .

Это значит, что деление без остатка невозможно.

Пример 3
Выясните, при каком значении y , многочлен x 23 + yx + 16 без остатка делится на двучлен (x + 1) .

Решение
Применив теорему Безу, находим нулевой остаток от деления:
(-1) 23 + y ⋅ (-1) + 16 = 0
-1 – y + 16 = 0
y = 15

Таким образом, при y , равном 15, остаток будет равен 0.

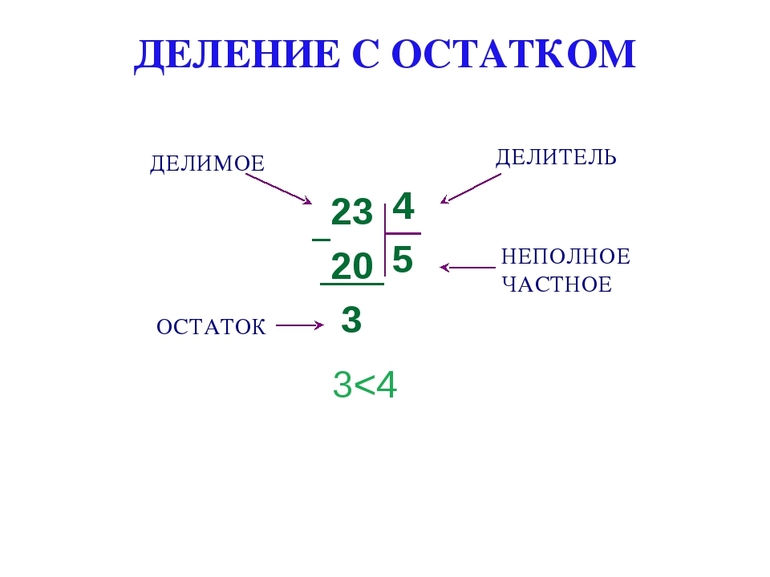
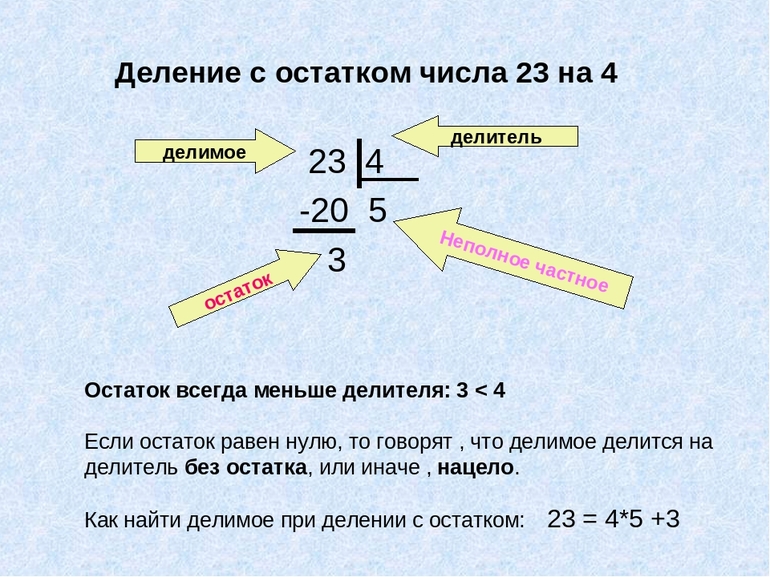
Разделить с остатком число a на число b - значит найти два таких числа: c - частное и n - остаток, и сложить их.

Данную формулу так же можно прочитать следующим образом:

Разделить с остатком число a на число b - значит найти два таких числа c и n (частное и остаток), что:

Правило деления с остатком

Что бы разделить число с остатком, нужно:

1. Подобрать близкое к делимому число, которое меньше делимого и делителя на делитель без остатка;

3. Найти остаток - из делимого вычесть число, которое разделили. Остаток всегда должен быть меньше делителя.

19 : 4 = 4 (остаток 1), 19 = 4 • 4 + 3;

Объясним правило на примере 19 : 4

1. Подбираем близкое к 19 число, которое меньше 19 и делится на 4 без остатка. Это число 16;

В математике встречаются примеры деления с остатком. В 5 классе подробно изучается методика выполнения этой операции, однако для этого нужны определенные базовые знания. Для их получения необходимо изучить теорию, основанную на признаках делимости двух числовых величин. После ознакомления с правилами специалисты рекомендуют переходить непосредственно к практике.

Общие сведения
Классификация числовых величин
Правила целочисленного частного
Определение принадлежности чисел
Методика деления с остатком
Пример решения

Общие сведения

Деление с остатком используется практически во всех дисциплинах с физико-математическим направлением. Операция позволяет записывать значения с выделением целой части. Одним из направлений является программирование. В этой дисциплине используются различные алгоритмы, работа которых основана на этом виде деления.

Следует отметить, что для выполнения этой операции существует определенная методика. Однако для ее реализации необходимы начальные знания. К ним относятся следующие:

Понятие о частном.
Правила делимости двух величин.

Операция частного состоит из трех элементов: делимого q, делителя p и их результата r. Выражение в математической форме имеет такой вид: q/p=r или q: p=r. Далее необходимо разобрать определение каждого компонента.

Делимое — числовое значение, которое нужно разделить на один из сомножителей. Делитель — один из множителей, на которые делится величина делимого. Результат операции называется частным двух или более чисел. Следует отметить, что деление классифицируется на два вида: без остатка и с его наличием.

Классификация числовых величин

Признаки делимости — отдельные критерии, при помощи которых можно сделать вывод о целочисленном делении одной величины на другую. Следует отметить, что числа классифицируются на два вида:

Для определения первых нужно воспользоваться тремя методами: специальными таблицами, средствами вычислительной техники и расчетным способом. В каждом учебнике по математике находятся в дополнениях таблица простых чисел. Кроме того, в интернете можно загрузить специальные программы, позволяющие определить принадлежность значения к простой величине.

Последний метод называется ручным, поскольку для определения принадлежности к этой группе необходимо воспользоваться признаками делимости. Отличительной особенностью простого значения от составного является возможность осуществления операции деления нацело только на единицу или само себя. Составные величины включают другие множители, отличные от единицы и эквивалентного значения.

Специалисты рекомендуют занести признаки делимости на специальные карточки, сделанные из картона. На них необходимо разборчиво написать все правила целочисленного деления двух чисел. Начинающие математики, которые стремятся добиться больших успехов в этой дисциплине, должны придумать примеры к каждому, как это сделано для семерки.

Правила целочисленного частного

В учебнике советского математика Виленкина Наума Яковлевича, одобренном Федеральными государственными образовательными стандартами (ФГОС), можно найти правила делимости нацело одного значения на другое. К ним относятся следующие:

На единицу и эквивалентное значение делится любая величина.
Только четные значения, последний разряд которых заканчивается на цифры 2, 4, 6, 8, 0, могут делиться на двойку.
Если сумма всех элементов разрядной сетки делится на тройку, то значит частное при делении на это значение будет целым.
На четверку можно разделить величину, у которой сумма разрядов единиц и десятков делится на четыре.
Условие деления на 5 — разряд единиц эквивалентен 0 или 5.
Чтобы разделить искомое значение на шесть, необходимо соблюдение сразу двух условий (второго и третьего).
Для деления величины, количество разрядов которой превышает 7, на семерку необходимо руководствоваться таким методом: разбить на группы-триады (по три), а затем просуммировать. Сумма должна делиться на 7. Если количество цифр не превышает 7, то нужно отсеять последний единичный элемент, и отнять от искомого числа удвоенный последний компонент. Результат должен делиться на 7.
Условием деления величины на восьмерку является одновременное выполнение второго и четвертого правил.
Чтобы разделить значение на 9, необходимо сложить все компоненты разрядной сетки. Результирующая величина при этом должна быть целочисленным значением.
Когда последний разряд равен нулю, тогда число делится на 10.

Однако седьмое правило может показаться не совсем понятным для начинающих математиков. В этом случае необходимо разобрать более подробно его реализацию на примере числа 754231897. Решение выполняется таким образом:

Разбить на триады начиная от единиц: 754 | 231 | 897.
Сложить элементы в группах: 18+6+24=48.
Результат, полученный на втором шаге, не делится на 7 по таблице умножения (49/7=7 и 56/7=8).

Если величина имеет меньшее количество разрядов (273), то формула определения записывается таким образом: 27−2*3=27−9=21. На основании полученного результата можно сделать вывод о том, что частное чисел 273 и 7 является целой величиной.

Определение принадлежности чисел

Не во всех случаях можно воспользоваться программным обеспечением, предварительно инсталлированным на телефон или компьютер. Для этого специалисты рекомендуют использовать методику определения принадлежности числа к группе простых или составных величин. Она имеет такой вид:

Написать исходную величину.
Найти ее множители, основываясь на правила делимости.

Однако для демонстрации работы алгоритма необходимо выполнить анализ для величины, эквивалентной 567. Реализация имеет следующий вид (номер шага равен делителю, кроме первого):

Далее нахождение множителей можно не продолжать. Исключение составляют только задачи, в которых необходимо найти все делители. Теперь можно переходить непосредственно к алгоритму деления с остатком, поскольку базовых знаний уже достаточно для выполнения этой операции.

Методика деления с остатком

Результатом операции нахождения частного двух чисел может быть целочисленной или дробное значение. В основном реализация их алгоритмов совпадает. Следовательно, необходимо рассмотреть один из них. Рекомендуется подробно разобрать пример на деление без остатка для 5 класса. Методика имеет следующий вид:

Написать число и делитель: 542/2.
Взять старший разряд: 5.
Разделить его на делитель, выделив целую часть и остаток (записывается в скобках): 5/2=2 (+1). В результирующую графу записать 2.
Перемножить частное (2) и делитель (2), записав под старшей группой результат их произведения: 2*2=4.
От 5 отнять 4: 5−4=1.
Снести разряд десятков, поставив его рядом с 1: 14.
Разделить величину в шестом пункте на делитель: 14/2=7 (записать к частному).
Вынести последний элемент разрядной сетки, поделив его на 2: 2/2=1 (записать в графу результата).
Ответ: 271.
Выполнить проверку при помощи калькулятора: 271*2=542.

Можно составить задание, какое позволит применить этот алгоритм, но результат получится с остатком. Для этого необходимо решать задачу для нечетного числа и двойки, т. е. 541/2.

Нахождение частного осуществляется таким образом:

Кроме того, эту методику также рекомендуется записать на отдельном листе бумаги. Она должна быть перед глазами, поскольку необходимо сформировать правильные действия учащегося при решении задач этого типа. Со временем ее можно будет убрать.

Пример решения

Специалисты рекомендуют также решать задачи на деление с остатком для 5 класса. Это связано с тем, что для лучшего результата недостаточно просто проходить школьный материал, а необходимо составлять различные задания. Одно из них имеет условие следующего вида:

Известен делитель и остаток: 3 и 2 соответственно.
Число-делимое состоит из трех разрядов, сумма которых эквивалентна 17.
Разряд сотен меньше десятков в 2 раза, а третий элемент меньше их суммы на 1.
Частное состоит из трех разрядов, десятки и единицы которого равны, а сотня на 1 меньше любого из них.
Необходимо найти делимое.

Математики рекомендуют решить задание самостоятельно, а затем сопоставить ответы. Оно решается по такой методике:

Составляются уравнения (t — первый старший разряд, s — десятки и u — единицы): s=2t, u=t+2t-1, t+2t+(t+2t-1)=17.
Корни последнего уравнения: t=3. Отсюда s=6 и u=8.
Искомое число: 368.

Если подставить величины, которые получились во втором пункте, то можно сделать вывод о правильном нахождении значения. Оно состоит из трех разрядов, т. е. 368. Сумма последних составляет 17, что удовлетворяет условию задачи (3+6+8=17). Компонент, находящийся в разрядной сетке на месте сотен, меньше элемента разряда десятков в два раза, т. е. 6/3=2. Последняя цифра вычисляется по формуле: сотни+десятки-единицы=3+6−8=1.

Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.

Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.

Деление натуральных чисел столбиком с остатком

Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.

Приведем решение примера, так как понять суть метода проще всего на практике.

Пример 1. Как делить натуральные числа с остатком?

Разделим натуральное число 273844 на натуральное число 97 .

Проводим деление столбиком и записываем:

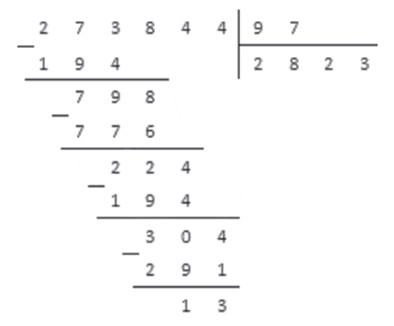
Результат: неполное частное от деления равно 2823 , а остаток равен 13 .

Деление чисел с остатком через последовательное вычитание

Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.

Пример 2. Деление с остатком через последовательное вычитание.

Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3 .

Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7 - 3 = 4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет. Остается 4 - 3 = 1 яблоко.

1 яблоко - это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:

7 ÷ 3 = 2 (остаток 1)

Это значит, что число 3 как бы умещается в числе 7 два раза, а единица - остаток, меньший чем 3 .

Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.

Пример 3. Деление с остатком через последовательное вычитание.

Вычислим: 145 ÷ 46 .

Число 99 больше, чем 46 , поэтому продолжаем последовательное вычитание делителя:

Повторяем эту операцию еще раз:

В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток - результат вычитания, который меньше делителя. В нашем случае остатком является число 7 .

145 ÷ 46 = 3 (остаток 7) .

Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.

Если a b , то a ÷ b = 0 (остаток a) .

12 ÷ 36 = 0 (остаток 12) 47 ÷ 88 = 0 (остаток 47)

Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.

Метод подбора неполного частного

При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.

Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1 , 2 , 3 и т.д.

Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение d = a - b · c . Здесь d - остаток от деления, a - делимое, b - делитель, с - неполное частное.

В-третьих, не будем забывать, что остаток всегда меньше делителя.

Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0 , 1 , 2 , 3 и т.д. Применяя формулу d = a - b · c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b . Число, взятое за с на этом шаге и будет неполным частным.

Разберем применение этого метода на примере.

Пример 4. Деление с остатком методом подбора

Разделим 267 на 21 .

a = 267 ; b = 21 . Подберем неполное частное.

Используем формулу d = a - b · c и будем последовательно перебирать c , придавая ему значения 0 , 1 , 2 , 3 и т.д.

Если с = 0 , имеем: d = a - b · c = 267 - 21 · 0 = 267 . Число 267 больше, чем 21 , поэтому продолжаем подстановку.

При с = 1 имеем: d = a - b · c = 267 - 21 · 1 = 246 . Т.к. 246 > 21 , снова повторяем процесс.

При с = 2 имеем: d = a - b · c = 267 - 21 · 2 = 267 - 42 = 225 ; 225 > 21 .

При с = 3 имеем: d = a - b · c = 267 - 21 · 3 = 267 - 63 = 204 ; 204 > 21 .

При с = 12 имеем: d = a - b · c = 267 - 21 · 12 = 267 - 252 = 15 ; 15 21 .

На этом этапе процесс деления можно считать законченным. Неполное частное с = 12 , а остаток деления равен 15 .

Алгоритм деления натуральных чисел с остатком

Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.

Вспомним, что в случае, когда a b, неполное частное равно нулю, а остаток равен делимомому a . Мы будем рассматривать случай, когда a > b .

Сформулируем три вопроса и ответим на них:

Что там известно?
Что нам нужно найти?
Как мы будем это делать?

Изначально известными являются делимое и делитель: a и b .

Найти нужно неполное частное c и остаток d .

Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a = b · c + d . Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a = b · c + d , тогда мы найдем искомые величины.

Алгоритм деления, благодаря которому мы представим a в виде суммы a = b · c + d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47 .

1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе - два.

Запомним это число.

2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.

В нашем примере справа от 47 дописываем нуль. Так как 470 899 , запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число 1 так и остается у нас в памяти.

3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10 . В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.

4. Будем последовательно умножать делитель на 1 , 2 , 3 . . и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.

Рабочий разряд в нашем примере - десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470 .

470 899 , поэтому умножаем на еще одну единицу рабочего разряда. Получаем: 47 · 20 = 940 ; 940 > 899 .

Число, которое мы получили на предпоследнем шаге ( 470 = 47 · 10 ) является первым из искомых слагаемых.

5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.

Шаги 1 - 5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1 - 5 , но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.

Обратимся к примеру. 899 - 470 = 429 , 429 > 47 . Повторяем шаги 1 - 5 алгоритма с числом 429 , взятым в качестве делимого.

1. В записи числа 429 на один знак больше, чем в записи числа 47 . Запоминаем разницу - число 1 .

2. В записи делимого справа дописываем один нуль. Получаем число 470 . Так как 470 > 429 , из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1 - 1 = 0 . Запоминаем 0 .

3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы

4. Последовательно умножим делитель 47 на 1 , 2 , 3 . . и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47 · 9 = 423 429 , 47 · 10 = 470 > 429 . Таким образом, второе искомое слагаемое - 47 · 9 = 423 .

5. Разность между 429 и 423 равна числу 6 . Так как 6 47 , это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком.

6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899 = 470 + 423 + 6 . Вспоминаем, что 470 = 47 · 10 , 423 = 47 · 9 . Перепишем равенство:

899 = 47 · 10 + 47 · 9 + 6

Применим распределительное свойство умножения.

899 = 47 · 10 + 47 · 9 + 6 = 47 · ( 10 + 9 ) + 6

Таким образом, мы представили делимое в виде уже данной ранее формулы a = b · c + d .

Искомые неизвестные:неполное частное с = 19 , остаток d = 6 .

Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:

Пример 5. Деление натуральных чисел с остатком

Разделим числа 42252 и 68 .

Используем алгоритм. Первые пять шагов дают первое слагаемое - число 40800 = 68 · 600 .

Снова повторяем первые пять шагов алгоритма с числом 1452 = 42252 - 40800 и получаем второе слагаемое 1360 = 68 · 20

Третий раз проходим шаги аглоритма, но у же с новым числом 92 = 1452 - 1360 . Третье слагаемое равно 68 = 68 · 1 . Остаток равен 24 = 92 - 68 .

В результате получаем:

42252 = 40800 + 1360 + 68 + 24 = 68 · 600 + 68 · 20 + 68 · 1 + 24 = = 68 · ( 600 + 20 + 1 ) + 24 = 68 · 621 + 24

Неполное частное равно 621 , остаток равен 24 .

Деление натуральных чисел с остатком. Проверка результата

Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.

На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.

Остаток всегда меньше делителя!

На втором этапе проверяется справедливость равенства a = b · c + d . Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.

Пример 6. Проверка результата деления натуральных чисел с остатком.

Проверим, верно ли, что 506 ÷ 28 = 17 (остаток 30) .

Сравниваем остаток и делитель: 30 > 28 .

Значит, деление выполнено неверно.

Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5 . Правильно ли он сделал?

Чтобы узнать это, сначала сравниваем остаток и делитель: 5 13 .

Первый пункт проверки пройден, переходим ко второму.

Запишем формулу a = b · c + d . a = 121 ; b = 13 ; c = 9 ; d = 5 .

Подставляем значения и сравниваем результаты

13 · 9 + 5 = 117 + 5 = 122 ; 121 ≠ 122

Значит, в вычисления школьника где-то закралась ошибка.

Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111 . В результате у него получилось число 54 с остатком 4 . Все ли правильно посчитано?

Проверим! Остаток 4 меньше, чем делитель 111 , поэтому переходим ко второму этапу проверки.

Используем формулу a = b · c + d , где a = 5998 ; b = 111 ; c = 54 ; d = 4 .

Читайте также: