Как сделать уравнение окружности

Обновлено: 05.07.2024

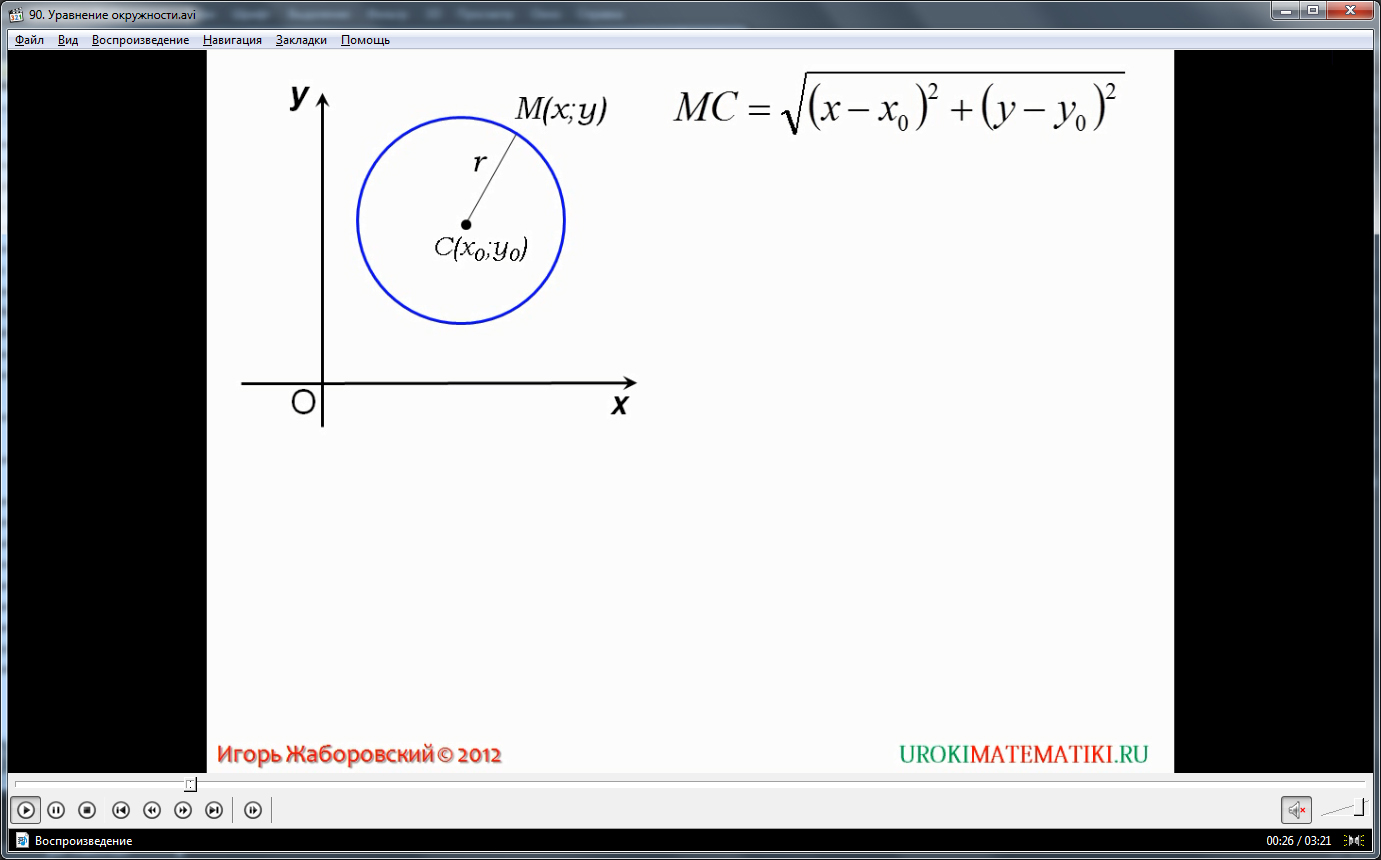
Окружностью принято обозначать множество всех точек плоскости , равноудаленных от одной точки – от центра.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, $\mathrm$ – гипербола.

Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.

Все записанные выражения являются уравнениями с двумя переменными.
В общем случае их принято записывать в виде F(x; y) = 0.

Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = $\mathrm$ – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график - ниже).

п.2. Обобщенные правила преобразования графика уравнения

Пусть F(x; y) = 0 – исходный график некоторой функции

Преобразование

Симметричное отображение относительно оси OY

Симметричное отображение относительно оси OX

Центральная симметрия относительно начала координат

F(x – a; y) = 0
a > 0

Параллельный перенос графика на a единиц вправо

F(x + a; y) = 0
a > 0

Параллельный перенос графика на a единиц влево

F(x; y – b) = 0
b > 0

Параллельный перенос графика на b единиц вниз

F(x; y + b) = 0
b > 0

Параллельный перенос графика на b единиц вверх

F(ax; y) = 0
a > 1

Сжатие графика к оси OY в a раз

F(ax; y) = 0
0 1

Сжатие графика к оси OX в b раз

F(x; by) = 0
0 Например:

Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ \mathrm $$

п.4. Примеры

Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: $ \mathrm=-\frac + 2 > $ – это прямая

б) xy + 4 = 0
Выразим y из уравнения: $ \mathrm> $ – это гипербола

в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом $ \mathrm=2> $

г) x 2 + 5y – 2 = 0
Выразим y из уравнения: $ \mathrm> $ – это парабола

Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
$ \mathrm=-\frac25|x|+2> $
Строим график для $ \mathrm $, а затем отражаем его относительно оси OY в левую полуплоскость.

б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.

в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.

г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).

д) $\mathrm<\frac<|x-1|>+2|y-2|=4>$
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.

Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A₁A₂| 2 =
= ( x₂ – x₁) 2 + ( y₂ – y₁) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

В ходе видеоурока используются следующие эффекты – анимация, структурирование материала по кадрам, выделение цветом важных понятий и деталей построения и теоретической части. Видеоуроки помогают сконцентрировать внимание учеников на изучении темы. Структурированная, четкая подача материала улучшает его восприятие. Последовательное объяснение с построением, голосовым сопровождением дает возможность улучшить усвоение материала учениками с различными способностями и особенностями внимания.

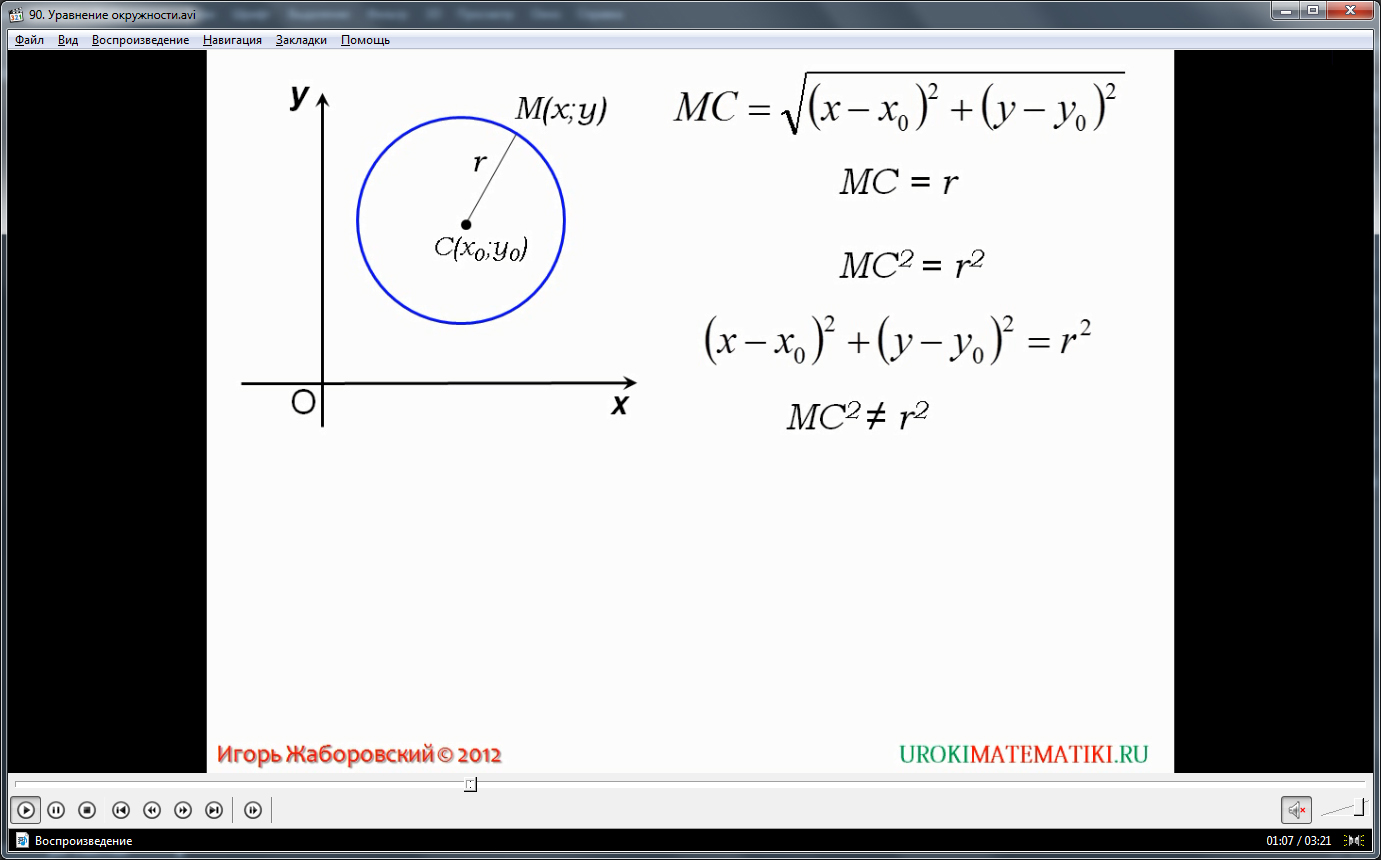
Видеоурок начинается с представления темы урока. На экране строится прямоугольная система координат, на которой нарисована окружность с центром в точке С(х₀;у₀). Также в данной окружности отмечен радиус r. По известным свойствам окружности расстояние между ее центром и любой точкой М(х;у), принадлежащей окружности, будет вычисляться по формуле, уже изученной на прошлых уроках. Соответственно, расстояние между точкой М(х;у) и С(х₀;у₀) будет представлено формулой МС=√(х-х₀) 2 +(у-у₀) 2 . Так как данное расстояние в окружности представлено радиусом, верно равенство МС=r. Возведя в квадрат обе части равенства, получим МС 2 =r 2 . Подставив вместо МС выражение, отражающее расстояние между точками в системе координат, получаем (х-х₀) 2 +(у-у₀) 2 = r 2 . Также отмечается, что данное уравнение не будет верно для любой другой точки, которая лежит вне данной окружности. Из рассуждения делается вывод, что уравнение окружности, имеющей радиус r и центр в точке С(х₀;у₀) в прямоугольной системе координат выражается следующим равенством (х-х₀) 2 +(у-у₀) 2 = r 2 .

Отдельно выведено уравнение окружности, центр которой располагается в начале координат. В этом случае координаты центра окружности равны нулю. Уравнение окружности преобразуется в вид х 2 +у 2 = r 2 .

Для усвоения рассмотренного материала приводится пример нахождения уравнения окружности. В примере необходимо описать уравнение окружности, которая проходит через начало координат, а центр имеет в точке (-3;4). Зная, что центр окружности располагается в точке (-3;4), записываем уравнение, пользуясь изученной формулой (х+3) 2 +(у-4) 2 = r 2 . Чтобы определить радиус окружности r, необходимо воспользоваться заданным условием, что окружность проходит через начало координат. Чтобы определить радиус, подставляем значение координат данной точки в уравнение (0+3) 2 +(0-4) 2 = r 2 . После вычислений получаем r 2 =25. Вычисленный радиус окружности r=5. В результате анализа получаем готовое уравнение окружности (х+3) 2 +(у-4) 2 = 25. Данное уравнение после раскрытия скобок принимает вид х 2 +у 2 +6х-8у=0. Данное уравнение также является уравнением окружности.

Читайте также: