Как сделать таблицу конечных разностей

Добавил пользователь Евгений Кузнецов
Обновлено: 05.10.2024

Конечные разности. Пусть известны значения некоторой функции для равноотстоящих значений аргумента . Конечными разностями первого порядка называются следующие величины:

Aналогично определяются конечные разности второго порядка:

Конечные разности -го порядка выражаем через конечные разности -го порядка: ; ; …; ; … .

Вычисление конечных разностей можно оформить в виде
табл. 7.1, которая называется диагональной таблицей конечных разностей.

Первая интерполяционная формула Ньютона. Интерполяционный полином Ньютона – форма записи интерполяционного полинома P_n(x), которая допускает уточнения результатов интерполирования последовательным прибавлением новых узлов.

Первая интерполяционная формула Ньютона имеет вид

Формула используется для интерполирования в точках , близких к началу таблицы , поэтому её называют также и интерполяционной формулой Ньютона для интерполирования в начале таблицы. Отметим, что конечные разности, входящие в первую интерполяционную формулу Ньютона, расположены в верхней косой строке таблицы конечных разностей.

Погрешность первой интерполяционной формулы Ньютона записывается в виде

где – некоторая точка интервала, содержащего узлы интерполяции.

Вторая интерполяционная формула Ньютона. Пусть точка интерполирования лежит вблизи конечной точки таблицы . В этом случае для интерполирования применяется вторая интерполяционная формула Ньютона

Вторая интерполяционная формула Ньютона содержит конечные разности, расположенные в нижней косой строке таблицы конечных разностей.

Погрешность второй формулы

где – некоторая точка интервала, содержащего узлы интерполяции .

Интерполяционная формула Гаусса. Пусть точка интерполирования лежит в середине таблицы между узлами интерполяции и , т.е. . В этом случае для интерполирования применяется интерполяционная формула Гаусса

где ; – целая часть числа .

Погрешность интерполяционной формулы Гаусса имеет вид

где – некоторая точка интервала, содержащего узлы интерполирования.

Численное дифференцирование. Пусть функция задана таблицей своих значений . Требуется вычислить производную в некоторой точке .

Пусть для определенности точка находится в начале таблицы. Построим интерполяционный многочлен по первой формуле Ньютона

Производную приближённо можно вычислить следующим образом:

Если требуется найти производную в точке , лежащей в середине или в конце таблицы, то формулу для её вычисления получаем, исходя из формулы Гаусса или второй интерполяционной формулы Ньютона.

Обратное интерполирование. Задача обратного интерполирования заключается в определении по заданному значению функции , соответствующего значения . Если – монотонная непрерывная функция на интервале , причем , то функция в этом случае имеет обратную функцию.

Пусть задана функция :

Для многочлена Лагранжа нужно просто перевернуть таблицу:

Рассмотрим случай равноотстоящих узлов. Для определенности полагаем, что содержится между и (для 1-й формулы Ньютона). Этот метод называется методом последовательных приближений:

Используем метод итерации. Для этого необходимо уравнение привести к виду :

После приведения уравнения к виду, пригодному для метода итерации, в качестве начального приближения выбираем

Доказано, что при . В случае получения расходящегося процесса необходимо уменьшить h. Продолжая процесс итерации, получаем

Процесс итерации на практике продолжается до тех пор, пока не установятся цифры, соответствующие требуемой точности:

Для нахождения корня уравнения методом обратной интерполяции нужно рассмотреть функцию и составить таблицу ее значений, близких к нулю. При этом количество узлов выбирается в зависимости от требуемой точности корня. Выбираем интервал, на котором функция меняет знак, и решаем задачу обратного интерполирования, т.е. отыскиваем значение x, для котoрого y = 0.

Составить таблицу конечных разностей функций, заданных аналитически,
от начального значения х0 до конечного х7, приняв шаг равным h:

Составить таблицу конечных разностей функций, заданных аналитических
Составить таблицу конечных разностей функций, заданных аналитических, от начального значения x0 до.

Метод конечных разностей
Подскажите, пожалуйста, как правильно составить СЛАУ для данного метода. (ДУ 2ого порядка с.

Метод конечных разностей
Здравствуйте! Помогите, пожалуйста, мне необходимо реализовать метод конечных разностей для.

Решение уравнения теплопроводности методом конечных разностей
Всем доброго времени суток! Подскажите, пожалуйста, каким образом корректно задавать краевые и.

Решение двухточечных краевых задач методом конечных разностей
x2*y''-12y=0 ; x на отрезке , у(1)=1;у(2)=16. Точное решение у(х)=х4; Шаг h=0.2 Получил исходное.

решение уравнения параболического типа методом конечных разностей
Помогите дорешать лабораторную работу, не могу найти граничные условия (разностная схема может тоже.

метод сеток(конечных разностей). блок-схема
Помогите, пожалуйста!(( Скажите, как влияют х1 и х2 на блок-схему и вообще на решение?? в инете.

Метод конечных разностей для решения ДУЧП
Ребятки, здравствуйте! Всех с наступающим! :) Несколько времени тому назад мне под руку.

Под конечной разностью первого порядка функции f (x) принято понимать величину

где d – некоторая постоянная, которую часто, но не всегда, принимают равной 1. Разность второго порядка обозначается D2f и представляет собой разность разностей, т.е.

Продолжив этот процесс, мы получим разности более высоких порядков D3f (x), D4f (x), ј .

Данные выше определения можно также применить к членам любых последовательностей величин, например, к последовательности

3, 6, 11, 18, 27, 38, ј .

Первые разности равны

6 – 3, 11 – 6, 18 – 11, 27 – 18, 38 – 27, ј,

разности второго порядка постоянны и равны 2.

В общем виде такие последовательности можно записать как

где разности первого, второго и т.д. порядков определяются выражениями

а n может принимать любое допустимое для индекса значение.

В некоторых приложениях используются последовательности вида

Помимо уже названных выше приложений, исчисление конечных разностей используется в страховании, теории вероятностей и статистике. В последние годы с изобретением быстродействующих компьютеров конечные разности стали все более широко применяться при решении дифференциальных уравнений, обыкновенных и в частных производных, многие из которых ранее было невозможно решить другими математическими методами.

У истоков теории.

Хотя исследование свойств и использование конечных разностей приходится на современный период развития математики, Птолемей (ок. 150 н.э.) ввел в Альмагесте таблицу разностей первого порядка, чтобы облегчить расчеты в таблице длин хорд. Разности второго порядка использовал при вычислении своих таблиц логарифмов в 1624 Г.Бриггс. Теория интерполяции берет начало со знаменитой пятой леммы из 3-й книги Математических начал (1687) И.Ньютона, в которой впервые была приведена формула, носящая ныне его имя. Частный случай формулы Ньютона, открытый также независимо его современником Дж.Грегори (1638–1675), приведен ниже (см. формулу (7)). В общей формуле интерполяции Ньютона использовались разделенные разности, хотя этот термин, по-видимому, был введен О.де Морганом (1806–1871) в 1848. Первое применение исчисления конечных разностей к задачам теории вероятностей принято связывать с именами П.де Монтмора (1678–1719) и А.де Муавра (1667–1754).

Хотя Л.Эйлер (1707–1783) в своих работах по дифференциальному исчислению использовал предельные переходы в конечных разностях, основания современной теории конечных разностей были заложены в основном Ж.Лагранжем (1736–1813) и П.Лапласом (1749–1827). Первый из них ввел в исчисление конечных разностей символические методы, второй сделал конечные разности главным инструментом в своей Аналитической теории вероятностей (1812).

Под влиянием этих работ математики 19 в. принялись интенсивно разрабатывать предмет, и в 1860 Дж.Буль выпустил свой классический Трактат об исчислении конечных разностей. С тех пор это исчисление и круг его приложений существенно расширились. Одно из наиболее важных приложений конечные разности нашли в статистике. Особенно полезными они оказались в теории сериальной корреляции, в анализе случайных последовательностей и статистических временных рядов.

Интерполяция.

Чтобы понять, как конечные разности используются при интерполяции, рассмотрим следующую таблицу:

называется первой конечной разностью функции .

Конечные разности высших порядков

Пример. Построить конечные разности для функции:

Если - полином n-ой степени, то

Символ можно рассматривать как оператор, ставящий в соответствие функции функцию .

Основные свойства оператора :

Имеет место важная формула, которая может быть получена на основе свойств 1-3.

где - производная (непрерывная) на отрезке , .

Переходя к пределу и предполагая, что непрерывна, получаем

- формула для приближенного вычисления производных.

2) Таблица разностей.

Часто таблицы задаются для системы равноотстоящих точек

Конечные разности определяются соотношениями:

в силу свойства 1):

В общем виде можно записать:

где - число сочетаний из n элементов по m.

Например: ,

Для вычисления n-ой разности , нужно знать n+1 членов последовательности.

Конечные разности различных порядков удобно располагать в форме таблиц двух видов:

Горизонтальная таблица разностей. Диагональная таблица разностей.

Пример: Составить горизонтальную таблицу разностей функции

от начального значения , приняв шаг .

Решение: Полагая , , , находим , , .

Т.к. n=3 – степень полинома, то 3-и разности .

Заносим полученные значения в таблицу (горизонтальную).

0	-1	3	8	12
1	2	11	20	12
2	13	31	32	12
3	44	63	44	12
4	107	107	56	12

Исходные данные для заполнения таблицы отмечены ступенчатой ломаной.

Остальные клетки можно заполнить с помощью формул

Постановка задачи интерполирования.

На отрезке заданы n+1 точки , которые называются узлами интерполяции, и значение некоторой функции в этих точках

Требуется построить интерполирующую функцию F(x), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и , т.е.

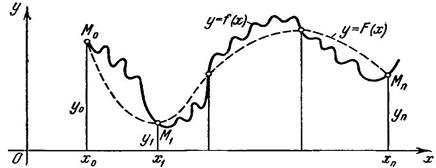
В общем случае, задача имеет бесчисленное множество решений.

Задача становится однозначной, если решение искать в заданном классе функций!

Будем искать полином степени не выше n и удовлетворяющий условию (2).

Полученную интерполяционную формулу используют для вычисления значений в точках (интервалах), отличных от узлов.

Если - имеет место задача интерполирования (интерполирование “в узком смысле”).

Пусть в каждом узле (i=1, 2,…, n) известны не только значения некоторой функция , но и значения ее производных , k =1, 2,…, – 1. В этом случае говорят, что узел имеет кратность . При интерполировании с кратными узлами строится интерполяционный многочлен Эрмита степени s-1 ( ), для которого выполняются условия

Чтобы доказать существование такого многочлена, построим его и получим оценку его погрешности.

Для простоты изложения построим многочлен (s=5) по двум кратным узлам. Пусть узел трехкратный ( ), а узел двукратный ( ). В этих узлах должны выполняться условия

Введем дополнительные вспомогательные узлы , , , , , . Эти пять узлов различны, можно построить единственный интерполяционный многочлен четвертого порядка. Запишем этот многочлен в виде интерполяционной формулы Ньютона с разделенными разностями

Для многочлена справедлива оценка

Используя формулу (10), покажем, что при существуют пределы коэффициентов многочлена . Заметим, что при узлы , и стремятся к , а и – к .

Вычислим пределы коэффициентов :

при , обозначим этот предел ;

Предел этого выражения при обозначим , он равен

Аналогично получается, что

Таким образом, при

Из формулы (11) при получается оценка для

Многочлен построен, проверим выполнение условий интерполяции:

первое условие проверяется подстановкой ;

Условия, заданные в точке , выполнены. Многочлен единствен и не изменится, если объявить первым узлом , а вторым , тогда

Легко убедиться, что и .

Аналогично, только более громоздко, строится интерполяционный многочлен с кратными узлами для произвольного значения s.

При построении таблицы разделенных разностей в случае кратных узлов сначала требуется заполнить строки, соответствующие кратным узлам. Остальные разделенные разности вычисляются обычным способом. Например, если имеет кратность 4, то этому узлу соответствуют четыре строки таблицы разделенных разностей, имеющие вид

Пример. Рассмотрим функцию

вторая производная которой в точке терпит разрыв первого рода. Сравним с построенным для неё интерполяционным многочленом с кратными узлами. Выберем три узла, два двукратных и , и один простой . Таблица разделенных разностей для этих узлов имеет вид

Интерполяционный многочлен имеет вид

Различие между функцией и соответствующим ей интерполяционным многочленом хорошо видно на рисунке

Постройте интерполяционный многочлен с кратными узлами для функции, у которой её значения и значения нескольких её производных заданы следующим образом

Постройте интерполяционный многочлен с кратными узлами для функции со следующими значениями самой функции и нескольких её производных

для равноотстоящих узлов

Пусть узлы , в которых заданы значения функции , равноотстоящие, т. е. для любого =0,1. n-1. В этом случае вместо разделенных разностей вводятся конечные разности.

Конечные разности и их свойства

Конечной разностью первого порядка называется выражение

Конечной разностью второго порядка называется

Конечной разностью k—ого порядка называется

Иногда конечная разность k—ого порядка обозначается .

С помощью метода математической индукции можно установить связь между разделенными и конечными разностями

Из этого равенства и формулы (10) получаем

Конечные разности, также как и разделенные, можно понимать как обобщение понятия производной в дискретном анализе.

Свойства конечных разностей определяются свойствами разделенных разностей:

Конечная разность — линейная операция

Если функция f(x) является полиномом n – ой степени, то конечные разности n – ого порядка постоянны, а (n+1) – ого порядка равны нулю.

Постройте таблицу конечных разностей для значений функции

Для какой функции составлена эта таблица?

Возьмите любой многочлен степени , вычислите его значения в (n+3) равноотстоящих узлах. Постройте таблицу конечных разностей, соответствующую вычисленным значениям.

Вычислите конечную разность , если функция задана своими значениями .

Постройте таблицу конечных разностей для функции в узлах , при условии, что её значение в известно с погрешностью ( ). Проследите, как распространяется эта погрешность в таблице конечных разностей.

Для равноотстоящих узлов оценку погрешности интерполяционного многочлена , построенного по узлам , можно записать в виде

Из этой оценки следует, что точность интерполяции в точке x (значение t фиксировано) можно увеличить, если

уменьшить h – шаг таблицы,

при шаге таблицы , увеличить n,

уменьшить значение константы C.

Может оказаться, что первый из указанных способов невозможен, например, таблица получена экспериментально, и её шаг нельзя изменить.

Второй из указанных способов накладывает жесткие требования на гладкость функции ( должна быть ограничена). Для экспериментально полученной функции (“зашумленной”) такие требования обычно не выполняются.

Константа C становится меньше, если выбрать ближайшие узлы к заданной точке x. Пусть задана таблица значений функции для большого числа равноотстоящих узлов ( ). Если интерполяционный многочлен строится для значения x, которое находится между узлами в начале таблицы, то ближайшими к x узлами являются , . Для конца таблицы ближайшие к x узлы — , .

Если же значение x находится среди узлов в середине таблицы, то в качестве нулевого узла интерполяции (ближайшего к x) выбирается значение , где индекс i равен целой части числа . Остальные узлы выбираются из значений , очевидно, значение k зависит от n. Если , то ближайшими к x являются узлы , если же , то — .

Рассмотрим интерполяционные формулы для всех вариантов расположения значения x.

Интерполяционные формулы Ньютона

для равноотстоящих узлов

Интерполяционная формула Ньютона для начала таблицы (интерполяция вперед)

Выберем узлы и запишем интерполяционную формулу с разделенными разностями

Сделаем замену , тогда , а выражения для разделенных разностей примет вид

Теперь интерполяционный многочлен Ньютона для точки x, расположенной в начале таблицы, запишется в виде

Интерполяционная формула Ньютона для конца таблицы (интерполяция назад)

Выберем узлы и запишем интерполяционную формулу с разделенными разностями

Здесь удобна замена , тогда , и для разделенных разностей получим выражения

Теперь интерполяционный многочлен Ньютона для конца таблицы принимает вид

Интерполяционные формулы Гаусса

Интерполяционные многочлены Гаусса строятся для значений x, находящихся в середине таблицы.

Первая формула Гаусса

Первая формула Гаусса получается, если в качестве узлов интерполяции выбраны , при n=2m+1 (последний узел отбрасывается, если n=2m).

Формула Ньютона с разделенными разностями для таких узлов имеет вид

Здесь имеются разделенные разности двух типов

Сделаем замену , тогда , первая формула Гаусса примет вид

Вторая формула Гаусса

Вторая формула строится также как первая, только выбраны узлы .

Для таких узлов формула Ньютона с разделенными разностями имеет вид

Сделаем ту же замену , и вторая формула Гаусса примет вид

Формулы Гаусса используют конечные разности, лежащие вблизи горизонтали, проходящей через . Эти разности называются центральными.

Отметим еще раз, что различные интерполяционные многочлены, построенные для одного набора узлов, являются различными формами записи одного и того же многочлена.

Построим таблицу конечных разностей, и отметим на ней, какие конечные разности используются в различных интерполяционных формулах

Оптимальный выбор узлов интерполяции

Если значения функции получаются с помощью трудоемкого расчета, то можно поставить вопрос о вычислении значений в таких узлах , чтобы в оценке погрешности интерполяции

для многочлена выполнялось условие

где произвольный многочлен степени с коэффициентом при старшей степени .

Такие многочлены существуют, они с точностью до множителя совпадают с многочленами Чебышева и называются наименее уклоняющимися от нуля.

Многочлены Чебышева нулевой и первой степени имеют вид

а многочлены n — ой степени выписываются с помощью рекуррентной формулы

Легко показать (с помощью математической индукции), что — четная функция, а — нечетная. Из рекуррентной формулы следует, что коэффициент при старшей степени , n>1 равен .

У многочлена Чебышева существует n различных вещественных корней, которые находятся на отрезке . Чтобы найти эти корни, запишем на в виде

Для корней такого многочлена получаются формулы

Экстремумы многочлена Чебышева достигаются в точках , , , причем

Сравним значения модулей многочленов и произвольного многочлена . У обоих этих многочленов коэффициенты при старших степенях равны единице.

Лемма. Если — произвольный многочлен степени n с коэффициентом при старшей степени равным единице, то

Доказательство. Предположим противное, пусть . Степень многочлена не выше (n-1) (старшие степени уничтожаются). В силу предположения, он не равен нулю тождественно. Если для любого , то знак разности в точках экстремума многочлена Чебышева

совпадает со знаком .

Это означает, что многочлен меняет знак на отрезке в (n+1)–ой точке, т.е. имеет n корней. Отличный от нуля многочлен степени не более (n-1) не может иметь n корней. Получили противоречие, лемма доказана.

Заметим, что многочлены

образуют на отрезке ортонормированную с весом систему многочленов, т.е.

Сделаем замену , тогда, если , то . Корням , полинома на отрезке , отвечают точки на отрезке . Если эти точки взять в качестве узлов интерполяции, то

Это означает, что

Для выбранных узлов интерполяции получается оценка

и её нельзя улучшить за счет выбора любых других узлов.

З
амечание . На опасность появления большой погрешности интерполяции обратил внимание в 1901г. Рунге. На отрезке рассматривалась аналитическая функция (на рисунке изображен её график).

Если при построении интерполяционного многочлена для этой функции, выбрать равноотстоящие узлы, например, для n=6, то при последовательность не сходится к для значений .

Если же в качестве узлов выбирать корни полинома Чебышева, то для любого значения .

Есть теорема Фабера: если непрерывно дифференцируема (одной непрерывности мало), то интерполяционные многочлены , построенные на отрезке по узлам, совпадающим с корнями многочлена Чебышева, сходятся к при .

Сколько интерполяционных многочленов степени n-1 можно построить по заданным n узлам?

Сформулируйте постановку задачи интерполяции. Что такое экстраполяция?

Сформулируйте постановку задачи интерполяции с кратными узлами.

Как отличаются друг от друга различные интерполяционные многочлены (Лагранжа, Ньютона, и т.п.), построенные по одному и тому же набору узлов?

Как оценивается погрешность интерполяционного полинома? Как её можно уменьшить?

Как оптимальным образом выбрать узлы интерполяции?

Перечислите свойства разделенных разностей.

Перечислите свойства конечных разностей.

Для каких функций погрешность интерполяции равна нулю?

Пусть задана большая таблица значений функции. Как расположение значения х влияет на выбор интерполяционной формулы? Как наилучшим образом выбрать степень интерполяционного многочлена?

Пусть , постройте интерполяционный многочлен , совпадающий с функцией в точках x=0, x=1, x=2. Оцените на отрезке . Сравните эту оценку с фактической погрешностью в точке x=1/2 (или x=3/2).

Пусть , . Определите шаг h таблицы значений , чтобы линейная интерполяция (многочлен ) обеспечивала точность .

Пусть на отрезке заданы значения функции в узлах , ( ). Определите, при каком значении числа n для интерполяционного многочлена будет выполняться оценка для любого .

На сетке , , заданы значения , где – многочлен Чебышева. Вычислите значение .

Читайте также: