Как сделать семиугольник

Обновлено: 08.07.2024

В геометрии , A - угольник представляет собой семь-сторонний многоугольник или 7-угольник.

Содержание

Регулярно угольник , в котором все стороны и все углы равны, имеет внутренние углы из его / 7 радиана (128 4 / ₇ градусов ). Его символ Шлефли - .

Площадь ( A ) правильного семиугольника с длиной стороны a определяется как:

Точное алгебраическое выражение , начинающееся с кубического многочлена 8 x 3 + 4 x 2 - 4 x - 1 (один из корней которого равен ) [1] , дается в комплексных числах следующим образом: потому что ⁡ 2 π 7 >>

в котором мнимые части компенсируют друг друга, оставляя выражение с действительным знаком. Это выражение нельзя переписать алгебраически без сложных компонент, так как указанная кубическая функция есть casus unducibilis .

Площадь правильного семиугольника, вписанного в круг радиуса R, равна площади самого круга, поэтому правильный семиугольник заполняет приблизительно 0,8710 его описанной окружности . 7 R 2 2 sin ⁡ 2 π 7 , >>\sin >,> π R 2 ; <\displaystyle \pi R^;>

Поскольку 7 - простое число Пьерпона, но не простое число Ферма , правильный семиугольник нельзя построить с помощью циркуля и линейки, но можно построить с помощью отмеченной линейки и компаса. Это самый маленький правильный многоугольник с этим свойством. Такой тип конструкции называется конструкцией neusis . Его также можно построить с помощью циркуля, линейки и трисектора угла. Невозможность построения линейки и циркуля следует из наблюдения, которое является нулем неприводимой кубики x 3 + x 2 - 2 x - 1. 2 cos ⁡ 2 π 7 ≈ 1.247 >\approx 1.247>> . Следовательно, этот многочлен является минимальным многочленом из 2cos ( 2π / ₇ ), в то время как степень минимального полинома для конструктивного числа должна быть степенью 2.

Гептагон с заданной длиной стороны :
Анимация из конструкции neusis с отмеченной линейкой, по словам Дэвида Джонсона Лейска ( Crockett Johnson ) [2], пауза в конце 30 с.

Джерард 'т Хофт показывает правильный семиугольник, состоящий всего из 15 полосок Meccano с размером стержней 8 и 11. [3]

Конструкция состоит из двух равнобедренных треугольников, на которых закреплены остальные стержни. Сторона правильного семиугольника a , сторона более короткого равнобедренного треугольника e и сторона более длинного равнобедренного треугольника d удовлетворяют условиям

Формула получена из формулы Гептагонального треугольника :

Небольшие возможные конструкции семиугольника:

Семиугольник	а	d	е
1	3	4	1
2	8	11	6
3	33	46	29
4	40	53	6
5	55	74	27

Самый маленький семиугольник конструктора 1:

Примерное значение для практического использования с погрешностью около 0,2% показано на чертеже. Его приписывают Альбрехту Дюреру . [4] Пусть A лежит на окружности описанной окружности. Нарисуйте дугу BOC . Затем дает приближение для края семиугольника. B D = 1 2 B C BC>>

Это приближение используется для стороны семиугольника, вписанного в единичный круг, в то время как точное значение . 3 2 ≈ 0.86603 > \over 2>\approx 0.86603> 2 sin ⁡ π 7 ≈ 0.86777 \approx 0.86777>

Пример для иллюстрации ошибки:
при радиусе описанной окружности r = 1 м абсолютная погрешность 1-й стороны будет приблизительно -1,7 мм.

Построение аппроксимации меккано может быть выполнено с одиннадцатью стержнями размером 20, 36 и 45. Эти значения оставляют ошибку около 0,1%.

Симметрии правильного семиугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. В центре даны приказы гирации. [5]

Регулярно угольник относится к D 7h точечной группы ( Шенфлиса обозначение ), порядка 28. Элементы симметрии: 7-кратное правильное вращение оси С ₇ , 7-кратное неправильное вращение оси а, S ₇ , 7 вертикальные плоскости зеркала, σ _v , 7 2-кратные оси вращения C ₂ в плоскости семиугольника и горизонтальная зеркальная плоскость σ _h также в плоскости семиугольника. [6]

Сторона правильного семиугольника a , более короткая диагональ b и более длинная диагональ c , при a [7] : Лемма 1

Таким образом, - b / c , c / a и a / b все удовлетворяют кубическому уравнению. Однако для решений этого уравнения не существует никаких алгебраических выражений с чисто действительными членами, потому что это пример casus unducibilis . t 3 − 2 t 2 − t + 1 = 0. -2t^-t+1=0.>

Приблизительная длина диагоналей относительно стороны правильного семиугольника определяется выражением

b ≈ 1.80193 ⋅ a , c ≈ 2.24698 ⋅ a .

У нас также есть [8]

У семиугольного треугольника есть вершины, совпадающие с первой, второй и четвертой вершинами правильного семиугольника (от произвольной начальной вершины), и углы, и, таким образом, его стороны совпадают с одной стороной и двумя конкретными диагоналями правильного семиугольника. [7] π / 7 , 2 π / 7 , 4 π / 7.

Два типа звездных семиугольников ( гептаграммы ) могут быть построены из правильных семиугольников, помеченных символами Шлефли и , причем делитель представляет собой интервал соединения.

Синие, и зеленые звездные семиугольники внутри красного семиугольника.

Задача о геометрии поверхности семиугольника, разделенного на треугольники, на глиняной табличке школы писцов; Сузы , первая половина II тыс. До н. Э.

Соединенное Королевство в настоящее время (2020) имеет две семиугольной монеты , в 50p и 20p штук, а Барбадос доллар также семиугольный. В монете номиналом 20 евроцентов углубления размещены аналогично. Строго говоря, форма монет представляет собой семиугольник Рело , криволинейный семиугольник, который делает их кривыми постоянной ширины : стороны изогнуты наружу, так что монета будет плавно катиться при вставке в торговый автомат . Ботсвана пуламонеты достоинством 2 Пула, 1 Пула, 50 Фив и 5 Фив также имеют форму семиугольника равносторонней кривой. Монеты в форме семиугольника Рило также находятся в обращении на Маврикии, ОАЭ, Танзании, Самоа, Папуа-Новой Гвинее, Сан-Томе и Принсипи, Гаити, Ямайке, Либерии, Гане, Гамбии, Иордании, Джерси, Гернси, острове Мэн, Гибралтар, Гайана, Соломоновы острова, Фолклендские острова и остров Святой Елены. Монета Замбии в 1000 квача - это настоящий семиугольник.

На бразильской 25-центовой монете нанесен семиугольник на диске. В некоторых старых версиях герба Грузии , в том числе в советские времена , в качестве элемента использовалась гептаграмма .

В архитектуре семиугольные планы этажей встречаются очень редко. Замечательный пример - мавзолей принца Эрнста в Штадтхагене , Германия .

Многие полицейские значки в США имеют контур гептаграммы .

За исключением семиугольной призмы и семиугольной антипризмы , ни один выпуклый многогранник, полностью состоящий из правильных многоугольников, не содержит семиугольника в качестве грани.

Обычные семиугольники могут перекрывать гиперболическую плоскость , как показано в этой проекции модели диска Пуанкаре :

Полный граф K ₇ часто рисуется как правильный семиугольник со всеми 21 ребром, соединенным. Этот граф также представляет собой ортогональную проекцию 7 вершин и 21 ребра 6-симплекса . Регулярный перекос полигон по периметру называется Petrie полигон .

Окружность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки О. Эта точка называется центром окружности(см.рис.3). Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом (R). Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда – отрезок, соединяющий любые две точки окружности. Хорда, проходящая через центр окружности, называется диаметром. Диаметр вдвое больше радиуса: он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды. Любые две не совпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром. Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. Практическое построение окружности производится с помощью циркуля.

Окружность называется описанной вокруг многоугольника в том случае, если все вершины многоугольника лежат на этой окружности (см.рис.4 ).

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности, а многоугольник называется описанным около этой окружности (см.рис.5 ).

Центральный угол - это угол, вершина которого находится в центре окружности (см.рис.6).

Коробовые кривые.

2.1.2.1 Овалы (См. Приложение Б1).

2.1.2.2 Овоиды (См. Приложение Б2).

2.1.3 Своды(См. Приложение Б3).

2.1.4 Завитки(См. Приложение Б4).

2.1.5 Архитектурные обломы(См. Приложение Б5).

Лекальные кривые

Существует большое количество лекальных кривых. Для исследования взяты кривые сечения конуса, циклические кривыеи линия изогнутой гибкой рейки.

Точное построение кривых сечений конуса выполняется с помощью циркуля (см.табл.1).

Произвольные кривые сечения конуса можно выполнить и без помощи циркуля. Например, зная определение эллипса, можно сделать простейший прибор, вычерчивающий эллипс (см.рис.7). Для этого надо два гвоздика вонзить в чертёжную доску, надеть на них кольцо из нитки,а карандаш двигать по бумаге так, чтобы он всё время натягивал нитку. Тогда кончик грифеля будет рисовать на бумаге эллипс.

Рис.7

Кривые сечения конуса

2.2.1.1 Эллипс		Параметры АВ и СD (задаются) – большая и малая оси, взаимно перпендикулярны, делятся пополам точкой О – центром эллипса. Положение фокусов F₁ и F₂ на большой оси определяется засечками дуги радиусом ОА=АВ:2, проведённой из точки С или D. Эллипс обладает таким свойством: сумма расстояний от каждой точки М, N… до фокусов постоянна и равна большой оси эллипса: F₁М и F₂М = F₁N + F₂N. Эта формула – математический закон, которому подчиняются все точки эллипса.
2.2.1.2 Пара-бола		Х – ось параболы (линия симметрии); F – фокус; l – (директриса) прямая линия, перпендикулярная к оси Х; P=OF – параметр параболы (задаётся); А – вершина (точка пересечения оси Х с ветвью параболы), ОА=Р:2=ОF:2.
2.2.1.3 Гипер-бола		О – центр; 2а – параметр (задаётся); X и Y – две взаимно перпендикулярные оси симметрии, Х – главная (действительная) ось; Y – малая (мнимая) ось; А и В – вершины гиперболы; F₁ и F₂ - фокусы гиперболы; Асимптоты – две прямые, к которым гипербола стремится, но никогда с ними не пересекается.

После кривых сечений конуса можно обратиться к циклическим кривым (см.рис.8, 9,10).

а) б)

Теперь на велосипеде с помеченной точкой проедем по яме, представляющей в разрезе дугу окружности – точка опишет гипоциклоиду.

Гипоциклоида – плоская кривая, описываемая точкой производящей окружности, которая без скольжения катится по направляющей окружности, при этом направляющая и производящая окружности имеют внутреннее касание (см.рис12).

Рис.12 Рис.13

И ещё раз проедем, только теперь по небольшому холмику, представляющей в разрезе тоже дугу окружности – точка опишет эпициклоиду.

Эпициклоида – плоская кривая, описываемая точкой производящей окружности, которая без скольжения катится по направляющей окружности, при этом производящая и направляющая окружности имеют внешнее касание (см.рис.13).

При точном построении находятся точки, по которым и обводятся циклические кривые. Основной инструмент здесь лекало, они поэтому так и называются- лекальные кривые, но циркуль здесь главный помощник.

Давно математики пытались решить такую задачу: какой формы должен быть гладкий жёлоб, соединяющий две точки А и В (А выше, чем В), чтобы гладкий металлический шарик скатился по этому желобу из точки А в точку В под действием своего веса за кратчайшее время? Можно подумать, что жёлоб должен быть прямолинейным. Но это не так. Может быть, следует выгнуть по дуге окружности, как думал великий итальянский физик, астроном и математик Галилео Галилей, живший на рубеже XVI – XVII вв.? Нет, Галилей ошибался. Только в 1696 г. швейцарский математик Иоганн Бернулли установил, что желоб должен быть выгнут по циклоиде, опрокинутой вниз (см.рис.14, 15).

Рис.14

Рис.15

Для того, чтобы подтвердить это, был проведён эксперимент. Вместо жёлоба была взята полиэтиленовая труба (она имеет свойство сгибаться). Для чистоты эксперимента, чтобы согнуть трубу по циклоиде, на четырёх листах ватмана была построена половина циклоиды с исходным диаметром 95 см.

Сначала засекалось время скатывания шарика по кривой линии (см.рис.16), потом – по циклоиде (см.рис.17) и последнее – по прямой (см.рис.18).

Рис.16 Рис.17 Рис.18

В результате эксперимента выявлено время движения шарика по разным видам трассы (см.табл.2).

Таблица 2 Время движения шарика по трассе

Линия прохождения трассы	Длина трассы L, см	Время прохождения трассы t, с	Место
Кривая	402,0	1,09	II
Циклоида	386,6	0,95	I
Прямая	298,3	1,27	III

Результат эксперимента подтвердил, что скорость прохождения по трассе минимальная в том случае, когда трасса выполнена в виде циклоиды, перевёрнутой вниз: 0,95 секунды при условии, что длина трассы по циклоиде гораздо длиннее, чем по прямой и чуть меньше, чем по кривой. Это должно учитываться при сооружении спортивных трасс.

И ещё одна, последняя из исследуемых лекальных кривых, - линя изогнутой гибкой рейки. На рис.19 показано построение формы купола. Кривая его очерка представляет собой сочетание двух кривых, отображающих различные условия работы материала (линия О-2 – растяжение, линия 2-1-3 – сжатие). Последний участок выражает линию равного сопротивления – очертание изогнутой гибкой рейки.

Рассмотрим графическое построение линии изогнутой рейки (см.рис.20).На прямой линии выбирают точку О – полюс и вершину А кривой. Вычерчивают окружность, центр которой лежит на прямой ОА. На отрезке АВ проводят ряд прямых, перпендикулярных ему. Из точки В проводят лучи к точкам пересечения параллельных прямых с окружностью (точки 1₀, 2₀, 3₀, 4₀), а из точки О проводят лучи, параллельные соответствующим лучам первого пучка, также до пересечения с параллельными прямыми. Получим искомые точки 1, 2, 3, 4.

Величина параметраa относительно диаметра окружности определяет степень изгиба, если он уменьшается – изгиб увеличивается. Для того, чтобы подтвердить это, будем менять параметр a (см. рис.21-23). Действительно, исследование подтверждает, что при увеличении параметра aизгиб уменьшается (см. рис.21), а при уменьшении – увеличивается (рис.23).

Рис.21 Рис.22 Рис.23

И ещё одна закономерность выявлена при исследования линии изогнутой гибкой рейки: если поменять параметрa и радиус (или диаметр) исходной окружности в одинаковой пропорции (принят к=1,5 на чертеже), то изгиб получается примерно одинаковым (см. рис.24).

Рис.24

Заключение

На первом этапе, вгеометрических построениях,выявлено, что при построении параллельных прямых можно в одном случае построить параллелограмм, во втором – ромб, в третьем – трапецию, а в четвёртом случае – соответственные углы (см.п.1.1.3.2). Даны примеры применения геометрических построений в геометрии, черчении и технике.

На втором этапеисследованы циркульные кривые и построениес их помощью геометрических тел и развёрток. Исследовано применение циркульных кривых в покрытиях зданий, в арках, колоннах, в архитектуре Кемеровской области (см. Приложение Б8 - Б11).

На третьем этапе исследовательской работы для исследования лекальных кривых выбраны кривые сечения конуса, циклические кривые и линия изогнутой гибкой рейки.

Особый интерес из кривых сечений конуса вызвала парабола. Проведено исследование дальности полёта шарика в зависимости от угла наклона дула детского пистолета (см. Приложение В2). В результате исследования выявлено, что дальность полёта (по параболе) шарика максимальная, если угол наклона дула составляет 45 0 . Это свойство можно использовать на уроках физкультуры при метании спортивных снарядов: мяча, гранаты, ядра, копья.

При исследовании циклических кривых был проведён эксперимент, который подтвердил вывод Бернулли о том, что кратчайшее время скатывания шарика с верхней точки А в нижнюю точку В по наклонной под действием собственного веса должно быть по циклоиде, опрокинутой вниз.

Поставленная цель работы: выявление построений с помощью циркуля и применения этих построений – достигнута.

Гипотеза доказана: Если уметь чертить с помощью циркуля, можно таким образом решать различные задачи, строить чертежи, научиться видеть в окружающем нас мире удивительный мир геометрических фигур.

Правильный семиугольник

CherkasovMY - бан на две недели за агрессивное невежество и частичное возобновление удаленной ранее темы. Можно также заметить, что это очередная "попытка рекламы лженауки" (хотя цитируемый учебник/сайт по техническому черчению сам по себе вполне корректен, вы усмотрели в нем именно лженаучное утверждение).

На указанной странице нигде не говорится о том, что построенный семиугольник только приблизительно правилен. Нельзя ли указать то место, где это сказано?

Тогда откуда утверждение, что исходный текст "вполне корректен"?

Построения циркулем и линейкой излагаются как на математике, так и на черчении. Ряд чертёжных построений точен математически. Это - нет. Где это оговорено?

Тогда можно так же заявить, что и построенный шестиугольник неправилен.

Ваш вывод субъективен.

Почему? Общий уровень строгости/корректности/etc. — это инфимум уровней частей, это не даёт нам верхней границы.

Потому что в тексте, повторяю , ничего не сказано о различиях построений шестиугольника и семиугольника.
А то, что приведённый рецепт построения шестиугольника точен, каждый знает со школы.

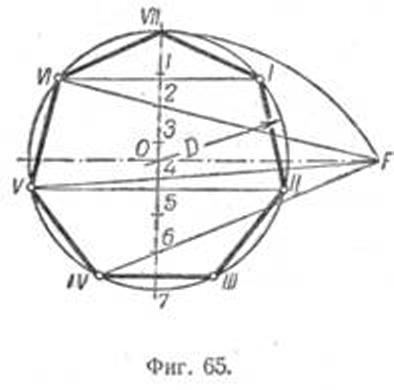
Пусть радиус окружности равен 1. Точное значение квадрата стороны вписанного 7-угольника: 0.7530. Значение квадрата стороны VI-VII вычисленное с помощью приведенного построения равно: 0.7554. Видно, что построение имеет точность около 0.5%.

Я не понимаю, какая разница, сказано там, что построение приближённое, или нет.
Есть теорема о том, что правильный -угольник можно построить циркулем и линейкой тогда и только тогда, когда число сторон имеет вид , где и — неотрицательные целые числа, а — попарно различные простые числа Ферма.
Числа Ферма имеют вид +1$" />
, где — неотрицательное целое число. Простых чисел Ферма в настоящее время известно штук: . Число не имеет указанного вида, поэтому -угольник нельзя построить циркулем и линейкой, хотя приближённые построения имеются и могут иметь сколь угодно малую погрешность.

Но это чисто математический результат, который предполагает, что построения циркулем и линейкой являются совершенно точными. Построения на реальной бумаге с помощью реальной линейки и реального циркуля всегда приближённые. Речь в данном случае идёт о техническом черчении, где разницы между абсолютно точными и "достаточно" точными построениями нет. Я окончил школу в 1967 году и до сих пор помню, что вместо эллипса рисуют овал, составленный из четырёх дуг окружностей. Поэтому я не вижу, зачем в тексте, относящемся к техническому черчению, специально акцентировать внимание на том, что некоторые построения "точные", а некоторые — приближённые. "Точные" построения на самом деле тоже приближённые. В этом легко убедиться, воспроизведя "точное" построение пятиугольника (рисунок 63): отложив по окружности раз сторону 1-2, мы не вернёмся точно в точку 1, хотя математически это построение точное.

Что касается спора о точности построения на рисунке 65, то ведь надо просто вычислить стороны или углы построенного семиугольника и сравнить их между собой. Об этом уже написал worm2 , а пока я сочинял этот текст, вычисления проделал mihiv .

Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой.

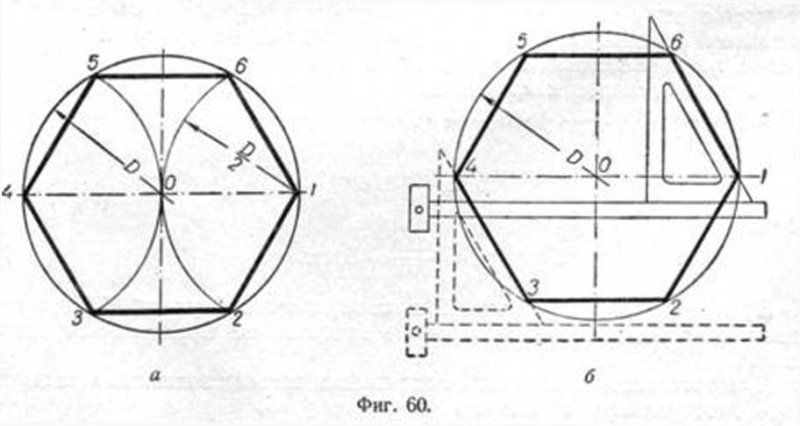
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.

Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0 — 1 — 2 равен 30°, то для нахождения стороны 1 — 2 достаточно построить по точке 1 и стороне 0 — 1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1 — 2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2 — 3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

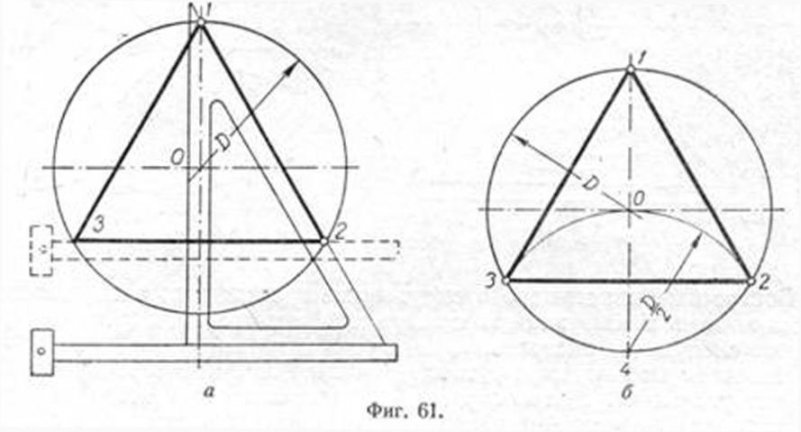
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника намечаем на диаметре вершину точку 1 и проводим диаметральную линию 1 — 4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

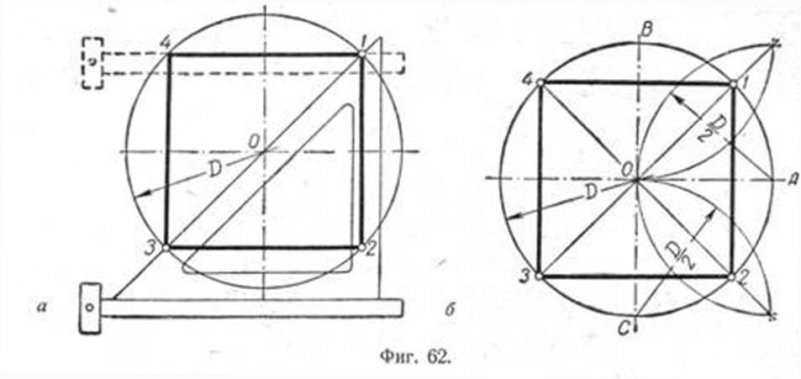
Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4 — 1 и 3 —2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1 — 2 и 4 — 3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра. Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Чтобы вписать в окружность правильный пятиугольник, производим следующие построения. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

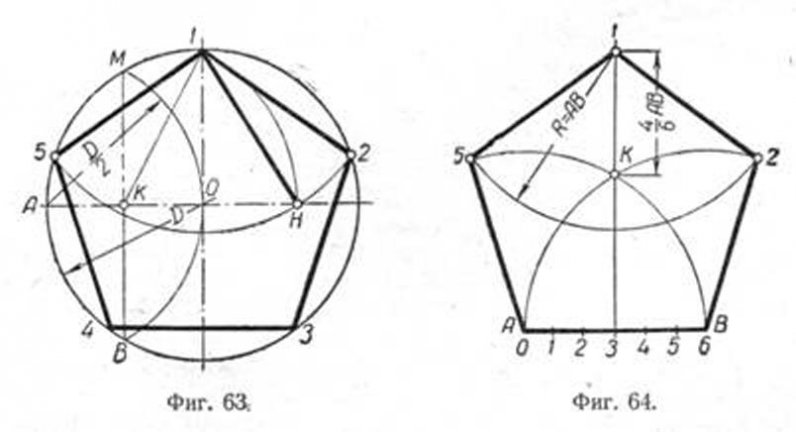
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую. Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB. Получим точку 1 —вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

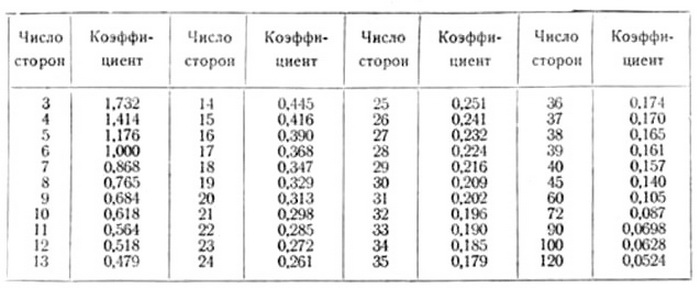
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй — коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Читайте также: