Как сделать разложение вектора по базису

Обновлено: 05.07.2024

Данный онлайн калькулятор позволяет по заданному базису разложить произвольный вектор. Для этого достаточно ввести координаты векторов базиса и искомого вектора и калькулятор выдаст ответ с подробным решением.

Разложение вектора по базису онлайн.

Размерность пространства векторов:

Введите значения векторов:

Введите значение вектора который нужно разложить по базису:

Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.

Разложение вектора по базису онлайн

Разложение по базису

Линейной комбинацией векторов

Чтобы разложить, вектор

при этом коэффициенты

Все онлайн калькуляторы

• Правила ввода функций и констант
• Инженерный калькулятор
• Математический анализ
  • Вычислить неопределенный интеграл
  • Вычислить определенный интеграл
  • Вычислить двойной интеграл
  • Вычислить производную
  • Вычислить предел функции
  • Вычислить сумму ряда
  • Найти определитель матрицы
  • Найти обратную матрицу
  • Решение дифференциальных уравнений
  • Решение квадратных уравнений
  • Решение системы линейных уравнений (метод подстановки)
  • Решение системы линейных уравнений (метод Гаусса)
  • Решение системы линейных уравнений (метод Крамера)
  • Решение системы линейных уравнений (матричный метод)
  • Уравнение прямой по двум точкам
  • Уравнение плоскости по трем точкам
  • Расстояние между точкой и прямой
  • Расстояние между точкой и плоскостью
  • Скалярное произведение векторов
  • Векторное произведение векторов
  • Смешанное произведение векторов
  • Проверить, образуют ли вектора базис
  • Разложить вектор по базису
  • Построить график онлайн

  Работы на заказ

  Объявление

  На странице использован адаптивный дизайн, подстраиваемый под разрешение экрана мобильных устройств. Если на вашем телефоне наблюдаются ошибки, просим сообщать через обратную связь.

  
  
  
  
  
  

  Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

  Упорядоченная тройка некомпланарных векторов $e_1, e_2, e_3$ называется базисом в пространстве всех геометрических векторов. Всякий геометрический вектор $a$ может быть представлен единственным образом в виде $$a=X_1e_1+X_2e_2+X_3e_3.\qquad\qquad\qquad\qquad\qquad (1)$$ Числа $X_1, X_2, X_3$ называются координатами вектора в базисе $B=\.$ Запись (1) называют разложением вектора $a$ по базису $B.$

  Аналогично, упорядоченная пара неколлинеарных векторов $e_1, e_2$ называется базисом $B=(e_1, e_2)$ в множестве геометрических векторов, компланарных некоторой плоскости.

  Наконец, всякий ненулевой вектор $e$ образует базис $B=(e)$ в множестве геометрических векторов, коллинеарных некоторому направлению.

  Если вектор $a$ есть линейная комбинация векторов $a_1, a_2, . a_n$ с коэффициентами $\lambda_1, \lambda_2, . \lambda_n$, то есть $$a=\sum\limits_^n \lambda_ka_k$$ то каждая координата $X_i(a)$ вектора $a$ равна сумме произведений коэффициентов $\lambda_1,\lambda_2. \lambda_n$ на одноименные координаты векторов $a_1, a_2, . a_n: $ $$X_i(a)=\sum\limits_^n\lambda_k X_i(a_k),\qquad (i=1, 2, 3.)$$

  Базис $B=(e_1, e_2, e_3)$ называется прямоугольным, если векторы $e_1, e_2$ и $e_3$ попрано перпендикулярны и имеют единичную длину. В этом случае приняты обозначения $$e_1=i;\,\, e_2-j;\,\, e_3=k.$$

  Примеры.

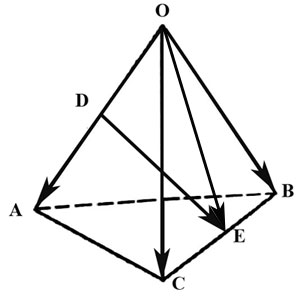
  2.26. Задан тетраэдр $OABC.$ В базисе из ребер $\overline, \overline$ и $\overline$ найти координаты:

  а) вектора $\overline,$ где $D$ и $E$ середины ребер $OA$ и $BC.$

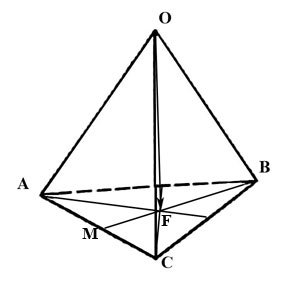
  б) вектора $\overline,$ где $F-$ точка пересечения медиан основания $ABC.$

  Решение.

  а)

  
  

  Выразим вектор $\overline$ через вектора $\overline, \overline, \overline:$

  Из треугольника $ODE$ имеем $\overline=\overline+\overline.\qquad\qquad\qquad (1)$

  вектор $\overline$ найдем из треугольника $OBE:$

  здесь $\overline=\frac\overline,$ а вектор $\overline$ находим из треугольника $OBC:$

  Таким образом, из (2) получаем $\overline=\overline+\frac(\overline-\overline).$

  Наконец из (1) имеем $$\overline=\overline+\overline=-\frac\overline+\overline+\frac(\overline-\overline)=$$ $$=-\frac\overline+\frac\overline+\frac\overline.$$

  Таким образом, координаты вектора $\overline$ в базисе из ребер $\overline, \overline, \overline:$ $\left(-\frac,\frac,\frac\right).$

  Ответ: $\left(-\frac; \frac; \frac\right).$

  б)

  
  

  Выразим вектор $\overline$ через вектора $\overline, \overline, \overline:$

  Из треугольника $OFB$ имеем $\overline=\overline+\overline.\qquad\qquad\qquad (1)$

  вектор $\overline$ найдем из треугольника $BMC:$

  здесь $\overline=\frac\overline,$ а вектор $\overline$ находим из треугольника $OCA:$

  Таким образом, из (2) получаем $$\overline=\overline+\overline=\overline-\overline+\frac\overline=$$ $$=\overline-\overline+\frac(-\overline+\overline).$$

  Наконец из (1) имеем $$\overline=\overline+\overline=\overline+\frac\overline=$$ $$=\overline+\frac\left(\overline-\overline+\frac(-\overline+\overline)\right)=$$ $$=\overline+\frac\overline-\frac\overline+\frac(-\overline+\overline)=\frac\overline+\frac\overline+\frac\overline.$$

  Таким образом, координаты вектора $\overline$ в базисе из ребер $\overline, \overline, \overline:$ $\left(\frac; \frac; \frac\right).$

  Ответ: $\left(\frac; \frac; \frac\right).$

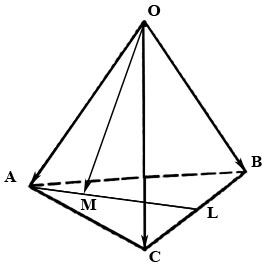
  2.27. В тетраэдре $OABC$ медиана $AL$ грани $ABC$ делится точкой $M$ в отношении $|\overline|:|\overline|=3:7.$ Найти координаты вектора $\overline$ в базисе из ребер $\overline, \overline, \overline.$

  Решение.

  
  

  Вектор $\overline$ найдем из треугольника $AOM:$ $$\overline=\overline+\overline.\qquad\qquad\qquad (1)$$

  Из условия $|\overline|:|\overline|=3:7$ имеем $\overline=\frac\overline.$ Из треугольника $ABL$ находим $\overline=\overline+\overline=\overline+\frac\overline.$

  Далее, из треугольников $AOB$ и $BOC$ получаем

  Отсюда и из (1) получаем $$\overline=\overline+\overline=\overline+\frac\overline+\frac\overline+\frac\overline=$$ $$=\frac\overline-\frac\overline+\frac\overline.$$

  Ответ: $\left(\frac; \frac;\frac\right).$

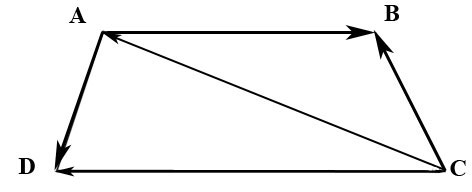
  2.29. В трапеции $ABCD$ известно отношение длин оснований $|\overline|/|\overline|=\lambda$ Найти координаты вектора $\overline$ в базисе из векторов $\overline$ и $\overline.$

  Решение.

  
  

  Вектор $\overline$ можно найти из треугольника $ABC:$ $\overline=\overline+\overline.$

  $\overline$ находим из треугольника $ACD:$ $\overline=\overline+\overline=\overline-\overline.$

  Из условия $|\overline|/|\overline|=\lambda$ находим вектор $\overline:$ $\overline=-\overline/\lambda.$

  Таким образом, $\overline=-\overline/\lambda-\overline;$

  Ответ: $\left(1-\frac<\lambda>; -1\right).$

  2.36. Заданы векторы $e(-1, 1, 1/2)$ и $a(2, -2, -1).$ Убедиться, что они коллинеарны и найти разложение вектора $a$ по базису $B(e). $

  Решение.

  Векторы коллинеарны, если их направления совпадают или противоположны, т.е. тогда и только тогда когда их координаты пропорциональны. Проверим: $$\frac=\frac=\frac=-\frac,$$ то есть векторы $e$ и $a$ коллинеарны.

  Найдем разложение вектора $a$ по базису $B(e),$ то есть найдем такое число $\lambda$ что $a=\lambda e:$

  Ответ: $a=-2e.$

  Домашнее задание.

  2.28. Вне плоскости параллелограмма $ABCD$ взята точка $O.$ В базисе из векторов $\overline, \overline$ и $\overline$ найти координаты:

  а) вектора $\overline$ , где $M$ точка пересечения диагоналей параллелограмма;

  б) вектора $\overline,$ где $K$- середина стороны $AD.$

  Ответ: а) $(1/2; 0; 1/2);$ б) $(1, -1/2, 1/2).$

  2.31. В треугольнике $ABC$ $\overline=\alpha\overline; \overline=\beta\overline;$ $\overline=\gamma\overline.$ Пусть $P, Q$ и $R -$ точки пересечения прямых $BF$ и $CK;$ $CK$ и $AM;$ $AM$ и $BF$ соответственно. В базисе из векторов $\overline$ и $\overline$ найти координаты векторов $\overline,$ $\overline$ и $\overline.$

  2.37. На плоскости заданы векторы $e_1(-1,2),$ $e_2(2,1)$ и $a(0,-2).$ Убедиться, что базис $B=e_1, e_2$ в множестве всех векторов на плоскости Построить заданные веткоры и найти разложение вектора $a$ по базису $B.$

  Ответ: $a=-\frace_1-\frace_2.$

  2.38. Показать, что тройка векторов $e_1(1,0,0), e_2(1,1,0)$ и $e_3(1,1,1)$ образуют базис в множестве всех векторов пространства. Вычислить координаты вектора $a=-2i-k$ в базисе $B(e_1, e_2, e_3)$ и написать соответствующее разложение вектора по базису.

  Читайте также:

    
  • Как сделать квала на фридом финанс
    
  • Как сделать текстуру normal bump
    
  • Как сделать напоминание в гугл календаре
    
  • Как сделать патреон
    
  • Как сделать перо из гарри поттера своими руками