Как сделать проверку матричного уравнения

Обновлено: 07.07.2024

Поскольку умножение матриц не всегда коммутативно, умножаем слева обе части уравнения на$ A^$.

$A^\cdot|A\cdot X = B$

$A^\cdot A\cdot X = A^\cdot B$

$I_\cdot X = A^\cdot B$

Решение уравнения имеет общий вид
$\color\cdot B>$

Пример 50
Решить уравнение
$\begin 1 & 3\\ 2 & 5 \end\cdot X \begin 3 & 5\\ 2 & 1 \end$

Убедимся, что первая матрица обратима.
$\left|A\right|=5-6=-1\neq 0$, следовательно, матрица обратима.

Умножаем слева на обратную ей матрицу.
$\begin 1 & 3\\ 2 & 5\\ \end^\cdot \begin 1 & 3\\ 2 & 5 \end\cdot X= \begin 1 & 3\\ 2 & 5 \end^\cdot \begin 3 & 5\\ 2 & 1 \end$

$I_\cdot X = \begin 1 & 3\\ 2 & 5 \end^\cdot \begin 3 & 5\\ 2 & 1 \end$

$\begin 1 & 3\\ 2 & 5 \end^= \begin -5 & 3\\ 2 & -1 \end\rightarrow X= \begin -5 & 3\\ 2 & -1 \end\cdot \begin 3 & 5\\ 2 & 1 \end= \begin -9 & -22\\ 4 & 9 \end$

XA = B, где матрица A обратима

Поскольку умножение матриц не всегда коммутативно, умножаем справа обе части уравнения на$ A^$.

$X\cdot A = B |\cdot A^$

$X\cdot A\cdot A^ = B\cdot A^$

$X \cdot I_ =B\cdot A^$

Решение уравнения имеет общий вид
$\color>$

Пример 51
Решить уравнение
$X \begin 1 & 3\\ 2 & 5\\ \end= \begin 3 & 5\\ 2 & 1\\ \end$

Убедимся, что первая матрица обратима.
$\left|A\right|=5-6=-1\neq 0$, следовательно, матрица обратима.

Умножаем справа на обратную ей матрицу.
$X \begin 1 & 3\\ 2 & 5 \end\cdot \begin 1 & 3\\ 2 & 5 \end^= \begin 3 & 5\\ 2 & 1 \end\cdot \begin 1 & 3\\ 2 & 5 \end^$

$X\cdot I_= \begin 3 & 5\\ 2 & 1 \end\cdot \begin 1 & 3\\ 2 & 5 \end^$

$\begin 1 & 3\\ 2 & 5 \end^= \begin -5 & 3\\ 2 & -1 \end\rightarrow X= \begin 3 & 5\\ 2 & 1 \end \cdot \begin -5 & 3\\ 2 & -1 \end= \begin -5 & 4\\ -8 & 5 \end$

Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку "Вычислить".

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Матричный метод решения систем линейных уравнений

Рассмотрим следующую систему линейных уравнений:

(1)

Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:

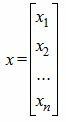(3)

Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.

Умножим матричное уравнение (2) на обратную матрицу A −1 . Тогда

A −1 Ax=A −1 b.

(4)

Учитывая определение обратной матрицы, имеем A −1 A=E, где E- единичная матрица. Следовательно (4) можно записать так:

Ex=A −1 b.

(4)

или, учитывая, что Ex=x:

x=A −1 b.

(5)

Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.

Примеры решения системы линейных уравнений матричным методом

Пример 1. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:

Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:

Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:

Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:

Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:

Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:

Делим каждую строку матрицы на ведущий элемент соответствующей строки:

Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

Пример 2. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :

Вычислим все алгебраические дополнения матрицы A:

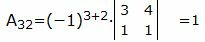Обратная матрица вычисляется из следующего выражения:

где A_ij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.

Используя формулу обратной матрицы, получим:

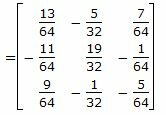Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A −1 b. Тогда

В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.

Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.

Найти решение системы n линейных уравнений с n неизвестными:

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n

Матричный вид записи: А × X = B

где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n - матрица системы.

X = x 1 x 2 ⋮ x n - столбец неизвестных,

B = b 1 b 2 ⋮ b n - столбец свободных коэффициентов.

Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A - 1 :

A - 1 × A × X = A - 1 × B .

Так как А - 1 × А = Е , то Е × X = А - 1 × В или X = А - 1 × В .

Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .

В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.

Пример решения системы линейных уравнений с помощью метода обратной матрицы

Решаем СЛАУ методом обратной матрицы:

2 x 1 - 4 x 2 + 3 x 3 = 1 x 1 - 2 x 2 + 4 x 3 = 3 3 x 1 - x 2 + 5 x 3 = 2

Записываем систему в виде матричного уравнения А X = B , где

А = 2 - 4 3 1 - 2 4 3 - 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .

d e t A = 2 - 4 3 1 - 2 4 3 - 1 5 = 2 × ( - 2 ) × 5 + 3 × ( - 4 ) × 4 + 3 × ( - 1 ) × 1 - 3 × ( - 2 ) × 3 - - 1 × ( - 4 ) × 5 - 2 × 4 - ( - 1 ) = - 20 - 48 - 3 + 18 + 20 + 8 = - 25

d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.

Находим обратную матрицу А - 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :

А 11 = ( - 1 ) ( 1 + 1 ) - 2 4 - 1 5 = - 10 + 4 = - 6 ,

А 12 = ( - 1 ) 1 + 2 1 4 3 5 = - ( 5 - 12 ) = 7 ,

А 13 = ( - 1 ) 1 + 3 1 - 2 3 - 1 = - 1 + 6 = 5 ,

А 21 = ( - 1 ) 2 + 1 - 4 3 - 1 5 = - ( - 20 + 3 ) = 17 ,

А 22 = ( - 1 ) 2 + 2 2 3 3 5 - 10 - 9 = 1 ,

А 23 = ( - 1 ) 2 + 3 2 - 4 3 - 1 = - ( - 2 + 12 ) = - 10 ,

А 31 = ( - 1 ) 3 + 1 - 4 3 - 2 4 = - 16 + 6 = - 10 ,

А 32 = ( - 1 ) 3 + 2 2 3 1 4 = - ( 8 - 3 ) = - 5 ,

А 33 = ( - 1 ) 3 + 3 2 - 4 1 - 2 = - 4 + 4 = 0 .

Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :

А * = - 6 7 5 17 1 - 10 - 10 - 5 0

Записываем обратную матрицу согласно формуле:

A - 1 = 1 d e t A ( A * ) T : А - 1 = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0 ,

Умножаем обратную матрицу А - 1 на столбец свободных членов В и получаем решение системы:

X = A - 1 × B = - 1 25 - 6 17 - 10 7 1 - 5 5 - 10 0 1 3 2 = - 1 25 - 6 + 51 - 20 7 + 3 - 10 5 - 30 + 0 = - 1 0 1

Обратные матрицы используются при решении матричных уравнений.

Простейшими матричными уравнениями называются соотношения вида: АХ=В и ХА=В, где А,В- известные матрицы, Х – неизвестная.

Если дано уравнение вида АХ=В, то решение выглядит так Х=А -1 В.

Если уравнение вида ХА=В, то Х=ВА -1 .

Непосредственной подстановкой легко установить, что найденное Х является решением соответствующего уравнения.

ПРИМЕРЫ: Решить матричные уравнения.

РЕШЕНИЕ:

Тогда нам дано уравнение вида ХА=В, следовательно Х=ВА -1 . Найдем A -1 .

Тогда нам дано уравнение вида АX=В, следовательно Х=А -1 B. Найдем A -1 .

Как вычислить определитель смотреть здесь.

Как умножать матрицы можно посмотреть здесь.

Как найти обратную матрицу можно посмотреть здесь.

В открывшемся окне:

Упражнения к уроку:

Решить матричные уравнения:

Автор: Аникина Анна

Комментарии к этой заметке:

Как можно решить логарифм матрицы простейшем способом?

все очень хорошо. Мог бы переслать Вам ,разработанный мной калькулятор для решения матричных уравнений, но не знаю как это исполнить.Хочется узнать Ваше мнение о нем

А как решить уравнение вроде ХА=В+2Х. Вот что делать с 2Х?

Доброго времени суток, Юлия! Необходимо представить 2Х=Х2Е (Е-единичная матрица соответствующего размера). А далее использовать свойства действий с матрицами.

Теорема 4.2 о существовании и единственности решения матричного уравнения (4.5). Если определитель матрицы .

В самом деле, подставляя в левую часть равенства (4.5), получаем , т.е. правую часть этого равенства.

Заметим, что решением матричного уравнения служит обратная матрица

где Теорема 4.3 о существовании и единственности решения матричного уравнения (4.6). Если определитель матрицы .

Заметим, что матрица является как бы "левым" частным от "деления" матрицы в (4.5) умножается на Пример 4.5. Даны матрицы

Решить уравнения: а) Решение. Обратная матрица была найдена в примере 4.2.

а) Решение уравнения

б) Уравнение не имеет решений, так как матрицы .

в) Решение уравнения

Пример 4.6. Решить уравнение: .

Решение. Преобразуя левую часть уравнения:

Пример 4.7. Решить уравнение , где

Решение. Обратные матрицы

были найдены в примерах 4.2, 4.3 соответственно. Решение уравнения находим по формуле

Пример 4.8. Решить уравнение

Решение. Определитель матрицы . Будем искать элементы матрицы . Подставляя в уравнение, получаем

Находим произведение, а затем приравниваем соответствующие элементы матриц в левой и правой частях уравнения:

Здесь, учитывая пропорциональность уравнений, в системе оставлены только два уравнения из четырех. Выразим неизвестные

Читайте также: