Как сделать правильный многогранник

Добавил пользователь Дмитрий К.
Обновлено: 04.10.2024

В школьной программе, к сожалению, сферическую геометрию и геометрию Лобачевского не изучают. Тем временем, их изучение совместно с Евклидовой геометрией, позволяет глубже понять происходящее с объектами. Например, понять связь правильных многогранников с разбиениями сферы, разбиениями плоскости Евклида и разбиениями плоскости Лобачевского.
Знания геометрии пространств постоянной кривизны помогает подниматься над трёхмерием и выявлять многогранники в пространствах размерности 4 и выше. Вопросы нахождения многогранников, нахождения разбиений пространств постоянной кривизны, вывода формулы двугранного угла правильного многогранника в n-мерном пространстве — так тесно переплетены, что выносить всё это в название статьи оказалось проблематично. Пусть в центре внимания будут, всем понятные, правильные многогранники, хотя они не только результат всех выводов, но и, одновременно, инструмент для постижения пространств высших размерностей и равномерно искривлённых пространств.

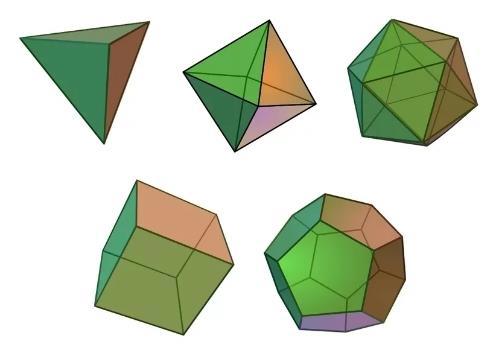
Для тех кто не знает (забыл) сообщаю (напоминаю), что в привычном нам трёхмерном Евклидовом пространстве всего пять правильных многогранников:

1. Тетраэдр:	2. Куб:	3. Октаэдр:	4. Додекаэдр:	5. Икосаэдр:

В трёхмерном пространстве правильным многогранником называется выпуклый многогранник, у которого все вершины равны между собой, все рёбра равны между собой, все грани равны между собой и грани являются правильными многоугольниками.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.

Вершины равны между собой означает, что количество рёбер и количество граней подходящих к каждой вершине одинаковое и подходят они под одинаковыми углами, в каждой вершине.

Оказывается, правильные многогранники удобно обозначать их символом Шлефли , характеризующим их комбинаторное строение. Который означает, что p1 угольники, сошлись по p2 штук в вершине. Т.е. по определению p1, p2 — целые числа, большие либо равные 3. Для тех кто не знаком с понятием Символ Шлефли написал отдельную статью с картинками Символ Шлефли. Часть 2.6

В такой записи наши многогранники получат обозначения:
1. Тетраэдр ,
2. Куб ,
3. Октаэдр ,
4. Додекаэдр ,
5. Икосаэдр
Например, — куб имеет 4 угольные грани, в каждой вершине сходится по 3 таких грани.
У октаэдра наоборот, грани 3 угольные, сходятся по 4 штуки в вершине.
Таким образом символ Шлефли полностью определяет комбинаторное строение многогранника.

Почему правильных многогранников всего 5? Может быть их больше?

Чтобы сполна дать ответ на этот вопрос, нужно сначала получить интуитивное представление о геометрии на сфере и на плоскости Лобачевского. Тем у кого такого представления ещё нет постараюсь дать необходимые объяснения.

Сфера

1. Что такое точка на сфере? Думаю, что всем интуитивно понятно. Мысленно не сложно представить точку на сфере.

2. Что такое отрезок на сфере? Берём две точки и соединяем их кратчайшим расстоянием на сфере, получится дуга, если смотреть на сферу со стороны.

3. Если продолжить этот отрезок в обе стороны, то он замкнётся и получится окружность. При этом плоскость окружности содержит центр сферы, это следует из того, что две исходные точки мы соединили кратчайшим, а не произвольным, расстоянием. Это со стороны она выглядит, как окружность, а в терминах сферической геометрии это прямая, так как была получена из отрезка, продолжением до бесконечности в обе стороны.

4. И, наконец, что такое треугольник на сфере? Берём три точки на сфере и соединяем их отрезками.

По аналогии с треугольником можно нарисовать произвольный многоугольник на сфере. Для нас принципиально важно свойство сферического треугольника, заключающееся в том, что сумма углов у такого треугольника больше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных сферических треугольников различна. Чем больше треугольник, тем БОЛЬШЕ у него сумма углов.

Соответственно, появляется 4-й признак равенства треугольников на сфере — по трём углам: два сферических треугольника равны между собой, если у них соответствующие углы равны.

Для простоты саму сферу проще не рисовать, тогда треугольник будет выглядеть немного раздутым:

Сферу ещё называют пространством постоянной положительной кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.

Лобачевский

Приступим. Плоскость Лобачевского будем представлять в интерпретации Пуанкаре II (Жюль Анри́ Пуанкаре́, великий французский учёный), эту интерпретацию геометрии Лобачевского ещё называют диском Пуанкаре.

1. Точка в плоскости Лобачевского. Точка — она и в Африке точка.

2. Отрезок на плоскости Лобачевского. Соединяем две точки линией по кратчайшему расстоянию в смысле плоскости Лобачевского.

Кратчайшее расстояние строится следующим образом:

Надо провести окружность ортогональную диску Пуанкаре, через заданные две точки (Z и V на рисунке). Центр этой окружности будет находиться всегда за пределами диска. Дуга соединяющая исходные две точки будет кратчайшим расстоянием в смысле плоскости Лобачевского.

3. Убрав вспомогательные дуги, получим прямую E1 — H1 в плоскости Лобачевского.

4. И наконец, что такое треугольник в плоскости Лобачевского? Берём три точки и соединяем их отрезками.

По аналогии с треугольником, можно нарисовать произвольный многоугольник на плоскости Лобачевского. Для нас принципиально важно свойство гиперболического треугольника, заключающееся в том, что сумма углов у такого треугольника всегда меньше 180 градусов, к которым мы привыкли в Евклидовом треугольнике. Более того, сумма углов у двух различных гиперболических треугольников различна. Чем больше треугольник по площади, тем МЕНЬШЕ у него сумма углов.

Соответственно, тут тоже имеет место 4-й признак равенства гиперболических треугольников — по трём углам: два гиперболических треугольника равны между собой, если у них соответствующие углы равны.

Плоскость Лобачевского (и вообще пространство Лобачевского любой размерности) ещё называют пространством постоянной ОТРИЦАТЕЛЬНОЙ кривизны. Кривизна пространства как раз и приводит к тому, что кратчайшим расстоянием является дуга, а не привычный нам прямолинейный отрезок. Отрезок как бы искривляется.

Правильные разбиения двумерной Сферы и правильные трёхмерные многогранники

Всё сказанное про сферу и плоскость Лобачевского относится к двумерию, т.е. поверхность сферы — двумерна. Какое это имеет отношению к трёхмерию, указанному в заголовке статьи? Оказывается, каждому трёхмерному правильному Евклидову многограннику взаимно однозначно соответствует своё разбиение двумерной сферы. Лучше всего это видно на рисунке:

Чтобы из правильного многогранника получить разбиение сферы, нужно описать вокруг многогранника сферу. Вершины многогранника окажутся на поверхности сферы, соединив эти точки отрезками на сфере (дугами), получим разбиение двумерной сферы на правильные сферические многоугольники. Для примера сделана видео демонстрация как икосаэдр соответствует разбиению сферы на сферические треугольники и обратно, как разбиение сферы на сферические треугольники, сходящиеся по пять штук в вершине, соответствует икосаэдру.

Чтобы по разбиению сферы построить многогранник, соответствующие дугам вершины разбиения нужно соединить обычными, прямолинейными, Евклидовыми отрезками.

Соответственно символ Шлефли икосаэдра — трёхугольники, сходящиеся по пять штук в вершине, задаёт не только структуру этого многогранника, но и структуру разбиения двумерной сферы. Аналогично и с другими многогранниками, их символы Шлефли задают и структуру соответствующих разбиений. Более того, разбиения плоскости Евклида и плоскости Лобачевского на правильные многоугольники, тоже можно задавать символом Шлефли. Например, — четырёхугольники, сходящиеся по четыре — это всем привычная нам тетрадь в клеточку, т.е. это разбиение плоскости Евклида на квадраты. А есть ли другие разбиения плоскости Евклида? Увидим дальше.

Построение разбиений двумерной сферы, плоскости Евклида и плоскости Лобачевского

Для построения разбиений двумерных пространств постоянной кривизны (таково общее название этих трёх пространств) нам потребуется элементарная школьная геометрия и знание того, что сумма углов сферического треугольника больше 180 градусов (больше Пи), что сумма углов гиперболического треугольника меньше 180 градусов (меньше Пи) и что такое символ Шлефли. Обо всём об этом уже сказано выше.

Итак, возьмём произвольный символ Шлефли , он задаёт разбиение одного из трёх пространств постоянной кривизны (для плоскости это верно, для пространств высших размерностей дело обстоит сложнее, но ничто нам не мешает исследовать все комбинации символа).

Рассмотрим правильный p1 угольник, проведём отрезки, соединяющие его центр и вершины. Получим p1 штук равнобедренных треугольника (на рисунке показан только один такой треугольник). Сумму углов каждого из этих треугольников обозначим за t и выразим t через пи и коэффициент лямда.

Тогда если лямда = 1, то треугольник Евклидов, т.е. находится в Евклидовой плоскости, если лямда в интервале (1, 3), то это значит, что сумма углов больше пи и значит этот треугольник сферический (не трудно представить, что при увеличении сферического треугольника в пределе получается окружность с тремя точками на ней, в каждой точке угол треугольника получается равным пи, а в сумме 3*пи. Это объясняет верхнюю границу интервала = 3). Если же лямда в интервале (0, 1), то треугольник гиперболический, так как сумма углов у него меньше пи (т.е. меньше 180 градусов). Коротко это можно записать так:

Не трудно посчитать, что:

С другой стороны, для сходимости в вершине p2 штук (т.е. целого числа) таких же многоугольников нужно, чтобы

Приравнивая выражения для 2*бетта, найденные из условия сходимости и из многоугольника:

Получили уравнение которое показывает какое из трёх пространств разбивает фигура заданная своим символом Шлефли . Для решения этого уравнения надо вспомнить, так же, что p1, p2 — целые числа, большие либо равные 3. Это, так сказать, следует из их физического смысла, так как это p1 угольники (не меньше 3 углов), сходящиеся по p2 штук в вершине (тоже не меньше 3, иначе это не вершина получится).

Решение этого уравнения заключается в переборе всех возможных значений для p1, p2 больших либо равных 3 и вычислении значения лямда. Если оно получится равным 1, то разбивает плоскость Евклида, если больше 1 но меньше 3, то это разбиение Сферы, если от 0 до 1, то это разбиение плоскости Лобачевского. Все эти вычисления удобно свести в таблицу.

Откуда видно, что:
1. Сфере соответствует всего 5 решений, когда лямда больше 1 и меньше 3, они выделены зелёным цветом в таблице. Это: — тетраэдр, — октаэдр, — икосаэдр, — куб, — додекаэдр. Их картинки были представлены в начале статьи.
2. Разбиениям Евклидовой плоскости соответствует всего три решения, когда лямда = 1, они выделены синим цветом в таблице. Вот как выглядят эти разбиения.

3. И наконец, все остальные комбинации соответствуют разбиениям плоскости Лобачевского, соответственно таких разбиений бесконечное (счётное) количество. Осталось только проиллюстрировать некоторые из них, для примера.

Среди моих читателей очень много воспитателей Детских садиков и руководителей Художественных кружков, в связи с этим, я изредка публикую посты с поделками вместе с детьми и для детей.

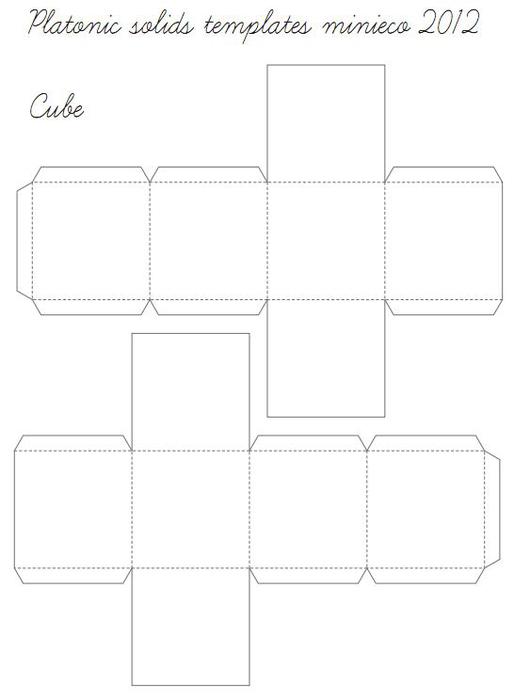
А сейчас, п редлагаю вам занять детей и сделать вместе с ними многогранники из цветной бумаги. Это не только увлечет их, они получат первые знания в математике. Ниже, под катом, пять шаблонов на некоторые многоугольники, которые нужно распечатать и увеличить. Все очень легко и просто, вырезать, согнуть и склеить. Очень красивая гирлянда, яркая, веселая и солнечная)

Можете сделать макет футбольного мяча. Для этого, желательно, взять бумагу - поплотнее.

Во вложении, шаблон мяча в натуральную величину, состоит из восьми страниц.

Тетраэдр, сделанный из бумаги или картона можно использовать в качестве модели, объясняя школьнику особенности этой фигуры в геометрии. Ещё самодельные объёмные фигуры можно использовать для декора комнаты или рабочего стола. Чтобы научиться делать тетраэдр своими руками, нужно прочесть несколько поэтапных инструкций по изготовления фигур из разных материалов.

Особенности фигуры, сколько граней и углов у тетраэдра

Тетраэдр – это объёмная геометрическая фигура треугольной формы. Она выглядит как пирамида. У тетраэдра 6 ребер, 4 вершины и 4 грани. Размеры и формы граней зависят от вида геометрической фигуры.

Какими бывают тетраэдры:

Что понадобиться, чтобы сделать тетраэдр своими руками

Перечень материалов и инструментов, необходимых для создания бумажного, либо картонного тетраэдра:

Желательно, чтобы бумага, на которой будет построен чертеж, была плотной. Подойдут листы для черчения, акварельная бумага или листы из альбома. Можно использовать бумагу для принтера, плотностью не менее 80 г/кв. м. Более тонкий материал будет плохо держать форму, а также рваться и мяться в процессе склеивания фигуры.

Как сделать из бумаги А4

Изготовление тетраэдра проходит в 5 этапов:

расчет размера;
подготовка шаблона из тонкого картона;
составление чертежа;
вырезание детали;
склеивание фигуры.

Расчет размера

Размер будущей фигуры зависит вида развертки. Грани можно расположить по кругу. В таком случае фигура получиться небольшой. Высота такого тетраэдра будет около 6 см. Если начертить горизонтальную развёртку, где грани будут расположены в таком порядке, что образуют фигуру в виде параллелограмма. В таком случае, можно получить более крупную фигуру.

Оптимальная длина ребра тетраэдра, начерченного в горизонтальной развертке на листе формата А4 – 10 см.

В итоге получится параллелограмм с диагональю равной 26,6 см. Размер листа формата А4 равен 21×29,7 см. Диагональ листа равна 36,4 см. Поэтому развертка с диагональю 26,6 см идеально поместиться на бумаге А4, и еще останется свободнее место, чтобы начертить полосы для склеивания фигуры.

Подготовка шаблона из картона

Из картона можно сделать шаблон 1 грани тетраэдра, чтобы потом было проще построить развертку.

Как сделать заготовку поэтапно:

На тонком картоне, с помощью линейки и простого карандаша, провести горизонтальную линию, равную длине ребра фигуры.
Приложить к левому концу линии транспортир. Поставить отметку на 60 градусах.
Приложить транспортир к правому углу линии, также отметить 60 градусов.
Через отметки провести 2 линии.
Измерить длину линий до места их пересечения. Все 3 стороны фигуры должны быть равны.

Ножницами аккуратно вырезать шаблон.

Построение развертки, чертежи

Как начертить круговую развертку тетраэдра с помощью картонного шаблона:

Ластиком удалить лишние линии.

Как начертить горизонтальную развертку тетраэдра, не используя картонный шаблон:

Когда чертеж будет готов, его нужно вырезать по контуру. Можно использовать ножницы или канцелярский нож.

Работа с готовой формой, склеивание

Склеить фигуру по вырезанной развертке несложно.

Порядок действий:

Большой тетраэдр из картона

Тетраэдр из картона (сделать поэтапно можно по инструкции, представленной далее в статье) получится крепким и будет хорошо держать форму. Размер объёмной фигуры зависит от вида картона.

Какой картон можно использовать для работы:

Не цветной картон после сборки тетраэдра можно покрасить или обклеить бумагой с узорами. Если на грани небольшой фигуры наклеить календарные листы или фотографии, можно получить необычное украшение для рабочего стола.

Особенности работы с жестким картоном

Тетраэдр из картона (сделать поэтапно развертку можно, не используя шаблоны) изготавливают следуя этим правилам:

Удобнее всего работать с двухслойным гофрированным картоном. Его можно вырезать из большой коробки, в которой перевозят бытовую технику. С картоном, сложенным в 3 и более слоя, работать будет намного сложнее. Такой материал плохо гнется и тяжело склеивается.

Подготовка и вырезание шаблона

Тетраэдр из картона (сделать поэтапно можно за 1 ч) можно изготовить, используя любой вид развертки. В этом мастер-классе описан процесс составления круговой развертки, без использования шаблона.

Порядок действий:

В центре картонного листа начертить горизонтальную линию, длина которой будет равна размеру ребра фигуры.
К левому концу линии приложить транспортир. Отметить 60 градусов.
Приложить транспортир к правому концу линии. Отметить 60 градусов.
Через отметки провести 2 линии до их пересечения. Должен получиться равносторонний треугольник.
От вершины треугольника, отложить 60 градусов с левой стороны. Начертить новый треугольник сбоку. 1 его сторона станет общей с уже начерченной фигурой.
Приложить транспортир к основе 1 фигуры. Отметить 60 градусов с обоих концов. Провести линии. Получилась 3 грань тетраэдра.
Последнюю грань начертить по аналогии, приложив транспортир к правой стороне нижнего треугольника.

на нижней стороне треугольника слева;
на левой стороне верхнего треугольника;
На правой стороне треугольника, расположенного справа.

Вырезать развертку канцелярским ножом.

Соединение граней

Как соединить грани фигуры:

Дождаться полного высыхания клея. Если остались излишки (застывшие капли или паутинки), их можно аккуратно срезать канцлерским ножом.

Научиться делать тетраэдр из бумаги или картона помогут инструкции, где все действия расписаны поэтапно. Главное, составить точный чертеж, а затем аккуратно вырезать развертку, используя подходящие инструменты.

Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.

В трёхмерном евклидовом пространстве существует всего пять правильных многогранников (упорядочены по числу граней):

упорядочены по числу граней):

Изображение	Правильный многогранник	Число вершин	Число рёбер	Число граней	Число сторон у грани	Число рёбер, примыкающих к вершине
тетраэдр	4	6	4	3	3	Td
гексаэдр	8	12	6	4	3	Oh
октаэдр	6	12	8	3	4	Oh
додэкаэдр	20	30	12	5	3	Ih
икосаэдр	12	30	20	3	5	Ih

Правильный многогранник может быть комбинаторно описан символом Шлефли , где:
p — число рёбер в каждой грани; q — число рёбер, сходящихся в каждой вершине.

Символы Шлефли для правильных многогранников приведены в следующей таблице:

Много-гранник		Вер- шины	Рёб-ра
тетраэдр	4	6	4
гексаэдр (куб)	8	12	6
октаэдр	6	12	8
додэкаэдр	20	30	12
икосаэдр	12	30	20

Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.

В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.

Огню соответствовал тетраэдр,

земле — гексаэдр,

воздуху — октаэдр,

воде — икосаэдр.

Аристотель добавил пятый элемент — эфир — и постулировал, что небеса сделаны из этого элемента, но он не сопоставлял его платоновскому пятому элементу.

Каждая из шести сфер соответствовала одной из планет (Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну). Многогранники были расположены в следующем порядке (от внутреннего к внешнему): октаэдр, за ним икосаэдр, додекаэдр, тетраэдр и, наконец, куб. Таким образом, структура Солнечной системы и отношения расстояний между планетами определялись правильными многогранниками. Позже от оригинальной идеи Кеплера пришлось отказаться, но результатом его поисков стало открытие двух законов орбитальной динамики — законов Кеплера, — изменивших курс физики и астрономии, а также правильных звёздчатых многогранников (тел Кеплера — Пуансо).

Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.

Читайте также: