Как сделать полукруг черчение
Добавил пользователь Алексей Ф. Обновлено: 05.10.2024
Из геометрии известно, что круг можно рассматривать как правильный многоугольник с большим количеством сторон. Следовательно, изометрическое изображение круга можно строить так же, описывая вокруг него квадрат (рис. 155, а). Точки касания А, В, С и D будут находиться на средине сторон квадрата и легко могут быть нанесены на аксонометрическое изображение (рис. 155, б). Промежуточные точки Е', F' и другие находим с помощью их координат. Изометрической проекцией круга является эллипс; его большая ось EG расположена под углом 60° к горизонту по большой диагонали ромба, а малая ось — под углом 30° по малой диагонали ромба.
Аксонометрические изображения круга чаще строят, проводя оси х и у через центр окружности (рис. 156, а); при этом отпадает надобность в построениях квадрата и ромба. Выбрав точку О', проводим через нее оси х' и у' (рис. 156, б), откладываем на осях величины, равные радиусу окружности, получаем точки А', В', С и D'. Другие точки находим с помощью их координат; построение точки Е показано двойными тонкими линиями. Два координатных отрезка для точки Е составляют так называемую координатную ломаную, которая будет в дальнейшем широко применяться при построении точек, расположенных в пространстве. Большая ось эллипса E'G' для круга, лежащего в плоскости х'О'у', расположена горизонтально, а малая ось — вертикально.
В начертательной геометрии доказывается, что отношение осей эллипса, являющегося изображением окружности, в прямоугольной изометрии равняется 0,58, т. е. если большую ось эллипса d принять за единицу, то малая ось будет равна 0,58d. Это положение иллюстрируем так: расположим плоскость квадрата, в который вписана окружность, параллельно плоскости П2 (рис. 157, а); повернем квадрат вокруг его горизонтальной диагонали на угол, равный 54° 30' (рис. 157, б); спроецируем квадрат и окружность на плоскость, параллельную горизонтальной диагонали квадрата (рис. 157, е). Диагональ ромба и горизонтальный диаметр окружности спроецируются при этом в действительную величину, стороны ромба изобразятся прямыми, составляющими =0,82 от величины d; наклоненные диагональ и диаметр окружности спроецируются с искажением и составят 0,58 от своей действительной величины, поскольку sin 35°30' = 0,58.
Зная эти зависимости, мы можем по заданному диаметру круга быстро найти размеры большой и малой осей эллипса, являющегося изометрической проекцией окружности. Пусть требуется построить прямоугольную изометрию круга, диаметр окружности которого равен 50 мм. Определяем размеры большой и малой осей эллипса: большая ось А'В' равна 50х X 1,22 = 61 мм, малая ось CD' равна 50'х0,71=35 мм. Строим по этим размерам оси эллипса на чертеже (рис. 158, а).
Из геометрического черчения известно (см. рис. 47), что по осям эллипса можно построить его кривую. Практически эллипс в изометрии обычно заменяют овалом, который строят следующим образом (рис. 158, б). На большой А'В' и малой CD' осях строим две окружности; они пересекают продолжение малой оси в точках 1 и 2, а большую ось — в точках 3 и 4; эти точки являются центрами для дуг овала; используя их, вычерчиваем овал с радиусами r = О'В'—О'С и R = CD' + г. Точку сопряжения дуг радиусов R и г находим, соединяя точки 1 и 4 прямой и продолжая эту прямую до пересечения с дугами в точке 5.
В прямоугольной изометрии все три эллипса одинаковы по форме, равны друг другу и лишь расположены различно. В отличие от этого в прямоугольной диметрии имеются две различные формы эллипса: одна для плоскости х'О'z', а другая — для плоскостей х'О'у' и z'O'y'.
Пусть требуется построить прямоугольную диметрию окружности, лежащей в плоскости хОz (рис. 159, а). Описываем вокруг окружности квадрат и проводим его диагонали. Отмечаем точки пересечения диагоналей с окружностью и координатные отрезки, нужные для построения точек Е, F и др. Строим квадрат в прямоугольной диметрии (рис. 159, б), проводим его средние линии А'С и B'D' и диагонали. Пользуясь координатными отрезками (помечены на чертежах тонкими двойными линиями), находим точки Е', F', G' и H'. Большая ось эллипса F'G' в прямоугольной диметрии будет равна l,06d, малая ось Е'Н' будет равна 0,95d (отношение 9 : 10). Полученные восемь точек соединяем от руки, а затем обводим по лекалу. Если требуется более точное построение, то находят с помощью координатных ломаных еще ряд промежуточных точек.
В практике эллипс нередко заменяют овалом (рис. 160, а). Центры дуг для построения овала находим так: строим ромб, его средние линии и диагонали, Из центра О' радиусом r=d/7 проводим вспомогательную окружность.
Она пересекает малую диагональ ромба в точках 1 и 2; используем эти центры для проведения дуг А'В' и CD'. Соединяем точки А' и I, С и 2; эти линии пересекают большую диагональ в точках 3 и 4. Пользуясь этими центрами, проводим дуги A'D' и В'С. При этом способе также не требуется откладывать размеры большой и малой осей; они получаются сами собой при проведении дуг.
Если требуется построить прямоугольную диметрию окружности, лежащей в плоскости х'О'у', то на осях х' и у' строим параллелограмм и намечаем средние точки его сторон (рис. 160, б). Затем через точку О' проводим горизонтальную прямую — направление большой оси эллипса. Откладываем на этой прямой размер большой оси эллипса, равный 1,06d. Перпендикулярно к ней проводим малую ось эллипса, размер которой равен 0,35d (отношение 3 : 10). Таким путем получаем восемь точек, принадлежащих эллипсу. В практике избегают построения параллелограмма и строят вместо эллипса овал по его осям А'В' и CD' (рис. 160, в). Последовательность построения такая: от центра О' на продолжении малой оси эллипса откладываем величину большой оси А'В'; получаем точку 1 — центр верхней дуги радиуса R. Тем же радиусом из точки 2 (не показана на чертеже) проводим нижнюю дугу овала. Слева и справа овал дочерчиваем кривыми радиуса r, величину которого принимаем равным r=O'C'/2 Центры 3 и 4 находим, делая засечки дугами r из точек А' и В'. Точку сопряжения 5 находим, соединяя прямой точки I и 4 и продолжая эту прямую до пересечения с дугой.
Окружность, находящаяся в плоскости, параллельной фронтальной плоскости проекций, проецируется на нее во фронтальной изометрической проекции в виде окружности (рис. 161, а), а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, — в эллипсы, большие оси которых наклонены к осям х' и z' под углами 22° 30'. Большие оси эллипсов равны 1,3 диаметра окружности, малые — 0,54 диаметра окружности.
Пусть требуется построить во фронтальной изометрии окружность диаметра 40 мм, находящуюся в плоскости х'О'у'. Определяем большую и малую оси эллипса. Большая ось А'В' = 1,3d = 1,3 40 = 52 мм, малая ось CD' = 0,54d = 0,54-40 = 21,6 мм. Овал, заменяющий собой эллипс, удобно строить из четырех центров радиусами, равными R = 1,3d и r = = 0,16d (рис. 161, б). В нашем примере R — 52 мм, г = 0,16d = 6,4 мм. Точка 5 — точка сопряжения.
Окружность, находящаяся в плоскости, параллельной горизонтальной плоскости проекций, проецируется на нее в горизонтальной изометрической проекции в виде окружности (рис. 161, б), а окружности, находящиеся в плоскостях, параллельных фронтальной и профильной плоскостям проекций, — в эллипсы. Большая ось эллипса, параллельного плоскости ?'?'z', наклонена к оси z' под углом 15° и равна l,37d; малая ось равна 0,37d. Большая ось эллипса, параллельного плоскости z'О'у', наклонена к оси у' под углом 30° и равна 1,22d; малая ось равна 0,71d (так же, как в прямоугольной изометрической проекции).
§ 18. Построение аксонометрических проекций плоских фигур и окружностей
Построение аксонометрических проекций плоских фигур и окружностей
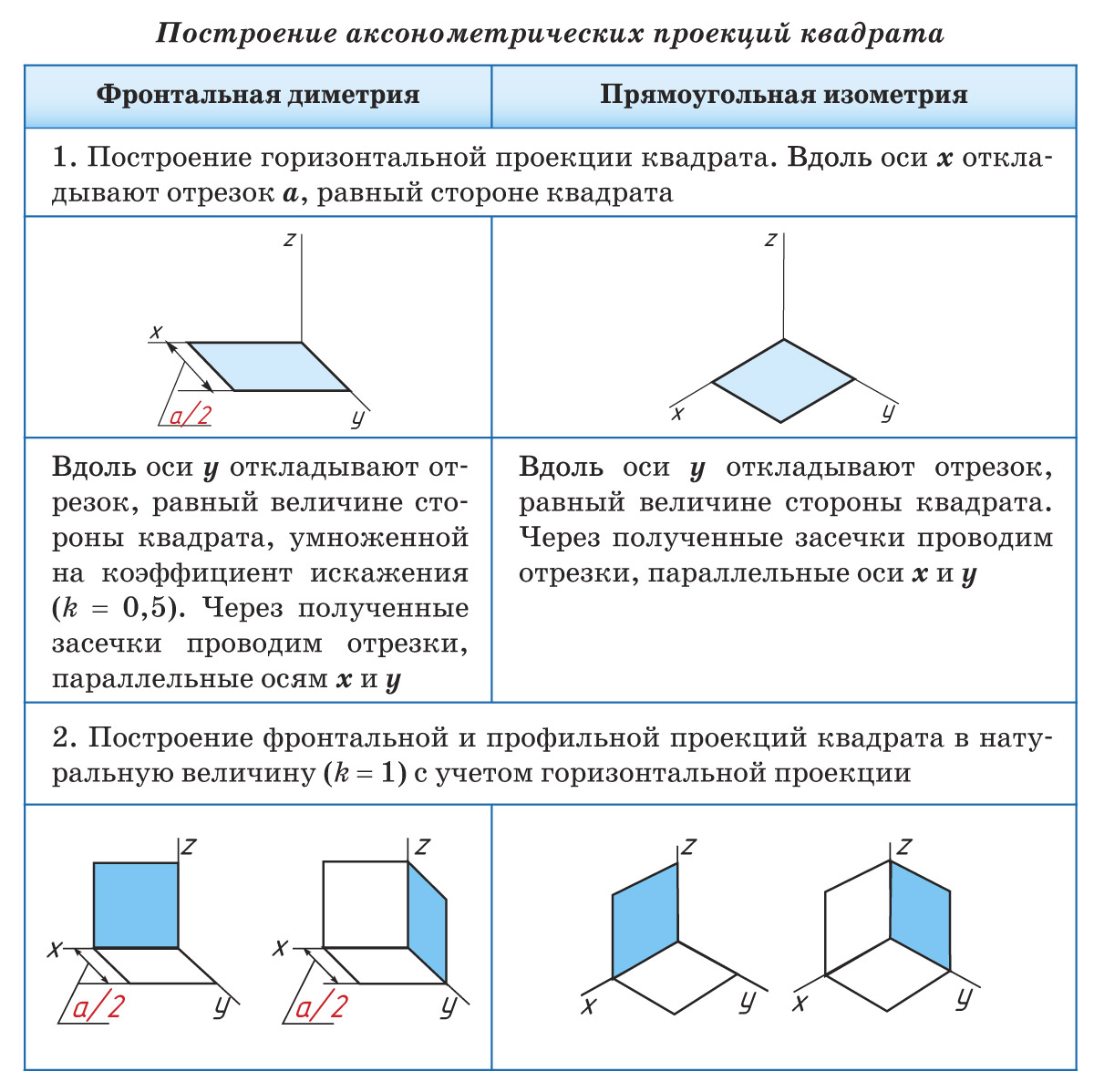
Построение аксонометрических проекций мы начнем с построения аксонометрических проекций плоских геометрических фигур. Знание приемов построения плоских фигур (квадрата, треугольника, прямоугольника, круга) необходимо для построения аксонометрических проекций геометрических тел, предметов и т. д.

Плоская фигура — фигура, все точки которой находятся в одной плоскости .
В качестве примера рассмотрим алгоритм построения аксонометрической проекции квадрата. По такому же алгоритму строятся аксонометрические проекции других плоских многоугольников.
.jpg)
На основе алгоритма построения квадрата постройте аксонометрические проекции прямоугольного треугольника. Какая сторона треугольника будет проецироваться с искажением во фронтальной диметрии?
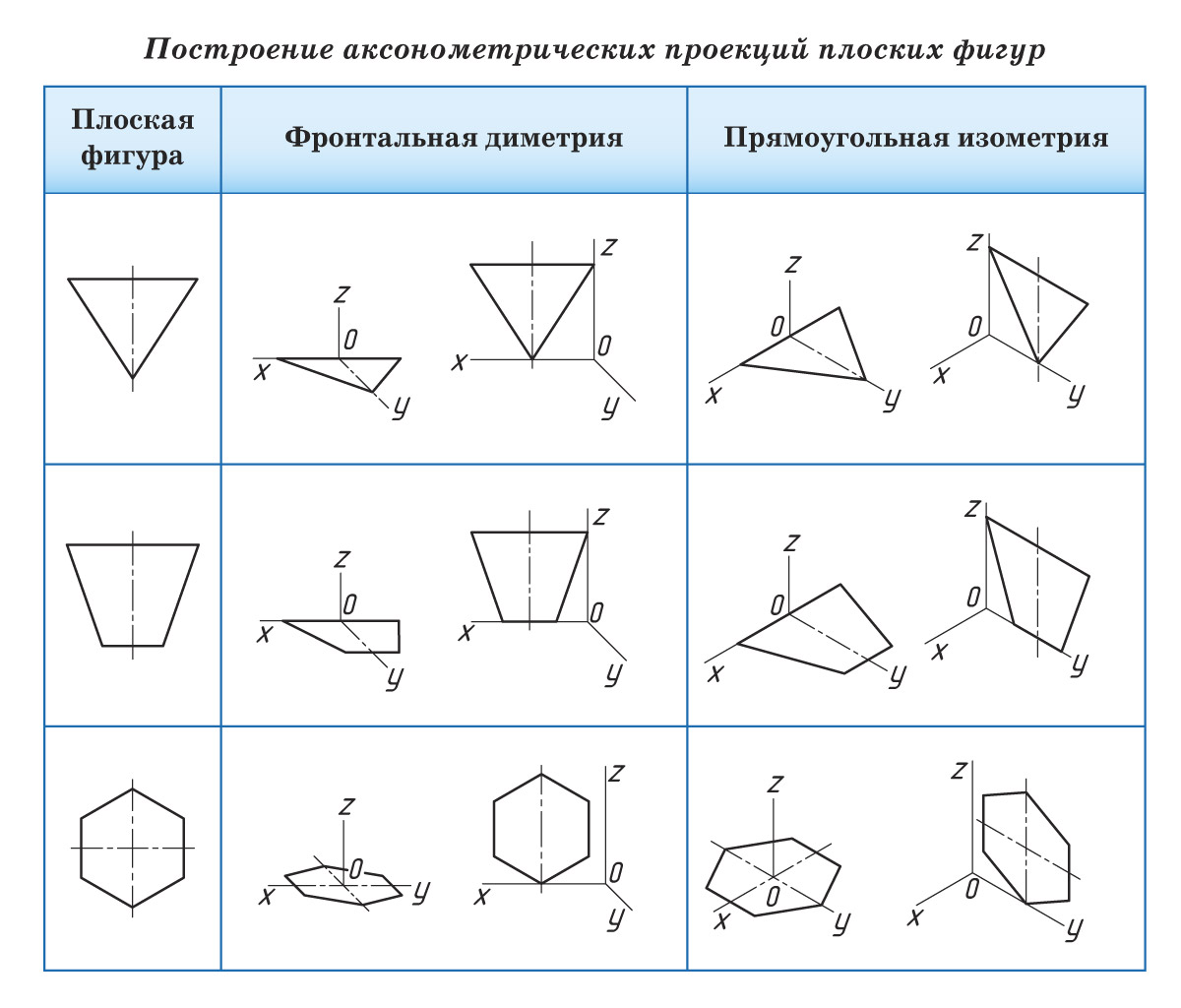

Постройте аксонометрические проекции елки. Какие плоские фигуры составляют изображение? Какой плоскости проецирования елка параллельна?
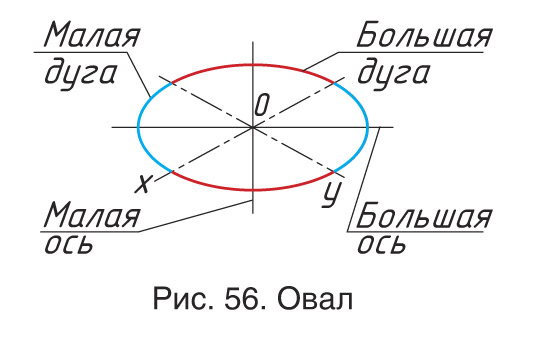
Кроме многоугольников, к плоским фигурам относят и окружности. В изометрической проекции окружность проецируется в замкнутую кривую линию — эллипс (рис. 55). Для его построения пользуются лекалами, поэтому эллипсы называют лекальными кривыми. Прием построения эллипса сложный и требует длительной работы, поэтому для упрощения построений эллипсы заменяют овалами.

Овал — замкнутая кривая, состоящая из четырех дуг окружностей, плавно переходящих друг в друга (рис. 56).
Для удобства построения овала в аксонометрической проекции сначала изображают аксонометрическую проекцию квадрата, построение которой вам уже известно.
Общее построение аксонометрической проекции окружности
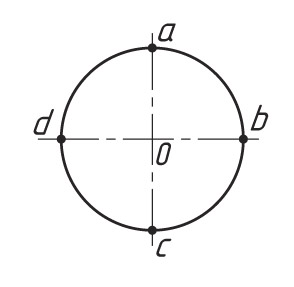
1. Выполняют построение осей аксонометрической проекции. Затем от точки О откладывают отрезки, равные радиусу окружности (R = Oa = Ob = Oc = Od). Через точки а, b, c и d проводят прямые, параллельные осям, получают ромб. Большая ось овала располагается на большой диагонали ромба.
2. Выполняют построение больших дуг овала. Из вершин А и В описывают дуги радиусом R, равные расстоянию от вершины (А или В) до точек a, b, c, d (R = Ad = Bb).
3. Строят малые дуги овала. Через точки B и a, B и b проводят прямые. На пересечении прямых Вa и Вb с большой диагональю ромба находят точки 1 и 2. Они будут центрами малых дуг. Их радиус R1 равен 1а или 2b
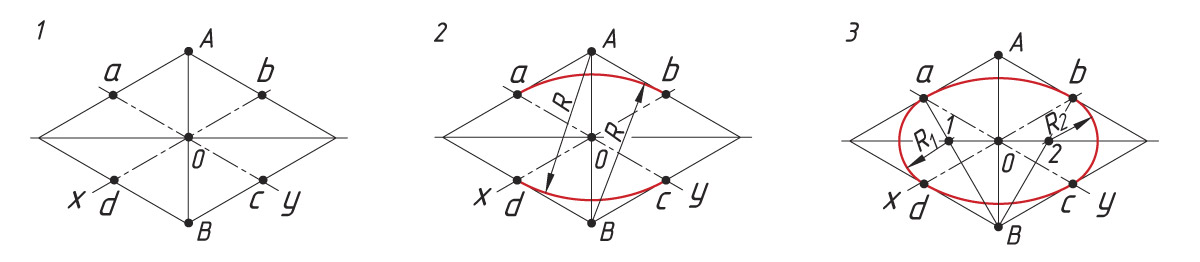
Построение фронтальной и профильной проекций окружности
Фронтальная и профильные проекции окружности выполняются по такому же алгоритму, как и горизонтальная проекция.

Помните! Большая ось овала всегда перпендикулярна аксонометрической оси, не участвующей в образовании плоскости, на которой ведется построение. Малая ось — продолжение аксонометрической оси.

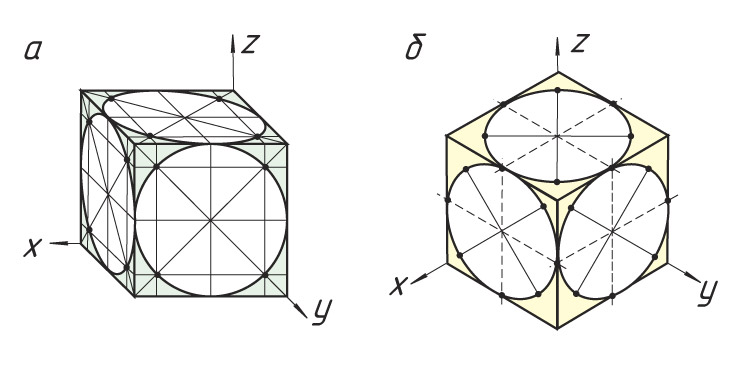
Определите, на каком рисунке (а или б) изображен куб в изометрии. Объясните, как вы это определили.

Эллипсограф, или Сеть Архимеда, — механизм, который способен преобразовывать возвратно-поступательное движение в эллипсоидное. Применяется в качестве чертежного инструмента для вычерчивания эллипсов, а также в качестве приспособления для разрезания стекла, бумаги, картона. История этого механизма точно не определена, но считается, что эллипсографы существовали еще во времена Архимеда.

Постановка задачи
Вначале определимся с тем, что будем строить. Для примера предлагаю взять полуокружность радиуса 10 мм с центром в точке с координатами (100, 100). Данная дуга показана на рисунке ниже.

(Картинка кликабельна).
A, B и C – вспомогательные точки, которые пригодятся нам при описании различных способов построения дуги.
По трем точкам
Первый способ основывается на том, что вам известны координаты точек A, B и C, но неизвестны координаты центра. Для построения дуги по трем точкам используется метод ksArcBy3Points интерфейса ksDocument2D. Ниже приводится его прототип.
Стили линии обсуждались в предыдущей статье цикла.
В случае успеха метод возвращает указатель на построенную дугу, а в случае ошибки – значение ноль.
Для построения нашей дуги нужно определиться с координатами точек. Так, точка A имеет координаты (90, 100), точка B (100, 110), точка C (110, 100). При таких исходных данных вызов метода ksArcBy3Points должен производиться так, как показано ниже.
О том, как получить указатель на интерфейс ksDocument2D, рассказывалось в предыдущих статьях цикла.
По центру и углам
Данный способ основан на том, что вам известны координаты центра дуги и углы ее концов. Для построения дуги по этой информации используется метод ksArcByAngle интерфейса ksDocument2D. Ниже приводится прототип этого метода.
С параметрами xc, yc, rad и style, думаю, всё ясно. С ними вопросов возникнуть не должно.
Параметры f1 и f2 задают углы (в градусах) между прямыми, проходящими через центр дуги и ее конечные точки, и горизонтальной прямой. Данные углы показаны на рисунке ниже.

Теперь по поводу параметра direction. Он задает направление, в котором следует отрисовывать дугу. Если он равен 1, то дуга строится против часовой стрелки, если же он равен -1, то дуга строится по часовой стрелке. Например, дуга, изображенная на рисунке выше, отрисована против часовой стрелки, а на рисунке ниже представлена дуга, построенная с теми же параметрами, но по часовой стрелке.

В случае успеха метод ksArcByAngle возвращает указатель на построенную дугу, а в случае ошибки — значение ноль.
Вернемся к нашей задаче построения дуги. Для ее отрисовки против часовой стрелки углы должны быть заданы следующим образом: f1 = 0, f2 = 180. Для отрисовки этой же дуги по часовой стрелке значения углов нужно поменять местами (f1 = 180, f2 = 0).
Код построения дуги приведен ниже.
По центру и конечным точкам
Данный способ основан на том, что вам известны координаты центра дуги и координаты конечных точек дуги. Для построения дуги по этой информации используется метод ksArcByPoint интерфейса ksDocument2D. Ниже приводится прототип этого метода.
Данный метод очень похож на рассмотренный ранее метод ksArcByAngle. Разница состоит лишь в том, что конечные точки задаются не углами, а координатами.
В случае успеха метод ksArcByPoint возвращает указатель на дугу, а в случае ошибки — ноль.
Ниже приводится код вызова этого метода для построения нашей дуги.
Внимательный читатель наверняка заметил, что параметры метода ksArcByPoint являются избыточными. Почему? Неужели ошибка создателей API? На самом деле нет. Просто нужно правильно понимать назначение точек (x1, y1) и (x2, y2). Согласно документации КОМПАС:
x1, y1 – координаты начальной точки дуги,
x2, y2 – координаты конечной точки дуги.
Такое неправильное описание и создает путаницу. На самом деле точки (x1, y1) и (x2, y2) могут не принадлежать дуге. Они задают не положение конечных точек, а ориентацию вектора, на котором они находятся. Причем начало этого вектора находится в центре дуги. Рисунок ниже поясняет это более наглядно.

Исходя из этого, рассматриваемую нами дугу можно построить с помощью кода, приведенного ниже.
Обратите внимание: конечные точки не совпадают с точками A и C, но дуга все равно строится правильно.
Заключение
В данной статье мы рассмотрели различные способы построения дуги окружности. Каким из них пользоваться, решайте сами. Но я думаю, что ваше решение будет определяться той информацией о дуге, которая у вас есть в данный момент времени.
Продолжение следует, следите за новостями блога.
Помогите пожалуйста нарисовать полукруг в Word 2010. не могу допереть как его нарисовать, знаю про узлы которые можно корректировать для каждой фигуры, однако они не помогают , все получается коряво.
Заранее спасибо!
Рисование в word
Всем привет ;) Вопрос наверно настолько глуп, что даже сложно его сформулировать. Но может кто.
Рисование в MS Word 2010
Никак не пойму, какие тут надо задавать x, y, z: Спасибо.
Рисование полукруга
В общем проблема состоит в том что надо сделать так чтобы на комплексном чертеже(левом где косые.
Отрисовка полукруга
День добрый! Хочу перенести текст над картинкой на саму картинку, делаю так: .pic < .
Решение
Решение
Создание полукруга
Помогите, пожалуйста, нарисовать полукруг с пользовательскими данными)
Движение полукруга
Надо чтобы полукруг двигался по полукругу. или скажите хоть примерно че делать
Перемещение полукруга по экрану
Помогите,пожалуйста, написать программу в С++ перемещения полукруга по экрану. По нажатию клавиш.

Поворот полукруга по часовой стрелке
Добрый день! Нужно сделать так чтоб полукруг крутился по часовой стрелке и чтобы он постепенно.
Читайте также:

