Как сделать площадь треугольника

Обновлено: 07.07.2024

Треугольник - это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.

Высота треугольника - это перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

По типовым особенностям формы, треугольники бывают разносторонние, прямоугольные, равнобедренные, равносторонние.

Формула площади треугольника

Посчитать площадь треугольника можно разными способами. Это зависит от формы треугольника и известных размеров. Так есть типовые расчёты площади для прямоугольного, равнобедренного и равностороннего треугольников.

Площадь треугольника расчитывается по размерам трёх сторон по формуле Герона или через основание и высоту треугольника.

С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть смотрите ниже.

Площадь треугольника по основанию и высоте

Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом "высота" понимают высоту треугольника, проведенную к основанию (Рис.1):

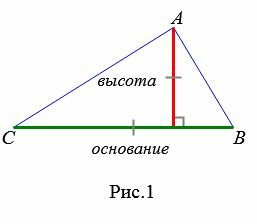Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.

Доказательство. Пусть AC основание треугольника ABC (Рис.2).

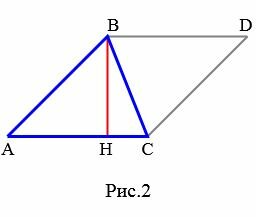Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что

Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку \( \small AC \ || \ BD \) и \( \small AB\ || \ CD \), то ABDC является параллелограммой и, следовательно, \( \small AC \ = \ BD \), \( \small AB\ = \ CD . \) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма ABDC равна \( \small S_=AC \cdot BH, \) то площадь треугольника ABC (и BCD)равна половине площади параллелограмма:

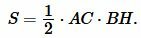Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.

Доказательство. Пусть площадь треугольников ABC и A₁B₁C₁ равны:

где AC и A₁C₁ основания треугольников ABC и A₁B₁C₁, соответственно, а h их высоты.

Обозначим через k отношение

То есть отношение площадей треугольников с равными высотами равно отношению их оснований.

Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.

Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.

Площадь треугольника по двум сторонам и углу между ними

Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что

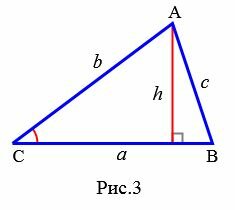Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):

где h − высота треугольника.

Подставляя (2) в (1), получим:

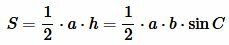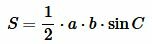(3)

Площадь треугольника по стороне и прилежащим двум углам

Пусть известна сторона треугольника и две прилежащие углы (Рис.4).

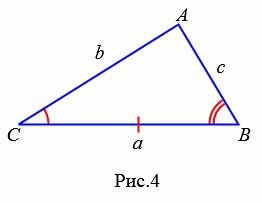Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:

Найдем сторону b используя теорему синусов:

В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:

.

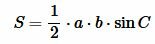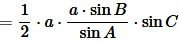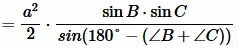Площадь треугольника по трем сторонам. Формула Герона

Для нахождения площади треугольника по трем сторонам используют формулу Герона:

где a, b, c − стороны треугольника, а p − полупериод треугольника:

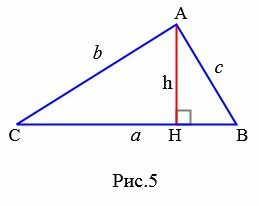Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:

Из (8) и (9) следует:

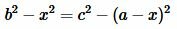Откуда находим x:

Подставляя (10) в (8) найдем h:

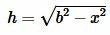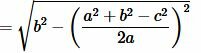(11)

Тогда площадь треугольника равна:

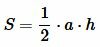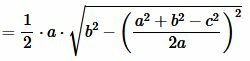(12)

Преобразовав (12) получим формулу (7):

.

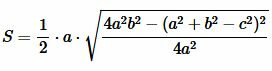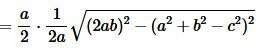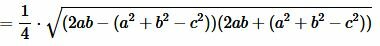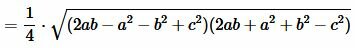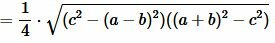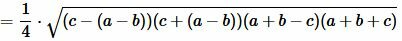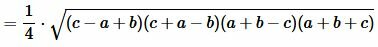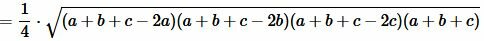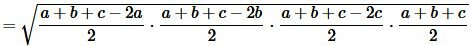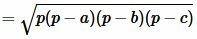Площадь треугольника по трем сторонам и радусу описанной окружности

Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.6). Докажем, что площадь треугольника равна: \( \small S=\frac<\large abc><\large 4R>. \)

Основанием треугольника может быть выбрана любая из сторон треугольника.

По двум сторонам и углу между ними

Угол α между сторонами может быть любым: тупым, острым, прямым.

По радиусу вписанной окружности и трем сторонам

По радиусу описанной окружности и трем сторонам

По формуле Герона

По стороне и двум прилежащим углам

Для равнобедренных треугольников

По боковым сторонам и основанию

По боковым сторонам и углу между ними

По боковой стороне, основанию и углу между ними

По основанию и углу между боковыми сторонами

По высоте и основанию

Для равносторонних треугольников

По стороне

По высоте

По радиусу вписанной окружности

По радиусу описанной окружности

Для прямоугольных треугольников

По двум катетам

Через гипотенузу и угол

Через катет и угол

По отрезкам, на которые делит гипотенузу вписанная окружность

Через гипотенузу и вписанную окружность

По формуле Герона

Таблица с формулами площади треугольника

Определения

Катет

Катет — одна из двух сторон прямоугольного треугольника, образующих прямой угол. Противолежащая прямому углу сторона называется гипотенузой. Для непрямоугольного треугольника катеты не существуют.

Треугольник

Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью (например, для определения понятия площади).

Площадь

Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.

Площадь треугольника определяется как общее пространство, занимаемое тремя сторонами треугольника в 2-мерной плоскости. Основная формула для площади треугольника равна половине произведения его основания и высоты, то есть A = 1/2 × b × h. Эта формула применима ко всем типам треугольников, будь то разносторонний треугольник, равнобедренный треугольник или равносторонний треугольник. Следует помнить, что основание и высота треугольника перпендикулярны друг другу.

В этом уроке мы изучим формулы площади треугольников для различных типов треугольников, а также некоторые примеры.

Что такое площадь треугольника?

Площадь треугольника — это область, заключенная между сторонами треугольника. В зависимости от длины сторон и внутренних углов, площадь треугольника варьируется от одного треугольника к другому. Единица площади измеряется в квадратных единицах, например м 2 , см 2 и т. Д.

Треугольник – это геометрическая фигура, которая состоит из трех сторон, образованных путем соединения трех точек на плоскости, не принадлежащих одной прямой.

• Общие формулы расчета площади треугольника
  • По основанию и высоте
  • Формула Герона
  • Через две стороны и угол между ними
  • Через длину стороны
  • Через высоту

  Общие формулы расчета площади треугольника

  По основанию и высоте

  Площадь (S) треугольника равняется половине произведения его основания и высоты, проведенной к нему.

  
  

  Формула Герона

  Для нахождения площади (S) треугольника необходимо знать длины всех его сторон. Считается она следующим образом:

  
  

  p – полупериметр треугольника:

  Через две стороны и угол между ними

  Площадь треугольника (S) равняется половине произведения двух его сторон и синуса угла между ними.

  
  

  Площадь прямоугольного треугольника

  Площадь (S) фигуры равняется половине произведения его катетов.

  
  

  Площадь равнобедренного треугольника

  Площадь (S) рассчитывается по следующей формуле:

  
  

  Площадь равностороннего треугольника

  Чтобы найти площадь правильного треугольника (все стороны фигуры равны), необходимо воспользоваться одной из формул ниже:

  Через длину стороны

  
  

  Через высоту

  
  

  Примеры задач

  Задание 1
  Найдите площадь треугольника, если одна из его сторон равна 7 см, а высота, проведенная к ней – 5 см.

  Решение:
  Используем формулу, в которой участвуют длина стороны и высота:
  S = 1/2 ⋅ 7 см ⋅ 5 см = 17,5 см 2 .

  Задание 2
  Найдите площадь треугольника, стороны которого равны 3, 4 и 5 см.

  Решение 1:
  Воспользуемся формулой Герона:
  Полупериметр (p) = (3 + 4 + 5) / 2 = 6 см.

  Решение 2:
  Т.к. треугольник со сторонами 3, 4 и 5 – прямоугольный, его площадь можно посчитать по соответствующей формуле:
  S = 1/2 ⋅ 3 см ⋅ 4 см = 6 см 2 .

  Читайте также:

    
  • Как сделать уведомление в 1с
    
  • Как сделать свое приветствие в termux
    
  • Как сделать справку о кодировке от алкоголизма в интернете самому бесплатно со своим именем
    
  • Как сделать слабый раствор йода по биологии
    
  • Как сделать перекрут яичка