Как сделать параболу

Добавил пользователь Дмитрий К.
Обновлено: 04.10.2024

Timeweb - компания, которая размещает проекты клиентов в Интернете, регистрирует адреса сайтов и предоставляет аренду виртуальных и физических серверов. Разместите свой сайт в Сети - расскажите миру о себе!

Виртуальный хостинг

Быстрая загрузка вашего сайта, бесплатное доменное имя, SSL-сертификат и почта. Первоклассная круглосуточная поддержка.

Производительность и масштабируемые ресурсы для вашего проекта. Персональный сервер по цене виртуального хостинга.

Выделенные серверы

Парабола - график квадратичной функции вида $f(x)=ax^2+bx+c$ . Состоит данный график из вершины и ветвей.

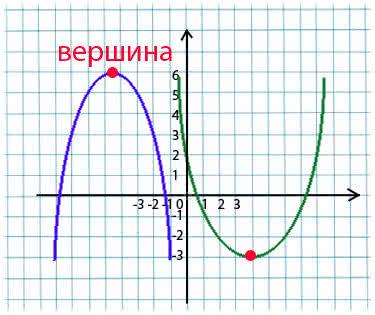
При этом $a\neq0$ , иначе функция уже будет не квадратичной, а линейной.

Формула параболы может рассказать нам о многом:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Коэффициент $a$ говорит о направлении ветвей параболы. Если $а>0$ , то ветви смотрят вверх, если \(а , вниз.
От параметра $b$ зависит вершина параболы. Она рассчитывается по формуле: $x_в=\frac$
Свободный член $с$ отвечает за пересечение параболы с осью $y$ .

Алгоритм построения параболы

Построим график функции $f(x)=ax^2+bx+c.$

Определим куда смотрят ветви параболы.
Найдем вершину по формуле $x_в=\frac$ . Подставим $x_в$ в формулу функции и получим значение $y_в$ . Таким образом мы имеем обе координаты вершины. Нанесем их на систему координат.
Найдем точку пересечения с осью y по параметру с и нанесем на чертеж точку, симметричную ей, относительно оси симметрии параболы, т.е. прямой $y=\frac.$
Далее решаем уравнение $ax^2+bx+c=0$ . Получаем корни - они являются точками пересечения параболы с осью $x$ . Если они рациональны, наносим их на чертеж, в обратном случае, они не пригодятся.
Затем считаем значения функции в дополнительных симметричных точках и соединяем все найденные точки.

Примеры решения задач на построение параболы

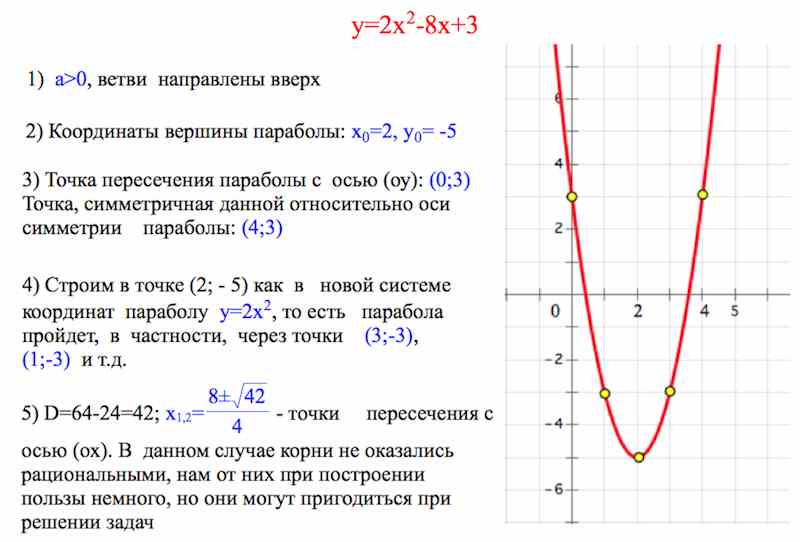
Смещение параболы

Свободный член с смещает параболу по оси y. Например, если c=2, то парабола f(x)=ax^2+bx сместится вверх на 2 единичных отрезка, а если с=-2, то график сместится вниз так же на 2 единичных отрезка.

В случае, когда к аргументу x прибавляется или вычитается какое-либо число, график смещается по оси x. Например, для построения графика функции $y=^2$ достаточно сместить график $y=x^2 $ на 4 единичных отрезка влево, а для построения графика $y=^2$ нужно сместить график $y=x^2$ на 3 единичных отрезка вправо.

Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.

Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.

График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле

$<x_o> = \frac>>,$

для нахождения ординаты можно подставить в формулу y=x²+bx+c вместо каждого x найденное значение хₒ: yₒ = x ₒ ²+bx ₒ +c . От вершины ( хₒ ; y ₒ ) строим параболу y=x ² .

Построить график функции y=x²+2x-3.

y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы

$<x_o> = \frac>> = \frac>> = - 1,$

$<y_o> = <( - 1)^2>+ 2 \cdot ( - 1) - 3 = - 4.$

От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).

График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².

Построить график функции y= -x²+2x+8.

y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы

$<x_o> = \frac>> = \frac><<2\cdot( - 1)>> = 1,$

$<y_o> = - + 2\cdot1 + 8 = 9.$

От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):

Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или — x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.

Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии) . Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.

Построить график функции y=x²+5x+4.

y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы

$<x_o> = \frac>> = \frac>> = - 2,5;$

$<y_o> = <( - 2,5)^2>+ 5 \cdot ( - 2,5) + 4 = - 2,25,$

то есть вершина параболы — точка (-2,5; -2,25).

Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).

В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).

Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:

Построить график функции y= -x²-3x.

y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы

$<x_o> = \frac>> = \frac>> = - 1,5;$

$<y_o> = - <( - 1,5)^2>- 3 \cdot ( - 1,5) = 2,25.$

Вершина (-1,5; 2,25) — первая точка параболы.

В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x =0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.

При х=1 y=-1²-3 ∙ 1=-4, то есть (1; -4) — дополнительная точка для построения графика.

Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.

Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x ² +c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где называется квадратичной функцией.

В уравнении квадратичной функции:

a - старший коэффициент

b - второй коэффициент

с - свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками - это, так называемые "базовые точки". Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.

График функции имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .

Если старший коэффициент a , то ветви параболы напрaвлены вниз .

Второй параметр для построения графика функции - значения х, в которых функция равна нулю, или нули функции. На графике нули функции - это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:

2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:

3 . Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

>/" />
, >/" />

Если ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции - координаты вершины параболы:

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции - точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

=7" />

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

/4=1" />
, /4=-2,5" />

3. Координаты вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2 . Уравнение квадратичной функции имеет вид - в этом уравнении - координаты вершины параболы

или в уравнении квадратичной функции , и второй коэффициент - четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

сначала построить график функции ,
затем одинаты всех точек графика умножить на 2,
затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент - четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции - точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
- ширины графика функции от значения коэффициента ,
- сдвига графика функции вдоль оси от значения ,

- сдвига графика функции вдоль оси от значения
- направления ветвей параболы от знака коэффициента
- координат вершины параболы от значений и :

И.В. Фельдман, репетитор по математике.

Читайте также: