Как сделать одночлен стандартного вида

Обновлено: 07.07.2024

§ 8. Тема урока: Одночлен и стандартный вид одночлена.

Понятие одночлена

Среди них содержатся: числа, переменные, выражения, противоположные переменным (т.е. с противоположным знаком), а также степени чисел и переменных и их произведения. Такие выражения называют одночленами.

Любая сумма, разность, частное — не является одночленом. Например, выражения:

не являются одночленами.

Не является одночленом и выражение $(a+b)^,$ так как представляет собой степень суммы, а не степень переменной или числа. Также не является одночленом выражение $\frac,$ так как представляет собой частное, но оно в отличие от рассмотренных выше может быть представлено в виде произведения числа $\frac$ и переменных $p$ и $q,$ то есть в виде одночлена $\fracpq.$

Стандартный вид одночлена

Одночлен $\textcolor$ можно представить в различных видах. Например, как $\textcolor$ или $-15a^x^.$ Одночлен $-15a^x^$ отличается от одночленов $\textcolor$ и $\textcolor$ тем, что он имеет один числовой множитель, стоящий на первом месте, и каждое произведение одинаковых переменных в нем представлено степенью. Такой вид одночлена называют стандартным.

Определение:
Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.

Одночлены такие, как $abc$ и $-x^,$ не содержат числовых множителей. Тем не менее их относят к одночленам, имеющим стандартный вид. Считают, что коэффициентами этих одночленов служат числа $1$ и $-1,$ так как $abc=1\cdot abc$ и $-x^=(-1)\cdot x^.$

Приведем примеры одночленов, представленных в стандартном виде:

Приведение одночлена к стандартному виду есть тождественное преобразование, выполняемое на основании определения степени или свойств степени (см. свойства степени), переместительного и сочетательного законов умножения.

Как привести одночлен к стандартному виду?

Пусть составлена задача привести одночлен $ 3ab^\cdot 5a^b $ к стандартному виду.

Используя переместительный и сочетательный законы умножения, выполним преобразование:

Применив основное свойство степени, получим:

Одночлен $ 3ab^\cdot 5a^b $ с помощью законов действий и свойств степени мы привели к стандартному виду $ 15a^b^. $

Подобные одночлены

Более подробно подобные одночлены мы рассмотрим в следующей статье.

Понятие о степени одночлена

В одночлене $ 5x^ $ переменная $ x $ во второй степени, а в одночлене $ 3,7x^ $ — в пятой степени. Говорят, что одночлен $ 5x^ $ — второй степени, а одночлен $ 3,7x^ $ — пятой степени.

Если одночлен содержит несколько переменных, то степень такого одночлена условились считать равной сумме показателей степеней этих переменных.

Например, одночлен $ 8x^y^z $ имеет шестую степень, так как сумма показателей входящих в него переменных равна $ 3+2+1=6. $ Степень одночлена — $ 0,9ab $ равна двум, одночлена — $ \fracm^n^ $ — девяти.

Всякое число является одночленом. Степень такого одночлена договорились считать равной нулю.

Исключение составляет число нуль. Этому одночлену не приписывается никакой степени. Целесообразность такого исключения будет выяснена в дальнейшем.

По определению полагают, что при $ x\not =0, \ x^=1. $

Отсюда следует, что, например, число $ 5 $ можно представить в виде $ 5x^ $ или в виде $ 5a^b^. $

Степень каждого из одночленов $ 5x^ $, $ 5a^b^ $ и, следовательно, одночлена $ 5 $ равна нулю.

Такое определение степени с показателем, равным нулю, естественно. Если мы хотим приписать смысл выражению $ a^ $, где $ a\not =0, $ и чтобы при этом сохранилось основное свойство степени $ a^a^=a^, $ мы должны положить, что $ a^=1. $ Действительно, потребовав сохранения основного свойства степени, получим для любого $ n\in ℕ $ и $ a\not =0: $

\[ a^a^=a^=a^. \]

Отсюда $ a^ $ необходимо должно быть равным единице.

Выражению $ 0^ $ не приписывается никакого смысла.

Задачи и примеры решений

Какие выражения называют одночленами?

Объясните, какой вид одночлена называют его стандартным видом.

Одночлен — это алгебраическое выражение, представляющее собой число, переменную, их степени с натуральным показателем, а также любые произведения, составленные из них.

Пример. 12, , m, (-2) 3 , a 2 , 5abc, a 3 x, 3,7c(-2ab 2 ) — одночлены.

Выражения x + 2 или не являются одночленами, так как представляют сумму или частное переменных и числа.

Число 0 называют нулевым одночленом.

Буквы и числа одночлена, представляющего собой произведение, называют множителями данного одночлена. При этом числа называют числовыми множителями одночлена, а буквы — буквенными множителями одночлена.

Пример. Назовите числовые и буквенные множители одночлена 5abc.

Множителями данного одночлена являются число 5 и буквы a, b, c:

Числовой множитель: 5.

Буквенные множители: a, b, c.

Стандартный вид одночлена

Стандартный вид одночлена — это запись одночлена, представляющая собой число, степень переменной или произведение, в котором только один числовой множитель, записанный на первом месте, а каждая его буква участвует в его записи лишь один раз, при этом буквы записаны в алфавитном порядке.

Пример. 7, a, -3xy 2 , 1abс — одночлены стандартного вида.

А вот следующие одночлены записаны не в стандартном виде:

12aa 3 b и 4cb(−2)y,

так как первый содержит одинаковые буквы, а во втором два числовых множителя и буквенные множители записаны не в алфавитном порядке.

Стандартный вид нулевого одночлена есть 0.

Коэффициент одночлена

Коэффициент одночлена — это числовой множитель в одночлене стандартного вида, который содержит хотя бы одну переменную. Понятие коэффициент также относят к одночленам стандартного вида, представляющим собой числа без буквенных множителей. Коэффициентами таких одночленов считаются сами числа.

Пример. Одночлены

-7ab 3 , , -1x, 15

записаны в стандартном виде. Их коэффициенты соответственно равны числам -7, , -1, 15.

Коэффициент одночлена, равный 1 или -1 обычно не пишут.

Если одночлен имеет только буквенные множители, то условились считать, что его коэффициент равен +1 или -1, в зависимости от знака, который стоит (или подразумевается) перед одночленом.

Пример. Одночлены

записаны в стандартном виде. Коэффициент первого из них равен 1, второго -1, так как

a = 1 · a, -xy = -1 · xy.

Целый положительный коэффициент означает, сколько раз повторяется слагаемым буквенное выражение, перед которым он стоит.

3ab = (ab) · 3 = ab + ab + ab.

Дробный положительный коэффициент означает, какая часть берётся от буквенного выражения, к которому он относится.

Пример. В одночлене коэффициент означает, что от x 2 берётся , потому что , а умножить на значит взять от множимого.

Отрицательный коэффициент означает, что буквенное выражение, перед которым он стоит, умножается на абсолютную величину этого коэффициента и результат берётся с противоположным знаком.

-4mn = -4 · mn = -(mn + mn + mn + mn).

Приведение одночлена к стандартному виду

С одночленами удобнее работать, когда они записаны в стандартном виде. Любой одночлен можно привести к стандартному виду путём тождественных преобразований. Процесс таких преобразований называют приведением одночлена к стандартному виду.

Привести одночлен к стандартному виду — значит выполнить с ним такие тождественные преобразования, чтобы он принял стандартный вид.

Чтобы привести одночлен к стандартному виду надо:

Выполнить группировку числовых множителей (если их несколько), а также одинаковых буквенных множителей и их степеней.
Вычислить произведение числовых множителей и по свойству степеней с одинаковыми основаниями перемножить буквенные множители.
Поставить на первое место числовой множитель, а после него расположить буквенные множители в алфавитном порядке.

Пример 1. Запишите одночлен -2b(-3)x 3 4ab 2 x 2 в стандартном виде.

Используя переместительное и сочетательное свойства умножения, сгруппируем по отдельности числовые и одинаковые буквенные множители. В результате исходный одночлен примет вид:

((-2) · (-3) · 4) · (b · b 2 ) · (x 3 · x 2 ) · a.

Перемножаем числовые множители и степени с одинаковыми основаниями. Произведение числовых множителей равно 24. Произведение степеней b равно b · b 2 = b 3 . Произведение степеней x равно x 3 · x 2 = x 5 :

24 · b 3 · x 5 · a.

Записываем на первом месте числовой множитель, а после него располагаем буквенные множители в алфавитном порядке. В итоге получаем одночлен стандартного вида:

24ab 3 x 5 .

-2b(-3)x 3 4ab 2 x 2 = ((-2) · (-3) · 4) · (b · b 2 ) · (x 3 · x 2 ) · a = 24 · b 3 · x 5 · a = 24ab 3 x 5 .

Пример 2. Представить одночлен -2a 4 c0b в стандартном виде.

Среди своих множителей, данный одночлен имеет множитель 0, значит всё произведение в результате будет равно 0. Стандартный вид нулевого одночлена есть 0:

Для краткости в одночлене знаки умножения не пишут, а только подразумевают. Так что если вы видите запись $\fracamc$, то это значит $\frac \cdot a \cdot m\cdot c$.

Одночлен может состоять и из одного числа или переменной.

Например, $4$ или $x$ – тоже одночлены.

Стандартный вид одночлена

Для удобства одночлены принято преобразовывать в стандартный вид. Для этого:

Во-первых, числовой множитель пишут в самом начале, причем он должен быть равен произведению всех числовых множителей одночлена.

Например: $a2b4c$ - записан в нестандартном виде.
Преобразовываем к стандартному: $a2b4c=a·2·b·4·c=2·4·a·b·c=8abc$ . Готово. Теперь у нас коэффициент стоит первым, и он не $2$ и не $4$, а $8$.

Во-вторых, буквенные множители располагают в алфавитном порядке, при этом одинаковые объединяют, записывая их как степени.

Например: $7acaba$ – не стандартен.
Преобразовываем: $7acaba=7aaabc=7a^3 bc$. Готово.

Приведенным в стандартный вид считается одночлен, в котором выполняются оба вышеозначенных требования.

Пример: Привести одночлен $n5kk3ax$ к стандартному виду.
Решение: Преобразовываем: $n5kk3ax=n·5·k·k·3·a·x=5·3·a·k·k·n·x=15ak^2 nx$.

Пример: Привести одночлен $2x^2 (-3)x^3$ к стандартному виду.
Решение: Выполняем: $2x^2 (-3) x^3=2·x^2·(-3)·x^3=2·(-3)·x^2·x^3=-6x^5$.

Преобразование одночленов в стандартный вид упрощает работу с ними, например, так удобнее приводить подобные слагаемые .

Пример: Привести подобные слагаемые в многочлене : $ax3x-x5ax^2+x^3 a+4xax+x2xa7x$
Решение: На первый взгляд, в задании совсем не понятно, какие слагаемые подобны, а какие – нет. Однако давайте приведем их к стандартному виду:

$ax3x-x5ax^2+x^3 a+4xax+x2xa7x=$
$=3ax^2-5ax^3+ax^3+4ax^2+14ax^3=. $

Вот теперь гораздо нагляднее! Записываем подобные рядом и приводим их:

Степень одночлена

Степенью одночлена называют сумму показателей степени всех буквенных множителей (переменных), входящих в его состав.

Например, степень одночлена $3a^2 c^3$ равна пяти (так как $2+3=5$). А степень одночлена $b$ – единице, так как буквенный множитель $b$ имеет именно первую степень (согласно свойствам степеней $b=b^1$).

Также обратите внимание на то, что одночлен состоящий из одного только числа имеет нулевую степень. Например, степень одночлена $5$ – ноль. Почему так? Потому что, у него нет буквенных множителей. Можно сказать и по-другому - они есть, но стоят в нулевой степени, ведь $5x^0=5·1=5$.

В этом уроке мы повторим основные понятия, связанные с одночленами: вспомним, что называют одночленом, как приводить одночлены к стандартному виду. Поговорим о коэффициентах и степенях одночленов. Затем вспомним, какие одночлены являются подобными и выполним действия над ними.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Одночлен"

· вспомнить, что называют одночленом;

· вспомнить, как одночлены приводить к стандартному виду;

· поговорить о коэффициентах и степенях одночленов;

· вспомнить, какие одночлены являются подобными.

Для начала давайте вспомним, что же называют одночленом.

Определение.

Одночленом называется произведение чисел и степеней переменных с натуральными показателями.

Числа и степени переменных также считаются одночленами.

А вот число 0 (нуль) называется нулевым одночленом.

На экране записаны следующие выражения:

Давайте выберем какие из указанных выражений являются одночленами, а какие – нет. Будем поочерёдно рассматривать каждое выражение.

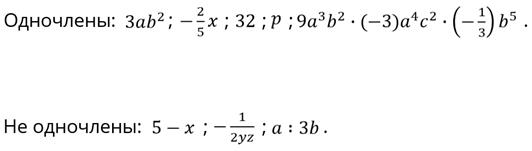
Обратите внимание, в последнем одночлене мы можем перемножить между собой числа и степени с одинаковыми основаниями. Следовательно, очень важную роль при работе с одночленами играют известные вам теоремы о степенях.

Вспомним их. Это умножение и деление степеней с одинаковыми основаниями, возведение в степень, а также умножение и деление степеней с одинаковыми показателями, но с разными основаниями.

Вернёмся к нашему последнему одночлену и упростим его.

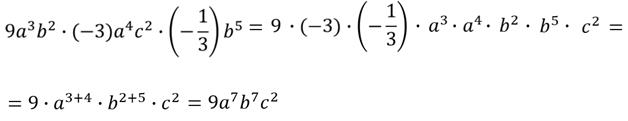
Такой вид одночлена называется стандартным.

Запомните, что в одночлене стандартного вида множители расположены в определённом порядке: на первом месте располагается числовой множитель, записанный цифрами, а за ним произведение степеней различных переменных.

При этом следует знать, что буквы в одночленах стандартного вида принято записывать в алфавитном порядке.

Кстати, любой одночлен можно привести к стандартному виду. Вспомним алгоритм приведения одночлена к стандартному виду.

Для того чтобы одночлен привести к стандартному виду нужно:

1) перемножить все числовые множители;

2) поставить полученный числовой множитель на первое место;

3) перемножить все степени, то есть получить буквенную часть.

Привести к стандартному виду одночлен: .

Решение: перемножим отдельно числовые множители и отдельно степени переменных. В результате получим,

Обратите внимание, что любое число представляет собой одночлен стандартного вида.

Среди одночленов: ; ; ; ; укажите одночлены стандартного вида.

Решение: первый одночлен хоть и представляет собой произведение, но заметим, что в нём дважды повторяется переменная b. А это говорит о том, что он не записан в стандартном виде.

Чего нельзя сказать о втором одночлене. Он является произведением числа и степени переменной. А значит, записан в стандартном виде.

Следующий одночлен представляет собой произведение числа и степеней переменных. Причём, все переменные записаны в алфавитном порядке. Следовательно, он записан в стандартном виде.

Четвёртый одночлен является произведением. Но заметим, числовой множитель не упрощён. Значит, данный одночлен не записан в стандартном виде.

И последний одночлен. Он представляет собой произведение числа и степеней переменных. Причём, все переменные записаны в алфавитном порядке. Следовательно, он записан в стандартном виде.

Определение.

Числовой множитель в одночлене стандартного вида называется коэффициентом одночлена.

В указанных нами одночленах стандартного вида коэффициенты равны 2, – 4,5 и 5,3.

Если коэффициент равен 𝟏, то он не пишется. Например,

Вернёмся к одночлену . И давайте найдём сумму степеней всех переменных в рассматриваемом одночлене. Ее нетрудно посчитать. Она равна 16. Напомним, такую сумму называют степенью одночлена.

Определение.

Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него.

Если одночлен является числом, отличным от нуля, то его степень считается равной нулю. Например, степень одночлена равна нулю. Степень одночлена также равна нулю.

Можно также сказать, что это одночлены нулевой степени. А вот степень нулевого одночлена не определена.

Найти степени одночленов: ; ; .

Решение: степень первого одночлена 5𝑥𝑦 равна 2, так как степени переменных 𝑥 и 𝑦 равны единице.

Степень второго одночлена равна:

Третий одночлен: является одночленом 16-ой степени, так как

Определение.

Одночлены, приведённые к стандартному виду, называются подобными, если они имеют одинаковую буквенную часть.

Подобные одночлены можно:

Сложение и вычитание подобных одночленов называется приведением подобных членов.

Перемножить или разделить два одночлена – это значит представить их произведение или частное в стандартном виде.

Возвести одночлен в степень – это значит представить эту степень в стандартном виде.

а) найти сумму: 4𝑥, 6𝑥, 𝑥;

б) найти разность: , ;

в) найти произведение: , ;

г) возвести во 2-ую степень: ;

д) найти частное: , .

Решение. В первом примере нужно найти сумму одночленов. Все эти три одночлена имеют стандартный вид и одинаковую буквенную часть. Следовательно, они подобны. И значит, можем найти их сумму. Для этого мы сложим их коэффициенты, а буквенную часть перепишем без изменений. Получим,

Таким образом, мы сложили три одночлена и в результате получили одночлен, который также представлен в стандартном виде.

Во втором примере нужно найти разность одночленов. Данные одночлены записаны в стандартном виде и подобны. Значит, можем найти их разность. Для этого мы вычтем коэффициенты, а буквенную часть перепишем без изменений. Получим,

В следующем примере найдём произведение одночленов. Это одночлены стандартного вида, так как у них на первом месте располагаются числовые множители, а за ними следуют степени переменных. Запишем произведение этих одночленов. Далее воспользуемся переместительным и сочетательным свойствами умножения. Затем перемножим числовые множители и выполним умножение степеней с одинаковыми основаниями. В результате получим,

Таким образом, мы умножили один одночлен на другой и в результате получили одночлен, который представили в стандартном виде.

В следующем примере нужно возвести одночлен во вторую степень. Воспользуемся правилом возведения в степень произведения и получим,

Таким образом, возведя одночлен в степень, мы также получили одночлен, причём стандартного вида.

И последний пример. Здесь нам нужно выполнить деление одночленов. Оба одночлена имеют стандартный вид. Для более удобного решения будем использовать черту дроби. Сначала разделим числовые коэффициенты. Затем разделим буквенные множители одночленов, опираясь на теорему о делении степеней. Получим,

Таким образом мы разделили один одночлен на другой и в результате снова получили одночлен стандартного вида.

Напомним, что не всегда при делении одночленов результатом будет одночлен. В случае, если делитель содержит переменные, которые присутствуют в делимом, причём некоторые или все соответствующие показатели степеней в делителе больше, чем в делимом, то результатом такого деления будет алгебраическая дробь.

Также алгебраическую дробь мы получим и в случае, если делитель содержит переменные, которые отсутствуют в делимом.

На этом уроке мы повторили основные понятия, связанные с одночленами. А именно, вспомнили, что одночленом называется произведение чисел и степеней переменных с натуральными показателями. Кстати, числа и степени переменных также считаются одночленами. А вот число нуль называется нулевым одночленом. Вспомнили, как одночлены приводить к стандартному виду. Поговорили о их коэффициентах и степенях одночленов. Затем вспомнили какие одночлены являются подобными и выполнили действия над ними.

Одночлен – одно из основополагающих понятий в алгебре. Данный урок поможет вам разобраться с его определением, а также со стандартным видом одночлена, степенью и коэффициентом.

Что такое одночлен

Оказывается, любые числа (положительные или отрицательные), любые переменные или их степени – это одночлены, к примеру: $8$ или $-92$ или $d^7$. И даже любые дроби $\frac$ или $0,3$ являются одночленами.

При этом переменные могут быть представлены любыми буквами ($z$, $m$, $j$, $v$, $a$ и т. п.). Любые числа без переменных (натуральные, дробные или целые, рациональные, действительные, в степени) называют одночленом без переменной.

Также выражения, представляющие собой произведение различных множителей, называют одночленами, например: $$2\times n^2$$

$$a\times 3\times 2x$$

$$-5,5y^\times 84b\times 302$$ То есть, в одночлен могут входить как несколько множителей, так и одно число или переменная.

Таким образом, запомним определение:

Числа, переменные, их степени с натуральным показателем, а также различные виды произведений, составленные из этих переменных, чисел и степеней, называют одночленами.

Какие же выражения не относятся к одночленам? Приведем примеры: $$s+f$$

$$\frac$$ Иными словами, выражения, содержащие сумму, разность или переменную в знаменателе дроби, одночленами являться не будут.

Стандартный вид одночлена

Для удобства математических вычислений одночлен принято приводить к стандартному виду. Разберемся, что это значит.

Стандартный вид одночлена подразумевает его запись с соблюдением нескольких правил:

Если в выражении среди других множителей есть одночлен без переменной (числовой множитель), то он всегда записывается первым. Это число называют коэффициентом одночлена. Стандартным видом одночлена $c^4\times 74$, к примеру, будет $74$, а $74$ – его коэффициент.

Если в одночлене несколько числовых множителей без переменных, то впереди записывают их произведение. Полученное число также будет являться коэффициентом. Например, приведем к стандартному виду одночлен $21\times k^3\times 4$. Умножим $21$ на $4$ и запишем получившийся коэффициент первым: $$84k^3$$

В случае, если среди множителей есть несколько степеней с одинаковой переменной, то также вычисляют их произведение, например: $$c\times c^4\times s^2\times c^3$$ Стандартный вид: $$c^8\times s^2$$ То есть мы сложили все показатели натуральных степеней переменной $c$.
Таким же образом необходимо перемножить все степени с другими буквенными основаниями. В конечном итоге необходимо расположить получившиеся степени переменных в алфавитном порядке. Например, выражение $6f\times 7d\times \times 3f^3$ запишем в стандартном виде и получим: $$126$$

Коэффициент

Коэффициентом одночлена называют числовой множитель одночлена, который записан в стандартном виде.

В случаях, когда коэффициент в результате вычислений оказался равен $1$, он обычно не записывается, но подразумевают, что он есть. Если коэффициент получился равным $-1$, то в стандартном виде минус без единицы записывают в самом начале.

Заметим, что после тождественных преобразований можно привести к стандартному виду абсолютно любой одночлен.

Пример

Запишем в стандартном виде выражение: $\frac \times >\times m^\times c^\times 0,25\times $.

При умножении числовых множителей сначала преобразуем десятичную дробь $0,25$ в простую и получим $\frac $. Тогда стандартный вид этого одночлена будет: $$\frac \times c^\times >\times m^$$

Степень одночлена

Вместе с понятием одночлена изучают его степень, которая представляет собой сумму показателей всех степеней входящих в него переменных. То есть, если необходимо будет, например, посчитать степень одночлена $5h^3\times f^\times 3v$, мы получим: $$3+18+1=22$$ В данном случае, степень переменной $v$ равна единице.

Таким образом, запомним:

Степенью одночлена, записанного в стандартном виде, будет сумма показателей степеней всех переменных, которые в него входят.

Если же в одночлене переменных нет, то его степень будет равна $0$. При этом сам он должен быть отличным от нуля. К примеру, степень одночлена $57$ равна $0$. Если одночлен равен $0$, то его называют одночленом с неопределенной степенью.

Читайте также: