Как сделать мандельброт

Добавил пользователь Евгений Кузнецов
Обновлено: 05.10.2024

В этой статье приведены примеры расчета и построения графической интерпретации некоторых алгебраических и геометрических фракталов.

Фракталы можно разделить на несколько видов:

Геометрические фракталы – строятся на основе исходной фигуры (линии, многоугольника или многогранника) путем ее дробления и выполнения различных преобразований полученных фрагментов.
Алгебраические фракталы – строятся на основе алгебраических формул.
Стохастические фракталы – получаются, если в итерационном процессе случайным образом изменять какие-либо параметры.

Фракталы нашли применение в физике (моделирование сложных процессов и материалов), биологии (моделирование популяций, описание сложных ветвящихся структур), технике (фрактальные антенны), экономике. Существуют алгоритмы сжатия изображений с помощью фракталов. В компьютерной графике фракталы используются для построения изображений природных объектов – растений, ландшафтов, поверхности морей и т. д.

Некоторые примеры алгебраических и геометрических фракталов

Фрактал Мандельброта

Рассмотрим последовательность комплексных чисел:

\[z_ = z_k^2 + c, k = 0, 1, 2, \dots, z_0 = c\]

Множество точек c, для которого эта последовательность не расходится, называется множеством Мандельброта. Для построения его графической интерпретации нужно определить исходные данные:

прямоугольное окно C с разрешением $m \times n$ точек;
значение $r_ = 2$ – минимальный радиус расходимости множества Мандельброта
максимальное число итераций $k_\max$

Если точка $z_k$ вышла за пределы круга радиуса $r_\min$ при $k \lt k_\max$, то процесс вычисления останавливается.

Построение: для каждой точки $c_ \in C (i = \overline, j = \overline, c_x \in [-2; 1], c_y \in [-2; 1,5])$ запустим итерационный процесс:

\[x_ = x_k^2 - y_k^2 + c_x, x_0 = c_x\] \[y_ = 2 x_k y_k + c_y, y_0 = c_y\]

где $k = 0, 1, 2, \dots, k_\max$ и $\sqrt \leqslant r_\min$.

Составим матрицу M , элементы которой $m_ \in [1; k_\max]$ равны номерам итераций, на которых процесс был остановлен. Далее матрицу можно вывести на экран как растровое изображение, предварительно сопоставив каждому числу из интервала $[1, k_\max]$ некоторый цвет.

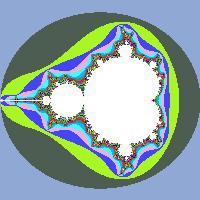
Если представить множество в общем виде:

то, изменяя значение N, можно получать симметричные фрактальные множества. Например, для $N = 4$ и $N = 7$:

Фрактал Жюлиа

Рассмотрим ту же последовательность комплексных чисел, что и для множества Мандельброта:

\[z_ = z_k^2 + c, k = 0, 1, 2, \dots\]

Исходные данные, этапы построения и условия остановки – те же, что и для фрактала Мандельброта, за исключением:

значение c фиксируется: $c = 0,36 + 0,36i$
начальное значение $z_0$ перебирается дискретно в области $C \in [-1;1] + [-1;1]i$

Рассматривая множество в общем виде: $z_ = z_k^N + c$ и изменяя N и с, можно получать разнообразные фрактальные множества:

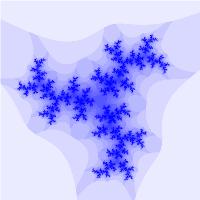
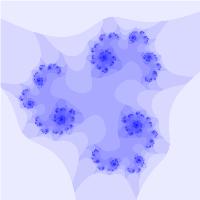
Бассейны Ньютона

Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости.

Общая формула метода Ньютона имеет вид:

При выборе различных $z_0$ процесс будет сходиться к различным корням (областям притяжения). Границы этих областей имеют фрактальную структуру.

Подставив $p(z)$ в формулу метода, получим итерационную формулу для построения фрактала:

Итерационный процесс останавливается при:

\[\left| z_^3 \right| \leqslant r_\min\]

Для построения графической интерпретации также как и для фрактала Мандельброта, используется матрица, элементы которой равны номеру итерации, на которой остановился процесс.

Если записать формулу в общем виде:

\[p(z) = z^N - 1\] \[\left| z_^N - 1 \right| \leqslant r_\min\]

то можно получить изображения фракталов более сложной формы:

L-системы

В 1968 году венгерский биолог Аристид Линденмайер предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена для моделирования сложных ветвящихся структур (разнообразных растений). Эта модель получила название Lindenmayer System (Система Линденмайера или L-система).

Рекурсивная природа L-систем позволяет строить с их помощью геометрические фрактальные изображения.

L-система определяется как $G = (V, \omega, P)$ , где

V - алфавит – множество символов, содержащее элементы, которые могут быть замещены (переменные).
ω – строка символов из множества V, определяющая начальное состояние системы (аксиома).
P – набор правил, определяющий, как переменные могут быть замещены другими переменными и константами.

Правила применяются итеративно, начиная с аксиомы. За одну итерацию применяются одновременно все правила.

Например, L-система имеет вид:

Правила: $(A \rightarrow AB) (B \rightarrow BA)$

После нескольких применений правил из аксиомы получаются строки:

Пример некоторых фракталов, построенных с помощью L-систем - кривая дракона и растение:

Лист папоротника

Существует несколько способов построения этого фрактала.

1) Построение с помощью системы итерируемых функций (IFS)

Производится 20 итераций функции $f(x, y)$. Каждое новое значение получается из предыдущего в зависимости от случайного числа, т. е. вычисляется с использованием таблицы распределения:

Вероятность	$$x'$$	$$y'$$
0,01	$$0$$	$$0,16y$$
0,85	$$0,85x + 0,04y$$	$$-0,04x + 0,85y + 1,6$$
0,07	$$0,20x - 0,26y$$	$$0,23x + 0,22y + 1,6$$
0,07	$$-0,15x + 0,28y$$	$$0,26x + 0,24y + 0,44$$

После выполнения всех итераций точка рисуется на экране.

Начальные значения x и y могут быть константами (желательно не большими, чем 1) или их можно выбирать случайным образом на отрезке $[0;1]$.

2) Рекурсивное построение

Для построения используется процедура (псевдокод):

$R(\phi) = \begin \cos(\phi) && \sin(\phi) \\ -\sin(\phi) && \cos(\phi) \end$ - матрица поворота на угол φ.

$p_0 = [x_0; y_0]$ - координаты начальной точки
h – высота листа
ψ – угол отклонения листа от вертикали
side – направление изгиба ветви
δ – минимальная длина ветви ветвящегося отрезка
rec – максимальная глубина рекурсии

Рекомендуемые значения углов и коэффициентов: $\phi_0 = 14,9^, \phi_1 = 37,7^, \phi_2 = 36,8^, \phi_3 = 17,6^, k_1 = 0,0483, k_2 = 0,162, m_1 = 0,371, m_2 = 0,336, m_3 = 0,849$.

Для получения более реалистичного изображения можно использовать метод управляемой случайности. Метод заключается в том, что в процесс сознательно вносятся помехи. В алгоритме построения ветви папоротника можно внести изменения в углы ветвления φ1, φ2, φ3.

Например, если ввести случайные воздействия на углы помех, равномерно распределенных на интервале $(-10^; 10^)$, можно получить изображения:

Литература:

Программы

Здесь приведены ссылки на программы, с помощью которых были созданы иллюстрации для этой статьи.

Python, Cython рисуют чудесный набор Мандельброта, набор фракталов Мандельброта

В 1960-х и 1970-х годах американский математик Бенуа Б. Мандельброт практически единолично основал новый раздел математики, а именно фрактальную геометрию. Эта новая отрасль математики помогает людям исследовать математические законы, лежащие в основе физических явлений. Вихрь фрактального хаоса пронизывает математику, физику, химию, биологию, атмосферу, океан и даже социальные темы, а также оказал определенное влияние на области музыки и искусства.

Фрактальное искусство - фрактальное искусство отличается от обычной компьютерной живописи. Оно использует фрактальную геометрию и мощные вычислительные мощности компьютеров для итеративного вычисления математических формул в сочетании с эстетическим и художественным моделированием автора, превращая абстрактные и загадочные математические формулы в Произведения изысканной художественной росписи.

Уведомление об авторских правах

Эта статьяжестяная банкаСвободно воспроизводится в Интернете, но необходимо: указать источник (Автор: Сухарь, дядя) и содержать ссылку на эту страницу.

Эта статьяне можетАдаптировано и выдержано для публикации в статье.

1. Множество Мандельброта

1.1 Определение

1.2 Расчет

Очевидно, что компьютер не может выполнять бесконечные вычисления, чтобы подтвердить, расходится ли итеративное значение z, вызванное c, поэтому мы просто вычисляем время выхода точки c, то есть сколько раундов итерационных вычислений, модуль значения z превышает 2. В процессе рисования время ухода будет цветом точки c на плоскости.

Как показано в коде, abs (z) используется для вычисления модуля комплексного числа.В этом коде максимальное время выхода составляет 100-1 = 99. В то же время следует отметить, что Python изначально поддерживает операции с комплексными числами, z * z + c - это операция между комплексными числами, а его код не отличается от обычных действительных чисел.

Далее вы можете рассчитать множество Мандельброта. Обобщенное множество Мандельброта представляет собой бесконечную комплексную плоскость, и мы, очевидно, можем нарисовать только ее небольшой фрагмент. Следующий код вычисляет набор Мандельброта в квадратной области с (xCenter, yCenter) в качестве центральной точки и semiWidth в качестве полуширины. Диапазон координат x этой квадратной области равен xCenter ± semiWidth, а диапазон координат y равен yCenter ± semiWidth. Учитывая, что компьютер может вычислять только дискретные точки, квадратная область будет разделена на N * N точек для расчета. Когда N = 600, матрица результатов следующей функции представляет собой изображение 600x600, а значение прямоугольного элемента представляет цвет точки.

Разобраться в приведенном выше коде непросто, вам нужно начать с операции трансляции многомерных данных np.ndarray. В сложных проблемах может помочь мелкомасштабное моделирование.

Np.ogrid - это специальный объект, который использует кортежи срезов в качестве индексов, особенно для создания массивов для широковещательной передачи. 1: 4: 4j чем-то похож на np.linspace (1,4,4), используемый для генерации арифметической последовательности из 4 элементов от 1 до 4 (включая 4), где j не означает комплексное число, а просто Вид выражения. Можно видеть, что y, сгенерированный ogrid, представляет собой двумерный массив с 4 строками и 1 столбцом, а x - двумерный массив с 1 строкой и 3 столбцами. Его стоимость см. Выше.

Y * 1j умножает комплексное число 1j на каждый элемент y и возвращает массив той же формы (размерности). Поскольку модуль numpy не является собственным содержимым Python, знак * здесь не является обычным умножением Python. На самом деле это перегруженная операторная функция. Эта функция находится в модуле numpy и написана на языке C. Можно видеть, что действительная часть результирующего элемента y * 1j равна 0, а мнимая часть равна исходному значению элемента, умноженному на 1j.

Давайте посмотрим, что получит x + z. Обратите внимание, что z здесь является результатом y * 1j.

Обратите внимание на комплексное число в массиве c еще раз и рассматривайте его как изображение. Сверху вниз значение мнимой части увеличивается в арифметике; слева направо значение действительной части увеличивается в арифметике.

Теперь эту программу легко понять. Она использует тот же метод, что и описанный выше процесс интерпретации, чтобы разделить сложную квадратную область с (xCenter, yCenter) в качестве центральной точки и полуширины в качестве радиуса на N строк и N столбцов, а также размеры многомерного массива c То есть (N, N). Элементы в c являются комплексными числами, и их действительные части изменяются по горизонтали от xFrom до xTo, а их мнимые части меняются по вертикали от yFrom до yTo.

Посмотрим на последнюю строчку кода функции:

GetEscapeTime © - это функция языка Python, которая была определена ранее. Она принимает комплексный параметр c, вычисляет и возвращает время перехода, соответствующее этому сложному параметру. Функция np.frompyfunc () передает комплексные элементы в двумерном массиве c один за другим в getEscapeTime () для вычисления и получает массив результатов с той же формой, что и c. Сколько элементов в c, сколько раз будет выполняться функция getEscapeTime (). Выполните функцию astype массива результатов, чтобы преобразовать все элементы в массиве результатов в тип np.float. Приведенный выше параметр 1,1 означает, что функция getEscapeTime () принимает 1 параметр и возвращает 1 элемент результата.

Таким образом, функция computeMandelbrot () наконец возвращает двумерный массив с N строками и N столбцами. Элементы массива относятся к типу np.float, что указывает время выхода точки; а номер строки и столбца, в которых расположен элемент, косвенно указывает, что точка элемента находится в Изображение результата / координаты в комплексной плоскости.

1.3 Рисунок

Мы использовали matplotlib для рисования части множества Мандельброта. Центральная точка левого изображения - c = 0,27322626 + 0,595153338j, полуширина квадрата - 0,2; центральная точка правого изображения такая же, как и у левого изображения, а полуширина - 0,2. 3 , Что эквивалентно увеличению левого изображения в 25 раз.

Затем проанализируйте код.

Фигура в pyplot называется фигурой, и фигура содержит одну или несколько подфигурных осей. Функция drawMandelbrot () отвечает за вычисление и отрисовку изображения множества Мандельброта на подграфе. ax.set_axis_off () скрывает координаты фрагмента изображения, а затем вычисляет массив результирующего изображения ds из N * N пикселей, а затем использует функцию ax.imshow () для рисования ds на фрагменте изображения. Эта функция обрабатывает двумерные данные ds как двумерное изображение, и каждый элемент в ds соответствует пикселю изображения. Функция cmap в функции imshow () соответствует объекту сопоставления цветов, который отвечает за преобразование значения элемента (то есть времени перехода комплексного числа c) в соответствующий цвет.

Функция refresh () дважды вызывает функцию drawMandelbrot (), чтобы нарисовать левый подграф-ax0 и правый подграф-ax1. Обратите внимание, что координаты центральной точки на двух рисунках одинаковы, разница в том, что полуширина разная: одна - 0,2, другая - 0,2. 3 , Cm в matplotlib отвечает за управление объектами сопоставления цветов.Функция cm.get_cmap () может использоваться для получения соответствующих объектов сопоставления цветов через строковые имена, такие как 'радуга'. Функция para.fig.canvas.draw () информирует рисунок / fig о необходимости перерисовки. Здесь мы видим объект с именем para, и следующий код объясняет это.

Функция plt.figure () создает фигуру-фигуру длиной 12 дюймов и шириной 6 дюймов. Обратите внимание, что для параметра dpi / точек на дюйм установлено значение 100, что означает, что размер фигуры составляет 1200 пикселей в длину и 600 пикселей в ширину.

Функция plt.subplots_adjust () регулирует интервал и поля между подзаголовками, полностью используя все окно отображения.

Plt.subplot (121) создает подграф-оси в текущем объекте фигура-фигура и сохраняет его в para.ax0. Параметр 121 обрабатывается этой функцией особым образом, что означает, что видимая область текущей фигуры делится на 1 Строки и 2 столбца. Создайте подграф в позиции 1, которая является левым подграфом в результате. Таким же образом plt.subplot (122) делит видимую область текущего графика на 1 строку и 2 столбца и создает подзаголовок в позиции 2, который является правым подзаголовком в результате.

Функция refresh () вычислит и отрисует два подграфа. plt.show () отображает окно.

Далее, давайте изучим функцию перехвата on_key_release (event). Эта функция позволяет оператору нажимать стрелки вверх и вниз для изменения цвета текущего изображения и перерисовки. Список para.cmaps хранит имена ряда доступных объектов отображения, а para.idxColorMap записывает индексы используемых в данный момент объектов отображения в списке para.cmaps. Функция on_key_release (event) определяет тип ключа, соответствующий событию, если он активен, para.idxColorMap + 1, если он не работает, para.idxColorMap-1. Функция on_key_release () реализует перерисовку графика путем вызова функции refresh (). Внутри функции обновления para.idxColorMap используется после взятия модуля len (para.cmaps). Это связано с тем, что добавление и вычитание para.idxColorMap не проверяется на выход за пределы. Para.idxColorMap может быть отрицательным числом или положительным числом, превышающим длину para.cmaps. Modulo может гарантировать получение правильного подстрочного индекса.

Напоминаем читателю, что одно дополнительное изображение имеет 600 * 600 = 360 000 пикселей, а два дополнительных изображения - 720 000 пикселей. Функция getEscapeTime () вызывается один раз для расчета каждого пикселя, и эта функция написана на языке Python, и в ней не более 100 операций цикла, а скорость выполнения очень низкая. Поэтому после того, как средство чтения выскочит из интерфейса, не слишком беспокойтесь, нажимая стрелки вверх и вниз, и нажмите их снова после завершения обновления.

2. Cython ускоряет набор Мандельброта.

Программа рисования множеств Мандельброта, написанная на чистом Python, слишком медленная! Но Python - это так называемый связующий язык, который может легко писать библиотеки расширений на C или других языках. Numpy, scipy, matploblib - все это выдающиеся представители этих библиотек расширений.

Есть как минимум два способа ускорить вычисление множеств Мандельброта. Метод 1 состоит в том, чтобы напрямую написать функцию для вычисления времени перехода на языке C, затем использовать компилятор mingw, g ++ или Visual C ++ для компиляции ее в целевой модуль, а затем вызвать ее на языке Python. Это очень хлопотно, потому что параметры функции нужно анализировать вручную, а также нужно запоминать и использовать множество API-интерфейсов Python.

Метод 2 - Cython. Cython в основном такой же, как Python с точки зрения синтаксиса, и в то же время позволяет напрямую определять и вызывать функции языка C и определять типы переменных. Компилятор Cython компилирует исходные программы Cython в программы на языке C, а затем компилирует их в модули Python с помощью компилятора языка C. Поскольку сам интерпретатор Python написан на языке C и скомпилирован компилятором языка C, легко получить доступ к объектам типа Python в Cython.

2.1 Подготовка окружающей среды

Если читатель использует Linux, обычно достаточно компилятора gcc, поставляемого с системой. Процесс компиляции кода Cython под Linux эквивалентен следующему процессу, но детали могут отличаться.

Читателям также необходимо установить модуль Cython, запустить pip install cython в командной строке Windows или в терминале Linux.

2.2 Перепишите функцию вычисления времени ухода

Создайте новый файл (New-> File) в PyCharm и назовите его MandelbrotComp.pyx. Внутри находится код Cython:

Как видите, приведенный выше код в основном отличается от функции getEscapeTime (), написанной ранее на чистом Python:

Прежде всего, все переменные / объекты имеют объявления типов, большинство из которых определяется ключевым словом cdef. Тип c и z сложный, а тип i - int. Строгая типизация - это характеристика C / C ++, а также необходимое условие для C / C ++ компиляции эффективного машинного кода.

Во-вторых, мы больше не используем abs для вычисления модуля комплексного числа z. Это может быть вызвано двумя причинами: 1). Исходный язык C не имеет функции abs () для модуля комплексного числа, и использование abs () может вызвать Этот модуль снова вызывает внутреннюю функцию Python abs (); 2) Модульная операция над комплексными числами требует извлечения квадратных корней, а вычисление квадратных корней обходится дорого. Более того, здесь нет необходимости в решении квадратного корня. Мы непосредственно вычисляем сумму квадратов действительной и мнимой частей z и сравниваем, больше ли она 4, что фактически эквивалентно проверке того, больше ли модуль z 2.

2.3 Скомпилировать как модуль расширения

Согласно документации Cython, мы подготовили файл setup.py следующего содержания:

Другой сгенерированный файл называется MandelbrotComp.cp37-win_amd64.pyd. Если версия Python или операционная система читателя отличается от авторской, имя может быть другим. Этот файл представляет собой скомпилированный модуль расширения Python.

2.4 Вызов модуля расширения

Следует отметить, что если программа чтения не использует Windows, InteractiveMandelbrot.py нельзя запустить напрямую. Результат компиляции языка C связан с аппаратной платформой (архитектура Intel x86 или ARM), операционной системой и т. Д. Машинный код, скомпилированный под Windows, не может быть запущен непосредственно под Linux. Читателям необходимо перекомпилировать файл MandelbrotComp.pyx как модуль расширения.

2.5 Интерактивный рисунок Мандельброта

Вместе с книгой автор предоставил файл InteractiveMandelbrot.py, программа для рисования предоставляет интерактивные функции. Помимо использования стрелок вверх и вниз для изменения цвета рисунка, оператор также может использовать левую и правую кнопки мыши для увеличения / уменьшения изображения. Нажмите Esc, чтобы восстановить изображение.

Для достижения вышеуказанных функций автор добавляет figWidth, figHeight к объекту para, чтобы представить ширину и высоту окна рисования в пикселях. para.semiWidth указывает текущую полуширину чертежа. Когда полуширина рисунка становится меньше, это эквивалентно увеличению изображения.

Когда кнопка мыши отпускается, вызывается функция перехвата on_button_release ().

Эта функция сначала пересчитывает новые центральные точки рисования para.x, para.y с помощью para.figWidth, figHeight, координат щелчка мыши event.xdata, event.ydata и другой информации.

Если выскакивает левая кнопка мыши (event.button == 1), уменьшите половину ширины рисунка para.semiWidth и увеличьте изображение. В противном случае увеличьте полуширину рисунка и уменьшите изображение. За перерисовку отвечает функция refresh (). Центральная точка и половина ширины рисунка берутся из para.x, para.y и para.semiWidth.

"В принципе (множество Мандельброта) могло быть открыто сразу же, как только человек научился считать. Но даже если бы люди работали без устали и никогда не ошибались, всех представителей человеческого рода, живших когда-либо на Земле, не хватило бы, чтобы выполнить элементарные арифметические действия, необходимые для построерия множества Мандельброта умеренного размера" английский писатель, учёный, футуролог Артур Кларк

". есть простые множества математических правил, которые, когда их прослеживает компьютер, порождают очень сложные образцы, которые никогда не повторяют себя полностью. Окружающий нас мир тоже включает в себя огромное количество сложных образцов, которые никогда полностью не повторяют себя. Вывод: в основе многих исключительно сложных явлений мира лежат простые правила. При помощи мощных компьютеров исследователи, занимающиеся хаососложностью, могут эти правила определить" американский публицист Джон Хорган

Множество названо в честь Бенуа Мандельбро.

Фрактал (лат. fractus — дроблёный, сломанный, разбитый) — множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей). В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную от топологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев. Википедия

Мандельбред, или Мандельброт (или Мандельбрей, как я знал это в детстве), - это восточноевропейское и русское еврейское дважды выпеченное печенье. В некотором смысле он похож на своего двоюродного брата Бискотти, знаменитого итальянского печеного печенья, дважды сдобного, но Мандельброт богат на яйца и жир и превращается в более мягкое, более нежное печенье с жареной наружной поверхностью, которая также сочетается с горячим чаем, как Бискотти делает с эспрессо.

Хотя у меня есть некоторая эмоциональная привязанность к Мандельброту (которую моя двоюродная бабушка делала круглый год), настоящая причина, по которой Мандельброт остается одним из моих любимых печенек, заключается в том, что текстура очень привлекательна. После нарезки второй пирог становится более жарким, чем нарезанный. С первого же запекания он хрустящий по краям, и даже после всей выпечки его все равно легко кусать (я смотрю на тебя, ломающий зуб бискотти). Кроме того, он выдерживает до комнатной температуры до шести дней, что делает его отличным выпечкой по выходным и готовым во время курортного сезона для перерывов на чай, кофе-бранчей, а также для удовольствия, когда друзья или члены семьи останавливаются,

Испеки Мандельброта дважды для хрустящего, нежного печенья

Мандельброт - это печенье, которое выпекается в форме бревна в первый раз, пока не будет готово примерно на 95 процентов, затем охлаждается на противне до тех пор, пока оно едва нагревается на ощупь, а затем нарезается и снова запекается. Внешняя сторона должна быть светло-карамельно-коричневой и четкой, а центр, хотя и прощающий под острым зубчатым ножом, совсем не грубый или мягкий.

Так же, как и Бискотти, первый пирог является ключевым. Если он не запечен в первый раз, ваш Мандельброт никогда не поджарится должным образом. Если в первый раз он получится слишком жареным, единственной проблемой будет то, что при резке манделброт будет немного крошиться по краям. Не волнуйтесь вообще - это простоватый, домашний рецепт, и у большинства Мандельброта есть кое-где сломанные края.

Как настроить Мандельброта

В этом рецепте много разных видов орехов работают очень хорошо, в том числе миндаль с ломтиками, лесные орехи с кожурой и орехи макадамия. Кстати, когда дело доходит до добавления орехов, я очень верю в то, что нужно время, чтобы жарить орехи, чтобы добавить богатство и глубину, пробуждая все эти летучие ореховые масла. Вы также можете заменить любые сухофрукты или любую цитрусовую цедру теми, которые используются здесь. Мне нравится мой Мандельброт с жареными нарезанными лесными орехами или миндалем и курагой или сушеным инжиром.

Измените дополнения, а не тесто: поскольку в тесте есть коричневый сахар, что довольно необычно для Мандельброта, я бы не стал играть ни с чем (например, с мукой), кроме надстроек, иначе печенье может легко испечь слишком мягкий или слишком жесткий.

Призрачный Мандельброт

Этот рецепт имеет много возможностей заранее. Тесто может быть охлаждено до одного дня до выпечки. При первом выпекании приготовление может занять несколько минут, от 42 до 47 минут. После того, как бревна теста обернуты в пластик, они также могут быть хорошо завернуты в фольгу и заморожены на месяц. Они будут чуть более сухими, чем если бы их запекли сразу после быстрого охлаждения. Разморозить в холодильнике и выпекать, как указано.

Смешайте сухие ингредиенты: просейте муку, соль, разрыхлитель, пищевую соду, корицу и мускатный орех в миске; отложить в сторону. (Образ

Смешайте сахар, яйца и приправы: Поместите сахар-песок, коричневый сахар, яйца, масло или масло, ваниль и апельсиновую цедру в миску миксера, снабженного насадкой для лопастей. (В качестве альтернативы используйте электрический ручной миксер и большую миску.) Смешайте на средней-низкой скорости до полного смешивания и слегка пенистой, около 3 минут. (Образ

Добавьте несколько сухих ингредиентов: добавьте около двух третей смеси муки к яичной смеси и перемешайте с низкой скоростью до полного смешивания. (Образ

Мука из клюквы и грецких орехов: добавьте клюкву и грецкие орехи в оставшуюся смесь муки и аккуратно перемешайте до получения хорошего покрытия. (Образ

Добавить фрукты и мучную смесь: добавить муку и фруктовую смесь к яичной смеси и перемешивать с низкой скоростью до однородного состояния. (Образ

Сформируйте тесто и остудите: разорвите один большой кусок полиэтиленовой пленки и положите на рабочую поверхность. Выкопайте половину теста в центр и сформируйте в бревно размером 12 на 1 1/2 дюйма, высота которого составляет 1 3/4 дюйма. Заверните полностью в полиэтиленовую пленку. Повторите с оставшимся тестом. Охладите до полного охлаждения, около 30 минут. (Образ

Подготовка к выпеканию: за 15 минут до того, как вынуть тесто из холодильника, подготовьте 2 стойки, чтобы разделить духовку на три части и нагрейте до 350 ° F. Распылите 2 разбитых противня с разбрызгивателем и выровняйте их пергаментной бумагой; отложить в сторону. (Образ

Частично охладите бревна: дайте остыть в течение 15-20 минут на противне. (Образ

Разрежьте бревна на печенье: перенесите бревна на чистую сухую разделочную доску. Используя длинный острый зубчатый нож, аккуратно нарежьте каждое бревно по диагонали на ломтики толщиной 1/2 дюйма. У вас будет около 24 файлов cookie из каждого журнала. Используя плоский шпатель, аккуратно перенесите каждую сторону среза обратно на противни, равномерно распределив их. (Образ

Выпекайте печенье снова: Выпекайте снова до тех пор, пока печенье не поджарится, края среза имеют легкую золотую корочку, и они становятся слегка твердыми на ощупь в центре, 12-15 минут. Осторожно перенесите печенье в охлаждающую подставку и полностью остудите. (Образ

Читайте также: