Как сделать круг под углом

Обновлено: 04.07.2024

\u041a \u0441\u043e\u0436\u0430\u043b\u0435\u043d\u0438\u044e, \u0432 \u0437\u0430\u0434\u0430\u043d\u0438\u0438 \u043d\u0435 \u0441\u043a\u0430\u0437\u0430\u043d\u043e, \u043a\u0430\u043a \u0440\u0430\u0441\u043f\u043e\u043b\u043e\u0436\u0435\u043d \u044d\u0442\u043e\u0442 \u0443\u0433\u043e\u043b.

\u0414\u0430\u044e 2 \u0432\u0430\u0440\u0438\u0430\u043d\u0442\u0430:

- 1) \u043a\u0440\u0443\u0433 \u0432 \u043f\u043b\u043e\u0441\u043a\u043e\u0441\u0442\u0438 \u043f\u043e\u0434 \u0443\u0433\u043b\u043e\u043c 30\u00b0 \u043a \u043a\u043e\u043e\u0440\u0434\u0438\u043d\u0430\u0442\u043d\u043e\u0439 \u043f\u043b\u043e\u0441\u043a\u043e\u0441\u0442\u0438 \u0425\u041e\u0423.

\u0422\u043e\u0433\u0434\u0430 \u0435\u0433\u043e \u0434\u0438\u0430\u043c\u0435\u0442\u0440 \u0432 \u043f\u043b\u043e\u0441\u043a\u043e\u0441\u0442\u0438 YOZ \u0432\u0438\u0434\u0435\u043d \u0441 \u0440\u0430\u0437\u043c\u0435\u0440\u043e\u043c 0,5*sin 30\u00b0 = 0.25 \u0441\u043c. \u041f\u043e\u043b\u0443\u0447\u0435\u043d\u043d\u044b\u0439 \u044d\u043b\u043b\u0438\u043f\u0441 \u0441\u0442\u0440\u043e\u0438\u0442\u0441\u044f \u043f\u043e \u043a\u043e\u043e\u0440\u0434\u0438\u043d\u0430\u0442\u0430\u043c \u0442\u043e\u0447\u0435\u043a \u043f\u043e \u0444\u043e\u0440\u043c\u0443\u043b\u0435: \u0443 = +-(\u221a(0,25 - 4\u0445\u00b2))\/2.

- 2) \u043a\u0440\u0443\u0433 \u0432 \u043f\u043b\u043e\u0441\u043a\u043e\u0441\u0442\u0438 \u043f\u043e\u0434 \u0443\u0433\u043b\u043e\u043c 30\u00b0 \u043a \u043a\u043e\u043e\u0440\u0434\u0438\u043d\u0430\u0442\u043d\u043e\u0439 \u043f\u043b\u043e\u0441\u043a\u043e\u0441\u0442\u0438 YOZ.

\u0422\u043e\u0433\u0434\u0430 \u0435\u0433\u043e \u0434\u0438\u0430\u043c\u0435\u0442\u0440 \u0432 \u043f\u043b\u043e\u0441\u043a\u043e\u0441\u0442\u0438 YOZ \u0432\u0438\u0434\u0435\u043d \u0441 \u0440\u0430\u0437\u043c\u0435\u0440\u043e\u043c 0,5*sin (90-30)\u00b0 = 0.433013 \u0441\u043c. \u041f\u043e\u043b\u0443\u0447\u0435\u043d\u043d\u044b\u0439 \u044d\u043b\u043b\u0438\u043f\u0441 \u0441\u0442\u0440\u043e\u0438\u0442\u0441\u044f \u043f\u043e \u043a\u043e\u043e\u0440\u0434\u0438\u043d\u0430\u0442\u0430\u043c \u0442\u043e\u0447\u0435\u043a \u043f\u043e \u0444\u043e\u0440\u043c\u0443\u043b\u0435: \u0443 = +-(\u221a(0,75 - 3\u0445\u00b2))\/2. ">]" data-testid="answer_box_list">

В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.

Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Ниже будут рассмотрены основные типы сопряжений.

Сопряжение углов (Сопряжение пересекающихся прямых)

Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)

В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)

Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.

Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Сопряжение параллельных прямых линий

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Сопряжение окружностей(дуг) с прямой линией

Внешнее сопряжение дуги и прямой линии

В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.

Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности O R радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой О r .

Из центра сопряжения, точки О r , опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности О R и центр сопряжения О r линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Внутреннее сопряжение прямой линии с дугой

По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности O R радиусом R-r. Точка О r , полученная на пересечении прямой и дуги, и будет центром сопряжения.

Из центра сопряжения(точка О r ) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.

Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности О R прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки О r , центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Смешанное сопряжение дуг окружностей

Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Овал – это замкнутая выпуклая плоская кривая. Самым простым примером овала является окружность. Начертить окружность не составляет труда, построить овал же можно при помощи циркуля и линейки.

- циркуль;
- линейка;
- карандаш.

Пусть нам известна ширина овала, т.е. его горизонтальная ось. Построим отрезок AB, разный горизонтальной оси. Разделим этот отрезок на три равные части точками C и D.

Из точек C и D как из центров построим окружности радиусом, равным расстоянию между точками C и D. Точки пересечения окружностей обозначим буквами E и F.

Соединим точки C и F, D и F, C и E, D и E. Эти прямые пересекают окружности в четырех точках. Назовем эти точки G, H, I, J соответственно.

Заметим, что расстояния EI, EJ, FG, FH равны. Обозначим это расстояние как R. Из точки E как из центра проведем дугу радиусом R, соединяя точки I и J. Соединим точки G и H дугой радиусом R с центром в точке F. Таким образом, овал можно считать построенным.

Пусть теперь известны длина и ширина овала, т.е. обе оси симметрии. Проведем две перпендикулярные прямые. Пусть эти прямые пересекаются в точке O. На горизонтальной прямой отложим отрезок AB с центром в точке O, равный длине овала. На вертикальной прямой отложим отрезок CD с центром в точке O, равный ширине овала.

Соединим прямой точки C и B. Из точки O как из центра проведем дугу радиусом OB, соединяющую прямые AB и CD. Точку пересечения с прямой CD назовем точкой E.

Из точки C проведем дугу радиусом CE так, чтобы она пересекала отрезок CB. Точку пересечения обозначим точкой F. Расстояние FB обозначим Z. Из точек F и B как из центров проведем две пересекающие дуги радиусом Z.

Соединяем точки пересечения двух дуг прямой и назовем точки пересечения этой прямой с осями симметрии точками G и H. Отложим точку G* симметрично точке G относительно точки O. И отложим точку H* симметрично точке H относительно точки O.

Соединяем точки H и G*, H* и G*, H* и G прямыми линиями. Обозначим расстояние HC как R, а расстояние GB как R*.

Из точки H как из центра проведем дугу радиусом R, пересекающую прямые HG и HG*. Из точки H* как из центра проведем дугу радиусом R, пересекающую прямые H*G* и H*G. Из точек G и G* как из центров проведем дуги радиусом R*, замыкая получившуюся фигуру. Построение овала закончено.

Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.

Рассмотрим все случаи построения на конкретных примерах.

Построение отрезка, равного данному

Есть отрезок СD. Задача - начертить равнозначный данному отрезок той же величины.

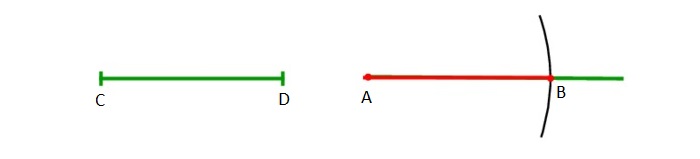
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).

Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.

Отрезок AB будет равнозначен отрезку СD. Задача решена.

Деление отрезка пополам

Имеется отрезок AB.

Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.

Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.

Построение угла, равного данному

Имеется угол ABC.

Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.

Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.

Построение перпендикулярных прямых

Пример 1

Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.

Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Намечаются два отрезка - AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.

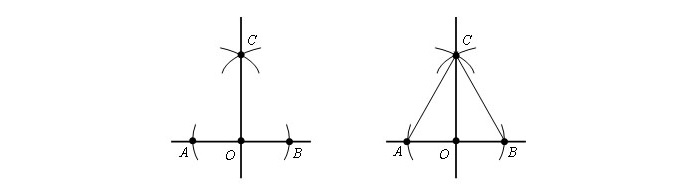
Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O₁ - место их соприкосновения.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО₁ и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO₁A. Из данного вывода следует, что угол OAC = O₁AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).

Исходя из этого, выводим, что угол OCA = O₁CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

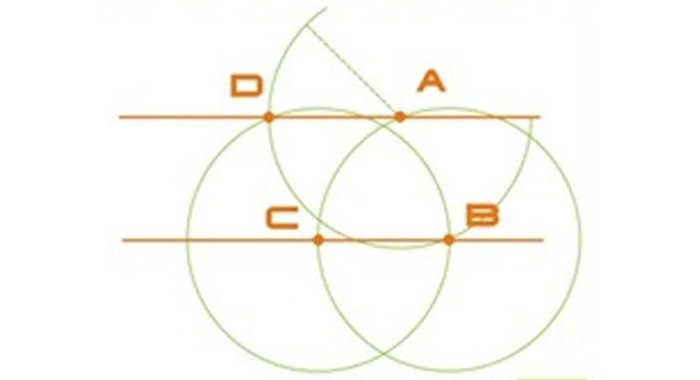
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

Отметить отрезок AB, чья длина будет равняться а.

Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

Построение правильного четырехугольника вписанного в окружность

Вариант 1

Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

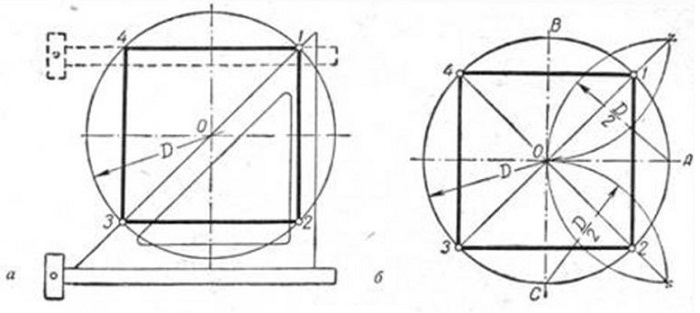
Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

Построение вписанного в окружность правильного пятиугольника

Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.

Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

Построение правильного шестиугольника, вписанного в окружность

Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.

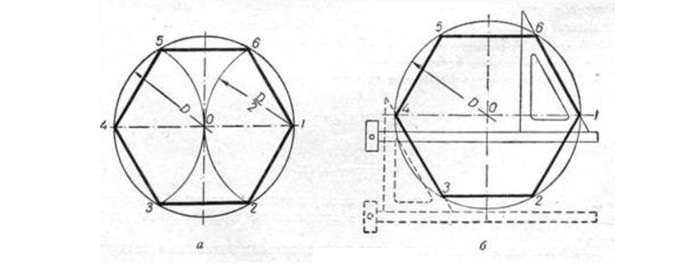
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

Читайте также: