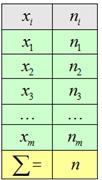Как сделать кривую распределения результатов

Добавил пользователь Валентин П.
Обновлено: 05.10.2024

Цель работы: овладение студентом способами построения эмпирической и теоретической (нормальной) кривой распределения; выработка умения и навыков применения критериев согласия для проверки выдвинутой статистической гипотезы.

Содержание работы: на основе дискретного вариационного ряда, полученного в лабораторной работе № 1, выполнить следующее:

1. Построить эмпирическую (полигон) и теоретическую (нормальную) кривую распределения.
2. Проверить согласованность эмпирического распределения с теоретическим нормальным, применяя три критерия:
- а) критерий Пирсона;
- б) один из критериев: Колмогорова, Романовского, Ястремского;
- в) приближенный критерий.
Методика выполнения работы

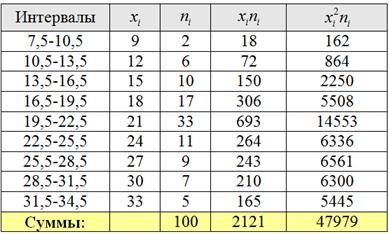
Продолжим вероятностно-статистическую обработку результатов эксперимента, предложенных в лабораторной работе № 1, то есть число рабочих дней без простоя. За основу берем дискретный вариационный ряд в табл.

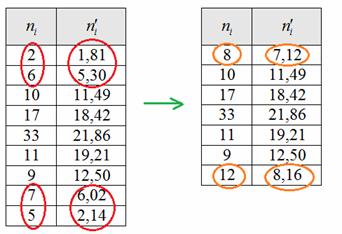
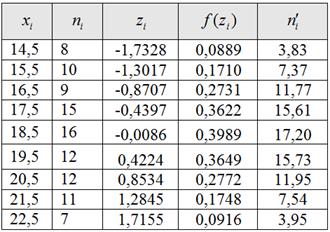
Эмпирическая кривая распределения представляет собой полигон частот (см. лабораторную работу № 1). Для построения теоретической (нормальной) кривой найдем координаты точек , для чего рассчитаем теоретические частоты (табл.).

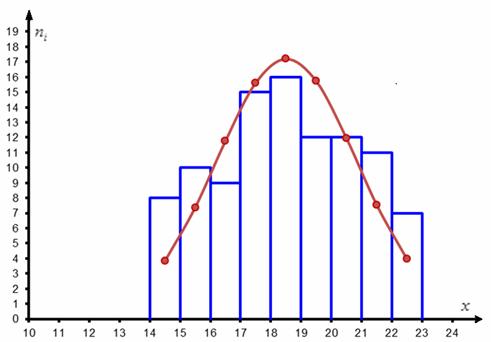
Строим эмпирическую и теоретическую кривые (рис.).

дискретный вариационный статистика выборка

Рис. 1 Эмпирическая и теоретическая кривые

Проверим согласованность эмпирического распределения (число рабочих дней без простоя) с теоретическим нормальным по критерию Пирсона. Вычислим величину по формуле:

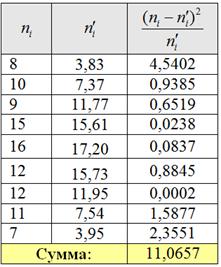
Для нахождения суммы составляем расчетную табл.

Находим число степеней свободы

Выбираем уровень значимости . По таблице критических точек распределения (приложение 5) находим . Так как , то делаем вывод, что данные выборки, характеризующие число рабочих дней без простоя, не подчиняются нормальному закону распределения.

Проведём проверку близости эмпирического распределения к нормальному по критерию Романовского. Вычислим, согласно (32), величину . Так как , , то , т.е. расхождение между эмпирическим и теоретическим распределением несущественно, что позволяет утверждать, что данные выборки, характеризующие число рабочих дней без простоя по критерию Романовского подчиняются нормальному закону распределения. К такому же выводу мы приходим, применяя критерий Колмогорова.

Наконец, проведём проверку близости рассматриваемой выборки к нормальному распределению по приближенному критерию, используя выборочные статистики: асимметрию, эксцесс и их средние квадратические отклонения. В лабораторной работе № 1 были найдены . Средние квадратические отклонения для асимметрии и эксцесса находим по формулам

то делаем вывод, что данные выборки, характеризующие число рабочих дней без простоя, не подчиняются нормальному закону распределения.

Итак, для проверки согласованности эмпирического распределения с теоретическим нормальным мы применили 4 критерия, два из них подтвердили близость выборочной совокупности к нормальному распределению. Однако, учитывая, что критерий Колмогорова является более мощным, чем критерий 2 Пирсона, и подтверждает близость рассматриваемой выборки к нормальному распределению, окончательно заключаем, что за закон распределения признака Х -- число рабочих дней без простоя -- можно принять нормальное распределение.

Итак, после разгрома двух десятков задач ставим вишенку на торт статистических гипотез, а именно разбираем важнейшую гипотезу о виде (законе) распределения и распространённые тематические примеры. Кино тоже будет.

Рассмотрим генеральную совокупность, распределение которой неизвестно. Однако есть основание полагать, что она распределена по некоторому закону (чаще всего, нормально). Это предположение может появиться как до, так и в результате статистического исследования, когда мы извлекли и изучили выборку объёма .

И нам требуется на уровне значимости проверить нулевую гипотезу – о том, что генеральная совокупность распределена по закону против конкурирующей гипотезы о том, что она по нему НЕ распределена.

Как проверить эту гипотезу? Постараюсь объяснить кратко. Как вы знаете, выборочные данные группируются в дискретный или интервальный вариационный ряд с вариантами и соответствующими частотами

Поскольку эти данные взяты из практического опыта, то выборочный вариационный ряд называют эмпирическим рядом, а частоты – эмпирическими частотами.

Далее строятся графики, рассчитываются выборочные характеристики (выборочная средняя , выборочная дисперсия и другие), словом, выполняются все те хорошие дела, которыми мы занимались на протяжении многих уроков.

И возникает вопрос: значимо или незначимо различие между эмпирическими и соответствующими теоретическими частотами?

Для ответа на это вопрос рассматривают различные статистические критерии, которые называют критериями согласия, и наиболее популярный из них разработал Карл Пирсон:

При достаточно большом (объёме выборки) распределение этой случайной величины близкО к распределению хи-квадрат с количеством степеней свободы , где – количество оцениваемых параметров закона .

…всем понятно, почему величина случайная? – по той причине, что в разных выборках мы будем получать разные, заранее непредсказуемые эмпирические частоты.

Далее строится правосторонняя критическая область:

Критическое значение можно отыскать с помощью соответствующей таблицы или Экселя (Пункт 11б).

Наблюдаемое значение критерия рассчитывается по эмпирическим и найденным теоретическим частотам:

Если , то на уровне значимости нет оснований отвергать гипотезу о том, что генеральная совокупность распределена по закону . То есть, различие между эмпирическими и теоретическими частотами незначимо и обусловлено случайными факторами (случайностью самой выборки, способом группировки данных и т.д.)

Если , то нулевую гипотезу отвергаем, иными словами эмпирические и теоретические частоты отличаются значимо, и это различие вряд ли случайно.

Обратите внимание на формулировку, которую я выделил жирным цветом – такая формулировка напоминает нам о том, что принятие статистической гипотезы ещё не означает её истинность, поскольку существует -вероятность того, что мы приняли неправильную гипотезу (совершили ошибку второго рода).

И, наконец, ~~бараны~~ коровы, которые нас уже заждались. Реалистичность фактических данных оставлю на совести автора методички сельскохозяйственной академии:

По результатам выборочного исследования найдено распределение средних удоев молока в фермерском хозяйстве (литров) от одной коровы за день:

На уровне значимости 0,05 проверить гипотезу о том, что генеральная совокупность (средний удой коров всей фермы) распределена нормально. Построить эмпирическую гистограмму и теоретическую кривую.

…если не любите молоко, то пусть это будет чай, сок, пиво или какой-то другой напиток, который вам нравится :) Чтобы было интереснее исследовать эту волшебную ферму.

Решение: на уровне значимости проверим гипотезу о нормальном распределении генеральной совокупности против конкурирующей гипотезы о том, что она так НЕ распределена. Используем критерий согласия Пирсона .

Эмпирические частоты известны из предложенного интервального ряда, и осталось найти теоретические. Для этого нужно вычислить выборочную среднюю и выборочное стандартное отклонение .

Выберем в качестве вариант середины частичных интервалов (длина каждого интервала ) и заполним расчётную таблицу:

Внимание! Если вы не понимаете, как заполнять эту таблицу, или не знаете, как это сделать быстро, то обязательно обратитесь к Примеру 16, там есть все объяснения и видео!

Вычислим выборочную среднюю:
литра

Выборочную дисперсию вычислим по формуле:

И выборочное стандартное отклонение:
литра.
По причине большого объёма выборки его исправлением можно пренебречь.

Теоретические частоты рассчитываются по формуле:
, где – знакомая функция Гаусса, а .

Все вычисления удобно проводить в Экселе и на всякий случай я распишу одну строчку:

– здесь выгодно использоваться встроенную экселевскую функцию =НОРМРАСП(-2,23; 0; 1; 0), первый аргумент которой равен текущему значению . За неимением Экселя и калькулятора пользуйтесь стандартной таблицей, которая есть практически в любой книге по терверу.

И, наконец, теоретическая частота:
, довольно часто её округляют до целого значения, но без округления результат всё же точнее.

Надеюсь, на данный момент уже все умеют протягивать (копировать) формулы по образцу, а если нет, то я всё равно научу :) Решил таки записать отдельный ролик, хотя особой технической новизны тут нет:

Как проверить гипотезу о норм. распределении генеральной совокупности? (Ютуб)

Дальнейшая задача состоит в том, чтобы оценить, насколько ЗНАЧИМО отличаются эмпирические частоты (ступеньки гистограммы) от соответствующих теоретических частот (уровень коричневых точек).

Но перед тем, как сравнивать теоретические и эмпирические частоты, следует объединить интервалы с малыми (меньше пяти) частотами. В данном случае объединяем два первых и два последних интервала, для этого суммируем частоты, обведённые красным цветом, и получаем оранжевые результаты:

Это нужно для того, чтобы сгладить неоправданно большое расхождением между малыми частотами по краям выборки. Действие не обязательное, но крайне желательное, ибо студентов на моей памяти часто заставляли переделывать задание.

Найдём критическое значение критерия согласия Пирсона. Количество степеней свободы определяется по формуле , где – количество интервалов, а – количество оцениваемых параметров рассматриваемого закона распределения.

Так как мы объединяли интервалы, то теперь их не девять, а .
У нормального закона мы оцениваем параметра.

Пояснение: – это оценка неизвестного генерального матоожидания, а – это оценка неизвестного генерального стандартного отклонения, итого два оцениваемых параметра.

Таким образом, и для уровня значимости :

Это значение можно найти по таблице критических значений распределения хи-квадрат или с помощью Калькулятора (Пункт 11б).

При нулевая гипотеза отвергается, а при таких оснований нет:

Вычислим наблюдаемое значение критерия (суть – сумму расхождений между частотами), и для этого удобно заполнить ещё одну расчётную табличку:

На всякий пожарный пример расчёта: .

В нижней строке таблицы у нас получилось готовое значение , поэтому на уровне значимости 0,05 гипотезу о нормальном распределении генеральной совокупности отвергаем.

Иными словами различие между эмпирическими и теоретическими частотами статистически значимо и вряд ли объяснимо случайными факторами. При этом с вероятностью 5% мы совершили ошибку 1-го рода (то есть, ген. совокупность на самом деле распределена нормально, но мы это отвергли).

Ответ: на уровне значимости 0,05 гипотезу о нормальном распределении отвергаем

В чём может быть причина? Ведь по теореме Ляпунова большинство коров не оказывает практически никакого влияния на удой других коров, и поэтому распределение ген. совокупности должно быть близкО к нормальному.

Причины могут быть разными. Например, неоднородный состав совокупности (коровы разной породы), или на ферме есть VIP-хлев, где коровы получают улучшенное питание :) А может быть, некоторые коровы больны и как раз оказывают существенное влияние на остальных, в связи с чем нарушается условие теоремы Ляпунова.

Интересно отметить, что при уменьшении уровня значимости до 0,01 критическое значение , и гипотеза о нормальном распределении уже принимается. Однако не нужно забывать, что здесь выросла -вероятность того, что мы приняли неправильную гипотезу. С оценкой этой вероятности можно ознакомиться в специализированной литературе по статистике.

И, конечно, в случае сомнений имеет смысл увеличить объём выборки, чтобы провести повторное исследование.

На основании исследования выборки выдвинуть гипотезу о законе распределения генеральной совокупности

То есть, здесь не говорится о том, что предполагаемый закон нормальный (или какой-то другой) – этот вопрос вам предлагается проанализировать самостоятельно.

Каким образом это можно сделать?

Во-первых, гипотезу можно выдвинуть априорно, даже не исследуя выборку, и зависеть она будет от содержания задачи. Так, для коров используем упомянутую выше теорему Ляпунова: если каждый объект совокупности оказывает несущественное влияние на всю совокупность, то её распределение близкО к нормальному. Если речь идёт о погрешностях округления, то распределены они обычно равномерно. Если распадаются радиоактивные изотопы, то, скорее всего, по экспоненциальному закону. И так далее.

Построенная гистограмма по форме напоминает колоколообразный график плотности нормального распределения, и это является веской причиной предположить, что генеральная совокупность распределена нормально. Да, здесь есть слишком высокий средний столбик, но, возможно, это просто случайность выборки.

Если столбики примерно одинаковы по высоте, то предполагаем, что генеральная совокупность распределена равномерно. Для показательного распределения тоже будет своя, характерная гистограмма.

В случае дискретных распределений тоже никаких проблем – строим полигон и смотрим, на что он похож.

Следующие признаки аналитические, приведу их для нормального распределения:

1) У нормального распределения математическое ожидание совпадает с модой и медианой. В нашем случае соответствующие выборочные показатели весьма близкИ друг к другу (матожидание оценивается выборочной средней):

Желающие могут рассчитать моду и медиану самостоятельно. Впрочем, желающими часто становятся поневоле, поскольку задача, которую мы рассматриваем, нередко идёт в комплексе со всеми этими заданиями.

– и в него действительно попадают все коровы!

3) Коэффициенты асимметрии и эксцесса нормального распределения равны нулю. В нашем случае эти характеристики не сказать что сильно, но довольно близкИ к нулю:

На практике в исследование желательно включить все пункты за исключением, возможно, третьего (т.к. асимметрию и эксцесс рассчитывают далеко не всегда).

Следует отметить, что перечисленные выше предпосылки ещё не означают, что соответствующая гипотеза будет принята, в чём мы недавно убедились. А если гипотеза и окажется принятой, то это всё равно на 100% не гарантирует нормальность генеральной совокупности (так как существует -вероятность совершить ошибку 2-го рода – принять неверную гипотезу).

Если вы не прорешали предыдущие пункты, то настоятельно рекомендую это сделать, ну или просто взять готовые числа из образца:

6) По найденным характеристикам сделать вывод о законе эмпирического ряда распределения.

7) Построить нормальную кривую по опытным данным на графике гистограммы.

8) Произвести оценку степени близости теоретического распределения эмпирическому ряду с помощью критерия согласия Пирсона на уровне значимости 0,05.

Как видите, Пункт 6 как раз на обоснование предполагаемого закона распределения. Краткое решение в конце этого урока.

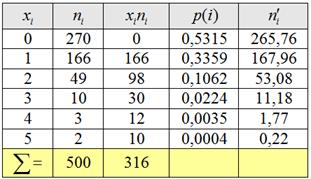
В результате проверки 500 контейнеров со стеклянными изделиями установлено, что число повреждённых изделий имеет следующее эмпирическое распределение:

( – количество повреждённых изделий в контейнере, – количество контейнеров)

С помощью критерия согласия Пирсона на уровне значимости 0,05 проверить гипотезу о том, что случайная величина – число повреждённых изделий распределена по закону Пуассона.

…здесь тоже представьте изделия по своему интересу :)

Все числа уже забиты в макет, придерживайтесь следующего алгоритма:

2) Находим значения для . Вычисления можно проводить на обычном калькуляторе, но удобнее использовать экселевскую функцию =ПУАССОН, Калькулятор (Пункт 7) в помощь.

3) Находим теоретические частоты

5) Рассчитываем наблюдаемое значение критерия и делаем вывод.

Примерный образец чистового оформления задачи в конце урока.

Помимо разобранных примеров, в задачнике В. Е. Гмурмана можно найти аналогичные задачи для биномиального, равномерного и показательного распределения, но лично в моей практике они почти не встречались.

Ну а этот урок и тема подошли к концу, и я надеюсь, вам было хорошо. Но математическая статистика ни в коем случае не закончилась! – есть ещё порох, есть зажигательные разделы, о которых нужно непременно рассказать.

Желаю успехов и до скорых встреч!

Решения и ответы:

Пример 20. Решение (продолжение):

6) Проанализируем полученные результаты:

Форма гистограммы похожа на нормальную кривую.

Выборочная средняя, мода и медиана достаточно близкИ друг другу:

Построим интервал :

– в данный интервал попали все выборочные значения.

Асимметрия практически равна нулю , однако, эксцесс отличается значительно .

Перечисленные признаки позволяют предположить, что генеральная совокупность распределена нормально.

7) Найдём теоретические частоты:
, где , ,
в данной задаче :

Построим эмпирическую гистограмму и теоретическую кривую:

8) Проверим гипотезу о том, что генеральная совокупность распределена нормально. Используем критерий согласия Пирсона. Для уровня значимости и количества степеней свободы по соответствующей таблице находим критическое значение:

При выдвинутую гипотезу отвергаем, а при нет оснований отвергать гипотезу.

Вычислим наблюдаемое значение критерия . Заполним расчётную таблицу:

В результате: , поэтому на уровне значимости 0,05 нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности.

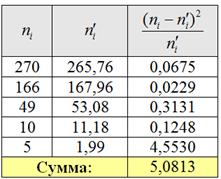
Пример 54. Решение: проверим гипотезу о том, что генеральная совокупность распределена по закону Пуассона. Используем критерий согласия Пирсона. Вычислим произведения , выборочную среднюю и теоретические частоты по формуле , где .
Вычисления сведём в таблицу:

Объединяем две последние варианты ввиду их малых частот и находим критическое значение для уровня значимости и количества степеней свободы :

Вычислим наблюдаемое значение критерия :

Таким образом, , поэтому на уровне значимости нет оснований отвергать гипотезу о том, что генеральная совокупность распределена по закону Пуассона.

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Этот метод оценки точности применяется в условиях производства большого количества деталей. Для его применения необходимо произвести выборку деталей из производимых на исследуемой операции. По результатам измерения деталей выборки строится опытная кривая распределения, к которой по критерию согласия подбирается теоретический закон распределения. Для построения опытной кривой распределения по оси абсцисс откладывают измеряемую величину, например, диаметр детали, через определенные интервалы, а по оси ординат их количество, попадающее в эти интервалы, или частости. Частость — это отношение числа деталей, попавших в данный интервал размеров, к общему числу деталей выборки. Соединяя точки пересечения, получают ломаную кривую, которая называется опытной кривой распределения, или полигоном распределения деталей по размерам (рис. 6.1).

Рис. 6.1. Опытная кривая, или полигон распределения размеров

Определяют числовые характеристики опытного закона распределения:

статистическое среднее

Согласно закону больших чисел при неограниченном увеличении числа наблюдений п х приближается к математическому ожиданию случайной величины. Статистическое среднее х позволяет судить о центре группирования изучаемой статистической совокупности;

статистическую дисперсию

статистическое среднее квадратическое отклонение

Распределение размеров деталей на операциях механической обработки в большинстве случаев подчиняется закону нормального распределения случайных величин. Это позволяет использовать указанный закон для анализа точности рассматриваемой операции. Основная цель анализа точности обработки в партии деталей — определение вероятного количества бракованных и годных деталей на исследуемой операции.

Для нормального закона распределения плотность вероятности или дифференциальная функция распределения имеет вид

где х — переменная случайная величина;

т_х — математическое ожидание (центр группирования) величины jc;

о_х — стандартное среднее квадратическое отклонение случайной величины х.

Дифференциальная функция нормального распределения графически выражается в виде симметричной кривой — кривой Гаусса (рис. 6.2).

Рис. 6.2. Дифференциальная функция нормального распределения

Функция нормального распределения (интегральный закон) имеет

Величина F(x) определяет вероятность попадания случайной величины в интервал (хь *2).

Для облегчения вычислений формулу интегрального закона нормального распределения с помощью нормирующего множителя и, учитывая, что можно привести к виду

Интеграл называют нормированной функцией

Лапласа и его значения для различных t приводят в таблицах значений функции Лапласа. При использовании этих таблиц решение задачи по определению вероятности того, что случайная величина х находится в пределах (хь хг), сводится к нахождению разности между двумя значениями функции Лапласа

При использовании формулы следует иметь в виду тождество Ф(/) =

Для практических применений зона рассеяния случайной величины х, подчиняющейся закону нормального распределения, ограничивается пределами ±3а* и составляет 6а*. При этом t = — 3 и ti = 3.

Правило трех о: площадь, лежащая за пределами трехсигмового интервала, равна q = 1 — 0,9973 = 0,0027.

Параметры нормального закона распределения т_х и а* определяют по методу максимального правдоподобия, m_x=x;D = S 2 ; о_х — S.

Метод кривых распределения позволяет определить:
- 1) точность процесса по количеству единиц допуска;
- 2) величину поднастройки станка Н = т_х -х;
- 3) процент исправимого брака;
- 4) процент неисправимого брака;
- 5) _ увеличение годных деталей (уменьшение брака) при совмещении Хс т_х.
Недостатком метода является то, что он обращен в прошлое, когда детали уже изготовлены и ничего для проверяемых изделий предпринять нельзя. Он не позволяет распознать каждую из действующих причин возникновения погрешностей. Метод громоздок в расчетах.

К преимуществам метода следует отнести то, что он интегрально и точно дает представление о точности и качестве изделий.

Каждый исследователь знает: для того, чтобы его работа приобрела статус научной, от него требуется качественная и количественная обработка результатов с применением математических методов. С их помощью вы получите ряд цифр и статистически значимых гипотез. Если кроме этого вы хотите наглядно представить полученные вами данные, обратите внимание на то, как строить графики распределения признака.
- Как построить график распределения
- Как построить кумуляту
- Как построить нормальное распределение
Распределение признака указывает, какое значение встречается чаще всего. Поэтому задача сравнения по распределению в уровне признака состоит в том, чтобы сопоставить классы (полученные данные) испытуемых по их частоте.

Выделяют два типа задач:
- выявление различий между двумя эмпирическими распределениями;
- выявление различий между эмпирическим и теоретическим распределениями.В первом случае мы будем сравнивать ответы или данные двух выборок, полученных в ходе собственного исследования. Например, успеваемость по результатам летней сессии студентов биологов и физиков. Во втором случае мы сопоставляем полученные опытным путем результаты с уже имеющимися нормами в литературных источниках. Например, можно посмотреть, будут ли проявляться различия по анатомо-физиологическим параметрам между современными подростками и составленными несколько десятилетий назад по их ровесникам нормами.

График распределения признака строится с помощью оси Х, на которой в ранжированном порядке отмечаются полученные значения, и оси Y, которая показывает частоту встречаемости этих значений. Сам же график будет представлять собой кривую распределения. Его необходимо будет проверить на нормальность распределения.

Распределение признака считается нормальным, если А=Е=0, где А – это асимметрия распределения, а Е – эксцесс.

Для составления графика распределения признака и его проверки на нормальность мы можем применить метод Н.А. Плохинского. Он состоит из трех этапов:- Вычисляем А асимметрию (А=(∑〖(xi-〖xср.)〗^3〗)/〖nS^3) и Е эксцесс (Е=(∑〖(xi-〖xср.)^4-3)/〖nS〗^4), где Хi – каждое конкретное значение признака, Хср. – среднее значение признака, n – объем выборки, S - стандартное отклонение.- Рассчитываем ошибки репрезентативности, то есть отклонения выборки от генеральной совокупности ((Ma=√(6/n)), (Me = 2√(6/n)).- Если одновременно выполняется неравенство (|A|)/Ma

Читайте также: