Как сделать каноническое уравнение эллипса

Добавил пользователь Валентин П.
Обновлено: 05.10.2024

Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
\frac>>+\frac>>=1\label
$$
при условии $a \geq b > 0$.

Из уравнения \eqref следует, что для всех точек эллипса $|x| \leq a$ и $|y| \leq b$. Значит, эллипс лежит в прямоугольнике со сторонами $2a$ и $2b$.

Точки пересечения эллипса с осями канонической системы координат, имеющие координаты $(a, 0)$, $(-a, 0)$, $(0, b)$ и $(0, -b)$, называются вершинами эллипса. Числа $a$ и $b$ называются соответственно большой и малой полуосями эллипса.

В каноническое уравнение входят только квадраты координат. Поэтому, если координаты $(x, y)$ какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты $(-x, y)$, $(x, -y)$ и $(-x, -y)$ точек $M_$, $M_$ и $M_$ (рис. 8.1). Следовательно, справедливо следующее утверждение.

Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.

Внешний вид эллипса проще всего описать сравнением с окружностью радиуса $a$ с центром в центре эллипса: $x^+y^=a^$. При каждом $x$ таком, что $|x| Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении \(b/a$.

Фокусы, эксценриситет и директрисы эллипса.

У эллипса есть две замечательные точки, которые называются его фокусами.

Фокусами называются точки $F_$ и $F_$ с координатами $(c, 0)$ и $(-c, 0)$ в канонической системе координат (рис. 8.3).

Рис. 8.3. Фокусы эллипса.

Для окружности $c=0$, и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.

Отметим, что \(\varepsilon Утверждение 2.

Расстояние от произвольной точки $M(x, y)$, лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы $x$:
$$
r_=|F_M|=a-\varepsilon x,\ r_=|F_M|=a+\varepsilon x.\label
$$

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса $2a$.

Необходимость. Если мы сложим равенства \eqref почленно, то увидим, что
$$
r_+r_=2a.\label
$$
Достаточность. Пусть для точки $M(x, y)$ выполнено условие \eqref, то есть
$$
\sqrt<(x-c)^+y^>=2a-\sqrt<(x+c)^+y^>.\nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^=a\sqrt<(x+c)^+y^>.\label
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение \eqref. Мы придем к $b^x^+a^y^=a^b^$, равносильному уравнению эллипса \eqref.

Рис. 8.4. Фокусы и директрисы эллипса.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса $\varepsilon$.

Уравнение касательной к эллипсу.

Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть $M_(x_, y_)$ — точка на эллипсе и $y_ \neq 0$. Через $M_$ проходит график некоторой функции $y=f(x)$, который целиком лежит на эллипсе. (Для $y_ > 0$ это график $f_(x)=b\sqrt/a^>$, для \(y_ Утверждение 5.

Касательная к эллипсу в точке $M_(x_, y_)$ есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.

Определение. Эллипс - это замкнутая плоская кривая, которая имеет уравнение x²/a²+y²/b²=1. Это каноническое уравнение эллипса, в нем координатные оси совпадают с осями эллипса.

Он имеет два фокуса. Это такие точки, сумма расстояний от которых до любой P(x,y) есть постоянная величина. Эллипс также можно описать как пересечение плоскости и кругового цилиндра.

Эллипс

Элементы:

F₁ , F₂ – фокусы . F₁ = ( c ; 0); F ₂ (- c ; 0)
A₁ A₂ - большая ось;
B₁ B₂ - малая ось;
О - центр эллипса (пересечения малой и большой осей);
A₁, A₂, B₁, B₂ - вершины эллипса;
Диаметр эллипса - отрезок, соединяющий две точки эллипса и проходящий через O;
с – фокусное расстояние, половина расстояния между F₁ и F₂;
a – большая полуось эллипса;
b – малая полуось;
r₁ и r₂ - фокальные радиусы эллипса;
если a > b, то уравнения директрис эллипса x=-a/e, x=a/e;
если a 2 /a - отрезок, который соединяет фокус фигуры и точку на кривой, перпендикулярен ее большей оси.

Теорема. Фокусное расстояние c и полуоси эллипса связаны соотношением:

Доказательство: В случае, если М лежит на пересечении кривой с вертикальной осью, r₁ + r₂ = 2*(по теореме Пифагора). В случае, если М - пересечение его с горизонтальной осью, r₁ + r₂ = а – c + а + c. Т.к. по определению сумма r₁ + r ₂ – постоянна, то , приравнивая, получаем:

Основные свойства эллипсa

Угол между касательной к эллипсу и фокальным радиусом r₁ равен углу между касательной и радиусом r₂. Лучи, выпущенные из одного фокуса, после отражения соберутся во втором фокусе.
Уравнение касательной к эллипсу в М с координатами (x_M, y_M): .
Если две параллельные прямые пересекают эллипс, то отрезок соединяющий середины отрезков образовавшихся при пересечении прямых и эллипса, всегда будет проходить через (.) O эллипсa. (Это свойство дает возможность находить центр эллипса.)
При равенстве полуосей эллипс превращается в окружность.
Эллипс это коническое сечение. Он может быть получен как пересечение плоскости с конусом.

Уравнение

Каноническое уравнение в декартовой системе координат, центр в начале координат, большая ось на оси абсцисс: . Эллипс - кривая второго порядка. Координаты x и y входят только в четных степенях, поэтому эллипс симметричен относительно осей координат. Оси координат пересекают эллипс в A₁(-a,0), A₂(a,0), B₁(0,-b), B₂(0,b). Эллипс лежит в прямоугольнике 2a и 2b.
Центр смещен в ( x_o, y_o):
Параметрическое: , где 0 ≤ α ≤ 2 π.
В полярной системе координат: , где полюс полярной системы координат левый фокус F₁, полярная ось луч F₁ , F₂, p = b²/a фокальный параметр.

Радиус круга вписанного в эллипс

Круг, вписанный в эллипс касается только двух вершин эллипсa B₁ и B₂. Соответственно, радиус вписанного круга будет равен длине малой полуоси эллипсa r = b.

Радиус круга описанного вокруг эллипсa

Круг, описанный вокруг эллипсa касается только двух вершин эллипсa A₁ и A₂. Соответственно, радиус описанного круга R будет равен длине большой полуоси эллипсa R = a.

Как построить эллипс

П е р в ы й с п о с о б.

Сумма расстояний от любой точки эллипсa до его фокусов величина постоянная равная 2а.

Иголки втыкаем в фокусы F₁ , F₂.
К иголкам привязываем нитку длинной 2а.
Нитку оттягиваем карандашом и чертим.

В т о р о й с п о с о б.

Проводим две концентрические окружности радиуса a и b.
Через центр О проводим произвольный луч ON.
Через точки K и M, в которых луч ON пересекает окружности, проводим прямые соответственно параллельные осям Ox и Oy.
Точка их пересечения L - точка искомого эллипса.
Меняя направление луча ON, получим новые точки эллипсa.

Эксцентриситет эллипса

Определение. Форма эллипса определяется характеристикой, которая равна отношению е = с/a называется эксцентриситетом, характеризует вытянутость фигуры. Чем эксцентриситет ближе к нулю, тем линия больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.

Пример 2. Дана кривая 9x 2 + 25y 2 = 225. Найти: 1) показать, что это эллипс, найти его полуоси 2) эксцентриситет 3) директрисы.

Разделим обе стороны на 225

сократим, получим каноническое уравнение эллипса

Следовательно, 1) полуоси a = 5, b = 3, 2) F₁(-c, 0), F₂(c, 0) с определим из равенства b 2 = a 2 - c 2 , c 2 = a 2 - b 2 = 25 - 9 = 16, c = 4, поэтому левый фокус F₁(-4, 0), правый F₂(4, 0).

4) уравнение директрис x = ±a/e =±5*5/4=±25/4.

Пример 3. Эксцентриситет e = 1/3, центр его совпадает с началом координат, F₁ (-2;0). Вычислить расстояние от точки M₁ с абсциссой, равной 2, до директрисы, односторонней с данным фокусом.

Т.к. F₁ (-2;0), то с = 2. Зная с и e = 1/3, определим а. e = c/a, а = c/е = 2*3=6. Уравнение директрисы x = -а/e = -6*3 = -18. Точка M₁ имеет координату х = 2. Следовательно, d = |-18|+2=20.

Пример 4. Определить точки эллипса x 2 /100+y 2 /36 =1, расстояние от которых до F₂ равно 14. Найти директрисы.

a = 10, b = 6, c 2 = а 2 - b 2 = 100 -36 = 64 = 8 2 . Найдем эксцентриситет е = c/а = 8/10 = 4/5. Используем формулу для r₂ = а - еx, 14 = 10 - 4/5*x, отсюда х = -5. Подставим в исходное координату х и найдем у = ±√27 = ±3√3. Условиям задачи удовлетворяют точки (-5; 3√3) и (-5; -3√3).
Уравнения директрис x = ±a/e = ±10/4/5 = ±25/2 = ±12,5.

Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.

Эллипс – фокусное расстояние, уравнение, свойства и эксцентриситет фигуры обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру

Что такое эллипс и фокусное расстояние

Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .

Обозначим фокусы эллипса и . Допустим, что расстояние = – фокусное расстояние.

– половина расстояния между фокусами;

Фокусное расстояние и полуоси связаны соотношением:

Если точка находится на пересечении эллипса с вертикальной осью, (теорема Пифагора). Если же точка находится на пересечении его с горизонтальной осью, . Так как по определению сумма – постоянная величина, то приравнивая получается:

Уравнение эллипса

Уравнение элиппса бывает двух видов:

Каноническое уравнение эллипса.
Параметрическое уравнение эллипса.

Сначала рассмотрим каноническое уравнение эллипса:

Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:

Если центр эллипсa смещен в точку с координатами тогда уравнение:

Чтобы получить каноническое уравнение эллипса, разместим и на оси симметричной к началу координат. Тогда у фокусов будут такие координаты и (см. рис. 2).

Пусть – произвольная точка эллипса. Обозначим через и – расстояние от точки к фокусам. Согласно с определением эллипса:

Подставим в (1) , и освободимся от иррациональности, подняв обе части к квадрату, получим:

(подносим к квадрату обе части): ,

Обозначим: , получаем каноническое уравнение эллипса:

Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из у нас получается . Так как , тогда , и поэтому .

Для построения эллипса обратим внимание, что если точка принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки тоже удовлетворяют это уравнение: из

Точки – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.

Из уравнения (2) находим , для первой четверти .

Если , тогда . Если же , тогда . Точки и , а также симметричные с ними , – вершины эллипса, точка – центр эллипса, = большая ось, – малая ось эллипса.

Если первой четверти, тогда из получается, что при возрастании от к значение падает от к . (рис. 3)

Параметрическое уравнение выглядит так:

Основные свойства эллипса

Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.

1. Угол между касательной к эллипсу и фокальным радиусом равен углу между касательной и фокальным радиусом .

2. Уравнение касательной к эллипсу в точке с координатами :

3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).

4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.

5. Если вписать эллипс с фокусами и у треугольника , тогда выполняется соотношение:

Эксцентриситет эллипса

Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается

Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда – получается круг. Если же , тогда – эллипс превращается в отрезок. В некоторых случаях . Для фокальных радиусов приведём без доказательства такие формулы:

Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и , тогда вычислим – полуфокусное расстояние.

Строим фокусы и на расстоянии один от другого Концы не растянутой нити длиной закрепляем в точках и . Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.

Примеры решения задач

Задача

Задан эллипс уравнением и точки . Необходимо:

убедиться, что точки и лежат на эллипсе;
найти полуоси эллипса и координаты его фокусов;
найти расстояние от точки к фокусам;
убедиться, что сумма этих расстояний равна длине большой оси;
найти эксентриситет эллипса.

Решение

1. Подставим координаты точки в левую часть уравнения эллипса:

– точка лежит на эллипсе. Аналогично для :

точка лежит на эллипсе.

2. С канонического и данного уравнения эллипса выходит: Из равенства получается:

– полуфокусное расстояние. Координаты фокусов и .

3. Найдём фокальные радиусы точки :

4. Найдём сумму , что отвечает определению эллипса.

5. Эксцентриситет находится по формуле .

Задача

Найти оси, вершины и фокусы эллипса

Решение

Сведём обычное уравнение к каноническому:

, . Вершины эллипса в точках , , , . Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае больше, чем , то эллипс, который вытянут вдоль оси , находим полуфокусное расстояние .

Фокусы в точках и . (см. рис. 3)

Найти оси, вершины и фокусы эллипса или . Построить эллипс.

Сравнивая последнее уравнение с уравнением (2), у нас получается:

, . Откуда находим оси эллипса: , и координаты вершин: , , , . Дальше из формулы:

. Значит, фокусами эллипса есть точки: и . Для построения эллипса отложим на осях и вершины соответственно соединим их плавной линией, (см. задачу 1).

Замечание! Если в каноническом уравнении большей полуосью будет , тогда фокусы эллипса будут расположены на оси и тогда .

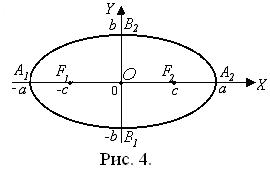
Термины и обозначения основных элементов эллипса (рис. 4):

O – центр эллипса;

с – фокусное расстояние;

F₁(–c; 0), F₂(c; 0) – фокусы эллипса;

|А₁А₂| = 2a– длина большой оси;

а– большая полуось эллипса;

|B₁B₂| = 2b – длина малой оси;

b– малая полуось эллипса.

Для эллипса справедливо: c 2 = a 2 – b 2 .

Число называется эксцентриситетом эллипса .

Если a 2 = b 2 – a 2 .

Если a = b, то уравнение эллипса становится уравнением окружности:

x 2 + y 2 = R 2 ,

В этом случае фокусы эллипса совпадают с центром окружности, фокусное расстояние с = 0, эксцентриситет окружности .

Каноническое уравнение гиперболы:

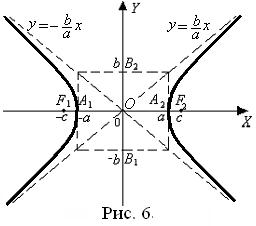
Термины и обозначения основных элементов гиперболы (рис. 6):

O – центр гиперболы;

с – фокусное расстояние;

F₁(–c; 0), F₂(c; 0) – фокусы гиперболы;

|А₁А₂| = 2a– длина вещественной оси;

а– вещественная полуось гиперболы;

|B₁B₂| = 2b – длина мнимой оси;

b– мнимая полуось гиперболы.

Уравнения асимптот гиперболы:

Для гиперболы справедливо: с 2 = a 2 + b 2 .

Число называется эксцентриситетом гиперболы .

Канонические уравнения параболы.

Существуют 4 вида канонических уравнений параболы:

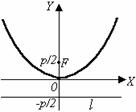	х 2 = 2ру. (16) Фокус F(0; ), уравнение директрисы: у = – .
Рис. 7.
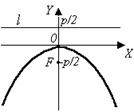	х 2 = –2ру.(17) Фокус F(0; – ), уравнение директрисы: у = .
Рис. 8.
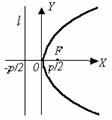	у 2 = 2рх. (18) Фокус F( ; 0), уравнение директрисы: х = – .
Рис. 9.
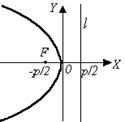	у 2 =–2рх . (19) Фокус F(– ; 0), уравнение директрисы: х = .
Рис. 10.

Термины и обозначения основных элементов параболы: O – вершина параболы, F – фокус параболы, p – параметр параболы (расстояние от фокуса F до директрисы l).

Для приведения уравнения кривой со смещенным центром к каноническому виду может быть использован параллельный перенос системы координат ХОY в точку O₁(α; β). При параллельном переносе координаты любой точки М (х; у) в новой системе координат X₁O₁Y₁ будут (х₁; у₁), где

Читайте также: