Как сделать из обычного уравнения каноническое

Обновлено: 04.07.2024

Уравнение второго порядка вида a 1 ₁x 2 + 2a 1 ₂xy + a 2 ₂y 2 + 2a 0 ₁x + 2a 0 ₂y + a 0 ₀ = 0 определяет на плоскости кривую.
Канонический вид кривой второго порядка: λ₁x 2 + λ₂y 2 , причем:
а) если λ₁>0; λ₂>0 – эллипс, в частности, при λ₁=λ₂ это окружность;
б) если λ₁>0, λ₂ 0) имеем гиперболу;
в) если λ₁=0 либо λ₂=0, то кривая является параболой.

Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.

Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.

Алгоритм перехода кривой второго порядка к каноническому виду

Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0

Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 - 4x) = 2(y+3/2) 2
-(x 2 - 4x + 4) = (y+3/2) 2
-(x - 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x - 2) 2 = 0

Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0

Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1

Теперь о совпадениях: пространственную прямую точно так же обозначают строчными латинскими буквами , как вариант, с подстрочными индексами: . Либо двумя точками, принадлежащими данной прямой: .

И точно так же – её можно задать несколькими способами. Начнём с канонов, точки и направляющего вектора:

Если известна некоторая точка пространства , принадлежащая прямой, и направляющий вектор данной прямой, то канонические уравнения этой прямой выражаются формулами:

Приведённая запись предполагает, что координаты направляющего вектора не равны нулю. Что делать, если одна или две координаты нулевые, мы рассмотрим чуть позже.

Задача 143

Составить канонические уравнения прямой по точке и направляющему вектору

Решение: по соответствующим формулам:

Ответ:

Что следует отметить в этом очень простом примере? Во-первых, полученные уравнения НЕ НАДО сокращать на единицу:

Сократить, точнее, можно, но это режет глаз и создаёт неудобства в ходе решения задач.

А во-вторых, проверка, которая очень легко (и быстро!) выполняется устно:

Далее подставляем координаты точки в найденные уравнения:

– получены верные равенства, значит, координаты точки удовлетворяют нашим уравнениям, и сама точка действительно принадлежит данной прямой.

Проверим, удовлетворяет ли точка уравнениям :
– получены верные равенства, значит, точка действительно принадлежит данной прямой.

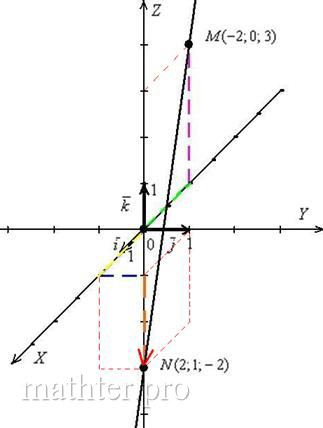
Выполним чертёж в прямоугольной системе координат:

Заодно вспомним, как правильно откладывать точки в пространстве. Строим точку :

– от начала координат в отрицательном направлении оси откладываем отрезок первой координаты (зелёный пунктир);

– в соответствие с третьей координатой отмеряем три единицы вверх (фиолетовый пунктир). Строим точку :

Сама прямая проходит над осью и, если меня не подводит глазомер, над осью . Не подводит, убедился аналитически. Если бы прямая проходила ЗА осью , то следовало бы стереть частичку линии сверху и снизу точки скрещивания.

У прямой бесконечно много направляющих векторов, например:
(красная стрелка). Получился в точности исходный вектор , но это чистая случайность (такую уж я выбрал точку ). Любой коллинеарный вектор, например, тоже будет направляющим вектором данной прямой (вспоминаем, как их получить)

Разберёмся с частными случаями, когда одна или две координаты направляющего вектора нулевые. Попутно продолжим тренировать пространственное воображение. Изобразите в тетради декартову систему координат . Напоминаю удобный масштаб: 2 клетки = 1 ед. – по осям и диагональ одной клетки = 1 ед. – по оси .

Теперь я буду рассказывать о прямых, а вы их мысленно представляйте! Рассмотрим все шесть случаев:

1) Для точки и направляющего вектора канонические уравнения прямой распадаются на три отдельных уравнения:

Что это за прямая?

Задача 144

Составить уравнения прямой по точке и вектору .

Решение и ответ в одну строчку:

2) Канонические уравнения прямой, проходящей через точку параллельно вектору , выражаются формулами .

Такие прямые будут параллельны координатной оси , в частности, уравнения ( любое) задают координатную саму ось ординат.

3) Канонические уравнения прямой, проходящей через точку параллельно вектору , выражаются формулами . Данные прямые параллельны координатной оси , а уравнения ( любое) задают саму ось аппликат.

Обкатываем вторую тройку:

4) Для точки и направляющего вектора канонические уравнения прямой распадаются на пропорцию и уравнение плоскости .

Задача 145

Составить уравнения прямой по точке и вектору .

Решение и ответ в одну строчку:

Аналогично – читаем, вдумываемся и представляем:

5) Прямая, заданная точкой и направляющим вектором , параллельна координатной плоскости , и её канонические уравнения выражаются формулами: . В частности, уравнения определяют прямую, лежащую в плоскости .

6) Прямая, заданная точкой и направляющим вектором , параллельна координ атной плоскости , и её канонические уравнения выражаются формулами: . В частности, уравнения определяют прямую, лежащую в плоскости .

Настала пора закусить – составляем уравнения и вникаем в их смысл:

Задача 146

Записать канонические уравнения прямой, если известна точка и направляющий вектор данной прямой:

Существует несколько различных типов уравнений, описывающих кривую первого порядка, называемую прямой. Каждый из них оптимален для какой-то своей цели. Давайте познакомимся с ними поближе.

Каноническое уравнение прямой в пространстве

Канонический вид уравнения прямой в пространстве выглядит как следующее равенство:

где буквы $(x_0, y_0, z_0)$ используются для обозначения координат любой точки, возлежащей на данной прямой, а $(α, β, γ)$ — координаты направляющего эту прямую вектора, как несложно догадаться, они не могут быть нулевыми.

Не во всех случаях удобно и практично пользоваться каноническим уравнением, поэтому частенько возникает надобность использовать какое-то другое, например, можно прибегнуть к параметрическому.

Для каких прямых не представляется возможным или нельзя написать каноническое уравнение?

Глядя на это уравнение, видно, что его возможно использовать только в том случае, если координаты направляющих векторов исследуемых прямых не равны нулю, для таких прямых стоит воспользоваться параметрическими уравнениями.

Параметрический вид уравнений прямой в пространстве такой:

$\begin x = x_1 + α \cdot λ \\ y = y_1 + β \cdot λ \\ z = z_1 + γ \cdot λ \\ \end$,

где $x_1, y_1, z_1$ — координаты некоторой точки, находящейся на описываемой прямой, $α, β, γ$ — координаты параллельного или лежащего на данной прямой вектора, $λ$ — произвольное число-коэффициент, иногда для его обозначения используют слово “параметр”.

Параметрическое уравнение как раз удобно применять если одна из координат направляющего вектора равна нулю.

Чтобы произвести переход от параметрического вида уравнения к каноническому виду уравнения прямой в пространстве, осуществите вывод канонического уравнения прямой из параметрического.

Готовые работы на аналогичную тему

Для этого следует в к каждом уравнении перенести $λ$ в левую часть, а затем приравнять уравнения. Никакой магии, а только самая что ни на есть пресловутая арифметика:

Уравнение прямой, образуемой пересечением двух плоскостей

Рисунок 1. Связь канонического и общего уравнения прямой

Для того чтобы составить каноническое уравнение прямой в пространстве, заданной пересечением плоскостей, необходимо познакомиться поближе с 2 исследуемыми плоскостями.

Любую плоскость, находящуюся в пространстве, можно описать с помощью равенства:

$Ax + By + Cz + D = 0$,

где $A, B, C$ и $D$ - постоянные, причём $A, B, C$ не могут быть одновременно все нулевыми.

Соответственно, не нужно быть гением, чтобы понять, что если две плоскости пересечены между собой, то на их общей части будет возлежать некая прямая. Чтобы её найти, нужно получить общее решение следующей системы уравнений:

$\begin A_1x + B_1y + C_1z + D_1 = 0 \\ A_2x + B_2y + C_2z + D_2 = 0 \\ \end$

С помощью же частного решения этой системы уравнений можно узнать, принадлежит ли какая-либо точка трёхмерной системы координат описанным уравнениями плоскостям и, конечно же, нашей прямой. Для этого нужно просто подставить её икс, игрек и зет в систему.

Приведённая система уравнений является своеобразной “формулой”, служащей для нахождения общего уравнения прямой в пространстве.

Иногда в каких-либо практических задачах требуется получить из уравнения прямой в пространстве в общем виде параметрические или канонические уравнения, тогда в первую очередь вам стоит узнать координаты её направляющего вектора и какую-либо точку, находящуюся на изучаемой прямой.

Ну что ж, давайте решать нашу задачу. На первом этапе вычислим $x, y, z$ для направляющего вектора.

Найдём нормальные вектора для плоскостей. Если кто забыл, нормальный вектор — это такой вектор, который является перпендикулярным (ортогональным) к данной плоскости или прямой.

Для этого из нашего очаровательного примера системы уравнений необходимо взять коэффициенты из уравнений. В итоге для 1-ой плоскости вектор-нормаль будет выглядеть как $(A_1; B_1; C_1)$, а для второй как $(A_2; B_2; C_2)$.

Теперь необходимо перемножить оба вектора и получить их произведение, здесь $(i, j, k)$ - координаты единичного вектора.

$|\overline \cdot \overline| = \overline \cdot (B_1 \cdot C_2 – C_1 \cdot B_2) - \overline \cdot (A_1 \cdot C_2 – A_2 \cdot C_1) + \overline \cdot (A_1 \cdot B_2 – A_2 \cdot B_1)$

Следующим этапом выполняем поиск координат точки, возлежащей на искомой прямой.

Для выполнения этого наиболее "сложного" пункта необходимо выбрать одну наиболее нравящуюся вам координату $x, y$ или $z$ и вместо неё подставить в систему уравнений, описывающую плоскости, нулевое значение.

Составьте каноническое уравнение прямой, получаемой из системы уравнений, описывающей пару пересечённых плоскостей:

$\begin 2x – y + 3z + 4 = 0 \\ x + 5y – 3z – 7 = 0 \\ \end$

Найдём направляющий вектор, для этого сначала запишем вектора нормалей плоскостей:

Ну а сейчас пора вычислить сам направляющий вектор:

Найдём точку, находящуюся на нашей прямой, тут всё просто, приравняем $y$ к нулю и внедрим в нашу систему уравнений:

$\begin 2x + 3z + 4 = 0 \\ x – 3z – 7 = 0 \\ \end$

Решение вышеприведённой системы уравнений будет: $x = 1, z = -2$, то есть координаты точки, возлежащей на нашей прямой, будут $(1; 0; -2)$.

Подставим все полученные нами цифры и получим следующее уравнение:

Составление канонического уравнения прямой по координатам двух точек

На практике это очень распространённая и любимая во многих вузах и других учебных заведениях задача — нужно найти уравнение прямой в пространстве, проходящей через 2 точки. Примем заранее, что эти две точки не обладают одинаковыми $x, y, z$.

Для того чтобы написать уравнение прямой в пространстве, проходящей через 2 точки, воспользуйтесь координатами ваших точек и внедрите их в следующее уравнение:

Это уравнение можно вывести из параметрического уравнения прямой.

Допустим, у нас есть две точки с координатами $(x_1; y_1; z_1)$, и для второй $(x_2; y_2; z_2)$.

Найти направляющий вектор для изучаемой прямой при наличии пары точек несложно, вектор с координатами $(x_2 – y_1; y_2 – y_2;z_2 – z_2)$ и будет желаемой частью результата.

Придумаем точку, находящуюся на нашей прямой, пусть она будет обладать координатами $(x_1;y_1;z_1)$.

Помещаем обнаруженные нами координаты вектора и точки в каноничное уравнение прямой в пространстве и получим уравнение прямой, проходящей через 2 точки.

Если же необходимо выразить именно параметрические уравнения из координат двух точек, через которые проведена некая одна прямая, то тут тоже всё довольно просто и без неожиданностей:

$\begin x = x_1 + (x_2 - x_1) \cdot λ \\ y = y_1 + (y_2 - y_1)\cdot λ \\ z = z_1 + (z_2 - z_1) \cdot λ \\ \end$

1. Прямую в пространстве можно задать как линию пересечения двух плоскостей, если нормали у них не параллельны:

– общее уравнение.

2. – канонические уравнения.

3. – параметрические уравнения.

Геометрический смысл букв, входящих в канонические и параметрические уравнения: – координаты текущей точки прямой, – координаты фиксированной точки прямой, – координаты направляющего вектора прямой.

Заметим, что в каждой точке пространственной прямой можно провести бесчисленное множество векторов, перпендикулярных к ней, не параллельных между собой. Поэтому задание нормали к прямой не определяет ее положения в пространстве. Чтобы составить канонические и параметрические уравнения прямой в пространстве, нужна фиксированная точка прямой и ее направляющий вектор.

Расстояние от точки до прямой находится по формуле

, (16)

Где – радиус-вектор точки , – радиус-вектор фиксированной точки прямой и – ее направляющий вектор.

Расстояние между двумя прямыми и , ( не параллелен ) вычисляется по формуле

. (17)

Условие пересечения прямых: . Если прямые скрещиваются, то .

Чтобы перейти от общего уравнения к каноническим или параметрическим, надо найти фиксированную точку и направляющий вектор. Так как прямая задана как линия пересечения двух плоскостей, то все точки прямой принадлежат обеим плоскостям. Получаем два уравнения на три неизвестные. Одну из координат, например , полагаем равной любому числу (проще всего нулю) и, решая систему двух уравнений с двумя неизвестными, находим остальные две координаты.

Если система окажется несовместной при выбранном (на прямой нет точки с такой аппликатой), то либо полагаем равному другому числу, либо полагаем или .

Направляющий вектор находим как векторное произведение и , так как и .

Пример 1. Написать канонические и параметрические уравнения прямой

Решение. Положим , тогда получим откуда находим , . Фиксированная точка . , , , . Канонические уравнения: . Обозначая , получим параметрические уравнения: , , .

Пример 2. Найти уравнение прямой, проходящей через точки и .

Решение. В качестве фиксированной точки прямой можно взять любую из точек и . Направляющим вектором служит любой вектор, параллельный прямой (в частности, расположенный на самой прямой), поэтому . Запишем уравнения .

Пример 3. Вычислить расстояние от точки до прямой . Часто вызывает недоумение число нуль, стоящее в знаменателе (одна из координат направляющего вектора равна нулю). В этом случае полагают равным нулю соответствующий числитель, в данном случае – уравнение одной из плоскостей.

Решение. Из уравнения прямой берем фиксированную точку и . Воспользуемся формулой , где , , , . . .

Пример 4. Указать значения , при которых прямые и пересекаются.

Решение. Из уравнений прямых находим , , , , . Условие пересечения прямых запишем в координатной форме , откуда .

Пример 5. Проверить, лежат ли прямые и в одной плоскости.

Решение. Из уравнения прямых находим , , , , тогда . Если прямые лежат в одной плоскости, то векторы компланарны, значит . Для проверки этого условия запишем его в координатной форме:

, следовательно прямые не лежат в одной плоскости, т. е. скрещиваются.

Пример 6. Составить уравнение прямой, которая проходит через точку и пересекает две прямые и .

Решение. Из условия находим , , , , тогда , .

Обозначим – направляющий вектор искомой прямой. Будем искать уравнение в виде . Запишем условие пересечения двух прямых: и , откуда для нахождения получаем систему

Так как число уравнений меньше числа неизвестных, то разделим уравнения, например, на : Решая эту систему относительно неизвестных и , найдем , или .

Итак, . Канонические уравнения искомой прямой: .

Пример 7. Найти точку пересечения прямой с плоскостью .

Решение. Можно было бы от канонических уравнений прямой перейти к общему: или а затем найти точку пересечения трех плоскостей. Рациональней другой путь. Перейдем к параметрическим уравнениям прямой: , , . Подставим эти выражения для в уравнение плоскости: , откуда . Тогда , , .

1. Найти уравнение прямой, проходящей через точку параллельно прямой .

Ответ: .

2. Написать параметрические уравнения прямой взяв в качестве фиксированной точки .

Ответ: .

3. Найти расстояние между прямыми и .

4. Найти угол между прямыми и .

Ответ: .

5. Найти проекцию начала координат на прямую .

Ответ: .

6. Найти уравнение перпендикуляра, опущенного из точки на прямую В ответе укажите координаты направляющего вектора.

Ответ: .

7. Составить уравнение проекции прямой на плоскость . В ответе укажите координаты направляющего вектора.

Ответ: .

8. Прямая пересекает прямую , оси и и параллельна плоскости . Найти длину отрезка искомой прямой между точками пересечения ее с осями координат.

9. Выяснить взаимное расположение прямой и плоскости . Если они не параллельны, найти их точку пересечения.

Ответ: .

10. Найти точку , симметричную точке относительно прямой, проходящей через точки и .

Ответ: .

Читайте также: