Умножение матриц как сделать

Добавил пользователь Алексей Ф.
Обновлено: 19.09.2024

Пример 1.8. Даны матрицы
Вычислить произведения .

Решение. Все матрицы квадратные второго порядка. Следовательно, все произведения будут квадратными матрицами того же порядка. Используя правило умножения, получаем

Замечание 1.2. Непосредственным вычислением можно доказать основное свойство единичной матрицы :

Пример 1.9. Найти произведения

Решение. 1) Произведением

Оба произведения — это квадратные матрицы одного и того же порядка, но .

Результаты умножения совпадают, т.е. .

Свойства умножения матриц

Пусть — произвольные матрицы, для которых определены операции умножения и сложения, записанные в левых частях следующих равенств. Тогда определены операции, указанные в правых частях, и справедливы равенства:

1. ; (ассоциативность умножения матриц)

2. ; (дистрибутивность умножения)

3. ; (дистрибутивность умножения)

Пример 1.10. Продемонстрировать справедливость свойств 1, 2, если

Решение. Проверим свойство 1: .

Проверим свойство 2: .

1. В общем случае умножение матриц не является коммутативным. Произведение зависит от перестановки множителей, т.е . Во-первых, размеры матриц и будут также квадратными матрицами того же порядка. Даже при этих условиях умножение матриц не коммутативно (см. пример 1.8 и 1.9,6, где ). С другой стороны, в примере 1.8 и , а в примере 1.9, в . Перестановочными могут быть только квадратные матрицы одного и того же порядка. В частности, например, можно показать, что диагональные матрицы одного и того же порядка перестановочны.

2. Для любой квадратной матрицы справедливы следующие равенства

Другими словами, единичная матрица перестановочна с любой квадратной матрицей того же порядка.

3. Для любой матрицы 4. Множество квадратных матриц одного и того же порядка 5. Заметим, что сумма и произведение диагональных (верхних треугольных, нижних треугольных) матриц одного и того же порядка являются диагональными (верхними треугольными, нижними треугольными) матрицами. Следовательно, операции сложения и умножения матриц определены на множествах диагональных (верхних треугольных, нижних треугольных) матриц одного и того же порядка. Поэтому каждое из указанных множеств является кольцом с единицей, причем кольцо диагональных матриц коммутативное.

Пример 1.11. Найти матрицы, перестановочные с матрицей .

Решение. Для выполнения равенства и удовлетворяет равенству

После умножения получаем в левой и правой частях равенства квадратные матрицы второго порядка:

Записывая равенство соответствующих элементов этих матриц, получаем систему уравнений

Из первого уравнения следует, что , где — параметры, принимающие любые действительные значения.

Умножение матриц на столбцы и строки единичной матрицы

Рассмотрим два типа преобразований квадратной матрицы -го порядка при помощи умножения на строки и столбцы единичной матрицы.

Обозначим j-й столбец и i-ю строку единичной матрицы n-го порядка через и соответственно:

1. Найдем произведения

Как видим, в результате умножения матрицы выделяется j-й столбец матрицы получаем i-ю строку матрицы матрицы

Пример 1.12. Даны матрицы

Решение. Перемножая матрицы, получаем:

В результате умножений из данной матрицы .

2. Умножая справа матрицу , а затем на строку получаем квадратную матрицу n-го порядка, в которой все элементы равны нулю, за исключением элементов j-го столбца, который совпадает с j-м столбцом матрицы

При помощи умножения на строки и столбцы можно, например, заменить j-й столбец матрицы

Пример 1.13. Даны матрицы, вычислить .

Решение. Выполняя действия, получаем:

В результате 2-й столбец матрицы Математический форум (помощь с решением задач, обсуждение вопросов по математике).

в этом пошаговом руководстве показано, как использовать C++ AMP для ускорения выполнения умножения матрицы. Представлены два алгоритма: один — без мозаичного заполнения и один с мозаичным заполнением.

Предварительные требования

Перед началом работы

убедитесь, что вы используете не менее Windows 7 или Windows Server 2008 R2.

Создание проекта

инструкции по созданию нового проекта зависят от установленной версии Visual Studio. Чтобы ознакомиться с документацией по предпочтительной версии Visual Studio, используйте селектор Версия. Он находится в верхней части оглавления на этой странице.

Создание проекта в Visual Studio

В строке меню выберите Файл Создать Проект, чтобы открыть диалоговое окно Создание проекта.

В верхней части диалогового окна задайте для параметра Язык значение C++, для параметра Платформа значение Windows, а для Типа проекта — Консоль.

в отфильтрованном списке типов проектов выберите пустой Project а затем нажмите кнопку далее. На следующей странице введите матриксмултипли в поле имя , чтобы указать имя проекта, и при необходимости укажите расположение проекта.

В Обозреватель решенийоткройте контекстное меню исходных файлови выберите команду добавить новый элемент.

В диалоговом окне Добавление нового элемента выберите файл C++ (. cpp), введите Матриксмултипли. cpp в поле имя , а затем нажмите кнопку Добавить .

создание проекта в Visual Studio 2017 или 2015

в строке меню Visual Studio выберите файл создать Project.

В разделе установленные на панели шаблоны выберите Visual C++.

выберите пустое Project, введите матриксмултипли в поле имя , а затем нажмите кнопку ок .

В Обозреватель решенийоткройте контекстное меню исходных файлови выберите команду добавить новый элемент.

Умножение без мозаичного заполнения

В этом разделе мы рассмотрим умножение двух матриц, A и B, которые определены следующим образом:

A — это матрица размером 3 на 2, а B — матрица размером 2 на 3. Результатом умножения A на B является следующая матрица с 3 по 3. Продукт вычисляется путем умножения строк объекта на столбцы элемента B по элементу.

Умножение без использования C++ AMP

Откройте Матриксмултипли. cpp и используйте следующий код, чтобы заменить существующий код.

Алгоритм является простой реализацией определения умножения матрицы. Он не использует параллельные или потоки алгоритмы для сокращения времени вычисления.

В строке меню выберите файл сохранить все.

Нажмите клавишу F5 , чтобы начать отладку, и убедитесь, что выходные данные верны.

Нажмите клавишу Ввод , чтобы выйти из приложения.

Умножение с помощью C++ AMP

В Матриксмултипли. cpp добавьте следующий код перед main методом.

Код AMP напоминает код, отличный от AMP. Вызов parallel_for_each запускает один поток для каждого элемента в product.extent и заменяет for циклы для строк и столбцов. Значение ячейки в строке и столбце доступно в idx . Доступ к элементам объекта можно получить с array_view помощью [] оператора и переменной индекса либо () оператора и переменных строки и столбца. В примере демонстрируются оба метода. array_view::synchronize Метод копирует значения product переменной обратно в productMatrix переменную.

Добавьте следующие include инструкции и using в начало матриксмултипли. cpp.

Измените main метод, чтобы вызвать MultiplyWithAMP метод.

Нажмите сочетание клавиш CTRL F5 , чтобы начать отладку и убедиться, что выходные данные верны.

Нажмите клавишу пробел , чтобы выйти из приложения.

Умножение с помощью мозаичного заполнения

Мозаичное заполнение — это методика разделения данных на подмножества одинакового размера, которые называются плитками. При использовании мозаичного заполнения изменились три вещи.

Можно создавать tile_static переменные. Доступ к данным в tile_static пространстве может выполняться в несколько раз быстрее, чем доступ к данным в глобальном пространстве. Экземпляр tile_static переменной создается для каждой плитки, а все потоки в плитке имеют доступ к переменной. Основным преимуществом мозаичного заполнения является повышение производительности из-за tile_static доступа.

Можно вызвать метод tile_barrier:: wait , чтобы останавливаются все потоки в одной плитке в указанной строке кода. Нельзя гарантировать порядок, в котором будут выполняться потоки, только тогда, когда все потоки в одной плитке будут прекращаться на вызове tile_barrier::wait до продолжения выполнения.

У вас есть доступ к индексу потока относительно всего array_view объекта и индекса, относящихся к плитке. С помощью локального индекса можно упростить чтение и отладку кода.

Чтобы воспользоваться преимуществами мозаичного умножения матрицы, алгоритм должен секционировать матрицу на плитках, а затем копировать данные плитки в tile_static переменные для ускорения доступа. В этом примере матрица секционирована на подматрицы одинакового размера. Продукт можно найти, умножив подматрицы. В этом примере используются две матрицы и их продукты:

Матрицы разделены на четыре матрицы 2x2, которые определяются следующим образом:

Теперь продукт A и B можно записать и вычислить следующим образом:

Так как матрицы a h являются матрицами 2x2, все продукты и их суммы также являются матрицами 2x2. Также следует убедиться, что продукт A и B является матрицей 4x4, как и ожидалось. Чтобы быстро проверить алгоритм, Вычислите значение элемента в первой строке первого столбца продукта. В этом примере это значение элемента в первой строке и первом столбце ae + bg . Необходимо вычислить только первый столбец, первая строка ae и bg для каждого термина. Это значение для параметра ae равно (1 * 1) + (2 * 5) = 11 . Значение bg равно (3 * 1) + (4 * 5) = 23 . Конечное значение — 11 + 23 = 34 , что является правильным.

Для реализации этого алгоритма код:

Использует tiled_extent объект вместо extent объекта в parallel_for_each вызове.

Использует tiled_index объект вместо index объекта в parallel_for_each вызове.

Создает tile_static переменные для хранения подматриц.

Использует tile_barrier::wait метод, чтобы прерывать потоки для вычисления продуктов подматриц.

Умножение с помощью AMP и мозаичного заполнения

В Матриксмултипли. cpp добавьте следующий код перед main методом.

Этот пример значительно отличается от примера без мозаичного заполнения. В коде используются следующие концептуальные шаги:

Скопируйте элементы мозаики [0, 0] a в locA . Скопируйте элементы мозаики [0, 0] b в locB . Обратите внимание, что product происходит мозаичное заполнение, a а не и b . Таким образом, глобальные индексы используются для доступа к a, b , и product . Вызов метода tile_barrier::wait является обязательным. Он останавливает все потоки в плитке до тех пор, locA пока locB не будут заполнены и.

Умножьте locA и locB помещайте результаты в product .

Скопируйте элементы мозаики [0, 1] a в locA . Скопируйте элементы мозаики [1, 0] b в locB .

Умножьте locA и locB добавьте их в результаты, которые уже находятся в product .

Умножение плитки [0, 0] завершено.

Повторите эти четыре плитки. Индексирование для плиток не предусмотрено, и потоки могут выполняться в любом порядке. По мере выполнения каждого потока tile_static переменные создаются для каждой плитки соответствующим образом и вызывают tile_barrier::wait Управление потоком программы.

При тщательном анализе алгоритма Обратите внимание, что каждая подматрица загружается в tile_static память дважды. Эта перенаправление данных занимает некоторое время. Однако после того, как данные находятся в tile_static памяти, доступ к данным будет выполняться гораздо быстрее. Поскольку вычисление продуктов требует многократного доступа к значениям в подматрицах, существует общий выигрыш в производительности. Для каждого алгоритма требуется экспериментирование, чтобы найти оптимальный алгоритм и размер плитки.

В примерах, отличных от AMP и не являющихся плитками, доступ к каждому элементу A и B осуществляется четыре раза из глобальной памяти для вычисления продукта. В примере плитки доступ к каждому элементу осуществляется дважды из глобальной памяти и четыре раза из tile_static памяти. Это не является значительной приростом производительности. Однако если A и B были 1024x1024 матрицы и размер плитки был 16, то производительность будет значительно увеличена. В этом случае каждый элемент копируется в tile_static память 16 раз и доступ к нему осуществляется из tile_static памяти 1024 раз.

Измените метод Main, чтобы вызвать MultiplyWithTiling метод, как показано ниже.

Нажмите сочетание клавиш CTRL F5 , чтобы начать отладку и убедиться, что выходные данные верны.

На данной странице калькулятор поможет умножить две матрицы онлайн с подробным решением. Для расчета задайте целые или десятичные числа.

Вычисление матриц

Умножаются матрицы, у которых число столбцов матрицы А равняется числу строк матрицы В.

Умножение матриц

Что бы умножить матрицу A_ij на матрицу B_ij, нужно сложить произведения i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B.
C_ij = A_i1 · B_1j + A_i2 · B_2j + . + A_in · B_nj

Пример

$<\left(\begin1 & 2 \\ 2 & 4 \end\right) \cdot \left(\begin1 & 3 \\ 4 & 7 \end\right) =\left(\begin9 & 17 \\ 18 & 34 \end\right)>$

Линейная алгебра

Как умножить матрицу на матрицу и как умножить матрицу на число — обсуждаем на примерах с решением и объяснением. Произведение матрицы на число и произведение матрицы на матрицу просто и на примерах.

Умножение матрицы на число

, то есть, если

$A = \begin a_& a_ & a_ & . & a_\\ a_& a_ & a_ & . & a_ \\ \ldots & \ldots & \ldots & . & \ldots \\ a_& a_ & a_ & . & a_ \end$
,

$kA = \begin ka_& ka_ & ka_ & . & ka_\\ ka_& ka_ & ka_ & . & ka_ \\ \ldots & \ldots & \ldots & . & \ldots \\ ka_& ka_ & ka_ & . & ka_ \end$
.

Рассмотрим умножение матрицы на число на примере:

Пример 1

$A= \begin Умножьте матрицу 2 & 5\\ 7& -3 \end$
на число .

Решение: Чтобы умножить матрицу на число 2, нужно умножить на это число каждый элемент матрицы. Итак, получим:

$2A= \begin 2\cdot 2 & 2 \cdot 5\\ 2 \cdot 7& 2 \cdot (-3) \end= \begin 4 & 10\\ 14& -6 \end$
.

Пример 2

$A= \begin Найдите матрицу, противоположную матрицу 2 & 5 & -1 \\ 7& -3 & 5 \\ 8 & 6 & 0 \end$
.

Решение: Чтобы найти противоположную матрицу надо умножить исходную матрицу на .

$-A= \begin -2 & -5 & 1 \\ -7& 3 & -5 \\ -8 & -6 & 0 \end$
.

Пример 3

Даны матрицы 1 & 4 & -3 \\ 8& -2 & 8 \\ 9 & 2 & -3 \end" width="150" height="64" />
и -1 & 3 & -7 \\ 9 & 2 & 6 \\ 4 & -2 & 3 \end" width="165" height="64" />
. Вычислите .

$2A-B= \begin 2 & 8 & -6 \\ 16& -4 & 16 \\ 18 & 4 & -6 \end - \begin -1 & 3 & -7 \\ 9 & 2 & 6 \\ 4 & -2 & 3 \end= \begin 3 & 5 & 1 \\ 7 & -6 & 10 \\ 14 &6 & -9 \end$
.

Умножение матрицы на матрицу

Чтобы умножить матрицу на матрицу необходимо умножать последовательно каждый элемент каждой строки первой матрицы на каждый элемент каждого столбца второй матрицы и сумму этих произведений записать в соответствующем элементе матрицы-произведения.

Давайте рассмотрим умножение матрицы на матрицу на примере. Пусть нам нужно умножить две квадратные матрицы и .

a_ & a_ & a_ \\ a_& a_ & a_ \\ a_ & a_ & a_ \end" width="168" height="64" />
, b_ & b_ & b_ \\ b_& b_ & b_ \\ b_ & b_ & b_ \end" width="163" height="64" />

Умножением матрицы на матрицу называется матрица:

$C= \begin a_b_+a_b_+a_b_ & a_b_+a_b_+a_b_ & a_b_+a_b_+a_b_ \\ a_b_+a_b_+a_b_& a_b_+a_b_+a_b_ & a_b_+a_b_+a_b_ \\ a_b_+a_b_+a_b_ & a_b_+a_b_+a_b_ & a_b_+a_b_+a_b_ \end =\begin c_ & c_ & c_ \\ c_& c_ & c_ \\ c_ & c_ & c_ \end$
.

Таким образом, получаем:

надо все элементы -й строки матрицы A умножить на соответствующие элементы -го столбца матрицы B и полученные произведения сложить.

Рассмотрим умножение матрицы на матрицу на примерах.

Пример 1

Найдите произведение матриц:

2 & 5\\ 7& -3 \end" width="108" height="43" />
и -3 & 4\\ 8& 5 \end" width="109" height="43" />
.

$AB= \begin Находим произведение матриц 2 \cdot (-3)+5 \cdot 8 & 2 \cdot 4+5 \cdot 5\\ 7 \cdot (-3)+(-3) \cdot 8& (-3) \cdot 4+ (-3) \cdot 5 \end= \begin 34 & 33\\ -45 & -27 \end$
.

Таким образом, для прямоугольных матриц правило умножения матрицы на матрицу такое же, как и для квадратных матриц.

Пример 2

Найдите произведение AB, если

0 & -1 & 2 \\ 2& 1 & 1 \\ 3 & 0 & 1 \\ 3 & 7 & 1 \end" width="136" height="85" />
, 3 & 1 \\ 2& 1 \\ 1 & 0 \end" width="98" height="64" />
.

Мы смогли найти произведение AB, однако, мы не сможем найти произведение BA.

Правила умножения матриц

Не все матрицы можно перемножать, для того, чтобы произведение матриц было возможным, необходимо соблюдение следующих правил:

Умножение матрицы A на матрицу B имеет смысл только в том случае, когда число столбцов матрицы A равно числу строк матрицы B.

В результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк в первой матрице, и столько столбцов, сколько столбцов во второй матрице.

Свойства умножения матриц

Рассмотрим умножение двух матриц 2 & -1\\ 1& 3 \end" width="108" height="43" />
и 3 & 1\\ 1& -1 \end" width="109" height="43" />
. Найдем произведение и произведение , а затем сравним эти произведения.

$AB=\begin 2 & -1\\ 1& 3 \end \begin 3 & 1\\ 1& -1 \end=\begin 2 \cdot 3+(-1) \cdot 1 & 2 \cdot 1+(-1) \cdot (-1)\\ 1 \cdot 3+3 \cdot 1& 1 \cdot 1+3 \cdot (-1) \end= \begin 5 &3\\ 6& -2 \end$
;

$BA=\begin 3 & 1\\ 1& -1 \end\begin 2 & -1\\ 1& 3 \end=\begin 3 \cdot 2+1 \cdot 1 & 3 \cdot (-1)+1 \cdot 3\\ 1 \cdot 2+(-1) \cdot 1& 1 \cdot (-1)+(-1) \cdot 3 \end= \begin 7 &0\\ 1& -4 \end$
.

Очевидно, что . Таким образом, для произведения матриц переместительный закон не выполняется. Однако, два других закона умножения, сочетательный закон и распределительный закон выполняются:

— сочетательный закон умножения,

— распределительный закон.

Из школьного курса математики известно, что произведение двух отличных от нуля чисел равно отличному от нуля числу. Однако при умножении двух ненулевых матриц можно получить нулевую матрицу, смотрите:

Возьмем две матрицы 1 & 1\\ 1& 1 \end" width="94" height="43" />
и 1 & -1\\ -1& 1 \end" width="123" height="43" />
. Найдем произведение этих матриц:

$AB=\begin 1 & 1\\ 1& 1 \end \begin 1 & -1\\ -1& 1 \end=\begin 1 \cdot 1+1 \cdot (-1) & 1 \cdot (-1)+1 \cdot 1\\ 1 \cdot 1+1 \cdot (-1)& 1 \cdot (-1)+1 \cdot 1 \end= \begin 0 &0\\ 0& 0 \end$

Умножение матриц – это одна из самых распространенных операций с матрицами. Матрица, которая получается после умножения, называется произведением матриц.

Произведением матрицы A_m_×_n на матрицу B_n_×_k будет матрица C_m_×_k такая, что элемент матрицы C, находящийся в i-ой строке и j-ом столбце, то есть элемент c_ij равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-ого столбца матрицы B.

Процесс умножения матриц возможен только в случае, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример:
Можно ли умножить матрицу на матрицу ?

m = n, значит, умножать данные матрицы можно.

Если же матрицы поменять местами, то, при таких матрицах, умножение уже не будет возможно.

m ≠ n, таким образом, выполнять умножение нельзя:

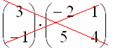
Довольно часто можно встретить задания с подвохом, когда ученику предлагается умножить матрицы, умножение которых заведомо невозможно.

Обратите внимание, что иногда можно умножать матрицы и так, и так. К примеру, для матриц, и возможно как умножение MN, так и умножение NM.

Операция умножения матриц.

Операция умножения матриц – это не очень сложное действие. Умножение матриц лучше понимать на конкретных примерах, т.к. только определение может сильно запутать.

Начнем с самого простого примера:

Необходимо умножить на . Первым делом приведем формулу для данного случая:

– здесь хорошо прослеживается закономерность.

Далее более сложный пример:

Умножить на .

Формула для этого случая: .

Умножение матриц и результат:

В результате получена т.н. нулевая матрица.

Теперь рассмотрим примеры умножения матриц третьего порядка:

Умножить на .

Формула очень похожа на прошлые:

Решение матрицы: .

Умножение матрицы на число.

Умножение матрицы на число – это тоже самое умножение матриц, только вместо второй матрицы берется простое число. Как можно догадаться, такое умножение выполнять гораздо проще.

Пример умножения матрицы на число:

Тут все понятно – для того, чтобы умножить матрицу на число, необходимо каждый элемент матрицы последовательно умножить на указанное число. В данном случае – на 3.

Еще один полезный пример:

– умножение матрицы на дробное число.

Первым делом покажем то, чего делать не надо:

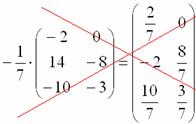
При умножении матрицы на дробное число не нужно вносить дробь в матрицу, так как это в первую очередь только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем.

И, тем более, не нужно делить каждый элемент матрицы на -7:

Что стоит сделать в данном случае – это внести минус в матрицу:

Если бы у вас был пример, когда все элементы матрицы делились бы на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

В данном примере можно и нужно умножить все элементы матрицы на ½, т.к. каждый элемент матрицы делится на 2 без остатка.

Читайте также: