Можно ли уменьшить невыгодный момент инерции путем изменения спортивной техники и как это сделать

Обновлено: 06.07.2024

Аннотация научной статьи по механике и машиностроению, автор научной работы — Козеев Арсений Александрович, Разяпов Махмут Магдутович, Масалимов Ильгам Хамбалович, Нафиков Марат Закиевич, Ямалетдинов Марсель Мусавирович

Целью данной работы является проведение экспериментальных исследований и разработка маховика с переменным моментом инерции . Исследование по определению момента инерции проводилось по известной методике НАМИ с помощью стенда на трёхнитевом подвесе. Прототипом выбран маховик автомобиля ГАЗ-3307, дополненный диском с направляющими для грузов. Результаты испытаний показали, что изменение радиуса инерции за счёт смещения груза повышает эффективность работы двигателя. При меньшем радиусе инерции облегчается запуск двигателя за счёт снижения нагрузки на коленчатом валу, а при большом помогает преодолевать кратковременные перегрузки за счёт дополнительного момента инерции . По результатам испытаний разработан универсальный маховик с переменным моментом инерции . Представлены принципиальная схема его работы и трёхмерная модель сборочного чертежа. Дано описание принципа работы маховика . В зависимости от частоты вращения коленчатого вала и приходящегося на него нагрузки, подпружиненные грузики посредством электронного блока управления занимают соответствующее положение на маховике . Разработанный маховик с переменным моментом инерции позволяет повысить тягово-скоростные свойства и топливную экономичность наземного транспорта .

DEVELOPING A FLYWHEEL WITH A VARIABLE INERTIA MOMENT FOR LAND MEANS OF TRANSPORT

The purpose of this work is to carry out experimental studies and develop a flywheel with variable moment of inertia . In order to fulfill the objective, investigations to determine the moment of inertia were carried out according to the known method of SAMI using a bench on a three-line suspension. The prototype is the flywheel of the GAZ-3307 car, supplemented by a disc with guides for cargo. The results of the tests showed that changing the radius of inertia due to load displacement increases the efficiency of the engine. Thus, with a smaller radius of inertia, engine start-up is facilitated due to reduction of load on the crankshaft, and with a large one helps to overcome short-term overloads due to additional moment of inertia . According to the results of the tests, a universal flywheel with a variable moment of inertia has been developed. A schematic diagram of its operation and a three-dimensional model of the assembly drawing are provided. The principle of flywheel operation is as follows. Depending on speed of crankshaft rotation and load on it, spring-loaded weights by means of electronic control unit occupy corresponding position on flywheel . In conclusion, it can be noted that the developed flywheel with variable moment of inertia allows to increase traction-speed properties and fuel economy of ground transport.

Разработка маховика с переменным моментом инерции для наземного транспорта

А.А. Козеев, к.т.н., М.М. Разяпов, к.т.н., И.Х. Масалимов, к.т.н., М.З. Нафиков, д.т.н., ММ. Ямалетдинов, к.т.н., ФГБОУ ВО Башкирский ГАУ

Наземный транспорт в современном мире в большинстве случаев используется для выполнения перевозки грузов. С увеличением транспортного потока режим работы двигателя транспортных средств переходит в неустановившийся, который характеризуется частым изменением частоты вращения коленчатого вала и передаваемого крутящего момента. Это в свою очередь способствует возникновению динамических нагрузок в двигателе и в трансмиссии, приводит к ухудшению тягово-скоростных свойств и топливной экономичности [1 - 4].

В связи с этим появляется необходимость разработки маховика с переменным моментом инерции, который помогает двигателю преодолевать дополнительные нагрузки, что приводит к улучшению тягово-скоростных свойств.

При запуске двигателя подвижные элементы будут располагаться на минимальном радиусе за счёт упругости пружины и электромагнитов, тем самым облегчая пуск, снижая нагрузку на коленчатый вал и стартер. При увеличении угловой скорости коленчатого вала установленные подпружиненные подвижные элементы от возникающих центробежных сил будут стремиться к наибольшему радиусу, создавая в результате дополнительный момент инерции. Это необходимо при перегрузках двигателя для преодоления дополнительных сил сопротивления, при этом будет использоваться кинетическая энергия подпружиненных подвижных элементов [5 - 10].

Целью данной работы является проведение экспериментальных исследований и разработка маховика с переменным моментом инерции.

Материал и методы исследования. Основным параметром маховика является момент инерции. Для проведения лабораторных исследований по определению момента инерции и оценки влияния расположения подвижных элементов на маховике используется лабораторный стенд трёхнитевого подвеса, предложенный нами.

Принцип данной методики состоит в том, что испытуемая вращающаяся деталь наземного транспорта устанавливается на трёхнитевом подвесе, а затем определяется период её свободных колебаний относительно оси вращения (рис. 1).

Испытания проводились на маховике автомобиля ГАЗ-3307 (рис. 2), дополненного диском с перемещаемыми грузами.

Диск с грузами выполнен из круга перфорированной сетки, идентичный по размерам маховика автомобиля ГАЗ-3307. В качестве перемещаемого груза использован шестигранник. Для удобства перемещения грузов были вырезаны продольные направляющие. Диапазон изменения радиуса расположения груза составил 65 - 110 мм.

В итоге мы получили установку для проведения испытаний по замеру момента инерции (рис. 3).

Испытания и расчёты проводили по известной методике:

8,444а 2t 2шд g -10"3 L

где а - расстояние между нитями подвеса, 0,16 м; ^ - время колебаний, с; тд - масса детали в сборе с установкой, 29,75 кг;

g - ускорение свободного падения, 9,81 м/с2; Ь - длина нити подвеса, 3,2 м. Были получены результаты: 1) без использования грузов:

м _ 8,444-0,162 -4,9592 -27,85-9,81 10-3 = ' 3,2

Рис. 1 - Схема трёхнитевого подвеса:

1 - металлический диск, 2 - нить подвеса, 3 -крепление нити, 4 - отверстие крепления детали, 5 - ось вращения (ось угловых колебаний)

2) минимальный радиус расположения грузов 60 мм:

м _ 8,444-0,162-4,8872-29,85-9,81-10~3 = ' 3,2

3) радиус расположения грузов 110 мм:

м _ 8,444-0,162 -4,9292 -29,85-9,81-Ю"3 '' 3,2 "

4) максимальный радиус расположения грузов 145 мм:

м _ 8,444-0,162 -5,2052 -29,85-9,81-Ю"3 = '' 3,2

Результаты исследования. Проведённые расчёты позволили построить график зависимости коэффициента учёта вращающихся масс от радиуса расположения грузов относительно оси вращения (рис. 4).

По полученным расчётам и приведённому графику можно сделать вывод о нелинейной зави-

симости коэффициента учёта вращающихся масс от радиуса расположения груза. При наименьшем расположении грузов происходит уменьшение момента инерции, что в свою очередь облегчает запуск двигателя. По мере увеличения радиуса расположения грузов увеличивается момент инерции и коэффициент учёта вращающихся масс. Данное явление положительно повлияет на работу двигателя при работе с перепадами нагрузок, так как дополнительный запас момента инерции поможет их преодолеть.

Проделанные испытания дали возможность разработки маховика с переменным моментом инерции (рис. 5).

Маховик с переменным моментом инерции работает следующим образом. При раскручивании коленчатого вала установленные подпружиненные подвижные элементы от возникающих центробежных сил будут стремиться к наибольшему радиусу, тем самым создавая дополнительный момент инерции. Данное явление необходимо при перегрузках двигателя, для преодоления которых будет использоваться момент инерции подпружиненных подвижных

Рис. 2 - Предложенная конструкция маховика:

А - маховик; Б - диск с грузами

Ш/ ¿77/ У/ 'шжт ушШт

Рис. 4 - График зависимости коэффициента учёта вращающихся масс от изменения радиуса расположения грузов

Рис. 5 - Маховик с переменным моментом инерции:

А - принципиальная схема, Б - 3Б-модель; 1 - пружины; 2 - подпружиненные подвижные элементы; 3 - электромагниты; 4 - корпус маховика; 5 - датчик скорости; 6 - обмотка приемник; 7 - обмотка передатчик; 8 - электронный блок управления; 9 - генератор

элементов. При запуске двигателя подвижные элементы будут располагаться на минимальном радиусе за счёт упругости пружины и электромагнитов, тем самым облегчая пуск, снижая нагрузку на коленчатый вал и стартер. При работающем двигателе возможно изменение положения подвижных элементов. Электронный блок управления посредством датчика оборотов коленчатого вала будет определять, в какой момент необходимо изменение момента инерции, тем самым перемещать подпружиненные элементы за счёт воздействия магнитного поля, образующующегося от обмотки передатчика и обмотки приемника. Технология основана на магнетизме и электромагнетизме и базируется на ряде простых принципов работы.

Вывод. Проведённые испытания позволили модернизировать существующие маховики наземного транспорта с установкой дополнительных подпружиненных грузов с возможностью изменения их расположения относительно оси вращения. Данные изменения позволили улучшить тягово-скоростные свойства и топливную экономичность автомобиля или трактора.

1. Габитов И.И., Неговора А.В. Передовые технологии технического обслуживания и ремонта топливной аппаратуры дизелей // Вестник Башкирского государственного аграрного университета. 2015. № 3 (35). С. 40 - 44.

2. Неговора А.В., Байрамов Р.А. Совершенствование системы предпусковой подготовки автотракторных дизелей в условиях низких температур // Тракторы и сельскохозяйственные машины. 2008. № 5. С. 49 - 50.

3. Модуль для поэлементного диагностирования топливоподающей системы дизелей / А.В. Неговора, А. А. Козеев, М.М. Габдрахимов [и др.] // Механизация и электрификация сельского хозяйства. 2010. № 3. С. 13 - 14.

4. Неговора А.В., Низамутдинов А.И., Хакимов Р.Т. Специализированное устройство для исследования закона подачи топлива в системах питания дизелей // Технико-технологические проблемы сервиса. 2014. № 3 (29). С. 11 -13.

5. Неговора А.В., Махиянов УА., Ахметов А.Ф. Совершенствование способов диагностирования топливоподающих систем дизелей с электронным управлением // Известия Международной академии аграрного образования. 2012. Т. 1. № 14. С. 260 -265.

6. Габитов И.И., Неговора А.В. Обеспечение работоспособности топливоподающих систем дизелей путем индивидуальной корректировки базовых характеристик управления топливоподачей // Российская сельскохозяйственная наука. 2016. № 4. С. 84 - 88.

7. Нигматуллин Ш.Ф., Габдрахимов М.М., Валиев М.М. Диагностирование насоса топливной системы Common Rail на основе параметрической идентификации колебаний давления в аккумуляторе // Вестник Башкирского государственного аграрного университета. 2011. № 4. С. 64 - 66.

8. Нигматуллин Ш.Ф., Габдрахимов М.М. Стенд для испытания компонентов топливных систем типа Common Rail // Известия Международной академии аграрного образования . 2013. № 17. С. 200 - 202.

9. Карачурин Б.Ш., Нигматуллин Ш.Ф., Костарев К.В. Модернизация стенда втс-101 по проверке форсунок топливоподающих систем типа Common Rail // Инженерное обеспечение в АПК: научный сборник / Министерство сельского хозяйства Российской Федерации, Министерство образования Республики Башкортостан, Башкирский государственный аграрный университет, механический факультет. Уфа, 2015. С. 58 - 62.

10. Нигматуллин Ш.Ф., Костарев К.В., Карачурин Б.Ш. Исследование влияния температуры технологической жидкости на цикловую подачу электрогидроуправляемой форсунки // Вестник Башкирского государственного аграрного университета. 2015. № 3 (35). С. 69 - 71.

Ответ. С первого взгляда вращение даже нагляднее демонстрирует свойства инерции, чем прямолинейное движение. Вращающийся в вакууме на магнитной подвеске маховик может двигаться годами, так как внешние воздействия на него сведены к минимуму [11, 12].

Однако, строго говоря, движение по инерции может быть только равномерным и прямолинейным. Значит, вращения по инерции в принятой нами ньютоновой механике быть не может. Но ведь твердое массивное тело сохраняет состояние покоя или равномерного вращения, пока его не выведет из этого состояния момент внешних сил. Стало быть, фактически и здесь имеет место явление инерции, хотя и отличное от классического случая. Что же общего и в чем различие между инерцией вращения и инерцией при прямолинейном движении?

Инертность массивной точки (тела) зависит только от ее массы. Масса является мерой инертности тела при поступательном, в том числе и прямолинейном, движении. Значит, при таком движении на инерцию не влияет распределение масс в теле, и это тело можно смело принять за материальную (массивную) точку. Масса этой точки равна массе тела, а расположена точка в центре масс или центре инерции тела. Если же вращать вокруг вертикальной оси Ж стержень с насаженными на него массивными грузами (рис. 3.1), то можно заметить, что пока грузы

Рис. 3.1. Схема изменения момента инерции тела

находятся близ центра, раскрутить стержень легко. Но если грузы раздвинуть, то раскрутить стержень станет труднее, хотя масса его не изменилась. Стало быть, инертность тела при вращении зависит не только от массы, но в большей степени от распределения этой массы относительно оси вращения. Мерой инертности тела при вращении является осевой момент инерции I, равный сумме произведений масс т всех частиц тела на квадраты их расстояний h от оси вращения:

Осевой момент инерции играет при вращательном движении ту же роль, что и масса при поступательном (прямолинейном), и таким образом, он является мерой инертности (инерции) тела при вращательном движении.

Таким образом, механические явления в покоящейся и вращающейся системах будут протекать по-разному, не говоря уже о том, что если тело достаточно сильно раскрутить, то его разорвет на части из-за возникших в нем напряжений.

Еще одно отличие состоит в том, что прямолинейное равномерное движение и покой эквивалентны, а вращение, даже с постоянной угловой скоростью, может быть четко отграничено не только от покоя, но и от вращения с другой угловой скоростью.

3.2. Вопрос. Можно ли сформулировать законы инерции вращения аналогично первому закону Ньютона?

Почему же абсолютно твердое тело, а не любое? Потому, что у нетвердого тела из-за вынужденных деформаций при вращении изменится момент инерции, а это равносильно изменению массы точки для первого закона Ньютона.

3.3. Вопрос. Земля и Луна вращаются вокруг общего центра масс. Действуют ли на эти небесные тела центробежные силы?

Ответ. Представление, что при вращении материальных точек и тел вокруг оси или неподвижной точки на них должны действовать центробежные (т.е. направленные от центра вращения) силы, является обывательским заблуждением.

Например, и на Землю, и на Луну действуют силы тяготения, направленные друг к другу, а следовательно, к центру вращения (рис. 3.2). Каких-либо сил, направленных от центра, здесь вообще нет. Чтобы тела, движущиеся по инерции, т.е. равномерно и прямолинейно, свернули с этого пути и стали двигаться по кривым, на них должны подействовать центростремительные, т.е. направленные к центру вращения, силы. Такими являются силы тяготения.

В случае, если вращается точка А, привязанная к опоре О на гибкой невесомой связи — нити (рис. 3.3, а), то, пренебрегая силой тяжести (допустим, опыт поставлен в невесомости),

Рис. 3.3. Силы, действующие на тела во вращающейся системе:

а — силы, действующие на вращающуюся по окружности точку А и опору О; б — силы, действующие на связь можно сказать, что на эту точку также действует центростремительная сила F_n. На саму же нить, как на связь, со стороны точки А действует направленная от центра реакция а со

стороны опоры О — сила R₂ = F₄ (рис. 3.3, б). На опору О действует сила Fц, направленная от центра. На нить действует уравновешенная система сил, которая не может влиять на движение точки А.

3.4. Вопрос. Почему при быстром вращении тела оно испытывает механические напряжения и может даже разрушиться, ведь никакое другое тело с ним не контактирует, на него не действуют никакие силовые поля и т.д.?

Ответ. Действительно, если опыт по вращению, допустим, металлического кольца поставить в невесомости и в вакууме, то с этим телом не будет взаимодействовать никакое другое тело, даже воздух. Разогнать это кольцо можно вращающимся электромагнитным полем (например, возникающим в статоре асинхронного электродвигателя), особенно если кольцо стальное. После окончания разгона свободно вращающееся с угловой скоростью щ кольцо будет обладать кинетической энергией Е:

и будет растягиваться механическим напряжением а:

где I — осевой момент инерции кольца; р — плотность материала кольца; v — линейная скорость кольца.

Чем же вызвано это напряжение? Выше мы видели, что на связь — нить (см. рис. 3.3, а, б) действуют растягивающие усилия, вызываемые точкой А, вращающейся вокруг опоры О. Ведь именно связь, действуя на точку А центростремительной силой F_n, постоянно сворачивает ее с естественного прямолинейного пути. В этом случае масса (точка А) и связь (невесомая нить) четко выделены. Но если точку А устранить, вместо нити взять массивное тело — стержень или цепь — и вращать его вокруг точки О, то картина усложнится.

В таких случаях, когда связь сама обладает массой, удобно представить ее в виде невесомой связи (нити), нагруженной отдельными массивными точками (рис. 3.4). Если число точек невелико, центростремительные силы, действующие на эти точки, легко определить: в точке 1 это Е_ц1, в точке 2 — сумма двух сил (Е_ц1 + Е_ц2), а в точке 3 она максимальна — сумма трех сил (*m + F_n 2 + Ец₃). Отсюда легко перейти к случаю, когда масса распределена по длине связи равномерно.

Рис. 3.4. Невесомая связь — нить, нагруженная точечными

Так и с вращающимся кольцом — если представить, что его заменяет многоугольник из невесомых нитей с помещенными в вершинах углов грузами т (рис. 3.5, а), то выделив один из грузов (рис. 3.5, б), можем определить силы F_CB, действующие на груз (их реакции действуют на нить):

где F_u = m(o 2 R или mv 2 /R, что следует из формулы (2.4).

Распределив грузы т по нити равномерно, получим массивное кольцо плотностью л, обладающее прочностью связи (рис. 3.6).

Рис. 3.5. Схематичное представление вращающегося кольца:

а — замкнутый вращающийся многоугольник с помещенными в вершинах углов точечными массами; б — силы, действующие на отдельный груз

Рис. 3.6. Схема для определения напряжений во вращающемся кольце

Для простоты вычислений отбросим нижнюю половину кольца и обозначим через F растягивающие усилия, действующие с его стороны на верхнее полукольцо. Учитывая, что центр масс верхнего полукольца С расположен на расстоянии 2R/n вверх от центра О, нормальное ускорение этого центра масс:

Записываем второй закон Ньютона в проекции на направление нормального ускорения:

Учитывая, что напряжения а = F/S, где S — площадь сечения кольца, масса полукольца М = npRS, и что линейная скорость v = соR, записываем с учетом (3.6):

Таким образом, получаем формулу (3.3).

Следовательно, вращающееся кольцо будет растягиваться с силой F и напряжениями у даже без контакта с каким-нибудь другим телом. Аналогичным образом возникают напряжения во вращающихся телах любой конфигурации, например, в движущихся гибких массивных замкнутых связях — ремнях, цепях, а также маховиках — накопителях кинетической энергии.

3.5. Вопрос. Как накопить во вращающемся маховике наибольшую кинетическую энергию?

Ответ. Кинетическая энергия вращающегося тонкого кольца массой т, как и для прямолинейно движущейся массы, пропорциональна квадрату его линейной (окружной) скорости:

Ведь и в том и в другом случаях масса m движется с одной и той же скоростью v. Разница лишь в том, что в случае прямолинейного движения в движущемся теле не возникает никаких напряжений, а при вращении кольца (как и ремня, цепи, любой плоской массивной замкнутой связи), в нем возникают напряжения, не зависящие от радиуса кольца и определяемые формулой (3.3). Следовательно, в прямолинейно движущейся массе можно беспредельно (в рамках классической механики) повышать скорость и кинетическую энергию. Во вращающейся же массе, в данном случае кольце, мы жестко лимитированы прочностью материала, причем и кинетическая энергия и напряжения в материале пропорциональны квадрату окружной скорости.

А если это будет не кольцо, а тело иной формы? Удастся ли при той же прочности материала накопить большую кинетическую энергию? Для анализа этого вопроса удобнее всего выразить энергию и прочность через удельные показатели — удельную энергоемкость е = Е/т и удельную прочность х = ст/р. Тогда для маховика в виде вращающегося кольца

Для маховиков других форм коэффициент к будет принимать другие значения. Например, для диска с очень маленьким центральным отверстием он будет равен 0,3; для диска вообще без отверстия — 0,6. Самой лучшей формой маховика для накопления кинетической энергии является диск равной прочности. Такую форму имеют, например, диски паровых и газовых турбин — толстые в центре и тонкие на периферии.

3.6. Вопрос. Можно ли создать энергоемкий маховик с переменным моментом инерции?

Ответ. Устройство, изображенное на рис. 3.1, в принципе позволяет как накапливать кинетическую энергию, так и изменять момент инерции. Но из-за низкой прочности такая конструкция будет иметь ничтожную удельную энергоемкость. Если изготовить маховик из резины, то в процессе вращения его момент инерции будет расти тем более, чем больше угловая скорость маховика. К кинетической энергии при этом добавится потенциальная, накопленная при растяжении резины.

При постоянном кинетическом моменте маховика можно увеличивать момент инерции за счет уменьшения угловой скорости и наоборот. Пример — человек с гантелями в руках на так называемой платформе Жуковского — диске, закрепленном на стойке на подшипниках (рис. 3.7, а, б).

Рис. 3.7. Человек на платформе (скамье) Жуковского:

а — с разведенными в сторону руками и большим моментом инерции;

6 — со сдвинутыми к центру руками и минимальным моментом инерции

Если человек, стоя на этой платформе с разведенными в стороны руками, вращается (рис. 3.7, а), то сведя руки с гантелями к центру (рис. 3.7, б), он снижает свой момент инерции, за счет чего значительно увеличивает угловую скорость. Маховики с регулируемым переменным моментом инерции могли бы обеспечить практически любую угловую скорость, необходимую рабочему органу машины, например, колесам автомобиля.

3.7. Вопрос. К каким последствиям может привести замена инерциальной системы отсчета на неинерциальную, например, вращающуюся?

Ответ. Каждому относительному движению тела во вращающейся системе отсчета можно поставить в соответствие движение точно такого же тела относительно инерциальной системы координат. Но для такого соответствия надо воспроизвести не только те реальные силы, которые действовали на исходное тело, но и добавить новые силы, соответствующие эйлеровым силам инерции в относительном движении исходного тела. Эйлеровы силы инерции здесь определяются как реальные силы, действующие на тело, в предположении, что подвижная система отсчета условно принимается за неподвижную. Например, если поворачивающий автобус мы примем за неподвижный, то нам придется считать реальными центробежные силы, действующие на повороте.

3.8. Вопрос. Можно ли определить эйлеровы силы инерции не формально, а исходя из физической сути явлений?

Таким образом, эйлеровы силы инерции равны тем физическим силам, которые следует добавить к исходным физическим силам, чтобы в точности воспроизвести относительное движение какого- либо тела как движение абсолютное, т.е. в инерциальной системе отсчета.

3.9. Вопрос. Если кориолисовы силы инерции нереальны, как они могут вызвать подмывание берегов рек? Что такое гироскопический эффект?

Ответ. Подмывание берегов рек можно качественно объяснить и без использования подвижной системы отсчета, эйлеровых сил инерции и других предположений.

На Южном полушарии все происходит наоборот. Если взглянуть на Землю со стороны Южного полюса, то вращается она уже в другом направлении. Все, у кого есть глобус, могут проверить это. Вот вам и закон Бэра, названный так в честь российского естествоиспытателя Карла Бэра (1792—1876), подметившего эту особенность рек.

А тут уже недалеко и до объяснения гироскопического эффекта вообще. Продолжим нашу реку дальше и опишем ею замкнутый круг на поверхности Земли. При этом заметим, что вся северная часть реки, находящаяся в Северном полушарии, будет стремиться направо, а вся южная часть — налево. Вот и все объяснение гироскопического эффекта, который считается едва ли не труднейшим в теоретической механике!

Итак, наша река — это огромное кольцо или маховик, вращающийся в том же направлении, что и течение реки. Если при этом поворачивать этот маховик в направлении вращения Земли, то вся северная его часть будет отклоняться вправо, а южная — влево (рис. 3.8). Иначе говоря, маховик будет поворачиваться так, чтобы его вращение совпало с направлением вращения Земли! Это и является качественным проявлением гироскопического эффекта.

3.10. Вопрос. Говорят, что гироскопический эффект удерживает велосипед от падения. Так ли это?

Ответ. Приходится много читать о том, что устойчивость велосипеда достигается благодаря гироскопическому эффекту его колес. Между тем — это явное преувеличение, и вот почему.

Гироскопический эффект — это возникновение момента при попытке принудительного поворота оси вращающегося тела. Но величину гироскопического момента мы пока не определяли. При поворачивании оси велосипедного колеса этот момент равен произведению момента инерции колеса на угловые скорости его вращения и поворота оси (вынужденной прецессии). Для простоты решим, что масса колеса 2 кг, радиус его

0,25 м и, стало быть, момент инерции, примерно равный произведению массы на квадрат радиуса, равен 0,125 кг-м 2 . Велосипедист спокойно маневрирует уже на скорости 1 м/с, и колесо при этом вращается с угловой скоростью 4 рад/с. Угловая скорость поворота оси колеса раз в 20 меньше и равна примерно 0,2 рад/с. В результате получаем гироскопический момент, равный 0,1 Н • м. Это то же самое, что гирьку в 1 кг подвесить на конец гвоздя, торчащего из стены всего на 1 см. Вряд ли такой ничтожный момент может что-либо изменить в движении велосипеда.

В то же время едущий велосипедист, свернув всего на 10 см от прямой, если не наклонится в сторону поворота, создаст опрокидывающий момент, равный его весу плюс примерно полвеса велосипеда, умноженные на 0,1 м, что достигает порядка 100 Н • м. Этот момент в тысячу раз больше, чем гироскопический момент! Вот таким образом, наклоняясь к центру поворота, велосипедист сохраняет устойчивость.

3.11. Вопрос. Если выстрелить из пушки вертикально вверх, то упадет ли снаряд снова в ствол пушки?

Ответ. Эта задача не давала покоя механикам XIX века. Конечно же, снаряд упадет обратно в ствол, если все происходит в абсолютной системе отсчета. А в реальной жизни, то есть на вращающейся Земле, все будет не так. Обычно эту задачу рассматривают с переходом на вращающуюся систему отсчета, что сильно усложняет ее, по крайней мере в математическом отношении. Давайте здесь попробуем рассмотреть лишь качественную сторону этой задачи в инерциальной системе отсчета.

Допустим, на широте Москвы массивная точка падает в вакууме с вышки высотой 100 м. Земля вращается с запада на восток, и точка эта имела в момент падения окружную скорость большую, чем поверхность Земли, так как дальше отстояла от ее центра. Падая, точка сохраняет свою окружную скорость, и соприкоснется она с Землей, сместившись в сторону превышения скорости, т.е. на восток. Расчет показывает, что это смещение невелико — всего 1,2 см.

А теперь выстрелим точечным снарядом вертикально вверх. В момент выстрела — на поверхности Земли — окружная скорость точки меньше, чем на высоте. Поэтому, поднимаясь вверх, точка будет отклоняться на запад. Особенно большое время точка проведет в верхней зоне своего полета, так как вертикальная скорость там мала, поэтому и путь, пройденный на запад, будет достаточно велик. На обратном пути точка тоже будет отклоняться на запад, правда теперь все медленнее и медленнее. Таким образом, она упадет западнее жерла пушки.

Кстати, наклонив ствол пушки чуть-чуть на восток, можно, в принципе, добиться того, чтобы снаряд, падая, коснулся снова жерла пушки; но реально, особенно с учетом влияния атмосферы, это сделать невозможно — задача эта сугубо теоретического плана.

Конечно же, весь расчет можно было бы провести точно, причем без привлечения фиктивных кориолисовых сил. Но большинство специалистов-механиков считает, что помещая нашу пушку в относительную вращающуюся систему координат и вводя фиктивные кориолисовы силы, можно выполнить расчет короче и проще. Если даже это и так, то не потерять бы главного — ощущения реальности происходящего, что в физике играет не последнюю роль!

Это – вторая лекция из цикла, посвященного экспертному анализу движения автомобилей в ДТП. Вспомните, как фигуристка, обладая некоторым количеством вращательного движения, прижимает руки к телу и ее вращение ускоряется, так как ее момент инерции стал меньше, а количество движения неизменно. Для расчета же вращения автомобиля в плоскости необходимо знать его момент инерции относительно вертикальной оси, проходящей через центр тяжести. В автомобильных справочниках, как правило, нет величины моментов инерции. Поэтому эксперты не мудрят — если им надо, они рассчитывают момент инерции упрощенно, как для плиты тех же габаритных размеров. Но правильно ли это? Знать ответ на этот вопрос полезно как адвокатам, так и экспертам.

Момент инерции – это физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг оси. Момент инерции подобен массе тела, которая тоже является мерой его инертности, но в поступательном движении. Момент инерции характеризуется распределением масс в теле. Он равен сумме произведений элементарных масс, составляющих тело, на квадрат их расстояний до оси вращения.

Если массу автомобиля достаточно просто рассчитать, зная массы всех его деталей, или измерить на весах, то произвести расчет момента инерции автомобиля гораздо сложнее из-за сложной геометрической формы его деталей. Поэтому момент инерции автомобиля проще измерить на специальном стенде, работающего по принципу крутильного маятника, как, например, показано на рисунке выше.

Вычисление момента инерции автомобиля

Для простейших вычислений с использованием ньютоновской механики полагается, что масса транспортного средства сосредоточена в его центре тяжести. Это предположение правильно для центральных или для близких к нему ударов, когда линия силы удара проходит через центр тяжести автомобиля или близко к нему. Когда столкновение автомобилей имеют эксцентричный характер, с последующим вращением в результате удара, что является наиболее распространенным случаем ДТП, то простая модель центрального удара является неадекватной, и в таких случаях должно быть учтено распределение массы автомобиля относительно его центра тяжести.

Сопротивление объекта вращению прямо зависит от массы объекта и расположения этой массы по отношению к центру вращения, или от его момента инерции. Идеализированное транспортное средство может рассматриваться твердая однородная плита массойm (в килограммах) с длиной a (в метрах) и шириной b (в метрах). Тогда момент инерции этой однородной плиты относительно вертикальной оси, проходящей через ее центр тяжести, находится по формуле (в кг*м 2 ):

Реальное транспортное средство – это не однородная плита. Оно имеет такие концентрированные массы, как, например, двигатель, трансмиссия, элементы подвески. Поэтому фактический момент инерции автомобиля всегда меньше момента инерции однородной плиты тех же геометрических размеров и массы.

Из специальной литературы известно несколько попыток предложить универсальный способ расчета момента инерции автомобиля в виде соотношения, связывающего массу автомобиля, его геометрические размеры и расположение центра тяжести. Однако все подобные исследования были произведены до 1997 года, и, в связи с изменяющимися стандартами и тенденциями развития автомобилестроения, результаты таких исследований быстро устаревают.

С целью получения актуальной информации из базы данных DSD, входящей в специальную компьютерную программу PC-Crash, была произведена выборка 73 наиболее распространенных в России моделей автомобилей 2009-2014 годов. Выборка производилась произвольно, для каждого производителя в выборку не включались автомобили сходных по габаритам и массе моделей. В таблицах ниже для каждой модели из выборки указаны наименование, масса снаряженного автомобиля, габаритная длина, габаритная ширина, расчетное значение момента инерции по приведенной выше формуле для однородной плиты, фактическое значение момента инерции, превышение расчетного значения момента инерции над фактическим в процентах.

Как видно из представленной выборки, расчетное значение момента инерции превышает его фактическое от 16% до 34%. Следовательно, можно ожидать, что аппроксимация линейной зависимостью значения фактического момента инерции как функции расчетного значения момента инерции даст приемлемые для использования результаты.

На графике на рисунке ниже ось абсцисс – расчетный момент инерции, ось ординат –фактический момент инерции, точками показаны фактические данные из таблиц выше. Методом наименьших квадратов была получена линейная зависимость фактического значения момента инерции от расчетного значения в виде

которая показана на рисунке ниже в виде сплошной прямой. Пунктиром показаны линии превышения момента инерции на плюс-минус 10%.

Видно, что на графике выше все фактические точки лежат в приемлемой области возможной погрешности значения момента инерции плюс-минус 10%.

Таким образом, с погрешностью не более 10% момент инерции автомобиля относительно вертикальной оси, проходящей через его центр тяжести, может быть определен по графику выше или рассчитан по формуле

где m – масса снаряженного автомобиля, a – длина автомобиля, b – ширина автомобиля.

Для учета загрузки автомобиля водителем, пассажирами и грузом, согласно теореме Гюйгенса, для каждого из них можно прибавить к полученной величине момента инерции снаряженного автомобиля значение произведения массы каждого объекта на квадрат расстояния от центра тяжести этого объекта до центра тяжести автомобиля.

Резюме

Таким образом, данная лекция полезна не только для экспертов по ДТП, но и для адвокатов, осуществляющих защиту по ст.264 УК РФ. Адвокатам — тем, что можно легко проверить исходные данные эксперта, чтобы он не "накормил севрюжиной с хреном" как адвоката, так и его клиента, тихо увеличив в десяток-другой раз момент инерции одного из автомобилей, участвовавших в ДТП.

Литература:

1. MacInnis, D., Cliff, W., and Ising, K., A Comparison of Moment of Inertia Estimation Techniques for Vehicle Dynamics Simulation. // SAE Technical Paper 970951, 1997, doi:10.4271/970951.

Одним из фундаментальных свойств физических тел является момент инерции. Люди с ним сталкиваются в повседневной жизни при езде на велосипеде или автомобиле, запуске различных механизмов, игре с мячом, катании на карусели и т. д. Изучают характеристику на уроках физики и сопромата. Знание этого параметра важно и в механике, особенно при нахождении силы, которая может привести тело к вращению.

Основные понятия и суть

Инерция — это способность тела сохранять приданную ей скорость движения при отсутствии какого-либо внешнего воздействия. Например, во время езды на общественном транспорте всем приходится держаться за поручни. Если этого не сделать, то при изменении скорости движения транспортного средства существует большая вероятность упасть вперёд или назад. Другими словами, возникает какая-то сила, влияющая на пассажира. Когда её действие заканчивается, движение человека всё равно продолжается.

Это свойство и описывается понятием инертность. Раньше изучали это явление известные учёные Галилей, Ньютон, Мах. В соответствии с их исследованиями было установлено классическое правило момента вращения, физический смысл которого заключается в распределении массы в теле, определяемой суммой произведения простейшей массы на расстояние до начального множества в квадрате. Классическая формула, описывающая характеристику, выглядит следующим образом: Ja = Σmi*r 2 j. В ней:

mi — масса в точке;
rj — расстояние от точки до координаты.

То есть момент — это скалярная величина, являющаяся мерой инертности. В качестве единицы измерения по международной системе принято использовать произведение килограмма на квадратный метр (кг*м²). Обозначают параметр латинской буквой I или J. При умножении момента инерции на угловое ускорение можно определить сумму моментов всех сил, приложенных к телу: M = I * E. Фактически это уравнение является аналогом второго закона Ньютона.

М — это момент силы, оказывающий вращательное движение и воздействующий на ускорение тела, а E — угловое ускорение. Мера инертности тела отличается от массы тем, что вторая проявляется, когда его необходимо разогнать, а первая — при его раскручивании.

Вычисление параметра

Характеристика инерции тел зависит от их количественных показателей и формы. Для того чтобы найти характеристику, можно рассмотреть вращение материальной точки, находящейся на невесомой штанге, имеющей длину r и массу m. Для такой ситуации формулу момента инерции можно записать: I = m*r 2 . Длина r представляет собой радиус кольца, по которому происходит вращение объекта по оси. Таким образом, рассматриваемый момент зависит не только от массы тела, но и геометрических характеристик.

Любое тело можно описать совокупностью материальных точек. Для понятия процесса лучше всего рассмотреть простой пример. Пусть имеется невесомый цилиндр, способный вращаться по радиусу Rc. На него намотана верёвка, к которой приложена сила F. На цилиндр будут насаживаться тела с различной формой. Если известны его радиус и сила, с которой происходит раскручивание, то справедливо будет записать следующее выражение: M = F*Rc.

Допустим, на цилиндр помещены два тела. Одно имеет массу m1 и радиус вращения r1, а другое — m2 и r2. Используя основное уравнение динамики вращательного движения для первого тела с угловым ускорением ƹ1, момент силы можно определить как M1 = I1 * ƹ1. Соответственно, для второго предмета сила будет определяться по формуле: M1 = I2 * ƹ2.

Если эти два тела жёстко скрепить между собой, то они буду представлять собой составные части одного предмета, поэтому их угловые ускорения станут одинаковы (ƹ1 + ƹ2 = ƹ), а требующийся момент M станет равный сумме M1 + M2. Подставив значения, получим равенство M = I1*ƹ + I2*ƹ. Выражение можно упростить до вида M = ƹ (I1+I2). То есть нужный момент для тела, состоящего из совокупности точек, будет равен произведению суммы моментов инерции на угловое ускорение обоих тел.

Из сказанного можно сделать вывод, что момент инерции всего тела равен сумме моментов составных частей. Другим словами, он обладает свойством аддитивности. Используя это, можно составить алгоритм расчёта для любой формы.

Методика решения

Существует универсальный алгоритм, подходящий для расчёта параметра прямоугольника, треугольника, круга или другой фигуры произвольной формы. Допустим, есть сложное тело с заданной осью вращения. Необходимо найти момент его вращения. Для того чтобы решить поставленную задачу, используются два принципа:

Аддитивность — свойство, обозначающее, что величина целого значения определяется суммой соответствующих ему частей.
Формула нахождения момента для материальной точки I = m*r 2 .

Всё тело можно разделить на мельчайшие частички, которые представляют собой материальные точки. Номера этих кусков обозначают в виде i. Масса произвольной части будет определяться как дельта mi. Пусть этот кусок находится на расстоянии ri от оси вращения O. Для этой части момент вращения находится с помощью выражения Ii = Δ mi*ri 2 . Учитывая аддитивность, общий момент будет равен I = Σ Δ mi*ri 2 , где i принимает значение от 1 до n.

Эта формула является приближённой, так как точность зависит от массы частей и размера. Если кусочки, на которые разбивается тело, большие, считать их материальными точками нельзя. Чем мельче части, тем точнее будет результат. В соответствии с математическим анализом такие задачи решаются с помощью интегрирования. Понимая физический смысл момента инерции, можно отметить следующие зависимости:

прямая пропорциональность массе;
соответствие квадрату размера;
изменение с учетом оси вращения.

Роль последнего пункта огромна. Например, если рассмотреть два момента вращения велосипедной спицы диаметром 2 мм и длиной 30 сантиметров, то можно увидеть зависимость от выбранной оси поворота.

Относительно вертикальной оси вращение обозначим I1, горизонтальной — I2. Подставив в формулы выражения, используемые для расчётов, можно получить отношение I1/I2 = (m*l2/12) / ((m*d2/8). После его упрощения будет верна запись I1/ I2 = (2/3)*(l/d)2. В итоге получится ответ 15000. Получается, если спицу будут закручивать с одинаковым моментом вокруг вертикальной оси и горизонтальной, то в первом случае она станет крутиться в 15 тыс. раз быстрее.

Моменты простейших объектов

Проведение интегрирования — довольно трудная операция, предполагающая хорошее знание высшей математики. Существует таблица, в которой собраны вычисления инерции для простейших геометрических фигур. При взятии сведений из неё важно обращать внимание на то, относительно какой оси приводится момент вращения объекта. Характеристика инерции для наиболее используемых объектов в физике имеет следующий вид:

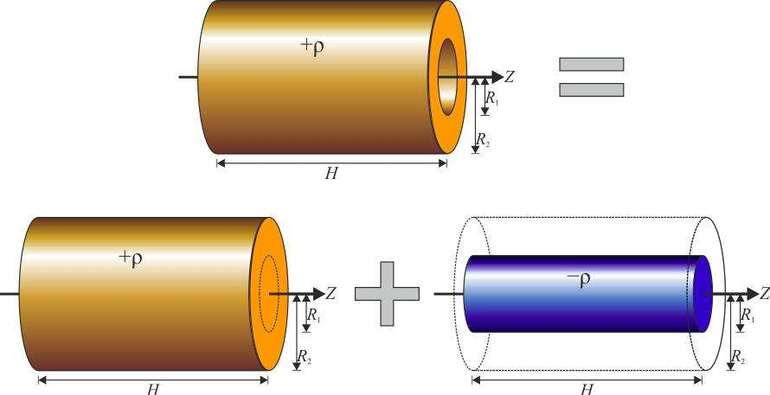
Кольцо. Предположив, что точка имеет симметричное значение с противоположной стороны оси, можно утверждать, что формула не изменится. Если же точку распределить по плоскости перпендикулярной оси, то получится кольцо. Оно будет иметь такую же массу с кусками, находящимися на одинаковом расстоянии от центра r. Вычисление момента относительно оси вращения выполняют по той же формуле, что и для материальной точки: I = m * r 2 .
Тонкостенный цилиндр. Нарисовав такую фигуру и указав на ней ось вращения, массу и радиус, несложно будет увидеть, что формула для нахождения момента будет аналогична кольцу.
Диск. Вращение его происходит относительно оси, проходящей через его центр. Учитывая, что масса однородного диска распределена по всей его площади, то момент его будет меньше, чем у кольца. Проведённые расчёты показали, что момент диска будет меньше в два раза. Таким образом, формула выглядит как I = m*r 2 / 2.
Сплошной цилиндр. Получают такую фигуру простым распределением массы сплошного диска вдоль оси. По аналогии с кольцом расчёт его характеристики инерции будет совпадать с однородным диском.
Шар. Момент проходящей оси через центр тяжести равен удвоенному произведению m*r2, разделенному на 5: I = (m*r2) * 2/5.
Сфера. Такой объект отличается от шара лишь тем, что внутри он полый. Направление вращения оси происходит через центр. Значение параметра для неё будет больше, чем шара, так как масса собрана не статически в одном месте, а размещена по всей поверхности. Расчёты показывают, что найти момент можно по формуле I =2*m*r2 /3.
Стержень. Момент вращения проходит через центр вдоль оси, перпендикулярной стержню: I = (1/12) * m*L2. L — длина стержня.

При использовании этих формул необходимо учитывать, что единицей измерения момента инерции является кг* м², поэтому при расчёте величины следует приводить значения к этим единицам.

Теорема Гюйгенса — Штейнера

Теорема была названа в честь двух математиков, давших формулировку определению характеристики параллельных осей. Например, пусть имеется объект произвольной формы, центробежная сила которого известна. Используя формулу Штейнера, можно вычислить момент тела относительно любой оси параллельной линии, проходящей через середину фигуры. В своём выводе учёные опирались на две формулы:

Вычисления координаты центра масс: X = (m1*x1 + m2*x2+…+Mi*Xi) / (m1+m2+…+Mi) = (Σ Δ mi*ri 2 )/ m.
Универсального расчёта инерции любого тела: I = Σ Δ mi*ri 2 .

Обозначив центр произвольной оси буквой O, а один из множества кусков — Δm, можно воспользоваться универсальной формулой. Сначала необходимо определить квадрат расстояния до оси вращения ri. Для этого через центр проведём ось Oц, а расстояние между O и Oц обозначим как d.

Указанные значения нужно выразить через координаты кусочка. Для этого строится ось абсциссы, проходящая через Oц, и ординаты — O. При таком выборе направления начала координат x центр масс равняется d, а у — нулю. Фактически получится прямоугольный треугольник. Воспользовавшись теоремой Пифагора, можно записать: I = Σ Δ mi* (xi2 + yi2).

В результате можно отметить, что момент в точке O будет прямо пропорционален расстоянию между Δ m и центром. Это и есть главный вектор на чертеже. Для его обозначения вводится длина r'.

Находится ri' 2 по формулам для прямоугольного треугольника, в котором один катет равняется yi, а другой — xi — Oц. Значение ri' совпадает с длиной гипотенузы. Таким образом, ri' 2 = (xi — Oц) 2 + yi 2 . Подставив полученное равенство в формулу нахождения параметра момента в центре, можно получить следующую формулу: Io = Σ Δ mi* ((xi — Oц) 2 + yi 2 ). После ряда подстановок и упрощения выражения в итоге получится равенство Io = I + m*x i 2 — 2*m*xi 2 = I — m*xi 2 .

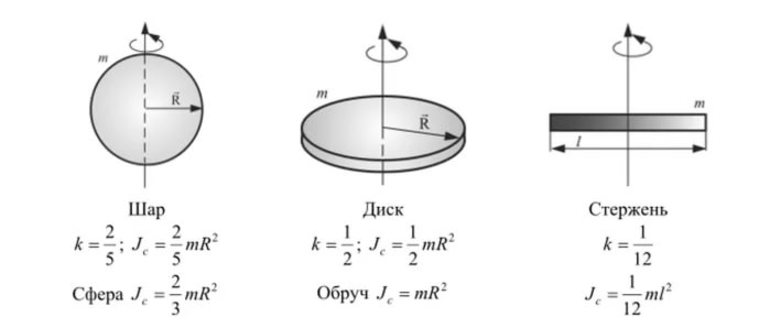
Другими словами, теорема определяет, что характеристика инерции тела относительно любой оси находится как сумма моментов относительно параллельной оси, пересекающей центр масс, и произведению массы тела на квадрат расстояния между осями. Сопротивлением вращению пренебрегают.

Пример задачи

Допустим, есть монета с массой m и радиусом r. Вращение происходит вокруг оси, распложенной по касательной. Необходимо найти момент вращения.

Для этого нужно знать характеристику прямой, пересекающей центр монеты Io. Решение будет определяться суммой Io и расстоянием от центра до касательной, которая равняется диаметру монеты: I = Io + md 2 . Фактически задача состоит в нахождении Io. Определяется этот параметр согласно теореме о взаимно перпендикулярных осях.

Момент вращения относительно диска определяется с помощью выражения I1 = m* d 2 / 2. Для решения задачи она будет выглядеть Io = m* d 2 / 4. Подставив все данные, получим: I = (1m*d2 / 4) + (md)2 = 5*m*d2 /4.

Читайте также: