Как сделать функцию непрерывной

Добавил пользователь Алексей Ф.
Обновлено: 18.09.2024

Непрерывные функции образуют основной класс функций, с которыми оперирует математический анализ. Представление о непрерывной функции можно получить, если сказать, что график ее непрерывен, т.е. его можно начертить, не отрывая карандаша от бумаги.

Непрерывная функция математически выражает одно свойство, с которым нам приходится часто встречаться на практике, заключающееся в том, что малому приращению независимой переменной соответствует малое же приращение зависимой от нее переменной (функции). Прекрасными примерами непрерывной функции могут служить различные законы движения тел , выражающие зависимости пути устанавливает между ними определенную непрерывную связь, характеризующуюся тем, что малому приращению времени соответствует малое же приращение пути.

К абстракции непрерывности человек пришел, наблюдая окружающие его, так называемые сплошные среды — твердые, жидкие или газообразные, например металлы, воду, воздух. На самом деле, как теперь хорошо известно, всякая физическая среда представляет собой скопление большого числа отделенных друг от друга движущихся частиц. Однако эти частицы и расстояния между ними настолько малы по сравнению с объемами сред, с которыми приходится иметь дело в макроскопических физических явлениях, что многие такие явления можно достаточно хорошо изучать, если считать приближенно массу изучаемой среды без всяких просветов, непрерывно распределенной в занятом ею пространстве. На таком допущении базируются многие физические дисциплины, например гидродинамика, аэродинамика, теория упругости. Математическое понятие непрерывности играет, естественно, в этих дисциплинах, как и во многих других, большую роль.

Рассмотрим какую-либо функцию и вполне определенное значение независимой переменной . Если наша функция отражает некоторый непрерывный процесс, то значениям должны соответствовать значения функции мало отличающиеся от значения в точке . Таким образом, если приращение независимой переменной мало, то должно быть малым также и соответствующее приращение функции. Иными словами, если приращение независимой переменной стремится к нулю, то приращение функции должно, в свою очередь, стремиться к нулю, что может быть записано следующим образом:

Это соотношение и является математическим определением непрерывности функции в точке .

Функция называется непрерывной в точке , если выполняется равенство (1).

Дадим еще такое определение:

Функция называется непрерывной для всех значений, принадлежащих к данному отрезку, если она непрерывна в каждой точке этого отрезка, т.е. в каждой такой точке выполняется равенство (1).

Таким образом, для того чтобы ввести математическое определение свойства функции, заключающегося в том, что график ее есть непрерывная (в обычном понимании этого термина) кривая, появилась необходимость определить сначала локальное, местное свойство непрерывности (непрерывность в точке ), а затем на этой основе определить непрерывность функции на целом отрезке.

Приведенное определение, впервые указанное в начале прошлого столетия Коши, является общепринятым в современном математическом анализе. Проверка на многочисленных конкретных примерах показала, что это определение хорошо соответствует сложившемуся у нас практическому представлению о непрерывной функции, например представлению о непрерывном графике.

В качестве примеров непрерывных функций могут служить известные из школьной математики элементарные функции . Все перечисленные функции непрерывны на отрезках изменения , при которых функция, стоящая в знаменателе, обращается в нуль. Результат деления представляет собой тогда разрывную в точке функцию.

Определение непрерывности функции

1. Функция непрерывна в точке

2. Функция непрерывна в точке , если она определена в этой точке и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. вблизи точки функция принимает любое промежуточное значение между ее наименьшим значением, то есть для всех . Отсюда следует, что если в граничных точках отрезка функция имеет разные знаки, то внутри отрезка есть по крайней мере одно такое значение

Точки разрыва функции

Значения аргумента, которые не удовлетворяют условиям непрерывности, называются точками разрыва функции . При этом различают два рода точек разрыва функции.

Если при , а при и , то говорят, что функция при разрыв первого рода . Разность определяет скачок функции в точке .

Если значение функции при , то говорят, что функция непрерывна слева; если же , то говорят, что функция непрерывна справа.

Если говорят, что функция имеет в точке устранимый разрыв .

Если при , то говорят, что при разрыв второго рода .

Пример 1. Найти множество значений непрерывна.

Решение. Найдем приращение функции

При любых значениях переменной , если только

Пример 2. Доказать непрерывность функции в точке .

Решение. Для доказательства найдем приращение функции при переходе значения аргумента от к

Найдем предел приращения функции при

Так как предел приращения функции при непрерывна.

Пример 3. Определить характер разрыва функций и построить графики:

Следовательно, в точке b) При . При . Следовательно, в точке имеет разрыв первого рода и скачок функции равен .

c) Функция определена на всей числовой оси, неэлементарная, так как в точке аналитическое выражение функции меняется. Исследуем непрерывность функции в точке :

Определения точек разрыва первого и второго рода. Основные факты, используемые при исследовании функций на непрерывность. Примеры решения задач, в которых требуется найти точки разрыва и определить вид разрыва.

Определения и классификация точек разрыва функции

Определение точки разрыва функции
Конечная точка x ₀ называется точкой разрыва функции f ( x ) , если функция определена на некоторой проколотой окрестности точки x ₀ , но не является непрерывной в этой точке.

Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.

Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.

Определение точки устранимого разрыва
Точка называется точкой устранимого разрыва, если существует предел
,
но функция в точке или не определена, или не равна предельному значению: .

Таким образом, точка устранимого разрыва – это точка разрыва первого рода, в которой скачек функции равен нулю.

Определение точки разрыва 2-го рода
Точка разрыва называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.

Исследование функций на непрерывность

При исследовании функций на непрерывность мы используем следующие факты.

Примеры

Все примеры Далее мы приводим подробные решения примеров, в которых требуется исследовать функцию на непрерывность и установить вид точек разрыва, если есть.
в точках ⇓;
⇓; ⇓.

Пример 1

Все примеры ⇑ Задана функция и два значения аргумента и . Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа, установить вид разрыва; 3) сделать схематический чертеж.
.

Заданная функция является сложной. Ее можно рассматривать как композицию двух функций:
, . Тогда
.

Рассмотрим функцию . Она составлена из функции и постоянных с помощью арифметических операций сложения и деления. Функция является элементарной – степенной функцией с показателем степени 1 . Она определена и непрерывна для всех значений переменной . Поэтому функция определена и непрерывна для всех , кроме точек, в которых знаменатель дроби обращается в нуль. Приравниваем знаменатель к нулю и решаем уравнение:
.
Получаем единственный корень .
Итак, функция определена и непрерывна для всех , кроме точки .

Рассмотрим функцию . Это показательная функция с положительным основанием степени. Она определена и непрерывна для всех значений переменной .
Поэтому заданная функция определена и непрерывна для всех значений переменной , кроме точки .

Таким образом, в точке , заданная функция является непрерывной.

Рассмотрим точку . В этой точке функция не определена. Поэтому она не является непрерывной. Установим род разрыва. Для этого находим односторонние пределы.

Здесь мы использовали следующие общепринятые обозначения:
.
Также мы использовали свойство показательной функции с основанием :
.

Аналогично, для предела справа имеем:
при ,
,
,
.

Поскольку один из односторонних пределов равен бесконечности, то в точке разрыв второго рода.

В точке функция непрерывна.
В точке разрыв второго рода,
.

Пример 2

Все примеры ⇑ Задана функция . Найти точки разрыва функции, если они существуют. Указать род разрыва и скачек функции, если есть. Сделать чертеж.
.

Функция является степенной функцией с целым показателем степени, равным 1 . Такую функцию также называют линейной. Она определена и непрерывна для всех значений переменной .

В входят еще две функции: и . Они составлены из функции и постоянных с помощью арифметических операций сложения и умножения:
, .
Поэтому они также непрерывны для всех .

Поскольку функции, входящие в состав непрерывны для всех , то может иметь точки разрыва только в точках склейки ее составляющих. Это точки и . Исследуем на непрерывность в этих точках. Для этого найдем односторонние пределы.

Рассмотрим точку . Чтобы найти левый предел функции в этой точке, мы должны использовать значения этой функции в любой левой проколотой окрестности точки . Возьмем окрестность . На ней . Тогда предел слева:
.
Здесь мы использовали тот факт, что функция является непрерывной в точке (как и в любой другой точке). Поэтому ее левый (как и правый) предел равен значению функции в этой точке.

Найдем правый предел в точке . Для этого мы должны использовать значения функции в любой правой проколотой окрестности этой точки. Возьмем окрестность . На ней . Тогда предел справа:
.
Здесь мы также воспользовались непрерывностью функции .

Поскольку, в точке , предел слева не равен пределу справа, то в ней функция не является непрерывной – это точка разрыва. Поскольку односторонние пределы конечны, то это точка разрыва первого рода. Скачек функции:
.

Теперь рассмотрим точку . Тем же способом вычисляем односторонние пределы:
;
.
Поскольку функция определена в точке и левый предел равен правому, то функция непрерывна в этой точке.

Функция имеет разрыв первого рода в точке . Скачек функции в ней: . В остальных точках функция непрерывна.

Пример 3

Все примеры ⇑ Определить точки разрыва функции и исследовать характер этих точек, если
.

Воспользуемся тем, что линейная функция определена и непрерывна для всех . Заданная функция составлена из линейной функции и постоянных с помощью арифметических операций сложения, вычитания, умножения и деления:
.
Поэтому она определена и непрерывна для всех , за исключением точек, в которых знаменатель дроби обращается в нуль.

Найдем эти точки. Приравниваем знаменатель к нулю и решаем квадратное уравнение:
;
;
; .
Тогда
.

Используем формулу:
.
С ее помощью, разложим числитель на множители:
.

Тогда заданная функция примет вид:
(П1) .
Она определена и непрерывна для всех , кроме точек и . Поэтому точки и являются точками разрыва функции.

Разделим числитель и знаменатель дроби в (П1) на :
(П2) .
Такую операцию мы можем проделать, если . Таким образом,
при .
То есть функции и отличаются только в одной точке: определена при , а в этой точке не определена.

Рассмотрим точку . Знаменатель дроби в функции , при в нуль не обращается. Поэтому она определена и непрерывна при . Отсюда следует, что существует предел при и он равен значению функции в этой точке:
.
Поэтому точка является точкой устранимого разрыва первого рода.

Рассмотрим точку . Используя связь бесконечно малых и бесконечно больших функций, имеем:
;
.
Поскольку пределы бесконечные, то в этой точке разрыв второго рода.

Функция имеет точку устранимого разрыва первого рода при , и точку разрыва второго рода при .

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.

Исследование функции на непрерывность в точке проводится по уже накатанной рутинной схеме, которая состоит в проверке трёх условий непрерывности:

Исследовать функцию на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.

Решение:

1) Под прицел попадает единственная точка , в которой функция не определена.

2) Вычислим односторонние пределы:

Односторонние пределы конечны и равны.

Таким образом, в точке функция терпит устранимый разрыв.

Как выглядит график данной функции?

Хочется провести упрощение , и вроде бы получается обычная парабола. НО исходная функция не определена в точке , поэтому обязательна следующая оговорка:

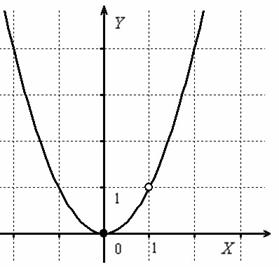
Выполним чертёж:

Ответ: функция непрерывна на всей числовой прямой кроме точки , в которой она терпит устранимый разрыв.

Функцию можно доопределить хорошим или не очень способом, но по условию этого не требуется.

Вы скажете, пример надуманный? Ничуть. Десятки раз встречалось на практике. Почти все задачи сайта родом из реальных самостоятельных и контрольных работ.

Разделаемся с любимыми модулями:

Но дроби обоих кусков предстоит сократить на . Сокращение, как и в предыдущем примере, не пройдёт без последствий. Исходная функция не определена в точке , так как знаменатель обращается в ноль. Поэтому в системе следует дополнительно указать условие , и первое неравенство сделать строгим:

Теперь об ОЧЕНЬ ПОЛЕЗНОМ приёме решения: перед чистовым оформлением задачи на черновике выгодно сделать чертёж (независимо от того, требуется он по условию или нет). Это поможет, во-первых, сразу увидеть точки непрерывности и точки разрыва, а, во-вторых, 100%-но убережёт от ошибок при нахождении односторонних пределов.

Исследуем функцию на непрерывность аналитически:

1) Функция не определена в точке , поэтому сразу можно сказать, что не является в ней непрерывной.

2) Установим характер разрыва, для этого вычислим односторонние пределы:

Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке . Заметьте, что не имеет значения, определена функция в точке разрыва или нет.

Теперь остаётся перенести чертёж с черновика (он сделан как бы с помощью исследования ;-)) и завершить задание:

Ответ: функция непрерывна на всей числовой прямой кроме точки , в которой она терпит разрыв первого рода со скачком.

Исследовать функцию на непрерывность. Определить характер разрывов функции, если они существуют. Сделать чертёж.

Это пример для самостоятельного решения, примерный образец решения в конце урока.

Перейдём к наиболее популярной и распространённой версии задания, когда функция состоит из трёх кусков:

Исследовать функцию на непрерывность и построить график функции

I) Исследуем на непрерывность точку

1) – функция определена в данной точке.

2) Найдём односторонние пределы:

Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке .

Вычислим скачок разрыва как разность правого и левого пределов:
, то есть, график рванул на одну единицу вверх.

II) Исследуем на непрерывность точку

1) – функция определена в данной точке.

2) Найдём односторонние пределы:

– односторонние пределы конечны и равны, значит, существует общий предел.

3) – предел функции в точке равен значению данной функции в данной точке.

Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.

На завершающем этапе переносим чертёж на чистовик, после чего ставим финальный аккорд:

Ответ: функция непрерывна на всей числовой прямой, кроме точки , в которой она терпит разрыв первого рода со скачком.

Исследовать функцию на непрерывность и построить её график .

Это пример для самостоятельного решения, краткое решение и примерный образец оформления задачи в конце урока.

Может сложиться впечатление, что в одной точке функция обязательно должна быть непрерывной, а в другой – обязательно должен быть разрыв. На практике это далеко не всегда так. Постарайтесь не пренебрегать оставшимися примерами – будет несколько интересных и важных фишек:

Дана функция . Исследовать функцию на непрерывность в точках . Построить график.

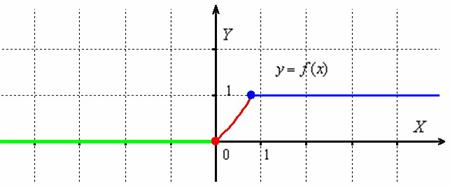
Решение: и снова сразу выполним чертёж на черновике:

Особенность данного графика состоит в том, что при кусочная функция задаётся уравнением оси абсцисс . Здесь данный участок прорисован зелёным цветом, а в тетради его обычно жирно выделяют простым карандашом. И, конечно же, не забываем про наших баранов: значение относится к ветке тангенса (красная точка), а значение принадлежит прямой .

Из чертежа всё понятно – функция непрерывна на всей числовой прямой, осталось оформить решение, которое доводится до полного автоматизма буквально после 3-4-х подобных примеров:

I) Исследуем на непрерывность точку

1) – функция определена в данной точке.

2) Вычислим односторонние пределы:

, значит, общий предел существует.

3) – предел функции в точке равен значению данной функции в данной точке.

Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.

II) Исследуем на непрерывность точку

1) – функция определена в данной точке.

2) Найдём односторонние пределы:

И здесь, в правостороннем пределе – предел единицы равен самой единице.

– общий предел существует.

3) – предел функции в точке равен значению данной функции в данной точке.

Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.

Как обычно, после исследования переносим наш чертёж на чистовик.

Ответ: функция непрерывна в точках .

Обратите внимание, что в условии нас ничего не спрашивали про исследование всей функции на непрерывность, и хорошим математическим тоном считается формулировать точный и чёткий ответ на поставленный вопрос. Кстати, если по условию не требуется строить график, то вы имеете полное право его и не строить (правда, потом преподаватель может заставить это сделать).

Исследовать функцию на непрерывность в точках . Классифицировать точки разрыва, если они есть. Выполнить чертёж.

Как вы помните, я рекомендовал незамедлительно выполнять чертёж на черновике, но время от времени попадаются такие примеры, где не сразу сообразишь, как выглядит график. Поэтому в ряде случаев выгодно сначала найти односторонние пределы и только потом на основе исследования изобразить ветви. В двух заключительных примерах мы, кроме того, освоим технику вычисления некоторых односторонних пределов:

Исследовать на непрерывность функцию и построить её схематический график.

Решение: нехорошие точки очевидны: (обращает в ноль знаменатель показателя) и (обращает в ноль знаменатель всей дроби). Малопонятно, как выглядит график данной функции, а значит, сначала лучше провести исследование:

I) Исследуем на непрерывность точку

1) Функция не определена в данной точке.

2) Найдём односторонние пределы:

Вычислим правосторонний предел:

Правосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке .

II) Исследуем на непрерывность точку

1) Функция не определена в данной точке.

2) Вычислим левосторонний предел:

Правосторонний предел, как брат близнец, за тем лишь исключением, что в знаменателе выплывает бесконечно малое отрицательное число:

Односторонние пределы бесконечны, значит, функция терпит разрыв 2-го рода в точке .

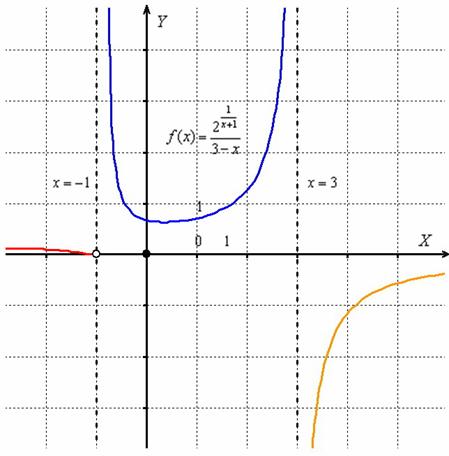
Прямые являются вертикальными асимптотами для графика данной функции.

Ответ: функция непрерывна на всей числовой прямой кроме точек , в которых она терпит разрывы 2-го рода.

Более простая функция для самостоятельного решения:

Исследовать на непрерывность функцию и выполнить схематический чертёж.

Примерный образец решения в конце, который подкрался незаметно.

До скорых встреч!

Решения и ответы:

Пример 3: Решение: преобразуем функцию: . Учитывая правило раскрытия модуля и тот факт, что , перепишем функцию в кусочном виде:

Исследуем функцию на непрерывность.

1) Функция не определена в точке .

2) Вычислим односторонние пределы:

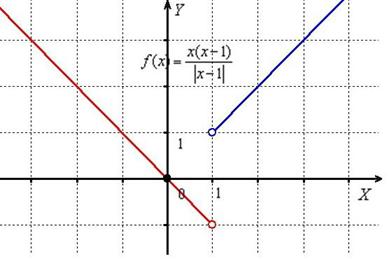
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке . Выполним чертёж:

Ответ: функция непрерывна на всей числовой прямой кроме точки , в которой она терпит разрыв первого рода со скачком. Скачок разрыва: (две единицы вверх).

Пример 5: Решение: каждая из трёх частей функции непрерывна на своём интервале.
I) Исследуем на непрерывность точку
1) – функция определена в данной точке.

2) Вычислим односторонние пределы:

, значит, общий предел существует.
3) – предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.
II) Исследуем на непрерывность точку

1) – функция определена в данной точке.

2) Найдём односторонние пределы:

Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке .
Скачок разрыва: (пять единиц вниз).
Чертёж можно найти в первой части статьи.
Ответ: функция непрерывна на всей числовой прямой, кроме точки , в которой она терпит разрыв первого рода со скачком.

I) Исследуем на непрерывность точку

1) – функция определена в данной точке.

2) Найдём односторонние пределы:

Левосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке .
II) Исследуем на непрерывность точку

1) – функция определена в данной точке.

2) Найдём односторонние пределы:

Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке .
Выполним чертёж:

Ответ: В точке функция терпит разрыв 2-го рода, в точке функция терпит разрыв 1-го рода со скачком.

Пример 9: Решение: исследуем на непрерывность точку :

1) Функция не определена в данной точке.

2) Вычислим односторонние пределы:

Левосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке .
Выполним чертёж:

Ответ: функция непрерывна на всей числовой прямой кроме точки , в которой она терпит разрыв 2-го рода.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Как найти область определения функции?

Если где-то нет чего-то, значит, где-то что-то есть

Предполагается, читатель знает области определения основных функций: линейной, квадратичной, кубической функции, многочленов, экспоненты, логарифма, синуса, косинуса. Они определены на . За тангенсы, арксинусы, так и быть, прощаю =) Более редкие графики запоминаются далеко не сразу.

Да, кстати, если что-нибудь не понятно из терминологии и/или содержания первых абзацев, таки лучше вернуться к статье Графики и свойства элементарных функций.

Приращением аргумента называют разность $$ \triangle x= x-x_0 $$ где x - произвольное число, которое мало отличается от начальной точки $x_0$. Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ \triangle y=f(x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.

п.2. Непрерывность функции в точке и на промежутке

Функция $y=f(x)$ непрерывна в точке $x_0$, если в этой точке малому приращению аргумента $\triangle x=x-x_0$ соответствует малое приращение функции $\triangle y=f(x)-f(x_0)$: $$ \lim_\triangle y=\lim_\triangle y=0 $$

ε-δ определение непрерывности похоже на ε-δ определение предела функции, с той разницей, что модуль $|x-x_0|$ может быть равен 0 для непрерывной функции, т.е. сама точка $x_0$ входит в δ-окрестность.

Проанализируем предел приращения функции: \begin \lim_\triangle y= \lim_\left(f(x)-f(x_0)\right)= \lim_f(x)-\lim_f(x_0)=\\ =\lim_f(x)-f(x_0) \end т.к. $f(x_0)$ - величина постоянная и от $\triangle x$ не зависит.
Для непрерывной функции: $$ \lim_\triangle y =0 \Leftrightarrow \lim_f(x)-f(x_0)=0\Leftrightarrow \lim_f(x)=f(x_0) $$ Учитывая, что $\triangle x\rightarrow 0\Leftrightarrow x-x_0\rightarrow 0\Leftrightarrow x\rightarrow x_0$
получаем $\limf(x)=f(x_0).$

Функция $y=f(x)$ непрерывна в точке $x_0$, если существует предел функции в этой точке и он равен значению функции в точке: $$ \limf(x)=f(x_0) $$

Все три представленных определения непрерывности функции в точке эквивалентны.
Существуют и другие эквивалентные определения. Мы дадим ещё одно из них дальше, в этом же параграфе.

п.3. Непрерывность функции на промежутке

Промежуток – это интервал, отрезок, луч и т.п. (см. §16 справочника для 8 класса).

Непрерывная функция

Кусочно-непрерывная функция

п.4. Односторонние пределы

Односторонний предел – это предел числовой функции при приближении к предельной точке с определенной стороны (слева или справа).
Обозначение односторонних пределов: \begin \lim_f(x)=a -\ \text\\ \lim_f(x)=b -\ \text \end

Рассмотрим гиперболу $y=\frac$.

У этой гиперболы две асимптоты $y=0$ и $x=2$.
Точка $x_0=2$ не входит в область определения.
Если мы будем приближаться к $x_0=2$ слева , начав, например с 1,5, мы будем постепенно опускаться по ветке гиперболы на минус бесконечность. Т.е., левый предел: $$ \lim_\frac=-\infty $$

Если же мы будем приближаться к $x_0=2$ справа , начав, например с 2,5, мы будем постепенно подниматься по ветке гиперболы на плюс бесконечность. Т.е., правый предел: $$ \lim_\frac=+\infty $$ Левый и правый пределы в точке $x_0=2$ для данной гиперболы не равны: $$ \lim_\frac \ne \lim_\frac $$

Теперь рассмотрим параболу $y=x^2-2$
Областью определения параболы является вся числовая прямая $x\in\mathbb$

В этом случае, если приближаться к $x_0=2$ слева , мы получаем: $$ \lim_(x^2-2)=2 $$ И если приближаться $x_0=2$ справа , мы тоже получаем: $$ \lim_(x^2-2)=2 $$ Левый и правый пределы равны: $$ \lim_(x^2-2) =\lim_(x^2-2) $$

Функция $y=f(x)$ непрерывна в точке $x_0$, если одновременно выполняются следующие три условия:
1) точка $x_0$ принадлежит области определения функции $x\in D$;
2) левый и правый пределы в точке $x_0$ равны и конечны: $$ \lim_f(x) =\lim_f(x)=\lim_f(x)=a\ne\infty $$ 3) предел функции в точке $x_0$ равен значению функции в этой точке: $$ \lim_f(x)=f(x_0) $$

Это еще одно определение непрерывности, которым удобно пользоваться на практике.

п.5. Классификация точек разрыва

Точка $x_0$ будет точкой разрыва для функции $y=f(x)$, если выполняется хотя бы одно из условий:
1) точка $x_0$ не принадлежит области определения функции $x\notin D$;
2) левый и правый пределы в точке $x_0$ не равны или бесконечны: $$ \lim_f(x) \ne\lim_f(x)\ \text\ \lim_f(x) =\lim_f(x)=\pm\infty $$ 3) предел функции в точке $x_0$ не совпадает со значением функции в этой точке: $$ \lim_f(x)\ne f(x_0) $$

Точки разрыва	1-го рода Односторонние пределы существуют и конечны	Устранимые Односторонние пределы равны между собой, но не равны $f(x_0)$
		Неустранимые (скачок) Односторонние пределы не равны между собой
	2-го рода Хотя бы один из односторонних пределов бесконечен или не существует

п.6. Точки разрыва первого рода

Устранимые точки разрыва 1-го рода
Левый и правый пределы в точке $x_0$ равны и конечны: $$ \lim_f(x)=\lim_f(x)=\lim_f(x)=a\ne\infty $$ НО:
либо точка $x_0$ НЕ принадлежит области определения функции $x\notin D$;
либо предел НЕ равен значению функции в точке $x_0$: $\lim_f(x)\ne f(x_0)$

$y=\frac, x_0=2$
Эта функция эквивалентна системе $$ y=\frac \Leftrightarrow \begin y=x+2\\ x\ne 2 \end $$ При этом $\lim_(x+2)=\lim_(x+2)=4$
В точке $x_0=2\notin D$ функция имеет устранимый разрыв.

Неустранимые точки разрыва 2-го рода (скачок)
Левый и правый пределы в точке $x_0$ конечны, но не равны: $$ \begin \lim_f(x)=a\ne\infty\\ \lim_f(x)=b\ne\infty\\ a\ne b \end $$ Такой разрыв также называют скачком .
Величина скачка рассчитывается по формуле: $$ \triangle y=\lim_f(x)- \lim_f(x)=b-a $$

п.7. Точки разрыва второго рода

В точках разрыва 2-го рода хотя бы один из односторонних пределов бесконечен или не существует.

$x_0=0\ne D$ - точка не входит в ОДЗ
Односторонние пределы: \begin \lim_e^\frac1x=e^>=e^<-\infty>=0\\ \lim_e^\frac1x=e^>=e^<+\infty>=+\infty \end Пределы не равны между собой, и один и них бесконечен.

п.8. Алгоритм исследования функции на непрерывность

На входе: функция $y=f(x)$
Шаг 1. Найти ОДЗ функции, определить точки и промежутки, не принадлежащие ОДЗ.
Шаг 2. Составить множество точек, в которое входят точки и границы промежутков, не принадлежащие ОДЗ, а также – для кусочно-непрерывных функций – точки сшивания. Полученное множество состоит из точек, подозрительных на разрыв.
Шаг 3. Исследовать каждую из точек, подозрительных на разрыв, с помощью односторонних пределов. Если разрыв обнаружен, определить тип разрыва.
На выходе: список точек разрыва и тип разрыва для каждой точки.

п.9. Примеры

Пример 1. Исследуйте функцию на непрерывность:
a) $ y=\frac $
ОДЗ: $x-1\ne 0\Rightarrow x\ne 1$
$x_0=1\notin D$ - точка не входит в ОДЗ, подозрительная на разрыв.
Найдем односторонние пределы: \begin \lim_\frac=\frac=\frac=-\infty\\ \lim_\frac=\frac=\frac=+\infty \end Односторонние пределы не равны и бесконечны.
Точка $x_0=1$ - точка разрыва 2-го рода.

б) $ y=\frac-2> $
ОДЗ: $ \begin x+2\geq 0\\ \sqrt-2\ne 0 \end \Rightarrow \begin x\geq -2\\ \sqrt\ne 2 \end \Rightarrow \begin x\geq -2\\ x\ne 2 \end $
$x_0=-2$ - левая граница ОДЗ
$x_1=2\notin D$- точка не входит в ОДЗ
Точки $x_0$ и $x_1$ - подозрительные на разрыв

Исследуем $x_0=-2$. Найдем односторонние пределы: \begin \lim_\frac-2> - \text\\ \lim_\frac-2>=\frac-2>=\frac=1 \end Один из односторонних пределов не существует.
Точка $x_0=-2$ - точка разрыва 2-го рода.

Исследуем $x_1=2$. Найдем односторонние пределы: \begin \lim_\frac-2> =\frac-2>=\frac=-\infty\\ \lim_\frac-2>=\frac-2>=\frac=+\infty \end Односторонние пределы не равны и бесконечны.
Точка $x_1=2$ - точка разрыва 2-го рода.

в) $ y=\frac $
ОДЗ: $x\ne 0$
$x_0=0\notin D$- точка не входит в ОДЗ, подозрительная на разрыв
Найдем односторонние пределы: \begin \lim_\frac=\frac13\lim_\frac=\frac13\cdot 1=\frac13\\ \lim_\frac=\frac13\lim_\frac=\frac13\cdot 1=\frac13 \end Односторонние пределы конечны и равны.
Точка $x_0=0$ - точка разрыва 1-го рода, устранимый разрыв.

г) $ y= \begin x+1,\ x\lt 3\\ x^2+3,\ x\geq 3 \end $
ОДЗ: $x\in\mathbb$
$x_0=3$- точка сшивания, подозрительная на разрыв.
Найдем односторонние пределы: \begin \lim_y=\lim_(x+1)=3+1=4\\ \lim_y=\lim_(x^2+3)=3^2+3=12 \end Односторонние пределы конечны, но неравны.
Точка $x_0=3$ - точка разрыва 1-го рода, неустранимый разрыв (скачок).
Величина скачка: $\lim_y-\lim_y=12-4=8$

Пример 2. Доопределите функцию в точке разрыва так, чтобы она стала непрерывной в этой точке:
a) $ y=\frac $
ОДЗ: $x\ne 0$
$x_0=0\notin D$- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: $\frac=\frac=\frac$ $$ y=\frac\Leftrightarrow y= \begin \frac\\ x\ne 0 \end $$ Найдем односторонние пределы: \begin \lim_\frac=0,\ \ \lim_\frac=0 \end Односторонние пределы конечны и равны.
Точка $x_0=0$ - точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: $y(0)=0$.
Доопределенная непрерывная функция: $$ y= \begin \frac,\ x\ne 0\\ 0,\ \ x=0 \end $$ б) $ y=\frac $
ОДЗ: $x\ne 0$
$x_0=0\notin D$- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: $\frac=\frac=\frac>=8\left(\frac\right)^2$ $$ y=\frac\Leftrightarrow y= \begin 8\left(\frac\right)^2\\ x\ne 0 \end $$ Найдем односторонние пределы: \begin \lim_8\left(\frac\right)^2=8\cdot 1=8,\ \ \lim_8\left(\frac\right)^2=8\cdot 1=8 \end Односторонние пределы конечны и равны.
Точка $x_0=0$ - точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: $y(0)=8$.
Доопределенная непрерывная функция: $$ y= \begin \frac,\ x\ne 0\\ 8,\ \ x=0 \end $$

Пример №1 . Доказать, что функция y=sinx непрерывна при любом значении x .
Решение. Пусть x₀ – произвольная точка. Придавая ей приращение Δx, получим точку x=x₀+Δx. Тогда Δy=f(x)-f(x₀) = sin(x₀+Δx)-sin(x) = . Получаем .

Определение. Функция y=f(x) называется непрерывной в точке x₀ справа (слева), если

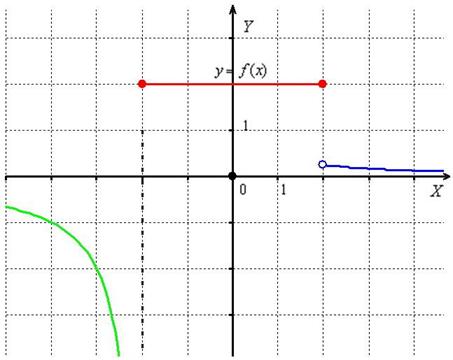
Функция, непрерывная во внутренней точке, будет одновременно непрерывной справа и слева. Справедливо и обратное утверждение: если функция непрерывна в точке слева и справа, то она будет непрерывной в этой точке. Однако функция может быть непрерывной только с одной стороны. Например, для , , f(1)=1, следовательно, эта функция непрерывна только слева (график этой функции см. выше в пункте 5.7.2).
Определение. Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.
В частности, если промежутком является отрезок [a,b], то на его концах подразумевается односторонняя непрерывность.

Свойства непрерывных функций

1. Все элементарные функции непрерывны в своей области определения.
2. Если f(x) и φ(x), заданные на некотором промежутке, непрерывны в точке x₀ этого промежутка, то в этой точке будут также непрерывны функции

3. Если y=f(x) непрерывна в точке x₀ из X, а z=φ(y) непрерывна в соответствующей точке y₀=f(x₀) из Y, то и сложная функция z=φ(f(x)) будет непрерывной в точке x₀.

Разрывы функции и их классификация

Признаком непрерывности функции f(x) в точке x₀ служит равенство , которое подразумевает наличие трех условий:
1) f(x) определена в точке x₀;
2) ;
3) .
Если хотя бы одно из этих требований нарушено, то x₀ называют точкой разрыва функции. Другими словами, точкой разрыва называется точка, в которой эта функция не является непрерывной. Из определения точек разрыва следует, что точками разрыва функции являются:
а) точки, принадлежащие области определения функции, в которых f(x) теряет свойство непрерывности,
б) точки, не принадлежащие области определения f(x), которые являются смежными точками двух промежутков области определения функции.
Например, для функции точка x=0 есть точка разрыва, так как функция в этой точке не определена, а функция имеет разрыв в точке x=1, являющейся смежной для двух промежутков (-∞,1) и (1,∞) области определения f(x) и не существует.

Для точек разрыва принята следующая классификация.
1) Если в точке x₀ имеются конечные и , но f(x₀+0)≠f(x₀-0), то x₀ называется точкой разрыва первого рода, при этом называют скачком функции.

Пример 2. Рассмотрим функцию
Разрыв функции возможен только в точке x=2 (в остальных точках она непрерывна как всякий многочлен).
Найдем , . Так как односторонние пределы конечны, но не равны друг другу, то в точке x=2 функция имеет разрыв первого рода. Заметим, что , следовательно функция в этой точке непрерывна справа (рис. 2).
2) Точками разрыва второго рода называются точки, в которых хотя бы один из односторонних пределов равен ∞ или не существует.

, и функция станет непрерывной в точке x₀.
Пример 4. Известно, что , причем этот предел не зависит от способа стремления x к нулю. Но функция в точке x=0 не определена. Если доопределим функцию, положив f(0)=1, то она окажется непрерывной в этой точке (в остальных точках она непрерывна как частное непрерывных функций sinx и x).
Пример 5. Исследовать на непрерывность функцию .
Решение. Функции y=x 3 и y=2x определены и непрерывны всюду, в том числе и в указанных промежутках. Исследуем точку стыка промежутков x=0:
, , f(0)=0 . Получаем, что , откуда следует, что в точке x=0 функция непрерывна.
Определение. Функция, непрерывная на промежутке за исключением конечного числа точек разрыва первого рода или устранимого разрыва, называется кусочно-непрерывной на этом промежутке.

Примеры разрывных функций

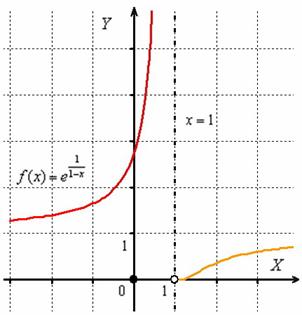
Пример 1. Функция определена и непрерывна на (-∞,+∞) за исключением точки x=2. Определим тип разрыва. Поскольку и , то в точке x=2 разрыв второго рода (рис. 6).
Пример 2. Функция определена и непрерывна при всех x, кроме x=0, где знаменатель равен нулю. Найдем односторонние пределы в точке x=0:

Односторонние пределы конечны и различны, следовательно, x=0 – точка разрыва первого рода (рис. 7).
Пример 3. Установить, в каких точках и какого рода разрывы имеет функция
Эта функция определена на [-2,2]. Так как x 2 и 1/x непрерывны соответственно в промежутках [-2,0] и [0,2], то разрыв может быть только на стыке промежутков, то есть в точке x=0. Поскольку

Пример 4. Можно ли устранить разрывы функций:
а) в точке x=2;
б) в точке x=2;
в) в точке x=1?
Решение. О примере а) сразу можно сказать, что разрыв f(x) в точке x=2 устранить невозможно, так как в этой точке бесконечные односторонние пределы (см. пример 1).
б) Функция g(x) хотя имеет конечные односторонние пределы в точке x=2
(,),
но они не совпадают, поэтому разрыв также устранить нельзя.
в) Функция φ(x) в точке разрыва x=1 имеет равные односторонние конечные пределы: . Следовательно, разрыв может быть устранен переопределением функции в точке x=1, если положить f(1)=1 вместо f(1)=2.

Пример №5 . Показать, что функция Дирихле

разрывна в каждой точке числовой оси.
Решение. Пусть x₀ – любая точка из (-∞,+∞). В любой ее окрестности найдутся как рациональные, так и иррациональные точки. Значит, в любой окрестности x₀ функция будет иметь значения, равные 0 и 1. В таком случае не может существовать предела функции в точке x₀ ни слева, ни справа, значит функция Дирихле в каждой точке числовой оси имеет разрывы второго рода.

Пример 6 . Найти точки разрыва функции

и определить их тип.
Решение. Точками, подозрительными на разрыв, являются точки x₁=2, x₂=5, x₃=3.
В точке x₁=2 f(x) имеет разрыв второго рода, так как

Точка x₂=5 является точкой непрерывности, так как значение функции в этой точке и в ее окрестности определяется второй строкой, а не первой: .
Исследуем точку x₃=3: , , откуда следует, что x=3 – точка разрыва первого рода.

Для самостоятельного решения.
Исследовать функции на непрерывность и определить тип точек разрыва:
1) ; Ответ: x=-1 – точка устранимого разрыва;
2) ; Ответ: Разрыв второго рода в точке x=8;
3) ; Ответ: Разрыв первого рода при x=1;
4)
Ответ: В точке x₁=-5 устранимый разрыв, в x₂=1 – разрыв второго рода и в точке x₃=0 - разрыв первого рода.
5) Как следует выбрать число A, чтобы функция

была бы непрерывной в точке x=0?
Ответ: A=2.
6) Можно ли подобрать число A так, чтобы функция

была бы непрерывной в точке x=2?
Ответ: нет.

Задана функция y=f(x) и два значения аргумента x₁ и x₂. Требуется: 1) установить, является ли данная функция непрерывной или разрывной из данных значений аргумента; 2) в случае разрыва определить, какого он рода; 3) все рассуждения обосновать.
, x₁ = 1, x₂ = 3
Решение:
а)
Предел конечен и равен числу. Следовательно, в точке x₁ функция непрерывна.

Предел в точке x = 3 не существует. Следовательно, в этой точке функция имеет разрыв. Поскольку один из пределов равен бесконечности, то эта точка разрыва второго рода.

Читайте также: