Как сделать четную и нечетную функцию
Обновлено: 30.06.2024
График четной функции симметричен относительно оси ординат.
Например, — четные функции.

Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство
График нечетной функции симметричен относительно начала координат.
Например, — нечетные функции.

Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.
Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:
1. Проверьте, является ли функция четной (нечетной).
Область определения функции
Проверим, является ли чётной или нечётной. Если функция четна. Если функция нечетна.
График четной функции симметричен относительно оси \(y\) :

Пример: функция \(f(x)=x^2+\cos x\) является четной, т.к. \(f(-x)=(-x)^2+\cos=x^2+\cos x=f(x)\) .
\(\blacktriangleright\) Функция \(f(x)\) называется нечетной, если при всех \(x\) из ее области определения верно: \(f(-x)=-f(x)\) .
График нечетной функции симметричен относительно начала координат:

Пример: функция \(f(x)=x^3+x\) является нечетной, т.к. \(f(-x)=(-x)^3+(-x)=-x^3-x=-(x^3+x)=-f(x)\) .
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
Например, функция \(f(x)=x^2-x\) является суммой четной функции \(f_1=x^2\) и нечетной \(f_2=-x\) .
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
5) Если \(f(x)\) — четная функция, то уравнение \(f(x)=c \ (c\in \mathbb\) ) имеет единственный корень тогда и только когда, когда \(x=0\) .
6) Если \(f(x)\) — четная или нечетная функция, и уравнение \(f(x)=0\) имеет корень \(x=b\) , то это уравнение обязательно будет иметь второй корень \(x=-b\) .
\(\blacktriangleright\) Функция \(f(x)\) называется периодической на \(X\) , если для некоторого числа \(T\ne 0\) выполнено \(f(x)=f(x+T)\) , где \(x, x+T\in X\) . Наименьшее \(T\) , для которого выполнено данное равенство, называется главным (основным) периодом функции.
У периодической функции любое число вида \(nT\) , где \(n\in \mathbb\) также будет являться периодом.
Пример: любая тригонометрическая функция является периодической;
у функций \(f(x)=\sin x\) и \(f(x)=\cos x\) главный период равен \(2\pi\) , у функций \(f(x)=\mathrm\,x\) и \(f(x)=\mathrm\,x\) главный период равен \(\pi\) .

Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:

\(\blacktriangleright\) Область определения \(D(f)\) функции \(f(x)\) — это множество, состоящее из всех значений аргумента \(x\) , при которых функция имеет смысл (определена).
Пример: у функции \(f(x)=\sqrt x+1\) область определения: \(x\in [0;+\infty)\) .
\(\blacktriangleright\) Область значений \(E(f)\) функции \(f(x)\) — это множество, состоящее из всех значений функции \(f(a)\) , где \(a\in D(f)\) .
Пример: у функции \(f(x)=\sqrt x +1\) область значений: \(f(x)\in [1;+\infty)\) .
\(\blacktriangleright\) Уравнение \(f(x)=a\) имеет решение тогда и только тогда, когда \(a\) принадлежит области значений функции \(f(x)\) , т.е. \(a\in E(f)\) .
\(\blacktriangleright\) Если область значений функции \(f(x)\) не превышает некоторого числа \(A\) , т.е. \(f(x)\leq A\) при всех \(x\in D(f)\) , а функция \(g(x)\geq A\) при всех \(x\in D(g)\) , то уравнение \[<\large
При каких значениях параметра \(a\) уравнение
имеет единственное решение?
Заметим, что так как \(x^2\) и \(\cos x\) — четные функции, то если уравнение будет иметь корень \(x_0\) , оно также будет иметь и корень \(-x_0\) .
Действительно, пусть \(x_0\) – корень, то есть равенство \(2x_0^2+a\mathrm\,(\cos x_0)+a^2=0\) верно. Подставим \(-x_0\) : \(2 (-x_0)^2+a\mathrm\,(\cos(-x_0))+a^2=2x_0^2+a\mathrm\,(\cos x_0)+a^2=0\) .
Таким образом, если \(x_0\ne 0\) , то уравнение уже будет иметь как минимум два корня. Следовательно, \(x_0=0\) . Тогда:
\[2\cdot 0+a\mathrm\,(\cos 0)+a^2=0 \quad \Rightarrow \quad a^2+a\mathrm\,1=0 \quad \Rightarrow \quad \left[ \begin\begin &a=0\\ &a=-\mathrm\,1 \end \end\right.\]
Мы получили два значения параметра \(a\) . Заметим, что мы использовали то, что \(x=0\) точно является корнем исходного уравнения. Но мы нигде не использовали то, что он единственный. Следовательно, нужно подставить получившиеся значения параметра \(a\) в исходное уравнение и проверить, при каких именно \(a\) корень \(x=0\) действительно будет единственным.
1) Если \(a=0\) , то уравнение примет вид \(2x^2=0\) . Очевидно, что это уравнение имеет лишь один корень \(x=0\) . Следовательно, значение \(a=0\) нам подходит.
2) Если \(a=-\mathrm\,1\) , то уравнение примет вид \[2x^2-\mathrm\,1\cdot \mathrm\,(\cos x)+\mathrm^2\,1=0\] Перепишем уравнение в виде \[2x^2+\mathrm^2\,1=\mathrm\,1\cdot \mathrm\,(\cos x)\qquad (*)\] Так как \(-1\leqslant \cos x\leqslant 1\) , то \(-\mathrm\,1\leqslant \mathrm\,(\cos x)\leqslant \mathrm\,1\) . Следовательно, значения правой части уравнения (*) принадлежат отрезку \([-\mathrm^2\,1; \mathrm^2\,1]\) .
Так как \(x^2\geqslant 0\) , то левая часть уравнения (*) больше или равна \(0+ \mathrm^2\,1\) .
Таким образом, равенство (*) может выполняться только тогда, когда обе части уравнения равны \(\mathrm^2\,1\) . А это значит, что \[\begin 2x^2+\mathrm^2\,1=\mathrm^2\,1 \\ \mathrm\,1\cdot \mathrm\,(\cos x)=\mathrm^2\,1 \end \quad\Leftrightarrow\quad \begin x=0\\ \mathrm\,(\cos x)=\mathrm\,1 \end\quad\Leftrightarrow\quad x=0\] Следовательно, значение \(a=-\mathrm\,1\) нам подходит.
Найдите все значения параметра \(a\) , при каждом из которых график функции \[f(x)=3\mathrm\,\dfrac5 +2\sin \dfrac<8\pi a-3x>4\]
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\[\begin &3\mathrm\,\left(-\dfrac5\right)+2\sin \dfrac<8\pi a+3x>4= -\left(3\mathrm\,\left(\dfrac5\right)+2\sin \dfrac<8\pi a-3x>4\right)\quad \Rightarrow\quad -3\mathrm\,\dfrac5+2\sin \dfrac<8\pi a+3x>4= -\left(3\mathrm\,\left(\dfrac5\right)+2\sin \dfrac<8\pi a-3x>4\right) \quad \Rightarrow\\[3ex] \Rightarrow\quad &\sin \dfrac<8\pi a+3x>4+\sin \dfrac<8\pi a-3x>4=0 \quad \Rightarrow \quad2\sin \dfrac12\left(\dfrac<8\pi a+3x>4+\dfrac<8\pi a-3x>4\right)\cdot \cos \dfrac12 \left(\dfrac<8\pi a+3x>4-\dfrac<8\pi a-3x>4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \frac34 x=0 \end\]
Последнее уравнение должно быть выполнено для всех \(x\) из области определения \(f(x)\) , следовательно, \(\sin(2\pi a)=0 \Rightarrow a=\dfrac n2, n\in\mathbb\) .
\(\dfrac n2, n\in\mathbb\)
Найдите все значения параметра \(a\) , при каждом из которых уравнение \[f(x)=|a+2|\sqrt[3]x\] имеет 4 решения, где \(f\) – четная периодическая с периодом \(T=\dfrac3\) функция, определенная на всей числовой прямой, причем \(f(x)=ax^2\) при \(0\leqslant x\leqslant \dfrac83.\)
(Задача от подписчиков)
Так как \(f(x)\) – четная функция, то ее график симметричен относительно оси ординат, следовательно, при \(-\dfrac83\leqslant x\leqslant 0\) \(f(x)=ax^2\) . Таким образом, при \(-\dfrac83\leqslant x\leqslant \dfrac83\) , а это отрезок длиной \(\dfrac3\) , функция \(f(x)=ax^2\) .
1) Пусть \(a>0\) . Тогда график функции \(f(x)\) будет выглядеть следующим образом:
Тогда для того, чтобы уравнение имело 4 решения, нужно, чтобы график \(g(x)=|a+2|\cdot \sqrt[3]x\) проходил через точку \(A\) :
Следовательно, \[\dfrac9a=|a+2|\cdot \sqrt[3]8 \quad\Leftrightarrow\quad \left[\begin\begin &9(a+2)=32a\\ &9(a+2)=-32a \end \end\right. \quad\Leftrightarrow\quad \left[\begin\begin &a=\dfrac\\[2ex] &a=-\dfrac \end \end\right.\] Так как \(a>0\) , то подходит \(a=\dfrac\) .

2) Пусть \(a . Тогда картинка окажется симметричной относительно начала координат:
Нужно, чтобы график \(g(x)\) прошел через точку \(B\) : \[\dfrac9a=|a+2|\cdot \sqrt[3] \quad\Leftrightarrow\quad \left[\begin\begin &a=\dfrac\\[2ex] &a=-\dfrac \end \end\right.\] Так как \(a , то подходит \(a=-\dfrac\) .
3) Случай, когда \(a=0\) , не подходит, так как тогда \(f(x)=0\) при всех \(x\) , \(g(x)=2\sqrt[3]x\) и уравнение будет иметь только 1 корень.
имеет хотя бы один корень.
(Задача от подписчиков)
Найдите все значения параметра \(a\) , при каждом из которых уравнение \[2^+(a-10)\cdot (\sqrt2)^+12-a=0\]
имеет шесть различных решений.
Сделаем замену \((\sqrt2)^=t\) , \(t>0\) . Тогда уравнение примет вид \[t^2+(a-10)t+12-a=0\quad (*)\] Будем постепенно выписывать условия, при которых исходное уравнение будет иметь шесть решений.
Заметим, что квадратное уравнение \((*)\) может максимум иметь два решения. Любое кубическое уравнение \(Ax^3+Bx^2+Cx+D=0\) может иметь не более трех решений. Следовательно, если уравнение \((*)\) имеет два различных решения (положительных!, так как \(t\) должно быть больше нуля) \(t_1\) и \(t_2\) , то, сделав обратную замену, мы получим: \[\left[\begin\begin &(\sqrt2)^=t_1\\[2ex] &(\sqrt2)^=t_2\end\end\right.\] Так как любое положительное число можно представить как \(\sqrt2\) в какой-то степени, например, \(t_1=(\sqrt2)^ <\log_t_1>\) , то первое уравнение совокупности перепишется в виде \[x^3-3x^2+4=\log_ t_1\] Как мы уже говорили, любое кубическое уравнение имеет не более трех решений, следовательно, каждое уравнение из совокупности будет иметь не более трех решений. А значит и вся совокупность будет иметь не более шести решений.
Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение \((*)\) должно иметь два различных решения, а каждое полученное кубическое уравнение (из совокупности) должно иметь три различных решения (причем ни одно решение одного уравнения не должно совпадать с каким-либо решением второго!)
Очевидно, что если квадратное уравнение \((*)\) будет иметь одно решение, то мы никак не получим шесть решений у исходного уравнения.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin 12-a>0\\-(a-10)>0\end\quad\Leftrightarrow\quad a
Таким образом, мы уже обеспечили себе два различных положительных корня \(t_1\) и \(t_2\) .

3) Давайте посмотрим на такое уравнение \[x^3-3x^2+4=\log_ t\] При каких \(t\) оно будет иметь три различных решения?
Рассмотрим функцию \(f(x)=x^3-3x^2+4\) .
Можно разложить на множители: \[x^3-3x^2+4=x^3+x^2-4x^2+4=x^2(x+1)-4(x+1)(x-1)=(x+1)(x-2)^2\] Следовательно, ее нули: \(x=-1;2\) .
Если найти производную \(f'(x)=3x^2-6x\) , то мы получим две точки экстремума \(x_=0, x_=2\) .
Следовательно, график выглядит так:
Мы видим, что любая горизонтальная прямая \(y=k\) , где \(0 , пересекает график в трех точках. При всех остальных значениях \(k\) будет меньше трех точек пересечения. Следовательно, для того, чтобы уравнение \(x^3-3x^2+4=\log_ t\) имело три различных решения, нужно, чтобы \(0 .
Таким образом, нужно: \[\begin 0 Давайте также сразу заметим, что если числа \(t_1\) и \(t_2\) различны, то и числа \(\log_t_1\) и \(\log_t_2\) будут различны, значит, и уравнения \(x^3-3x^2+4=\log_ t_1\) и \(x^3-3x^2+4=\log_ t_2\) будут иметь несовпадающие между собой корни.
Систему \((**)\) можно переписать так: \[\begin 1
Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.
Четная функция
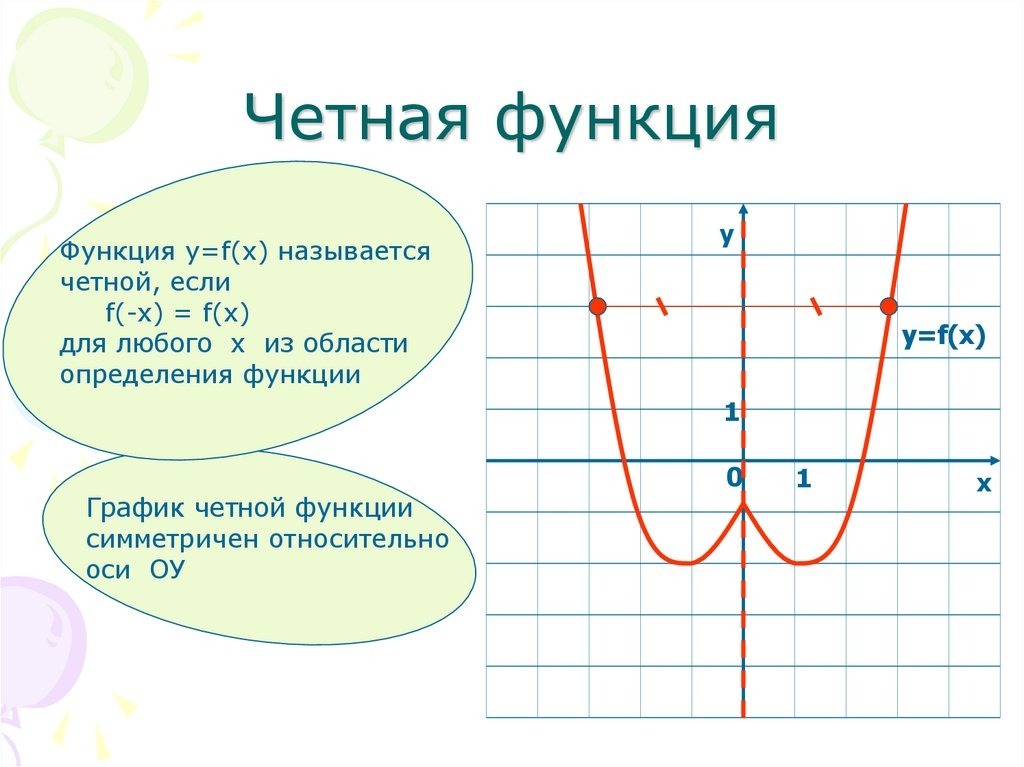
Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
График четной функции симметричен относительно оси Ох.
Возьмем произвольную точку \(M(x,\;f(x))\) из области определения \(f(x)\) , тогда точка \(M_1(-x,\;f(x))\) так же будет принадлежать графику, что следует из определения. Значит график данной функции будет симметричен относительно оси ординат.
Нечетная функция
Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)
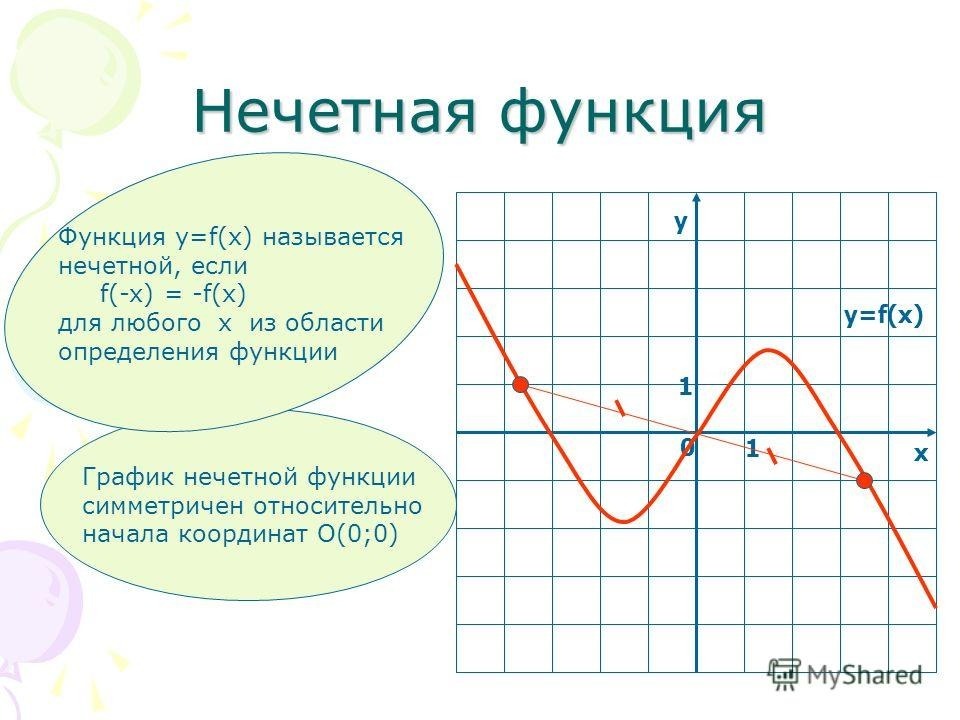
График нечетной функции симметричен относительно начала координат (точки (0;0)).
Возьмем произвольную точку \(M(x,\;f(x))\) из области определения \(f(x)\) , тогда точка \(M_1(-x,\;-f(x))\) также будет принадлежать графику, что следует из определения. Значит график данной функции будет симметричен относительно начала координат.
Произведение четной и нечетной функции
Произведение четной и нечетной функций есть нечетная функция.
Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)
Значит, \((f\cdot g)(-x)=-(f\cdot g)(x)\) , т.е. функция нечетная.
Исследование функций в примерах
Доказать, что функция \(y=x^2\) четная.
1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.
\(f(x)=f(-x)\) , значит функция четная.
Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)
1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.
\(f(x)\neq f(-x)\) , значит функция не является четной.
\(-f(x)=f(-x)\) , значит функция нечетна.
Исследовать на четность и нечетность функции \(f_1(x)=\frac\) и \(f_2(x)=\frac4\)
Рассмотрим первую функцию:
1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.
Рассмотрим вторую функцию:
1. Найдем область определения: х — любое число кроме -1 и 1. Она симметрична относительно 0.
Разработка содержит теоретический материал, примеры решения задач и задания для самостоятельного решения по теме "Четные и нечетные функции".
Четность и нечетность функции
Функция называется четной , если для любого значения х из ее области определения значение – х также принадлежит области определения и верно равенство f ( ‑ x )= f ( x ).
Область определения четной функции симметрична относительно нуля.
График четной функции симметричен относительно оси Оу .
Функция называется не четной , если для любого значения х из ее области определения значение – х также принадлежит области определения и верно равенство f ( ‑ x )= ‑ f ( x ).
Область определения нечетной функции симметрична относительно нуля.
График нечетной функции симметричен относительно начала координат.

Пример 1 . Дан график функции .
Определите по графику четной или нечетной является функция.
Решение . Поскольку график функции симметричен относительно оси Ох , то функция является четной.
Ответ : функция четная
Задание 1 . Определите по графику четной или нечетной является функция…
1)
2)
3)
4 )
5 )
6 )
7)
8)
9)
10)
Пример 2. На рисунке изображена часть графика некоторой функции, область определения которой - промежуток [ ‑ 4; 4] . Постройте график этой функции, если функция нечетная.

Решение . График нечетной функции симметричен относительно начала координат.
Следовательно, для построения графика нужно отобразить данную часть относительно точки (0; 0):

Задание 2. На рисунке изображена часть графика некоторой функции, область определения которой - промежуток [ ‑ 3; 3] . Постройте график этой функции, если…
1) функция четная

2) функция нечетная

3) функция четная

4) функция нечетная

5) функция четная

6) функция нечетная

7) функция четная

8) функция нечетная

9) функция четная

10) функция нечетная


Пример 3 . Определить четность (нечетность) функции .
Решение . По определению четной функции должно выполняться равенство f ( ‑ x )= f ( x ).
= . Отсюда следует, что функция четная.
Ответ : четная
Задание 3. Определите, является функция четной, нечетной или не является ни четной, ни нечетной…

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

Пример 4. Исследовать функцию на четность (нечетность).
Решение . Подставим в выражение вместо х значение ‑ х : = = . Отсюда следует, что функция нечетная.
Ответ : нечетная
Задание 4. Определите четность или нечетность функции…

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

Пример 5. Вычислите , если f ( x ) – нечетная функция и f ( ‑ 5)=3; f (2)= ‑ 8.
Решение . Поскольку функция f ( x ) – нечетная, то f ( ‑ x )= ‑ f ( x ).

Следовательно, =4( ‑ 3)+8= ‑ 4.
Ответ : ‑ 4
Задание 5 . Вычислите…

1) , если f ( x ) – нечетная функция и f (3)= ‑ 7; f ( ‑ 4)=3

2) , если f ( x ) – четная функция и f (2)=3; f ( ‑ 5)=2

3) , если f ( x ) – четная функция и f (3)= ‑ 7; f ( ‑ 4)=5

4) , если f ( x ) – нечетная функция и f ( ‑ 4)=2; f (2)= ‑ 3

5) , если f ( x ) – нечетная функция и f ( ‑ 3)=1; f (2)= ‑ 3

6) , если f ( x ) – четная функция и f (2)=2; f ( ‑ 3)=3

7) , если f ( x ) – четная функция и f (3)=3; f (5)=2

8) , если f ( x ) – нечетная функция и f ( ‑ 4)=3; f (3)=5

9) , если f ( x ) – нечетная функция и f ( ‑ 3)=3; f (2)= ‑ 3

10) , если f ( x ) – четная функция и f ( ‑ 2)=3; f ( ‑ 5)=4
Сумма двух четных функций четна, а сумма двух нечетных – нечетна.
Произведение двух четных функций является четной функций, произведение двух нечетных функций также является четной функций. Произведение четной и нечетной функции – нечетно.

Если функция f четна (нечетна), то и функция четна (нечетна).

Доказательство : если функция f четна и f ( x ) 0, то .
Если Х симметрично относительно начала координат, то любая заданная на Х функция f является суммой четной и нечетной функций f = g + h , где , .
Доказательство : , . Отсюда следует, что функция g ( x ) четна, а функция h ( x ) нечетна. При этом .
Пример 6 . Функции f и g определены на множестве всех действительных чисел. Является ли функция h четной или нечетной, если h ( x )= f 2 ( x ) g 2 ( x ), f – четная функция, g – нечетная?
Решение . Поскольку f – четная функция, g – нечетная, то f 2 и g 2 – четные функции. Произведение четных функций – функция четная. Следовательно, h ( x )= f 2 ( x ) g 2 ( x ) является четной функцией.
Ответ : четная
Задание 6. Функции f и g определены на множестве всех действительных чисел. Является ли функция h четной или нечетной, если…
Читайте также:

