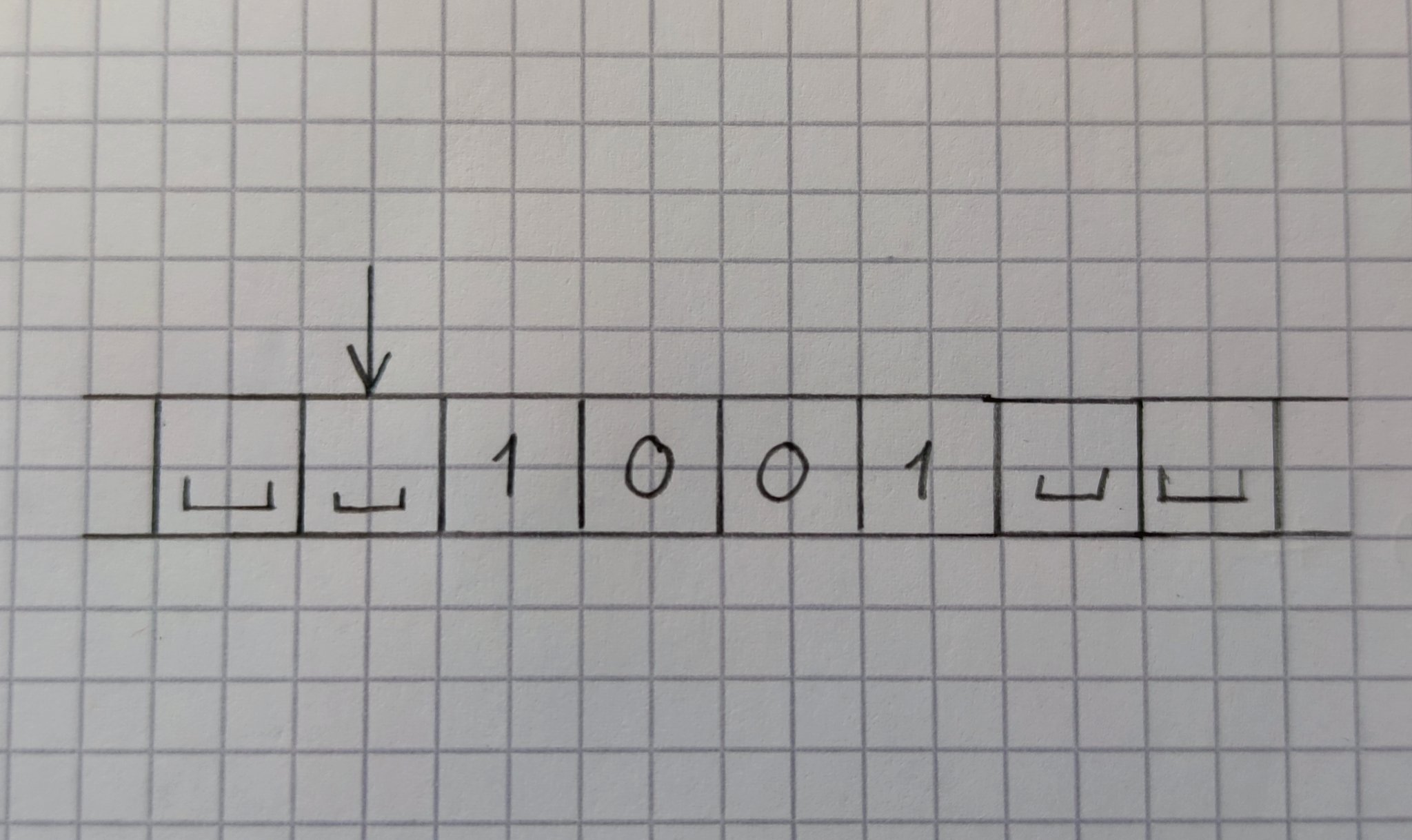Как сделать машину тьюринга

Обновлено: 06.07.2024

Машина Тьюринга — это абстрактный исполнитель или абстрактная вычислительная машина.

Введение

Машина Тьюринга является одним из наиболее выдающихся научных изобретений двадцатого века. Она представляла несложную и удобную абстрактную модель вычислительного процесса, которая представлена в обобщённом формате и позволяет реализовать практически все компьютерные задачи. Простое описание и выполненный математический анализ позволяют считать её фундаментом теоретической информатики.

Эта научная работа послужила стимулом к более углублённому изучению цифрового исчисления и компьютерных устройств, в том числе осознание мысли, что есть проблематика в сфере вычислений, которую нельзя решить на обычных электронных вычислительных машинах пользователей

Машина Тьюринга

Машина Тьюринга была вычислительным модулем, который состоит из сканера для чтения и записи информации с бумажной ленты, пропускаемой через него. Лента поделена на квадратики, несущие один знак, а именно нуль или единицу. Механизм предназначен для ввода и вывода информации и одновременно служит рабочей памятью для сохранения итогов промежуточных вычислительных шагов. Машина имеет в своём составе два компонента:

Лента без ограничений, то есть бесконечная в обоих направлениях лента, разделённая на комплект ячеек.
Автоматический модуль, то есть головка сканера, которая считывает и записывает информацию под управлением программы. Она способна располагаться в любой момент времени лишь в одном из многих состояний.

Готовые работы на аналогичную тему

Машина осуществляет связь двух конечных рядов информационных данных, а именно алфавит знаков на входе $A = (a_0, a_1, …, a_m)$ и алфавит состояний $Q = (q_0, q_1, . q_p)$. Пассивным считается состояние $q_0$. Предполагается, что машина прекращает выполнение операций, когда считывает именно его. Исходным состоянием является состояние $q_1$, и устройство запускается в работу, когда считывает это стартовое состояние. Слово на ленте, которое является входной информацией, расположено последовательно по одной букве в позиции. При этом, впереди него и за ним расположены нулевые квадраты.

Принцип работы машины Тьюринга

Машина Тьюринга принципиально отличается от компьютерных модулей, у неё в качестве запоминающего устройства выступает бесконечная лента, а у цифровых устройств память представляет полосу заданной длины. Любой тип заданий может решить лишь одна сформированная машина Тьюринга. Задания другого класса могут быть решены написанием другого алгоритма. Устройство управления находится в определённом состоянии и способно перемещаться в обе стороны вдоль ленты. Оно может записывать в ячейки и считывать из них алфавитные символы. При перемещении определяется пустой компонент, заполняющий места, которые не содержать входных данных. Алгоритм машины Тьюринга формирует условия перемещений управляющего механизма. Он может задать головке, выполняющей запись и чтение данных, следующие команды:

Записать в текущую ячейку нужный знак.
Выполнить смену текущего состояния.
Переместиться в заданную сторону вдоль ленты.

Машина Тьюринга подобно другим системам, предназначенным для вычислений, обладает определёнными особенностями, которые похожи на свойства алгоритмов:

Свойство дискретности. Цифровое устройство выполняет переход к очередному этапу n+1 лишь после полного завершения предыдущего. Каждый завершенный шаг определяет, каким будет следующий.
Свойство понятности. Машина осуществляет лишь одну операцию для выбранной ячейки. Она записывает алфавитный символ и выполняет одно перемещение в указанную сторону.
Свойство детерминированности. Всем позициям в машине сопоставляется только один вариант осуществления задаваемой схемы, и на всех шагах операции и их очерёдность осуществления строго определены.
Свойство результативности. Окончательный итог на каждом шаге вычисляет машина Тьюринга. Программа работает согласно заданному алгоритму и за не бесконечное количество выполненных этапов доходит до состояния $q_0$.
Свойство массовости. Каждой машине сопоставлен набор допустимых слов, которые входят в алфавит.

Функции машины Тьюринга

Рисунок 1. Функции машины Тьюринга. Автор24 — интернет-биржа студенческих работ

Программа для машины Тьюринга

Программа для машины Тьюринга формируется как таблицы, в которых в первой строчке и столбце находятся знаки внешнего алфавита и набор допустимых внутренних состояний автомата, то есть внутренний алфавит. Данные в таблице, по сути, это команды, которые должна исполнять машина Тьюринга. Разрешение задачи выполняется по следующим правилам. Символ, принятый сканером из ячейки, над которой он располагается в текущий момент, и определённое внутреннее состояние сканера автомата определяют, какую команду требуется исполнить. А именно, это команда, расположенная в таблице, и находящаяся в точке пересечения знаков внутреннего и внешнего алфавита.

Машина Тьюринга (англ. Turing machine) — модель абстрактного вычислителя, предложенная британским математиком Аланом Тьюрингом в 1936 году. Эта модель позволила Тьюрингу доказать два утверждения. Первое — проблема останова неразрешима, т.е. не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте зациклится или прекратит работу. Второе — не существует такой машины Тьюринга, которая способна определить, что другая произвольная машина Тьюринга на её ленте когда-нибудь напечатает заданный символ. В этом же году был высказан тезис Чёрча-Тьюринга, который терминах теории рекурсии формулируется как точное описание интуитивного понятия вычислимости классом общерекурсивных функций. В этой формулировке часто упоминается как просто тезис Чёрча. В терминах вычислимости по Тьюрингу тезис гласит, что для любой алгоритмически вычислимой функции существует вычисляющая её значения машина Тьюринга. В виду того, что классы частично вычислимых по Тьюрингу и частично рекурсивных функций совпадают, утверждение объединяют в единый тезис Чёрча — Тьюринга.

Неформально машина Тьюринга определяется как устройство, состоящее из двух частей:

бесконечной одномерной ленты, разделённой на ячейки,
головки, которая представляет собой детерминированный конечный автомат.

При запуске машины Тьюринга на ленте написано входное слово, причём на первом символе этого слова находится головка, а слева и справа от него записаны пустые символы. Каждый шаг головка может перезаписать символ под лентой и сместиться на одну ячейку, если автомат приходит в допускающее или отвергающее состояние, то работа машины Тьюринга завершается.

Отметим, что существуют различные вариации данного выше определения (например, без отвергающего состояния или с множеством допускающих состояний), которые не влияют на вычислительные способности машины Тьюринга.

Кроме формального определения самой машины требуется также формально описать процесс её работы. В определении для простоты будем предполагать, что головка в процессе работы не записывает на ленту символ [math]B[/math] . Это не ограничивает вычислительной мощности машин Тьюринга, поскольку для каждой машины можно сопоставить аналогичную ей, но не пищущую [math]B[/math] на ленту.

В данной записи головка находится над ячейкой, на которой написана первая буква [math]v[/math] (или [math]B[/math] , если [math]v = \varepsilon[/math] ).

В дальнейшем используются следующие обозначения: [math]x, y, z \in \Pi[/math] , [math]w, v \in \Pi^*[/math]

если [math]\delta(q, x) = \langle p, y, \leftarrow \rangle[/math] , то [math]\langle wz, q, xv \rangle \vdash \langle w, p, zyv \rangle[/math] ,
если [math]\delta(q, x) = \langle p, y, \rightarrow \rangle[/math] , то [math]\langle w, q, xv \rangle \vdash \langle wy, p, v \rangle[/math] ,
если [math]\delta(q, x) = \langle p, y, \downarrow \rangle[/math] , то [math]\langle w, q, xv \rangle \vdash \langle w, p, yv \rangle[/math] .

Особо следует рассмотреть случай переходов по пробельному символу:

Очевидно, что определённое отношение является функциональным: для каждой конфигурации [math]C[/math] существует не более одной конфигурации [math]C'[/math] , для которой [math]C \vdash C'[/math] .

Для машины Тьюринга, которая пишет символ [math]B[/math] на ленту также можно дать аналогичное формальное определение. Оно будет отличаться тем, что символы в строчках конфигурации могут содержать пробелы, и для того, чтобы эти строчки имекли конечную длину, нужно аккуратно учесть наличие пробелов при записи правил перехода.

Машину Тьюринга можно рассматривать как распознаватель слов формального языка. Пусть [math]M[/math] — машина Тьюринга, распознаваемый ей язык определяется как [math]\mathcal L(M) = \< x \in \Sigma^* \mid \exists y, z \in \Pi^*: \langle \varepsilon, S, x \rangle \vdash^* \langle y, Y, z \rangle \>[/math] .

Также можно рассматривать машины Тьюринга как преобразователь входных данных в выходные. Машина [math]M[/math] задаёт вычислимую функцию [math]f[/math] , причём [math]f(x) = y \Leftrightarrow \exists z \in \Pi^* : \langle \varepsilon, S, x \rangle \vdash^* \langle z, Y, y \rangle[/math] . Переход автомата в состояние [math]N[/math] можно интерпретировать как аварийное завершение программы (например, при некорретном входе).

Примеры машин-распознавателей и машин-преобразователей будут даны ниже.

Для начала приведём пример машины-преобразователя, которая прибавляет единицу к числу, записанному на ленте в двоичной записи от младшего бита к старшему. Алгоритм следующий:

в стартовом состоянии головка идёт вправо от младшего бита к старшему, заменяя все единицы на нули,
встретив нуль или пробельный символ головка записывает единицу, после чего переходит в состояние [math]R[/math] ,
в состоянии [math]R[/math] головка идёт влево от старшего бита к младшему, не изменяя символы 0 и 1 на ленте,
встретив в состоянии [math]R[/math] пробельный символ, головка перемещается на один символ вправо и переходит в состояние [math]Y[/math] , завершая работу.

Формально: [math]\Sigma = \[/math] , [math]\Pi = \[/math] , [math]Q = \[/math] . Таблица функции [math]\delta[/math] приведена ниже:

[math]0[/math]	[math]1[/math]	[math]B[/math]
[math]S[/math]	[math]\langle R, 1, \downarrow \rangle[/math]	[math]\langle S, 0, \rightarrow \rangle[/math]	[math]\langle R, B, \leftarrow \rangle[/math]
[math]R[/math]	[math]\langle R, 0, \leftarrow \rangle[/math]	[math]\langle R, 1, \leftarrow \rangle[/math]	[math]\langle Y, B, \rightarrow \rangle[/math]

В качестве примера машины-распознавателя приведём машину, распознающую палиндромы над алфавитом [math]\[/math] . Алгоритм следующий:

если строка на ленте — пустая, то перейти в допускающее состояние
надо запомнить первый символ слова в состоянии автомата,
стереть его,

перейти в конец ленты:

если оставшаяся строка на ленте — пустая, то перейти в допускающее состояние
если последний символ совпадает с запомненным, стереть его, перейти в начало ленты и повторить с первого шага
в случае несовпадения перейти в отвергающее состояние

Формально: [math]\Sigma = \[/math] , [math]\Pi = \[/math] , [math]Q = \[/math] . Таблица функции [math]\delta[/math] приведена ниже:

[math]0[/math]	[math]1[/math]	[math]B[/math]
[math]S[/math]	[math]\langle F_0, B, \rightarrow \rangle[/math]	[math]\langle F_1, B, \rightarrow \rangle[/math]	[math]\langle Y, B, \downarrow \rangle[/math]
[math]F_0[/math]	[math]\langle F_0, 0, \rightarrow \rangle[/math]	[math]\langle F_0, 1, \rightarrow \rangle[/math]	[math]\langle B_0, B, \leftarrow \rangle[/math]
[math]F_1[/math]	[math]\langle F_1, 0, \rightarrow \rangle[/math]	[math]\langle F_1, 1, \rightarrow \rangle[/math]	[math]\langle B_1, B, \leftarrow \rangle[/math]
[math]B_0[/math]	[math]\langle R, B, \leftarrow \rangle[/math]	[math]\langle N, 1, \downarrow \rangle[/math]	[math]\langle Y, B, \downarrow \rangle[/math]
[math]B_1[/math]	[math]\langle N, 0, \downarrow \rangle[/math]	[math]\langle R, B, \leftarrow \rangle[/math]	[math]\langle Y, B, \downarrow \rangle[/math]
[math]R[/math]	[math]\langle R, 0, \leftarrow \rangle[/math]	[math]\langle R, 1, \leftarrow \rangle[/math]	[math]\langle S, B, \rightarrow \rangle[/math]

В этом разделе приведены различные варианты машин Тьюринга, которые не отличаются от обычных машин Тьюринга по вычислительной мощности.

Машиной Тьюринга с [math]n[/math] дорожками называется вычислитель, аналогичный машине Тьюринга, лишь с тем отличием, что лента состоит из [math]n[/math] дорожек, на каждой из которых записаны символы ленточного алфавита. У многодорожечной машины одна головка, которая за один шаг переходит в одном направлении на всех дорожках одновременно. Соответственно, функция перехода имеет тип [math]\delta : Q \times \Pi^n \to Q \times \Pi^n \times \<\leftarrow, \rightarrow, \downarrow\>[/math] . Многодорожечная машина Тьюринга тривиально эквивалентна обычной с ленточным алфавитом [math]\Pi' = \Pi^n[/math] .

Заменив у машины Тьюринга бесконечную в обе стороны ленту на бесконечную в одну сторону, мы не теряем в вычислительной мощности. По произвольной машине Тьюринга строится двухдорожечная машина с полубесконечной лентой.

Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте.

Существует алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Сначала занумеруем ячейки рабочей ленты машины Тьюринга с бесконечной лентой следующим образом:

Затем перенумеруем ячейки, и запишем символ [math]c \in \Pi \setminus \Sigma, B[/math] в начало ленты, который будет означать границу рабочей зоны:

Наконец, изменим машину Тьюринга, удвоив число её состояний, и изменим сдвиг головки так, чтобы в одной группе состояний работа машины была бы эквивалентна её работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе машины Тьюринга встретится символ [math]c[/math] , значит головка достигла границы рабочей зоны:

В отличие от многодорожечной машины Тьюринга, ленты не зависят друг от друга и головки во время одного шага могут перемещаться по-разному. То есть, функция перехода теперь имеет тип [math]\delta : Q \times \Pi^n \to Q \times \Pi^n \times \<\leftarrow, \rightarrow, \downarrow\>^n[/math] .

Многоленточная машина с [math]n[/math] дорожками эмулируется многодорожечной машиной с [math]2n[/math] дорожками следующим образом: каждая нечётная дорожка соответствует ленте исходной машины, а на каждой чётной дорожке отмечены специальным символом [math]*[/math] позиция головки на ленте выше (считаем, что ленты нумеруются сверху вниз).

Каждый шаг исходной машины эмулируется конечной последовательностью шагов построенной машины следующим образом: исходно головка находится в позиции самой левой отметки и идёт вправо до самой правой отметки, запоминая прочитанные около символов [math]*[/math] символы в состоянии. Пройдя до самой правой отметки, головка возвращается влево, совершая необходимые действия (переписывая символы около отметок и передвигая сами отметки). После такого прохода головка переходит в следующее состояние, завершая эмуляцию шага.

Аланом Тьюрингом было сформулировано следующее утверждение:

Иными словами, тезис говорит о том, что любой алгоритм можно запрограммировать на машине Тьюринга.

Существует машина Тьюринга, которая принимает на вход закодированное описание произвольной машины и входную строку и эмулирует работу закодированной машины на заданном входном слове. Иными словами, универсальный язык перечислим с помощью машины Тьюринга. Ссылки на явные конструкции универсальных машин Тьюринга приведены ниже.

В 30-е годы XX века английский математик Алан Тьюринг придумал такое странное устройство, которое теперь называют машиной Тьюринга.

Идея его была в том, чтобы придумать устройство, абстрактную машину, которая может делать все, что вообще могут делать машины. Он был не единственным в этот момент, другие люди тоже в других терминах определяли похожие вещи, но в гораздо более абстрактных терминах, по крайней мере, в их работах конкретного механизма работы машины не было.

Оказалось же, что это одно из самых важных открытий XX века. То, что сейчас в разных устройствах — скажем, в телевизоре и в стиральной машине, — может использоваться одна и та же микросхема процессора, — это воплощение одной из идей Тьюринга.

И то, что одна и та же программа может использоваться в самых разных компьютерах, работать с самой разной аппаратурой и выглядеть одинаково, это тоже его идея. Тогда это называлось идеей хранимой программы (программа хранится в памяти и определяет поведение машины), и ещё была идея универсальной машины, — есть машина, которая может делать все, что может делать любая другая машина.

Если бы не Тьюринг, наверно, это придумал бы кто-то другой, он не был единственным, кто над этим работал, но так или иначе такое абстрактное теоретическое устройство оказалось одним из самых важных изобретений в XX веке.

Интересно, что потом Тьюринг, когда настали трудные времена, не только занимался теорией, но и практически участвовал в разных важных проектах.

А после войны Тьюринг уже строил реальную электронную вычислительную машину. Хотя прямой связи с его теоретическими работами не было, но явно это было продолжением той же самой деятельности. Так что хорошая теория — вещь очень практичная, и не надо бояться того, что теоретические работы окажутся бесполезными.

Сейчас это большая наука, которая называется теория сложности вычислений, в ней много всего интересного открыли, но есть самая главная проблема, которая называется проблема перебора, и которая до сих пор не решена.

Ее можно объяснить на таком примере: выпускалась игрушка Eternity — это такая коробочка, в которую уложены плитки, раскрашенные в разные цвета, но они раскрашены так, что видно, какие плитки можно прикладывать друг к другу (там рисунок на краях). Продаются они рассыпанными, и фирма, которая их изготовила, утверждает, что все это можно собрать в одну картинку внутри этой квадратной коробки (там 256 плиток) — то есть что изначально это была одна картинка, разрезанная на плитки.

По современным представлениям, машины такие задачи за обозримое время решать не могут, никакого способа, кроме как перебирать все варианты (а их очень много) сейчас не известно. Но, с другой стороны, никто этого не может и доказать. Это и называется проблемой перебора — доказать, что такой полный перебор каких-то объектов нельзя заменить никаким более коротким вычислением.

Так вот, первая проблема в этом списке — это проблема перебора, и она там заслуженно. Интересно в теории сложности вычислений то, что не только наличие какого-то алгоритма полезно практически, но, как ни странно, часто бывает полезно отсутствие алгоритма.

Например, есть такой известный вопрос о разложении чисел на множители. Если число небольшое, то легко проверить, что оно простое — можно проверить все меньшие числа, и понять, что там нет делителей. Если число большое, то так просто уже нельзя проверить — но существуют разные алгоритмы, которые позволяют это делать. (Они основаны на малой теореме Ферма и её усовершенствованиях, но это отдельная тема.)

Так или иначе, алгоритмы проверки простоты существуют. А теперь другая задача: возьмём два больших простых числа и их перемножим, сообщим, что у нас получилось, и спросим, какие это были числа. Это задача разложения на множители, и никто не знает, как это быстро сделать. И то, что этого никто не знает, очень хорошо, потому что благодаря этому существует вся вычислительная криптография, это одно из основных её предположений.

Когда кто-нибудь снимает деньги в банке, или в Интернете заходит на сайт с помощью SSL — используются системы криптографии, основанные на том, что быстро разлагать на множители числа нельзя. Если кто-нибудь в какой-то момент обнаружит, что разлагать можно, то, думаю, после этого будет экономический кризис, потому что вся банковская система рухнет, пока люди не заменят это чем-то другим (вообще без использования компьютеров или с какими-то новыми алгоритмами).

Так что отсутствие алгоритма может быть полезнее, чем его наличие. К сожалению, никто не может доказать, что алгоритма нет, хотя все подозревают, что это так — не решена ни общая проблема перебора, ни этот частный ее случай (разложение чисел на множители), особенно важный, и про него тоже все думают, но никто ничего не придумал.

Что такое случайность? Это дело тонкое, вообще, существует ли случайность? Когда в каком-нибудь казино играют в рулетку — может ли наука предсказать, что там выпадет, и как нужно играть, чтобы выиграть, или это в принципе невозможно?

Федор Михайлович Достоевский твердо верил, что если быть хладнокровным и не волноваться во время игры, то можно выиграть, — он говорил, что, к сожалению, ему не удаётся быть хладнокровным, и поэтому он всё время проигрывал.

С другой стороны, теория вероятностей основана на том, что такой системы не существует, что последовательность бросания монеты в какой-нибудь игре, или последовательность выпадения красного и черного в рулетке, случайны и непредсказуемы. Но возникает вопрос, что такое случайность? Как определить, что это значит? Можем ли мы отделить случайное от неслучайного?

Сейчас вы видите две последовательности:

Вам сказано, что одна из них получена бросанием монеты, а другая как-то иначе. Сможете ли вы определить, какая из них получена каким образом?

Я думаю, что сможете, и что более-менее всякий человек, который посмотрит на эту картинку, скажет, что первая последовательность получена не бросанием монеты, а просто чередованием 0 и 1, а вторая вполне может быть получена бросанием монеты.

Время от времени он из пачки сделанных колод достаёт одну колоду, распаковывает и смотрит, хорошо ли она перетасована. С одной стороны, он должен что-то контролировать, то есть если он никогда никакие колоды не будет браковать как негодные, то зачем он вообще нужен? А с другой стороны, непонятно, что он может контролировать, потому что вся идея того, что карты хорошо перетасованы, состоит в том, что все варианты, все возможные последовательности карт в колоде, имеют совершенно одинаковую вероятность.

Соответственно, ни одна из них, с точки зрения тасовальной машины, не лучше другой. Почему же мы некоторые колоды (некоторые последовательности карт) бракуем, а некоторые оставляем? Это как-то загадочно.

Если, скажем, все карты идут в порядке возрастания их значения, или сначала идут все красные карты, а потом черные — такие комбинации, вроде бы, надо браковать. Но, с другой стороны, непонятно, чем они хуже других. Одной из попыток ответить на этот вопрос (60-е годы XX века) было понятие сложности, то, что сейчас называется колмогоровская сложность или алгоритмическая сложность.

Идея эта совсем простая — что первая из последовательностей

А для настоящей случайной монеты (как считается в рамках этого объяснения случайности) — никакого способа описать последовательность более коротким способом, чем показав просто все нули и единицы, как они есть, не существует.

В этом и состоит основная идея Колмогорова и его коллег, которые придумали, что сложность последовательности — это длина кратчайшей программы, которая такую последовательность может напечатать, а случайные последовательности отличаются от неслучайных тем, что нельзя их напечатать никакой программой, которая короче, чем сама последовательность.

Теперь целая наука на эту тему возникла, она называется алгоритмическая теория информации, алгоритмическая случайность, но, конечно, многие вопросы там еще не ясны. Не ясен вопрос о том, что можно сделать с ограничением на сложность вычислений.

Возможно, что последовательность на самом деле неслучайна и имеет какое-то короткое описание, но мы его просто не знаем и не можем найти — или проблема может быть не в том, что мы его не можем найти, а в том, что для того, чтобы восстановить последовательность по этому описанию, нужно очень много времени.

Вот это такая активно развивающаяся и, к сожалению, ещё не очень развитая область, и там, может быть, что-нибудь интересное в ближайшее время (или не в ближайшее время) откроют.

Если вы хотите получать больше статей, подобно этой, то кликните Recommend ниже.

Open with Desktop
View raw
Copy raw contents Copy raw contents

Copy raw contents

Абстрактные вычислительные машины

Материал взят с ресурса Планета информатики

Машина Тьюринга - абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.

Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча - Тьюринга, способна имитировать всех исполнителей (с помощью задания правил перехода), каким-либо образом реализующих процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.

То есть, всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.

Машина Тьюринга состоит из бесконечной в обе стороны ленты, разделенной на ячейки, и автомата (головки), которая управляется программой. Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице.

Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:

Внешний алфавит. Конечное множество (например, А ), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, Q0 ) должна представлять собой пустой символ.
Внутренний алфавит. Конечное множество состояний головки (автомата). Одно из состояний (например, Q1 ) должно быть начальным (запускающим программу). Еще одно из состояний ( Q0 ) должно быть конечным (завершающим программу) – состояние останова.
Таблица переходов. Описание поведения автомата (головки) в зависимости от состояния и считанного символа.

Автомат машины Тьюринга в процессе своей работы может выполнять следующие действия:

Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой).
Передвигаться на одну ячейку влево или вправо.
Менять свое внутреннее состояние.

Одна команда для машины Тьюринга как раз и представляет собой конкретную комбинацию этих трех составляющих: указаний, какой символ записать в ячейку (над которой стоит автомат), куда передвинуться и в какое состояние перейти. Хотя команда может содержать и не все составляющие (например, не менять символ, не передвигаться или не менять внутреннего состояния).

Можно усложнить программу. Допустим, головка располагается не обязательно над первым, а над любым символом слова. Тогда программа для данной машины Тьюринга может быть такой (а могла бы быть и другой):

Здесь происходит сдвиг головки влево до тех пор, пока она не окажется над пустым символом. После этого машина переходит в состояние Q2 (команды которого совпадают с командами Q1 предыдущей программы).

Материал взят с ресурса Планета информатики

На ленте машины Тьюринга содержится последовательность символов + . Напишите программу для машины Тьюринга, которая каждый второй символ + заменит на - . Замена начинается с правого конца последовательности. Автомат в состоянии Q1 обозревает один из символов указанной последовательности. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Дано число n в восьмеричной системе счисления. Разработать машину Тьюринга, которая увеличивала бы заданное число n на 1 . Автомат в состоянии Q1 обозревает некую цифру входного слова. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Дана десятичная запись натурального числа n > 1 . Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1 . Автомат в состоянии Q1 обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Дано натуральное число n > 1 . Разработать машину Тьюринга, которая уменьшала бы заданное число n на 1 , при этом в выходном слове старшая цифра не должна быть 0 . Например, если входным словом было 100 , то выходным словом должно быть 99 , а не 099 . Автомат в состоянии Q1 обозревает правую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Дан массив из открывающих и закрывающих скобок. Построить машину Тьюринга, которая удаляла бы пары взаимных скобок, т.е. расположенных подряд ( ) . Например, дано ) ( ( ) ( ( ) , надо получить ) . . . ( ( . Автомат в состоянии Q1 обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Дана строка из букв a и b . Разработать машину Тьюринга, которая переместит все буквы a в левую, а буквы b - в правую части строки. Автомат в состоянии Q1 обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

На ленте машины Тьюринга находится число, записанное в десятичной системе счисления. Умножить это число на 2 . Автомат в состоянии Q1 обозревает крайнюю левую цифру числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Даны два натуральных числа m и n , представленные в унарной системе счисления. Соответствующие наборы символов | разделены пустой клеткой. Автомат в состоянии Q1 обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит сумму чисел m и n . Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Даны два натуральных числа m и n , представленных в унарной системе счисления. Соответствующие наборы символов | разделены пустой клеткой. Автомат в состоянии Q1 обозревает самый правый символ входной последовательности. Разработать машину Тьюринга, которая на ленте оставит разность чисел m и n . Известно, что m > n . Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

На ленте машины Тьюринга находится десятичное число. Определить, делится ли это число на 5 без остатка. Если делится, то записать справа от числа слово да , иначе - нет . Автомат обозревает некую цифру входного числа. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

В состоянии Q1 машина ищет правый конец числа, в состоянии Q2 - пропускает знак + , при достижении конца последовательности - останавливается. В состоянии Q3 машина знак + заменяет на знак - , при достижении конца последовательности она останавливается.

Решение этой задачи аналогично рассмотренному выше примеру.

Состояние Q1 - уменьшаем младшую (очередную) цифру на 1 . Если она не равна нулю, то после уменьшения сразу - останов, если же младшая цифра равна 0 , то вместо нее пишем 9 , смещаемся влево и вновь выполняем вычитание. В клетку [ A0 , Q1 ] машина Тьюринга никогда не попадет, поэтому ее можно не заполнять.

Задача 4 (усложнение задачи 3)

Состояние Q1 - уменьшаем младшую (очередную) цифру на 1 . Если она больше 1 , то после уменьшения - сразу останов, если же младшая цифра равна 0 , то вместо нее пишем 9 , смещаемся влево и вновь выполняем вычитание. Если уменьшаемая цифра равна 1 , то вместо нее пишем 0 и переходим в состояние Q2 .

Состояние Q2 - после записи 0 в каком-либо разряде надо проанализировать, не является ли этот ноль старшей незначащей цифрой (т.е. не стоит ли слева от него в записи выходного слова A0 ).

Состояние Q3 - если записанный 0 является старшей незначащей цифрой, то его надо удалить из записи выходного слова.

Те клетки, в которые машина Тьюринга никогда не попадает, оставляем пустыми.

Состояние Q1 : если встретили ( , то сдвиг вправо и переход в состояние Q2 ; если встретили A0 , то останов.

Состояние Q2 : анализ символа ( на парность, в случае парности должны увидеть ). Если парная, то возврат влево и переход в состояние Q3 .

Состояние Q3 : стираем сначала ( , затем ) и переходим в Q1 .

Решение этой задачи обычно вызывает у школьников затруднение. При разборе решения этой задачи можно пойти, например, следующим путем.

Рассмотрите со школьниками следующие варианты входных слов и попросите их сформулировать, что должна делать машина Тьюринга, каков внешний вид выходного слова, чем с точки зрения машины Тьюринга эти варианты различаются:

aaa -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

a -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

bbb -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

b -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

ab -> выходное слово совпадает с входным, просматриваем входное слово до тех пор, пока оно не заканчивается.

Результат обсуждения. Машина Тьюринга должна "понимать", по цепочке каких букв она идет, т.е. у нее должно быть как минимум два состояния. Пусть состояние Q1 - движение по цепочке из букв a , а Q2 - состояние движения по цепочке из букв b . Заметим, что цепочка может состоять и из одной буквы. Если мы дошли до конца строки в состоянии Q1 или Q2 , т.е. встретили A0 , машина должна остановиться, мы обработали всю строку.

Рассмотрим следующие варианты входных слов:

Результат обсуждения. Первый вариант входного слова можно последовательно обработать следующим образом: bba -> bbb -> вернуться к левому концу цепочки из букв b -> abb (заменить первую букву в этой цепочке на a ). Для выполнения этих действий нам потребуется ввести два новых состояния и, кроме того, уточнить состояние Q2 . Таким образом, для решения этой задачи нам нужно построить машину Тьюринга со следующими состояниями:

Q1 - идем вправо по цепочке букв a . Если цепочка заканчивается A0 , то переходим в Q0 ; если заканчивается буквой b , то переходим в Q2 ;

Q2 - идем вправо по цепочке букв b , если цепочка заканчивается A0 , то переходим в Q0 ; если заканчивается a , то заменяем букву a на b , переходим в состояние Q3 (цепочку вида заменили на цепочку вида );

Q3 - идем влево по цепочке букв b до ее левого конца. Если встретили A0 или a , то переходим в Q4 ;

Q4 - заменяем b на a и переходим в Q1 (цепочку вида заменяем на цепочку вида .

состояние Q1 - поиск правой (младшей) цифры числа;

состояние Q2 - умножение очередной цифры числа на 2 без прибавления 1 переноса;

состояние Q3 - умножение очередной цифры числа на 2 с прибавлением 1 переноса.

Машина Тьюринга для этой программы выглядит тривиально просто - в ней всего одно состояние. Такая машина Тьюринга выполняет следующие действия: стирает самый правый штрих, ищет разделитель (пустую ячейку) и в эту пустую ячейку помещает штрих, тем самым сформирована непрерывная последовательность штрихов длины n + m .

Однако, как ни странно, решение этой задачи вызывает большие трудности. Очень часто ученики строят машину Тьюринга, которая выполняет циклические действия: последовательно пододвигают правые n штрихов к левым.

В этом случае их программа выглядит следующим образом:

состояние Q1 - поиск разделителя;

состояние Q2 - передвинули штрих;

состояние Q3 - проверка на конец (все ли штрихи передвинули).

На примере этой задачи четко видно, как часто дети пытаются решить задачу уже знакомыми способами. Мне кажется, что, предлагая ученикам задачи на составление машин Тьюринга, мы развиваем способность к нахождению необычных решений, развиваем способность творчески думать!

Эта задача кажется школьникам достаточно легкой, но трудности возникают с остановом машины Тьюринга. Ниже приведен один из возможных вариантов машины Тьюринга для этой задачи.

Идея решения (условие останова). На ленте есть два исходных массива штрихов.

Штрихи начинаем стирать с левого конца массива m . И поочередно стираем самый левый штрих в массиве m и самый правый штрих в массиве n . Но прежде чем стереть правый штрих в массиве n , проверяем, единственный он (т.е. последний, который надо стереть) или нет.

Опишем сначала состояния машины Тьюринга, которые необходимы для решения нашей задачи, а затем составим программу-таблицу.

Состояние Q1 - поиск разделителя между массивами штрихов при движении справа налево;

состояние Q2 - поиск левого штриха в массиве m ;

состояние Q3 - удаление левого штриха в массиве m ;

состояние Q4 - поиск разделителя при движении слева направо;

состояние Q5 - поиск правого штриха в массиве n ;

состояние Q6 - проверка единственности этого штриха в массиве n , т.е. определяем, был ли он последним;

состояние Q7 - если он был последним, то останов, иначе переход на новый цикл выполнения алгоритма.

При решении этой задачи следует обратить внимание на правильное выписывание алфавита:

Состояние Q1 - поиск правого конца числа;

состояние Q2 - анализ младшей цифры числа; если она равна 0 или 5 , т.е. число делится на 5 , то переход в состояние Q3 , иначе переход в состояние Q5 ;

состояние Q3 - запись буквы Д справа от слова на ленте;

состояние Q4 - запись буквы А справа от слова и останов машины;

состояние Q5 - запись буквы Н справа от слова;

состояние Q6 - запись буквы Е справа от слова;

состояние Q7 - запись буквы Т справа от слова и останов машины.

Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на ячейки бесконечной в обе стороны ленты. Каждая ячейка ленты может находиться в 2 состояниях - быть либо пустой - 0 , либо помеченной меткой 1 . За такт работы машины каретка может сдвинуться на одну позицию влево или вправо, считать, изменить символ в своей текущей позиции.

Работа машины Поста определяется программой, состоящей из конечного числа строк. Для работы машины нужно задать программу и её начальное состояние (то есть состояние ленты и позицию каретки). Кареткой управляет программа, состоящая из пронумерованных не обязательно упорядоченных строк команд, если в каждой команде указана строка, на которую нужно перейти. Обычно принимается, что если в команде переход не указан, то переход происходит на следующую строку. Каждая команда имеет следующий синтаксис:

где i - номер команды, K - действие каретки, j - номер следующей команды (отсылка). Всего для машины Поста существует шесть типов команд:

После программы запуска возможны варианты:

работа может закончиться невыполнимой командой (стирание несуществующей метки или запись в помеченное поле);
работа может закончиться командой "стоп";
работа никогда не закончится.

Для сложения и вычитания натуральных (целых неотрицательных) чисел P и Q их можно представить на ленте набором из P единиц и Q , отделённых друг от друга одним нулём; пусть исходное положение каретки находится на крайней левой 1 группы единиц Q :

Сложение двух чисел тривиально - достаточно поставить 1 между числами и стереть одно крайнее правое 1 у представления Q .

Программа вычитания таких чисел состоит из последовательного изменения крайних левых 1 у представления Q и правых 1 у представления P . В начале программы каретка установлена на крайнюю левую 1 у Q :

- шаг влево
? 1; 3 - если в ячейке пусто, перейти к 1 -шагу, если нет - к 3
X - удалить метку
-> - шаг вправо
? 4; 6 - если в ячейке пусто, перейти к 4 -шагу, если нет - к 6
X - удалить метку
-> - шаг вправо
? 9; 1 - если в ячейке пусто, перейти к 9 шагу, если нет - к 1
! - конец В 5 -й строке возможно зацикливание, если Q > P .

You can’t perform that action at this time.

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session.

Разработчик программного обеспечения Валерий Жила объяснил, как устроены машины Тьюринга. По его словам, когда он начинал разбираться с этой концепцией, у него разболелась голова. Теперь же специалист считает, что в ней нет ничего сложного. Что это за машины и зачем они нужны, разработчик максимально просто объяснил в треде.

Примечание: машина Тьюринга (МТ) — это абстракция из мира Computer Science, которой не существует в физическом мире.

Обычная машина Тьюринга состоит из трех частей, из которых первые две технические, а в третьей, по словам Валерия, происходит магия. Они называются:

Указатель

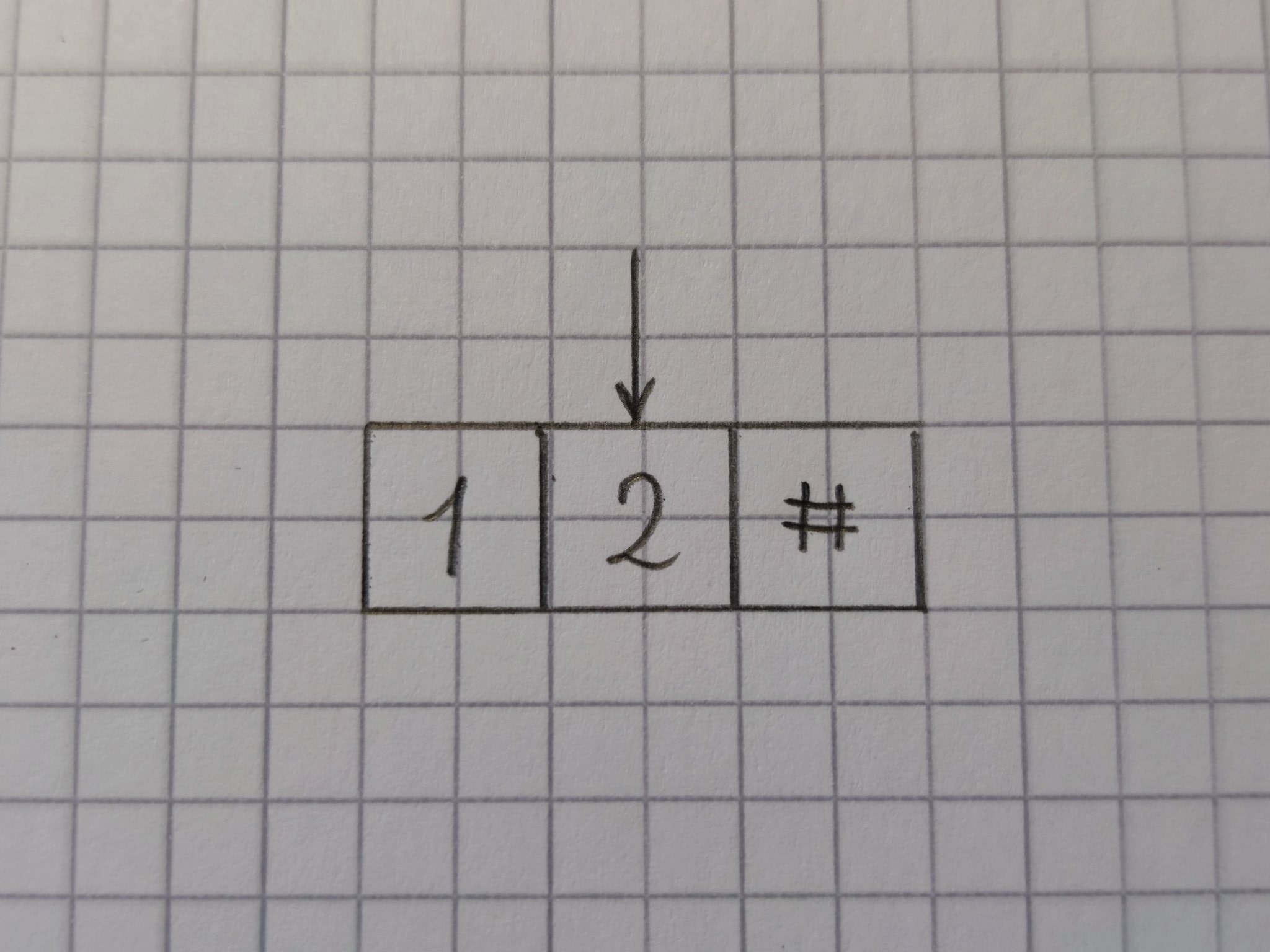
Указатель обозначается стрелкой, как показано на рисунке ниже, и всегда указывает на одну ячейку. Этот элемент может следующее:

считывать содержимое ячейки;
записать что-то в нее;
перемещаться.

Указатель может двигаться тремя способами:

на одну ячейку влево;
на одну ячейку вправо;
стоять на месте.

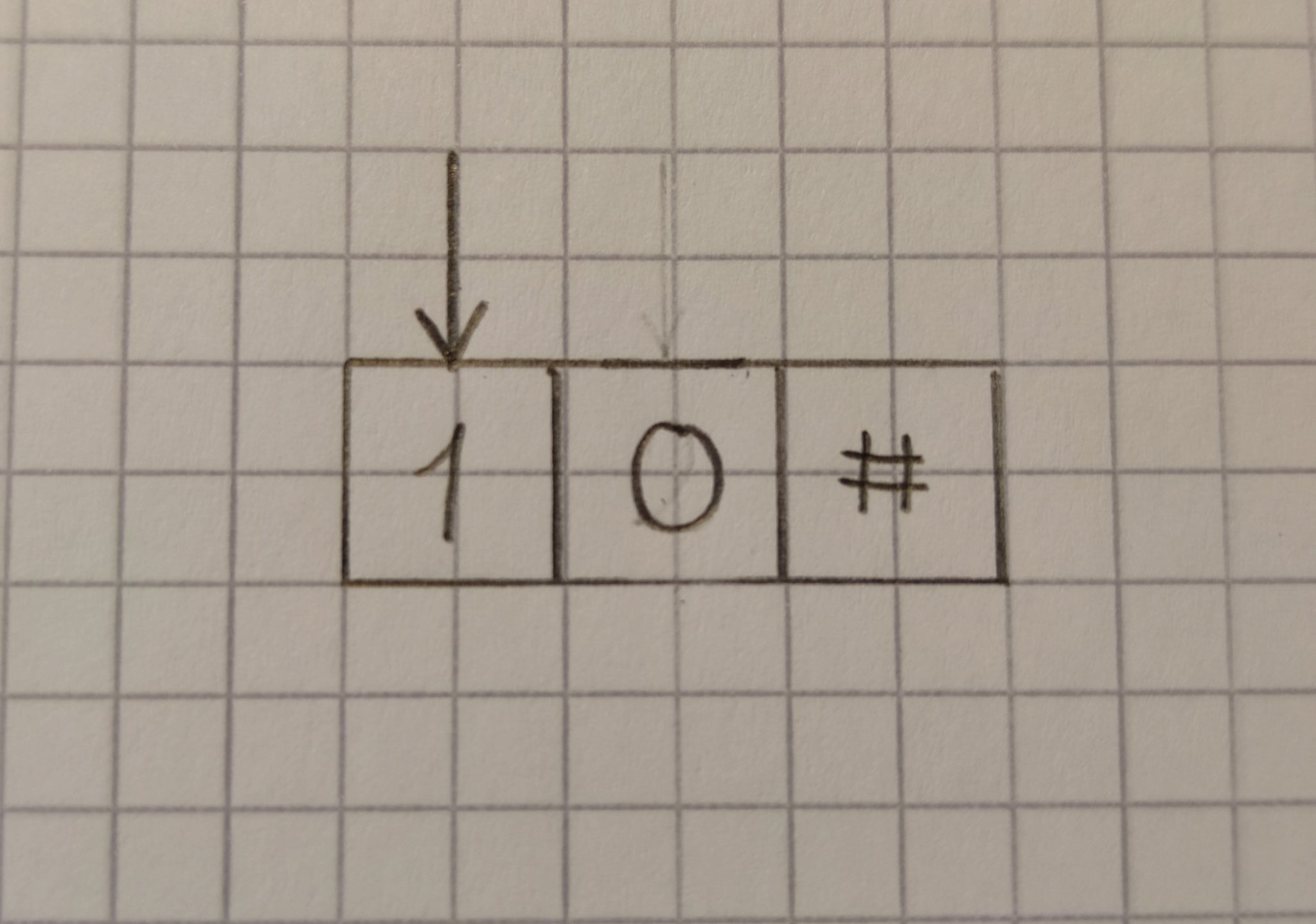
Запишем в ячейку ноль и переместим указатель на одну ячейку влево. Вот что получится:

Все действия машин строятся следующим образом:

читаем ячейку;
что-то пишем в ней — в зависимости от программы или прочитанного;
перемещаемся.

Вышеописанное действие можно описать как (2,0,L), то есть: читаем два, пишем ноль, едем влево.

Движение часто обозначают так:

L (Left) — едем влево;
N (None) — стоим на месте;
R (Right) — едем вправо.

Бесконечная лента

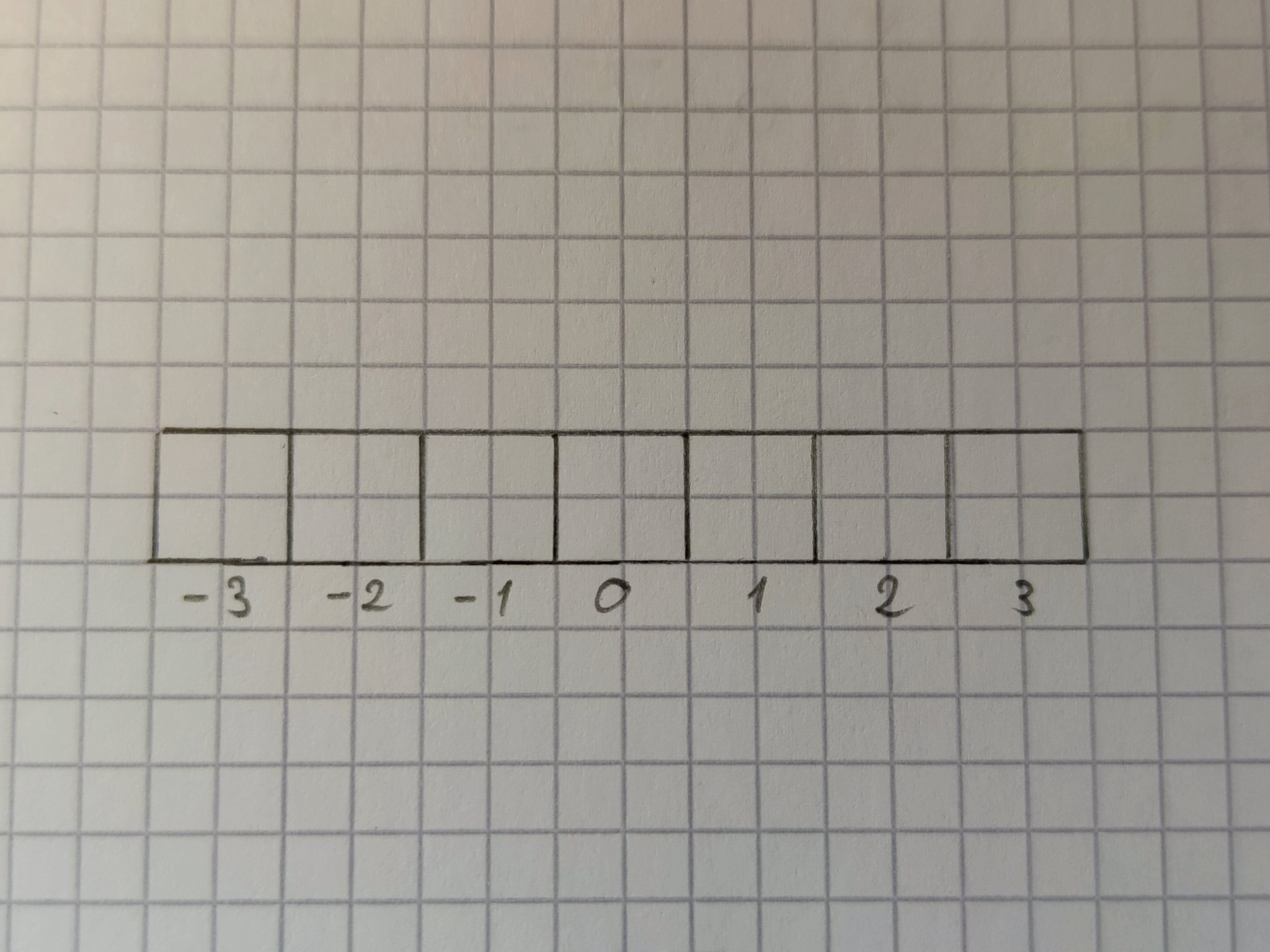
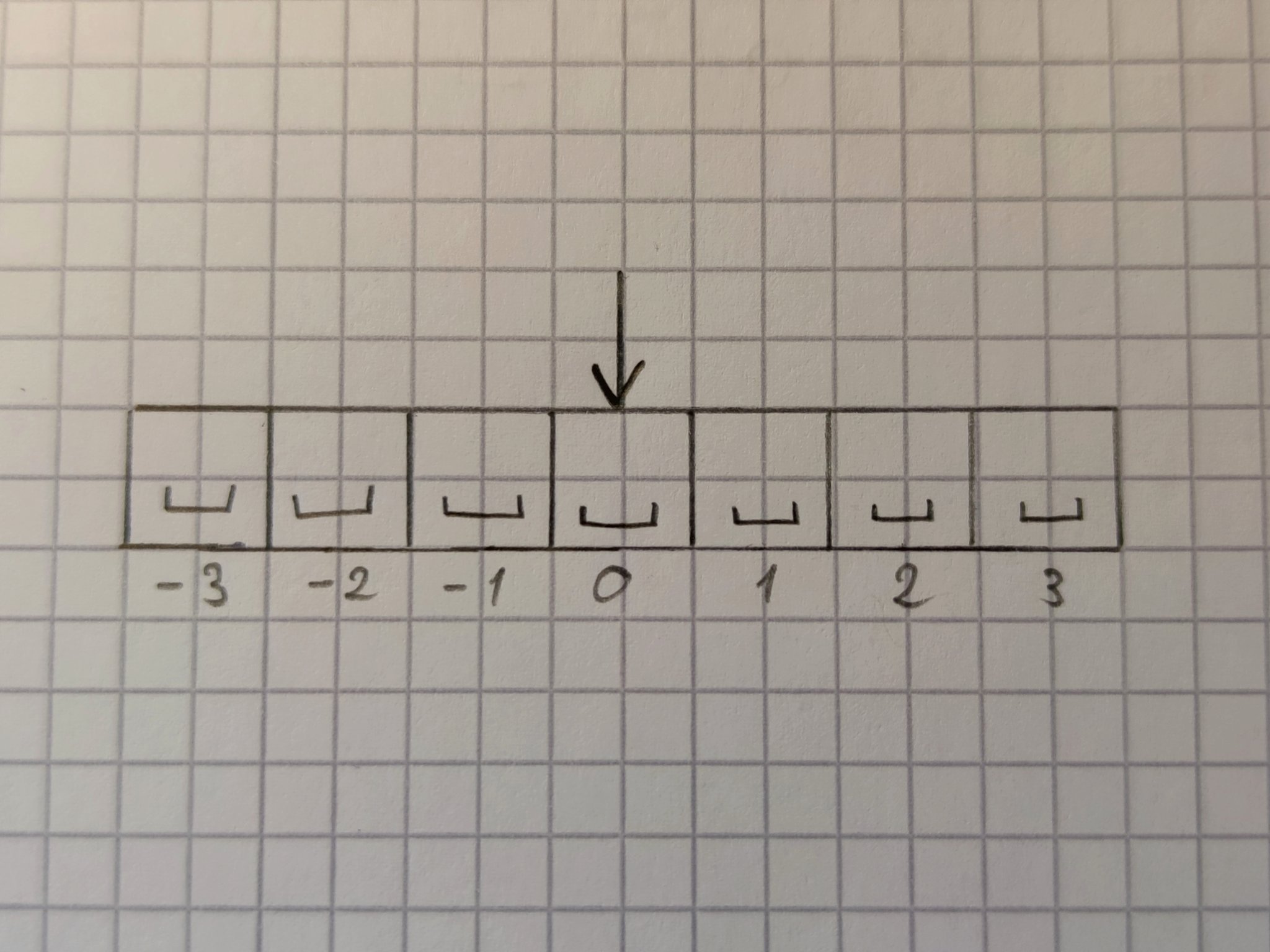
В примере выше была лента из трех ячеек. Этого мало. Давайте рассмотрим из семи. Автор пронумеровал их от -3 до 3.

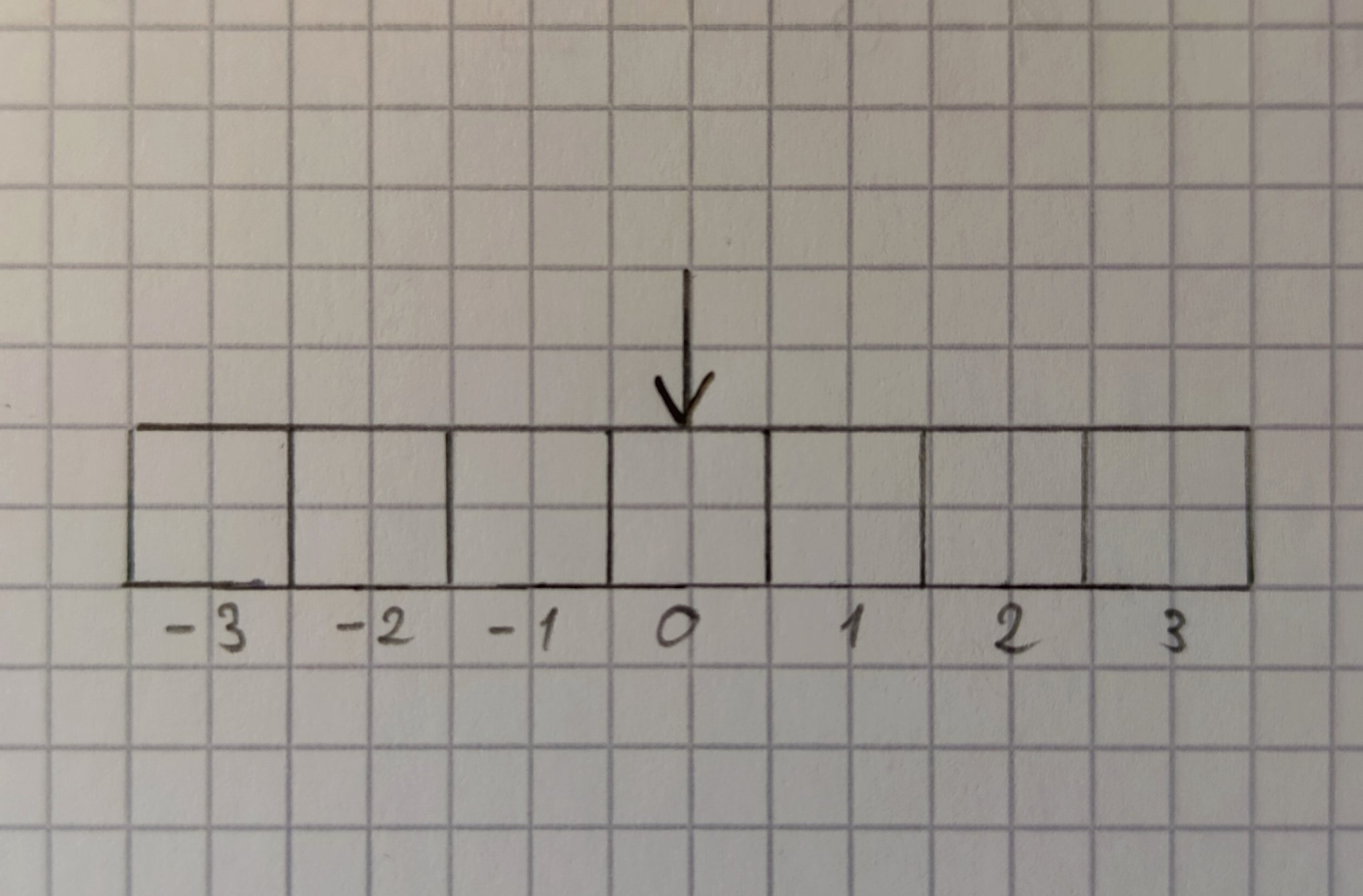
Примем за правило, что при запуске машины указатель всегда находится над ячейкой под номером 0.

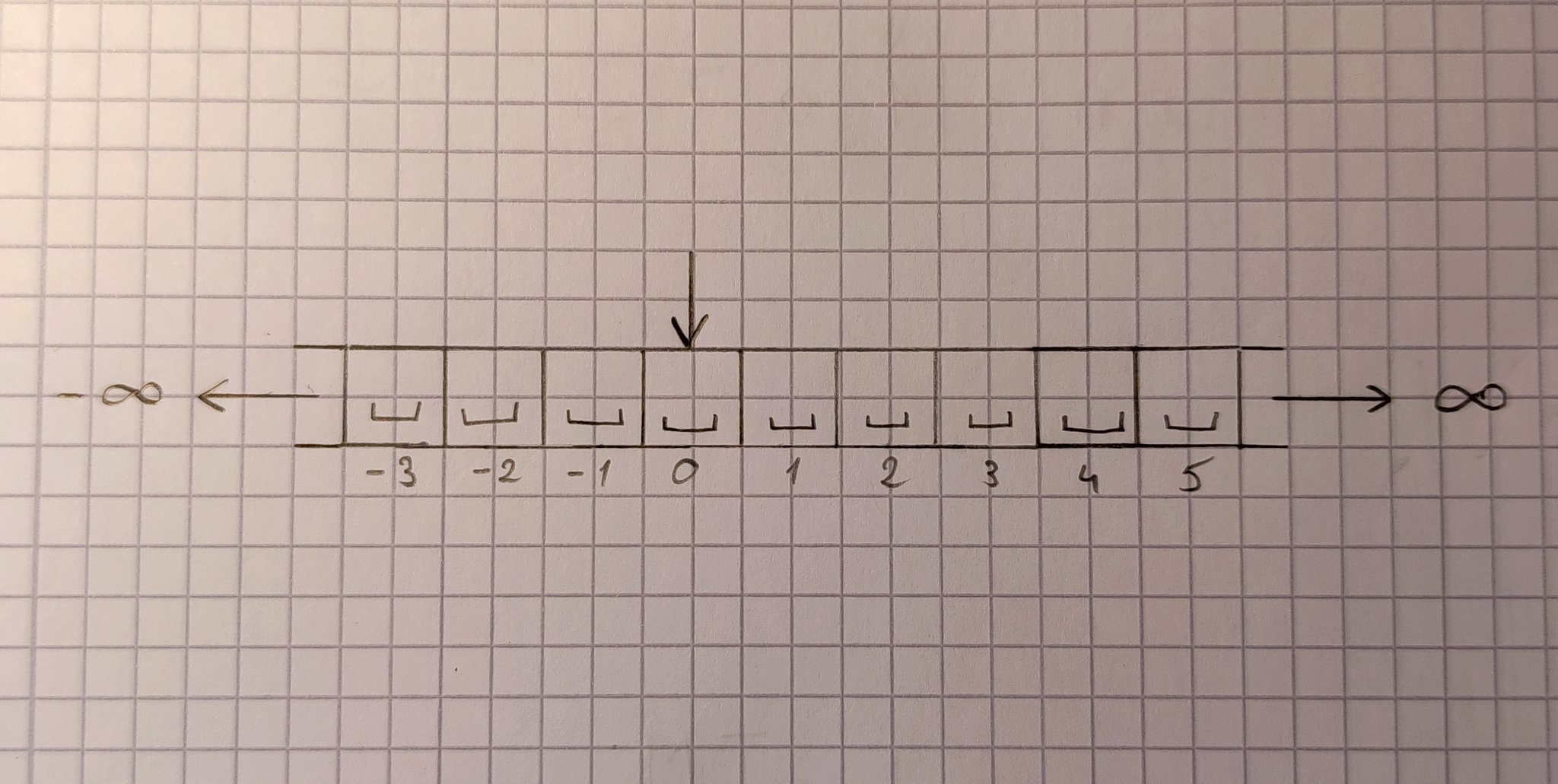
Лента машины Тьюринга похожа на вышеописанную, но состоит не из семи ячеек, а бесконечна направо и налево. Так как в МТ нет никакой нумерации, достаточно того, что при запуске указатель находится в середине ленты, поэтому можно бесконечно долго двигаться в обе сторон, а также читать с ленту и записывать на нее.

В основном машины Тьюринга бывают двух видов:

По словам Валерия, МТ второго типа намного важнее, сложнее и интереснее первого для Computer Science.

Вводные данные машины, например, число, для которого нужно проверить, является ли оно простым, стоят перед запуском машины в выбранной кодировке на ленте, справа от указателя. Например, вот так бы выглядело число 9 (=1001 в двоичной системе) в качестве вводных данных:

Программа машины

Примечание: понятия состояние и переход между состояниями известны из модели конечных автоматов , потому что, по словам автора, МТ — это их модификации, которые могут работать с внешним хранилищем информации (лентой машины Тьюринга), поэтому программу МТ удобнее всего представлять конечным автоматом, который перемещается между состояниями, пишет на ленту, читает с нее и двигает указатель.

Пример: возьмем программу, которая отзеркаливает последовательность 0 и 1, стоящую на ленте, то есть делает String.reverse . Например, 01011 будет трансформировано в 11010.

Примечание: программы ТМ зачастую большие и сложные, делают кучу странной мишуры, постоянно ездят из конца слова в другой конец. Это вытекает из максимальной простоты инструментов ТМ. Программа машины Тьюринга может выполнить любую алгоритмически решаемую задачу, но на это будет затрачено огромное количество времени.

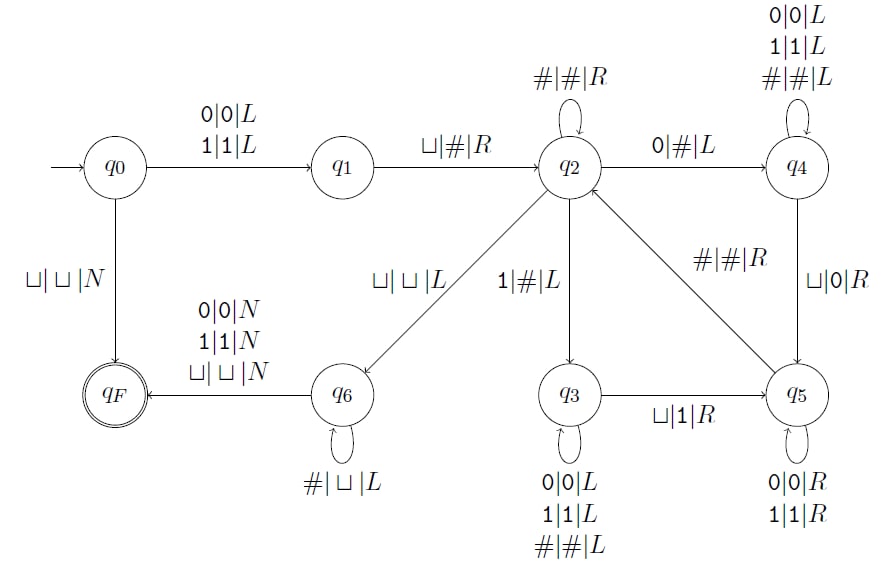
Ниже показано, как будет выглядеть программа МТ, которая будет переворачивать строку. Автор предпочел не разбирать ее подробно, потому что даже такая простая задача может занять ни один час.

Принцип работы программы:

Ниже приведен пример работы этой программы для слова 10, состоящего из двух букв:

Читайте также: