Как сделать свой фрактал python

Обновлено: 03.07.2024

В этой статье приведены примеры расчета и построения графической интерпретации некоторых алгебраических и геометрических фракталов.

Фракталы можно разделить на несколько видов:

Геометрические фракталы – строятся на основе исходной фигуры (линии, многоугольника или многогранника) путем ее дробления и выполнения различных преобразований полученных фрагментов.
Алгебраические фракталы – строятся на основе алгебраических формул.
Стохастические фракталы – получаются, если в итерационном процессе случайным образом изменять какие-либо параметры.

Фракталы нашли применение в физике (моделирование сложных процессов и материалов), биологии (моделирование популяций, описание сложных ветвящихся структур), технике (фрактальные антенны), экономике. Существуют алгоритмы сжатия изображений с помощью фракталов. В компьютерной графике фракталы используются для построения изображений природных объектов – растений, ландшафтов, поверхности морей и т. д.

Некоторые примеры алгебраических и геометрических фракталов

Фрактал Мандельброта

Рассмотрим последовательность комплексных чисел:

\[z_ = z_k^2 + c, k = 0, 1, 2, \dots, z_0 = c\]

Множество точек c, для которого эта последовательность не расходится, называется множеством Мандельброта. Для построения его графической интерпретации нужно определить исходные данные:

прямоугольное окно C с разрешением $m \times n$ точек;
значение $r_ = 2$ – минимальный радиус расходимости множества Мандельброта
максимальное число итераций $k_\max$

Если точка $z_k$ вышла за пределы круга радиуса $r_\min$ при $k \lt k_\max$, то процесс вычисления останавливается.

Построение: для каждой точки $c_ \in C (i = \overline, j = \overline, c_x \in [-2; 1], c_y \in [-2; 1,5])$ запустим итерационный процесс:

\[x_ = x_k^2 - y_k^2 + c_x, x_0 = c_x\] \[y_ = 2 x_k y_k + c_y, y_0 = c_y\]

где $k = 0, 1, 2, \dots, k_\max$ и $\sqrt \leqslant r_\min$.

Составим матрицу M , элементы которой $m_ \in [1; k_\max]$ равны номерам итераций, на которых процесс был остановлен. Далее матрицу можно вывести на экран как растровое изображение, предварительно сопоставив каждому числу из интервала $[1, k_\max]$ некоторый цвет.

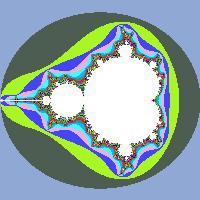
Если представить множество в общем виде:

то, изменяя значение N, можно получать симметричные фрактальные множества. Например, для $N = 4$ и $N = 7$:

Фрактал Жюлиа

Рассмотрим ту же последовательность комплексных чисел, что и для множества Мандельброта:

\[z_ = z_k^2 + c, k = 0, 1, 2, \dots\]

Исходные данные, этапы построения и условия остановки – те же, что и для фрактала Мандельброта, за исключением:

значение c фиксируется: $c = 0,36 + 0,36i$
начальное значение $z_0$ перебирается дискретно в области $C \in [-1;1] + [-1;1]i$

Рассматривая множество в общем виде: $z_ = z_k^N + c$ и изменяя N и с, можно получать разнообразные фрактальные множества:

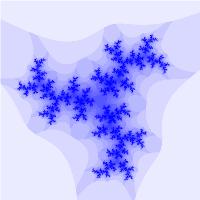
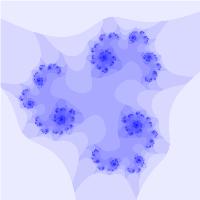
Бассейны Ньютона

Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости.

Общая формула метода Ньютона имеет вид:

При выборе различных $z_0$ процесс будет сходиться к различным корням (областям притяжения). Границы этих областей имеют фрактальную структуру.

Подставив $p(z)$ в формулу метода, получим итерационную формулу для построения фрактала:

Итерационный процесс останавливается при:

\[\left| z_^3 \right| \leqslant r_\min\]

Для построения графической интерпретации также как и для фрактала Мандельброта, используется матрица, элементы которой равны номеру итерации, на которой остановился процесс.

Если записать формулу в общем виде:

\[p(z) = z^N - 1\] \[\left| z_^N - 1 \right| \leqslant r_\min\]

то можно получить изображения фракталов более сложной формы:

L-системы

В 1968 году венгерский биолог Аристид Линденмайер предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена для моделирования сложных ветвящихся структур (разнообразных растений). Эта модель получила название Lindenmayer System (Система Линденмайера или L-система).

Рекурсивная природа L-систем позволяет строить с их помощью геометрические фрактальные изображения.

L-система определяется как $G = (V, \omega, P)$ , где

V - алфавит – множество символов, содержащее элементы, которые могут быть замещены (переменные).
ω – строка символов из множества V, определяющая начальное состояние системы (аксиома).
P – набор правил, определяющий, как переменные могут быть замещены другими переменными и константами.

Правила применяются итеративно, начиная с аксиомы. За одну итерацию применяются одновременно все правила.

Например, L-система имеет вид:

Правила: $(A \rightarrow AB) (B \rightarrow BA)$

После нескольких применений правил из аксиомы получаются строки:

Пример некоторых фракталов, построенных с помощью L-систем - кривая дракона и растение:

Лист папоротника

Существует несколько способов построения этого фрактала.

1) Построение с помощью системы итерируемых функций (IFS)

Производится 20 итераций функции $f(x, y)$. Каждое новое значение получается из предыдущего в зависимости от случайного числа, т. е. вычисляется с использованием таблицы распределения:

Вероятность	$$x'$$	$$y'$$
0,01	$$0$$	$$0,16y$$
0,85	$$0,85x + 0,04y$$	$$-0,04x + 0,85y + 1,6$$
0,07	$$0,20x - 0,26y$$	$$0,23x + 0,22y + 1,6$$
0,07	$$-0,15x + 0,28y$$	$$0,26x + 0,24y + 0,44$$

После выполнения всех итераций точка рисуется на экране.

Начальные значения x и y могут быть константами (желательно не большими, чем 1) или их можно выбирать случайным образом на отрезке $[0;1]$.

2) Рекурсивное построение

Для построения используется процедура (псевдокод):

$R(\phi) = \begin \cos(\phi) && \sin(\phi) \\ -\sin(\phi) && \cos(\phi) \end$ - матрица поворота на угол φ.

$p_0 = [x_0; y_0]$ - координаты начальной точки
h – высота листа
ψ – угол отклонения листа от вертикали
side – направление изгиба ветви
δ – минимальная длина ветви ветвящегося отрезка
rec – максимальная глубина рекурсии

Рекомендуемые значения углов и коэффициентов: $\phi_0 = 14,9^, \phi_1 = 37,7^, \phi_2 = 36,8^, \phi_3 = 17,6^, k_1 = 0,0483, k_2 = 0,162, m_1 = 0,371, m_2 = 0,336, m_3 = 0,849$.

Для получения более реалистичного изображения можно использовать метод управляемой случайности. Метод заключается в том, что в процесс сознательно вносятся помехи. В алгоритме построения ветви папоротника можно внести изменения в углы ветвления φ1, φ2, φ3.

Например, если ввести случайные воздействия на углы помех, равномерно распределенных на интервале $(-10^; 10^)$, можно получить изображения:

Литература:

Программы

Здесь приведены ссылки на программы, с помощью которых были созданы иллюстрации для этой статьи.

Имеется два числа, допустим массив в три ячейки и 1, 2 по его бокам, а в центре должен быть сам список. По сути, массив, который уходит в бесконечность. Пример: [1, [1, [1. 2], 2], 2]. Как можно это реализовать?

при чём здесь фрактал? (потому что некоторые фракталы самоподобные?) Вы хотите список, который сам на себя ссылается? Вы рекурсивную структуру хотите создать? Self-referencing lists in python

2 ответа 2

Всё ещё ищете ответ? Посмотрите другие вопросы с метками python алгоритм или задайте свой вопрос.

2 ответа

Вы также можете использовать тот факт, что обе стороны фигуры симметричны:

Не самая быстрая реализация, но она компактна и заставляет вас гадать, куда она пойдет дальше:

Сначала мы подходим к верхней правой ноге H, поворачиваемся внутрь и возвращаемся. Как только мы закончим рекурсию, мы продолжаем поворачиваться в том же направлении, чтобы двигаться вниз по руке. Вместо того, чтобы двигаться полностью вниз по руке (эффективная вещь), мы возвращаемся к нашей исходной точке, но теперь мы сталкиваемся с противоположным путем, поэтому мы просто повторяем все, что мы делали до сих пор, чтобы нарисовать нижний левый угол H. ,

Как только это закончится, мы снова находимся в центре, указывая снова в исходном направлении, поэтому мы повторяем весь процесс снова, но превращаем все наши права в левые, и наоборот, отрицая угол. Это рисует нашу нижнюю левую ногу, а затем заканчивается верхней правой ногой.

Читайте также: