Как сделать сечение в кубе

Обновлено: 07.07.2024

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Замечание

Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.

Важные определения

1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.

3. Прямая и плоскость параллельны, если они не имеют общих точек.

4. Две плоскости параллельны, если они не имеют общих точек.

5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен \(90^\circ\) .

6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

7. Две плоскости называются перпендикулярными, если угол между ними равен \(90^\circ\) .

Важные аксиомы

1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Важные теоремы

1. Если прямая \(a\) , не лежащая в плоскости \(\pi\) , параллельна некоторой прямой \(p\) , лежащей в плоскости \(\pi\) , то она параллельна данной плоскости.

2. Пусть прямая \(p\) параллельна плоскости \(\mu\) . Если плоскость \(\pi\) проходит через прямую \(p\) и пересекает плоскость \(\mu\) , то линия пересечения плоскостей \(\pi\) и \(\mu\) — прямая \(m\) — параллельна прямой \(p\) .

3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

4. Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\) , то линии пересечения плоскостей также параллельны:

\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]

5. Пусть прямая \(l\) лежит в плоскости \(\lambda\) . Если прямая \(s\) пересекает плоскость \(\lambda\) в точке \(S\) , не лежащей на прямой \(l\) , то прямые \(l\) и \(s\) скрещиваются.

6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.

7. Теорема о трех перпендикулярах.

Пусть \(AH\) – перпендикуляр к плоскости \(\beta\) . Пусть \(AB, BH\) – наклонная и ее проекция на плоскость \(\beta\) . Тогда прямая \(x\) в плоскости \(\beta\) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.

8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.

Замечание

Еще один важный факт, часто использующийся для построения сечений:

для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.

Для этого из двух произвольных точек \(A\) и \(B\) прямой \(a\) проведем перпендикуляры на плоскость \(\mu\) – \(AA'\) и \(BB'\) (точки \(A', B'\) называются проекциями точек \(A,B\) на плоскость). Тогда прямая \(A'B'\) – проекция прямой \(a\) на плоскость \(\mu\) . Точка \(M=a\cap A'B'\) и есть точка пересечения прямой \(a\) и плоскости \(\mu\) .

Причем заметим, что все точки \(A, B, A', B', M\) лежат в одной плоскости.

Пример 1.

Дан куб \(ABCDA'B'C'D'\) . \(A'P=\dfrac 14AA', \ KC=\dfrac15 CC'\) . Найдите точку пересечения прямой \(PK\) и плоскости \(ABC\) .

Решение

1) Т.к. ребра куба \(AA', CC'\) перпендикулярны \((ABC)\) , то точки \(A\) и \(C\) — проекции точек \(P\) и \(K\) . Тогда прямая \(AC\) – проекция прямой \(PK\) на плоскость \(ABC\) . Продлим отрезки \(PK\) и \(AC\) за точки \(K\) и \(C\) соответственно и получим точку пересечения прямых – точку \(E\) .

2) Найдем отношение \(AC:EC\) . \(\triangle PAE\sim \triangle KCE\) по двум углам ( \(\angle A=\angle C=90^\circ, \angle E\) – общий), значит, \[\dfrac=\dfrac\]

Если обозначить ребро куба за \(a\) , то \(PA=\dfrac34a, \ KC=\dfrac15a, \ AC=a\sqrt2\) . Тогда:

Пример 2.

Дана правильная треугольная пирамида \(DABC\) с основанием \(ABC\) , высота которой равна стороне основания. Пусть точка \(M\) делит боковое ребро пирамиды в отношении \(1:4\) , считая от вершины пирамиды, а \(N\) – высоту пирамиды в отношении \(1:2\) , считая от вершины пирамиды. Найдите точку пересечения прямой \(MN\) с плоскостью \(ABC\) .

Решение

1) Пусть \(DM:MA=1:4, \ DN:NO=1:2\) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку \(O\) пересечения медиан основания. Найдем проекцию прямой \(MN\) на плоскость \(ABC\) . Т.к. \(DO\perp (ABC)\) , то и \(NO\perp (ABC)\) . Значит, \(O\) – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр \(MQ\) из точки \(M\) на плоскость \(ABC\) . Точка \(Q\) будет лежать на медиане \(AK\) .
Действительно, т.к. \(MQ\) и \(NO\) перпендикулярны \((ABC)\) , то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки \(M, N, O\) лежат в одной плоскости \(ADK\) , то и точка \(Q\) будет лежать в этой плоскости. Но еще (по построению) точка \(Q\) должна лежать в плоскости \(ABC\) , следовательно, она лежит на линии пересечения этих плоскостей, а это – \(AK\) .

Значит, прямая \(AK\) и есть проекция прямой \(MN\) на плоскость \(ABC\) . \(L\) – точка пересечения этих прямых.

2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки \(L\) (например, на нашем чертеже точка \(L\) лежит вне отрезка \(OK\) , хотя она могла бы лежать и внутри него; а как правильно?).

Т.к. по условию сторона основания равна высоте пирамиды, то обозначим \(AB=DO=a\) . Тогда медиана \(AK=\dfrac2a\) . Значит, \(OK=\dfrac13AK=\dfrac 1a\) . Найдем длину отрезка \(OL\) (тогда мы сможем понять, внутри или вне отрезка \(OK\) находится точка \(L\) : если \(OL>OK\) – то вне, иначе – внутри).

а) \(\triangle AMQ\sim \triangle ADO\) по двум углам ( \(\angle Q=\angle O=90^\circ, \ \angle A\) – общий). Значит,

\[\dfrac=\dfrac=\dfrac=\dfrac 45 \Rightarrow MQ=\dfrac 45a, \ AQ=\dfrac 45\cdot \dfrac 1a\]

Значит, \(QK=\dfrac2a-\dfrac 45\cdot \dfrac 1a=\dfrac7a\) .

б) Обозначим \(KL=x\) .
\(\triangle LMQ\sim \triangle LNO\) по двум углам ( \(\angle Q=\angle O=90^\circ, \ \angle L\) – общий). Значит,

Следовательно, \(OL>OK\) , значит, точка \(L\) действительно лежит вне отрезка \(AK\) .

Замечание

Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что \(x\) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки \(L\) (то есть, что она находится внутри отрезка \(AK\) ).

Пример 3

Дана правильная четырехугольная пирамида \(SABCD\) . Найдите сечение пирамиды плоскостью \(\alpha\) , проходящей через точку \(C\) и середину ребра \(SA\) и параллельной прямой \(BD\) .

Решение

1) Обозначим середину ребра \(SA\) за \(M\) . Т.к. пирамида правильная, то высота \(SH\) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость \(SAC\) . Отрезки \(CM\) и \(SH\) лежат в этой плоскости, пусть они пересекаются в точке \(O\) .

Для того, чтобы плоскость \(\alpha\) была параллельна прямой \(BD\) , она должна содержать некоторую прямую, параллельную \(BD\) . Точка \(O\) находится вместе с прямой \(BD\) в одной плоскости – в плоскости \(BSD\) . Проведем в этой плоскости через точку \(O\) прямую \(KP\parallel BD\) ( \(K\in SB, P\in SD\) ). Тогда, соединив точки \(C, P, M, K\) , получим сечение пирамиды плоскостью \(\alpha\) .

2) Найдем отношение, в котором делят точки \(K\) и \(P\) ребра \(SB\) и \(SD\) . Таким образом мы полностью определим построенное сечение.

Заметим, что так как \(KP\parallel BD\) , то по теореме Фалеса \(\dfrac=\dfrac\) . Но \(SB=SD\) , значит и \(SK=SP\) . Таким образом, можно найти только \(SP:PD\) .

Рассмотрим \(\triangle ASC\) . \(CM, SH\) – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении \(2:1\) , считая от вершины, то есть \(SO:OH=2:1\) .

Теперь по теореме Фалеса из \(\triangle BSD\) : \(\dfrac=\dfrac=\dfrac21\) .

3) Заметим, что по теореме о трех перпендикулярах \(CO\perp BD\) как наклонная ( \(OH\) – перпендикуляр на плоскость \(ABC\) , \(CH\perp BD\) – проекция). Значит, \(CO\perp KP\) . Таким образом, сечением является четырехугольник \(CPMK\) , диагонали которого взаимно перпендикулярны.

Пример 4

Дана прямоугольная пирамида \(DABC\) с ребром \(DB\) , перпендикулярным плоскости \(ABC\) . В основании лежит прямоугольный треугольник с \(\angle B=90^\circ\) , причем \(AB=DB=CB\) . Проведите через прямую \(AB\) плоскость, перпендикулярную грани \(DAC\) , и найдите сечение пирамиды этой плоскостью.

Решение

1) Плоскость \(\alpha\) будет перпендикулярна грани \(DAC\) , если она будет содержать прямую, перпендикулярную \(DAC\) . Проведем из точки \(B\) перпендикуляр на плоскость \(DAC\) — \(BH\) , \(H\in DAC\) .

Проведем вспомогательные \(BK\) – медиану в \(\triangle ABC\) и \(DK\) – медиану в \(\triangle DAC\) .
Т.к. \(AB=BC\) , то \(\triangle ABC\) – равнобедренный, значит, \(BK\) – высота, то есть \(BK\perp AC\) .
Т.к. \(AB=DB=CB\) и \(\angle ABD=\angle CBD=90^\circ\) , то \(\triangle ABD=\triangle CBD\) , следовательно, \(AD=CD\) , следовательно, \(\triangle DAC\) – тоже равнобедренный и \(DK\perp AC\) .

Применим теорему о трех перпендикулярах: \(BH\) – перпендикуляр на \(DAC\) ; наклонная \(BK\perp AC\) , значит и проекция \(HK\perp AC\) . Но мы уже определили, что \(DK\perp AC\) . Таким образом, точка \(H\) лежит на отрезке \(DK\) .

Соединив точки \(A\) и \(H\) , получим отрезок \(AN\) , по которому плоскость \(\alpha\) пересекается с гранью \(DAC\) . Тогда \(\triangle ABN\) – искомое сечение пирамиды плоскостью \(\alpha\) .

2) Определим точное положение точки \(N\) на ребре \(DC\) .

Обозначим \(AB=CB=DB=x\) . Тогда \(BK\) , как медиана, опущенная из вершины прямого угла в \(\triangle ABC\) , равна \(\frac12 AC\) , следовательно, \(BK=\frac12 \cdot \sqrt2 x\) .

Рассмотрим \(\triangle BKD\) . Найдем отношение \(DH:HK\) .

Заметим, что т.к. \(BH\perp (DAC)\) , то \(BH\) перпендикулярно любой прямой из этой плоскости, значит, \(BH\) – высота в \(\triangle DBK\) . Тогда \(\triangle DBH\sim \triangle DBK\) , следовательно

\[\dfrac=\dfrac \Rightarrow DH=\dfrac3x \Rightarrow HK=\dfrac6x \Rightarrow DH:HK=2:1\]

Рассмотрим теперь \(\triangle ADC\) . Медианы треугольника точной пересечения делятся в отношении \(2:1\) , считая от вершины. Значит, \(H\) – точка пересечения медиан в \(\triangle ADC\) (т.к. \(DK\) – медиана). То есть \(AN\) – тоже медиана, значит, \(DN=NC\) .

Здесь рассмотрено подробное решение двух наиболее сложных, на мой взгляд, задач из представленных в группе Задачи на построение сечений многогранников на этом сайте. Если Вы еще не выполняли подобных заданий, вернитесь на указанную страницу и попробуйте поработать самостоятельно.

Задача 6.

Итак, задан куб c диагональю и точкой на ней.

Замечание: куб на чертеже может быть повёрнут к нам любой гранью, но трудно предугадать, какой удобнее для построения. Поэтому, если совсем не получается решение какой-либо задачи по стереометрии, то я рекомендую начинать заново, перерисовав исходный чертёж. А зачастую бывает достаточно просто переставить символы, обозначающие вершины основания многоугольника (естественно, не произвольно, а согласовав между собой и с условием задачи).

Для начала вспомним признак перпендикулярности прямой и плоскости.

Теорема. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения, то она перпендикулярна плоскости.

Таким образом, для построения плоскости, проходящей через заданную точку перпендикулярно заданной прямой, нам нужно найти еще две прямые, которые проходят через эту точку, и каждая из них перпендикулярна заданной прямой. Назовём их пока прямая 1 и прямая 2. Прямая 1 должна пересекаться с B₁D в точке K, следовательно через эти две прямые может быть проведена плоскость.

Аксиома. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Аналогично прямая 2 должна пересекаться с B₁D в точке K, следовательно через эти две прямые тоже может быть проведена плоскость. Согласно приведенной аксиоме, если прямые 1 и 2 не совпадают, то и плоскости, проведенные через каждую из них и заданную прямую не совпадают.

Поэтому для реализации нашей цели нужно найти две различные плоскости, содержащие прямую B₁D, и построить в них нужные перпендикуляры. В качестве таковых в кубе можно взять, например, плоскости B₁BDD₁ и B₁ADC₁

Если не получается сразу понять, какие плоскости в кубе проходят через его диагональ, можете попробовать формальный подход:
- между символами, обозначающими две вершины куба B₁ и D, вставить третий символ – любую другую вершину куба.
B₁AD, B₁A₁D, B₁BD, B₁CD, B₁C₁D, B₁D₁D – это плоскости, т.к. мы брали три точки, не лежащие на одной прямой, и эти плоскости содержат нужную прямую, т.к. две точки этой прямой точно принадлежат плоскости. (См. соответствущие теоремы о плоскостях.) Другое дело, что соединив по три точки между собой на чертеже, вы сможете увидеть только часть выбранной плоскости. Чтобы продолжить её до пересечения с гранями куба и построить полное сечение, нужно воспользоваться теоремой о пересечении двух параллельных плоскостей (граней куба) третьей плоскостью и достроить треугольники до параллелограммов. При этом обнаружится, что некоторые плоскости совпадают:
B₁AD и B₁C₁D образуют сечение B₁ADC₁
B₁A₁D и B₁CD образуют сечение B₁A₁DC
B₁BD и B₁D₁D образуют сечение B₁BDD₁
Аналогичный формальный подход можно применять и к другим многогранникам, только не забывайте о том, что он должен контролироваться аксиомами стереометрии и теоремами о плоскостях.

Построим сечение B₁BDD₁. Две противоположные стороны этого четырёхугольника являются рёбрами куба, а две другие - диагоналями его граней. По свойствам куба можем сделать вывод, что B₁BDD₁ – прямоугольник длина которого в √2 _ раз больше ширины. Делим диагональ на 4 части и ставим точку К, удовлетворяющую условию B₁K : B₁D = 1 : 4. Проводим через эту точку перпендикуляр к B₁D. Отрезок MN лежит на одной из искомых прямых.
При необходимости легко уточнить положение точек M и N на поверхности куба. Если задана длина ребра (или можно обозначить её, например, символом a), то длины отрезков B₁M и B₁N легко вычисляются из подобия прямоугольных треугольников, которое хорошо просматривается на плоском чертеже.

Получили четыре точки, принадлежащие искомой плоскости сечения и поверхности куба. Соединяем прямой линией точки M и F на грани BСС₁B₁. Соединяем точки F и N на грани A₁B₁С₁D₁ и продолжаем прямую до пересечения с ребром A₁B₁ в точке R. Соединяем точки R и E на грани A₁B₁BA и продолжаем прямую до пересечения с ребром B₁B в точке. M ? Но где гарантия, что именно в точке M, а не выше или ниже по ребру?

Если были проведены вычисления отрезков B₁F = B₁M и B₁N = B₁E в процессе анализа плоских прямоугольников, то ответ становится очевидным: так как прямоугольные треугольники B₁RF, B₁RM и B₁FM равнобедренные и равные.
Если же при построении положение точек M и F не вычислялось, а контролировался только факт их положения на рёбрах куба, то придётся произвести ряд вычислений на этапе доказательства верности построения.

Замечание I.
Возможен альтернативный подход к этой задаче. Так как куб является правильным многогранником и имеет центр симметрии, расположенный в точке пересечения диагоналей, а значит на линии B₁D, с которой мы работаем, то можно предположить, что сечение также будет симметричным и будет иметь форму равностороннего треугольника. Поэтому после анализа (жёлтого) прямоугольника на первом чертеже и получения точки М, можно сразу отложить от вершины B₁ на рёбрах куба равные отрезки B₁R = B₁F = B₁M, а затем доказать, что плоскость RMF перпендикулярна прямой B₁D. Для этого лучше всего воспользоваться теоремой о трёх перпендикулярах.

Теорема. Прямая, проведенная на плоскости через основание наклонной перпендикулярно её проекции, перпендикулярна и самой наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Замечание II.
Вид сечения сильно зависит от положения точки K на диагонали куба. Попробуйте сместить точку K ближе к середине отрезка B₁D и построить MN ⊥ B₁D в прямоугольнике B₁BDD₁. На каких гранях и рёбрах куба теперь окажутся точки искомого сечения?

Ниже вы можете посмотреть маленькое видео о том, как изменяется сечение куба плоскостью, перпендикулярной его диагонали, в зависимости от положения их точки пересечения.

Задача 16.

Через точки P, R и Q, заданные соответственно на ребрах СВ, CD и СС₁ призмы ABCDA₁B₁C₁D₁ проведена плоскость. Постройте сечение призмы плоскостью, параллельной плоскости PQR и проходящей через точку А₂ на ребре АА₁.

Этот чертёж полностью соответствует условию задачи. Однако ваши чертежи могут несколько отличаться от него по внешнему виду и восприятию, так как в этой задаче основанием призмы может быть произвольный четырёхугольник, призма может быть развёрнута "к зрителю" любой гранью, точки на рёбрах призмы могут быть расположены на разных расстояних от её вершин. Это не имеет значения для решения задачи, если при построении сечения вы будете действовать на основе доказанных теорем о прямых и плоскостях в пространстве. При этом верными ответами могут оказаться сечения разной формы.

При решении задачи предполагаем, что все операции на плоскости, в частности, построение параллельных и перпендикулярных прямых, нам известны из планиметрии и в подробном описании не нуждаются.

Решение.

Чтобы построить плоскость, параллельную заданной плоскости, нужно вспомнить признак параллельности двух плоскостей.

Теорема. Две плоскости параллельны, если одна из них параллельна двум пересекающимся прямым, лежащим в другой плоскости.

Таким образом, нам нужно найти две пересекающиеся прямые, каждой из которых параллельна плоскость PQR. Или, что то же самое, каждая из которых параллельна плоскости PQR. В каком случае прямая параллельна плоскости? На этот вопрос отвечает признак параллельности прямой и плоскости.

Теорема. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

Кроме того, нам нужно, чтобы плоскость сечения проходила через заданную точку А₂. Значит, хорошо бы сразу найти две такие пересекающиеся прямые, параллельные каким-либо прямым в плоскости PQR, чтобы хотя бы одна из них содержала точку А₂. В этом и будет состоять первый этап решения задачи.

Через точки R и Р проводим РN || CC₁ и RM || CC₁ . Соединяем точки M и N прямой линией. По свойствам призмы получим MN || RР и MN = RР .

Терерь рассмотрим диагональное сечение призмы, проведенное через параллельные прямые AA₁ и СС₁. Плоскость AA₁C₁C содержит заданные точкии A₂ и Q и пересекает заданную плоскость PQR по линии QE. (Буквой Е обозначена общая точка линии пересечения плоскостей и прямой RP.) В этой плоскости (голубой на чертеже) через точку А₂ проводим прямую, параллельную QE до пересечения с верхним основанием призмы в точке F. А₂F || QE по построению.

На верхней грани призмы через точку F проводим прямую, параллельную линии MN, которая в нашем случае пересекает рёбра призмы A₁D₁ и B₁C₁ в точках H и G соответственно. HG || MN .
В зависимости от положения точки А₂ на ребре АА₁ положение точек H и G на рёбрах призмы может изменяться. Например, если бы точка А₂ располагалась ближе к вершине А₁, то точка G могла бы оказаться на ребре А₁В₁, а если бы она находилась близко к вершине А, то точка Н могла бы оказаться на ребре D₁С₁. От этого зависит окончательная форма искомого сечения призмы. Т.е. поскольку в условии задачи положение точек на рёбрах не фиксировано, то ваши ответы могут отличаться от приведенного мной не только формой на чертеже, но и количеством сторон получившегося многоугольника.

Обе прямые HG и RР параллельны прямой MN по построению, следовательно HG || RР . Для прямых в плоскости это вам уже известно давно. Для прямых в пространстве это тоже доказано.

Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Таким образом, прямые А₂F и HG и есть те самые прямые, которые мы искали. А₂F параллельна QE, следовательно параллельна плоскости PQR. HG параллельна RР, следовательно параллельна плоскости PQR. А₂F и HG пересекаются в точке F. Эти прямые определят секущую плоскость, параллельную заданной PQR.

Нам остаётся найти линии пересечения этой плоскости с гранями призмы, т.е. построить собственно само сечение.

Продолжим прямую HG до пересечения с ребром A₁B₁ в точке L. Точка L принадлежит верхней и фронтальной (на нашем чертеже) граням призмы, поскольку она принадлежит их общему ребру. Кроме того, точка L принадлежит плоскости сечения, поскольку находится на прямой HG. Следовательно, эта точка должна принадлежать и линии пересечения фронтальной грани с плоскостью сечения. Соединяем точку L с точкой А₂. Эта прямая будет принадлежать плоскости грани АА₁В₁В на основании следующей теоремы.

Теорема. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

Пользуясь этим же утверждением, соединяем и остальные две пары точек, принадлежащих одной грани призмы.

То, что оно удовлетворяет условию проходить через точку А₂ очевидно по построению. То, что плоскость A₂HGK параллельна плоскости RQP мы доказали, ссылаясь на соответствующие положения теории на каждом шаге построения.

Замечание.
Конечно, во время экзамена вы не будете делать несколько чертежей и так подробно описывать построение. Итоговый чертёж будет выглядеть примерно так.
Однако, не забывайте, что основное требование к заданиям второй части ЕГЭ профильного уровня это обоснованность решения. Поэтому, если вы просто выполнили все построения и представили на проверку итоговый чертёж, то к нему необходимо написать доказательство, которое содержит ссылки на теорию. При этом не обязательно цитировать теоремы полностью, можно упомянуть их названия.

Внимание: Если вы нашли ошибку или опечатку, пожалуйста, сообщите о ней на email.

Понравились материалы сайта?
Узнайте, как поддержать сайт и помочь его развитию.

Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Общеобразовательная школа І-ІІІ ступеней №2

отдела образования администрации города Кировское

«Сечение куба плоскостью

Подготовила учитель математики

2015 г.

Задачи на построение сечений многогранников занимают значительное место как школьном курсе геометрии для старших классов, так и на экзаменах разного уровня. Решение этого вида задач способствует усвоению аксиом стереометрии, систематизации знаний и умений, развитию пространственного представления и конструктивных навыков. Общеизвестны трудности, возникающие при решении задач на построение сечений.

Основными действиями, составляющими метод построения сечений, являются нахождение точки пересечения прямой с плоскостью, построение линий пересечения двух плоскостей, построение прямой параллельной плоскости, построение прямой перпендикулярной плоскости.

Проиллюстрирую построение сечения на одной задаче из школьного курса математики:

№1. Постройте хотя бы два сечения куба ABCDA ₁ B ₁ C ₁ D ₁ плоскостью АМ₁С, если точка М₁ движется по отрезку ВВ₁ от В до В₁. Найдите границы измерения высоты сечения, проведённой из точки М₁.

Решение: Построим два требуемых сечения, взяв точку М₁ ближе к точке В, а точку М₂ближе к В₁. Оба сечения показаны на рисунке .В начале движения когда точка М₁только отошла от точки В₁, сечение представляет собой треугольник с основанием АС и высотой М₁О, которая чуть больше отрезка ВО, т.е. Если точка М₁ займёт положение М₂расположенной очень близко к точке В₁, то АМ₂С почти совпадёт с АВ₁С, а его высота М₁О – с отрезком В₁О, длина которого равна (ОВ₁==).

Отсюда по соображениям непрерывности делаем вывод:

Особо следует посмотреть, что произойдёт, если точка М₁ займёт положение вершины В.

№2. Построить сечение куба плоскостью, проходящей через три точки А₁, E и L , лежащие на рёбрах куба.

Плоскости граней A ₁ ADD ₁ и DD ₁ C ₁ C пересекаются по прямой DD ₁, а плоскости граней A ₁ B ₁ C ₁ D ₁ u DD ₁ C ₁ C – по прямой D ₁ C ₁. Соединив точки А и Е , получим прямую пересечения секущей плоскости с плоскостью грани AA ₁ D ₁ D , а продолжив её, найдём точку N , принадлежащую трём плоскостям: плоскости сечения и плоскостям граней AA ₁ D ₁ D u DD ₁ C ₁ C .

Аналогично найдём точку М, общую трём плоскостям: плоскости сечения и плоскостям граней A ₁ B ₁ C ₁ D ₁ u DD ₁ C ₁ C . Таким образом, точки N u M принадлежат секущей плоскости и плоскости DD ₁ C ₁ C ; прямая MN – линия пересечения плоскости сечения с плоскостью грани DD ₁ C ₁ C , а F и K – точки пересечения её с рёбрами куба CD u CC ₁. Последовательно соединив прямыми точки A ₁, E , F , K u L , получаем пятиугольник A _! EFKL , который и даст нам искомое сечение.

При построении сечения куба плоскостью Х при произвольном расположении точек в сечении получается: треугольник, трапеция, прямоугольник, пятиугольник или шестиугольник. Естественно возник вопрос, как вид сечения зависит от вида расположения точек задающих это сечение

Я решил провести исследование, цель которого является выяснение.

Построить сечения куба плоскостью, когда заданы три точки принадлежащие рёбрам с одной вершиной.

Взяты три точки A ₁, D , C ₁, которые принадлежат вершине D ₁, а сами являются вершинами куба.

В сечении получился равносторонний треугольник, так как A ₁ C ₁, A ₁ D u DC ₁ – диагонали граней этого куба.

Три точки: A ₁ u C ₁ – вершины куба, а точка F принадлежит ребру куба DD ₁. Точки принадлежат прямым выходящим из вершины D ₁.

В сечении получился равнобедренный треугольник, так как F равноудалена от точек A ₁ u C ₁.

Три точки: A ₁ u C ₁ – вершины куба, а точка F принадлежит прямой ребра куба DD ₁. Точки принадлежат прямым выходящим из одной вершины D ₁.

В сечении получается равнобедренная трапеция, так как F равноудалена от точек A ₁ u C ₁, то есть LA ₁= KC ₁.

Три точки принадлежащие рёбрам с одной вершиной D ₁. Точки F u M принадлежат продолжениям рёбер D ₁ D u D ₁ C соответственно, а точка A ₁ является вершиной куба.

В сечении получился пятиугольник A ₁ KLNG .

Взяты три точки F , M u Q так, что лежат на продолжении рёбер D ₁ D , D ₁ C ₁, и D ₁ A ₁ соответственно.

В сечении получился шестиугольник KLNGJH .

Три точки лежат на рёбрах с одной вершиной D ₁.

В сечении получился произвольный треугольник, но если точки расположить так чтобы D ₁ Q = D ₁ M = D ₁ F , то есть если они были бы равноудалены от вершины D ₁ то в сечении получился бы равносторонний треугольник.

Секущая плоскость задана точками Н, Q и M . В сечении получается параллелограмм, так как KC ││ MP и MK ││ PC по теореме о пересечении двух параллельных плоскостей третьей.

Если точки H , Q и M , задают секущую плоскость, удаленные от D , на расстоянии 2 a , где а – для ребра куба, то в сечении получается правильный треугольник ACB ₁.

Вывод: три задающих сечение точки принадлежат трём рёбрам куба с общей вершиной или являются их продолжением, то в сечении получается: треугольник, пятиугольник, шестиугольник трапеция, параллелограмм.

Построение сечения куба плоскостью, когда заданы три точки, две из которых лежат на смежных рёбрах, а третья точка лежит на ребре не смежном с ними.

Три точки M , K u F , взяты так что M u F принадлежат рёбрам с одной вершиной A ₁, а точка K лежит на ребре не смежным с ними.

В сечении получается прямоугольник, так как А₁М= D ₁ K и по теореме о трёх перпендикулярах можно доказать что MKLF – прямоугольник., а если А₁М D ₁ K , то может получится трапеция или пятиугольник.

Взяты три точки так, что K u L принадлежат рёбрам выходящим из одной вершины A _1, а точка N принадлежит ребру CC ₁, не смежному сними. K , L u N середины рёбер A ₁ A , A ₁ B ₁ u CC ₁ – соответственно.

В сечении получается правильный шестиугольник KLGNHM

Взяты три точки так, что K u L принадлежат рёбрам выходящим из одной вершины A _1, а точка T принадлежит ребру DC .

В сечении получается шестиугольник KLFRTZ .

Три точки взяты так, что K u L принадлежат рёбрам куба с одной вершины A ₁, а точка M ребре DD ₁.

В сечении получается трапеция LKQM .

Три точки K u L которые принадлежат рёбрам с одной вершиной A ₁.и точка R которая лежит на ребре BC .

В сечении получается пятиугольник KLFRT .

Вывод: Если секущая плоскость задана тремя точками, две из которых лежат на смежных рёбрах, а третья на ребре не смежном с ними, то в сечении может получиться прямоугольник, пятиугольник, шестиугольник, трапеция.

В сечении куба параллелограмм и его частные случаи.

Точки T , H , J задающие сечение расположены так, что THAD , HJAD . В сечении получается квадрат HTKJ .

Сечение задано точками C , F , L , причём DF = FD ₁, BL = LB ₁. В сечении получается ромб AFCL .

Сечение задано точками C , G , H . B ₁ H = DG . В сечении параллелограмм A ₁ GCH.

Точки задающие сечение являются вершинами куба A , D , C ₁. В сечении получается прямоугольник

В сечении куба правильные многоугольники

Треугольник АВВ₁ равносторонний, так как его стороны это диагонали граней куба.

Треугольник КМТ равносторонний, так как КВ=МВ=ТВ.

КМТЕ – квадрат, так как сечение задано точками М, К, Е и МК AD , EKAD .

В сечении правильный шестиугольник КМТНЕО, так как точки Н, Е, К задающие сечение являются серединами рёбер СС₁, DC , АА₁ соответственно.

Куб и несколько задач по стереометрии с ЕГЭ.

В пособии “ЕГЭ 2005. Математика. Типовые тестовые задачи” (Корникова Т. А. и др.) Содержит 10 задач (С4) по стереометрии, объединенных общей идеей: дана треугольная призма АВСА ₁ В ₁ С ₁ стороны основания АВ и ВС взаимно перпендикулярны и перпендикулярны ребру ВВ ₁ , АВ=ВС=ВВ ₁ , вершина А является вершиной конуса (или центром одного из оснований цилиндра, или центром сферы), основание конуса (сфера или второе основание цилиндра) проходит через середину одного ребра призмы, длина его известна. Надо найти объем или поверхность конуса (сферы, цилиндра).

Общий пример решения:

Данную призму дополнить до куба. Шестиугольник DEFKLM – сечение куба плоскостью основания конуса , окружность которого проходит через середину А₁В₁, А – вершина конуса, или

DEFKLM – сечение куба плоскостью основания цилиндра, окружность которого проходит через середину А₁В₁, А – центр второго основания цилиндра, или это сечение куба плоскостью большого круга сферы с центром А, сфера которого проходит через середину А₁В₁.

Шестиугольник DEFKLM – сечение куба плоскостью, проходящей через середину рёбер А ₁ В ₁ , ВВ ₁ , ВСЖ при построении получаются точки K , L , M , которые являются серединами соответствующих рёбер. Стороны этого шестиугольника являются гипотенузами треугольников DB ₁ E , EBF , FCK , KQL , LRM , MA ₁ D , катеты которых равны половине ребра куба. Тогда центр этого шестиугольника является центром описанной около него окружности, которая пересекает рёбра куба в точках D , E , F , K , L и М, радиус этой окружности , где А ₁ В ₁ = а .

AO EL, т . к . EAL – равнобедренный: AL = AE .

( ABE u EAL – прямоугольные, AB = AQ = а, BE = LQ = )

EO = OL как середина диагонали Е L шестиугольника DEFKLM , т. е. АО – медиана ,а по свойствам равнобедренного треугольника и высота. Аналогично доказывается АО DK . Так как АО перпендикулярна к двум пересекающимся прямым плоскости шестиугольника, то АО перпендикулярна ко всей плоскости.

Если А – вершина конуса то АО – его высота, если А – центр второго основания цилиндра, то АО- высота цилиндра.

АВС: АС=, P – точки пресечения диагоналей основания куба, АР=, РР ₁ =АА ₁ = а . ОР=РР ₁ = , тогда из прямоугольного РОА АО=. И так АО=.

Здравствуйте, подписчики моего блога!

Многие сталкивались со сложностью в рисовании, когда хотели изобразить сложный по форме объект. Дело в том, что в основе всех сложных структур скрываются простые формы. И куб – одна из таких форм. Сегодня мы подробно разберем, как построить куб.

Перспектива

Куб – это геометрическое тело, состоящее из 6 плоскостей. Знаете, чем отличается куб от квадрата? Куб – это объемная фигура. А при рисовании любых объемных фигур нужно помнить о перспективе.

Из-за законов перспективы стороны куба будут сокращаться, иными словами становиться меньше.

Для начала нужно определить линию горизонта. Это необходимо для того, чтобы правильно построить куб в перспективе.

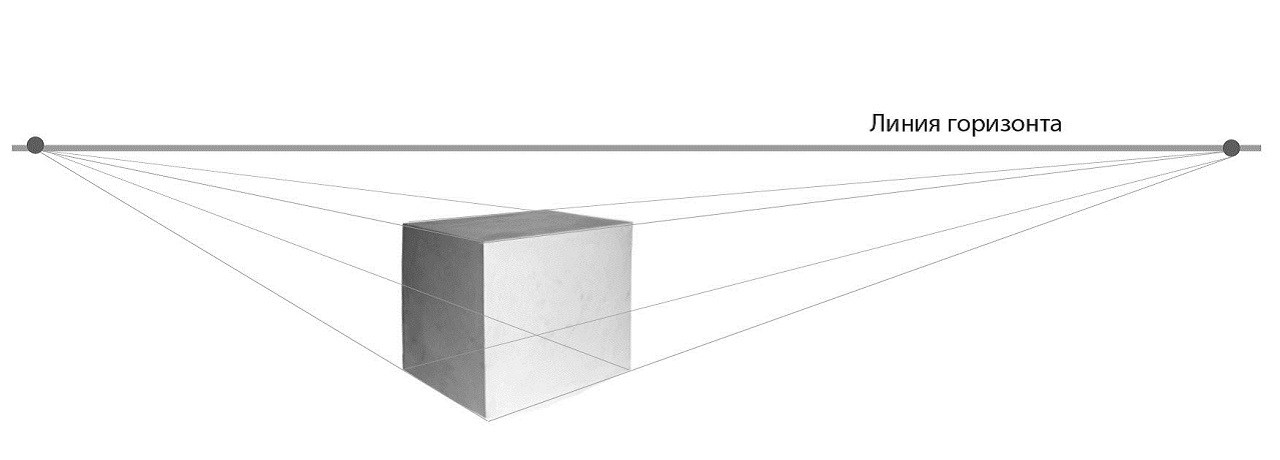
Линия горизонта – это уровень глаз художника. На ней будут располагаться две точки схода. В каждую из этих точек придёт по 4 линии. Наглядно такой рисунок будет выглядеть следующим образом:

Рисуем пошагово

Чтобы было проще воспринять последовательность действий, давайте нарисуем куб пошагово.

Прежде чем заниматься перспективой куба, нужно наметить верные размеры предмета и определить его положение в листе. Куб не должен быть слишком маленьким или, наоборот, слишком большим.

Шаг 1 — Композиция

Композиция – это начало любой работы. От точного нахождения композиции зависит 50% успеха работы.

Следует оставить чуть больше расстояния сверху, чем снизу. Это придаст ощущение весомости.

Начинаем рисунок с самого ближнего к нам ребра куба. Наметьте его так, чтобы оно не совпадало с центром листа. Легкими засечками определяем высоту этого ребра. Так как оно находится ближе всего, его высота будет больше остальных ребер.

Шаг 2 — Сокращение

Плоскости в кубе заметно удаляются в силу перспективного сокращения. Чтобы верно определить это сокращение на листе, необходимо определить углы наклона ребер.

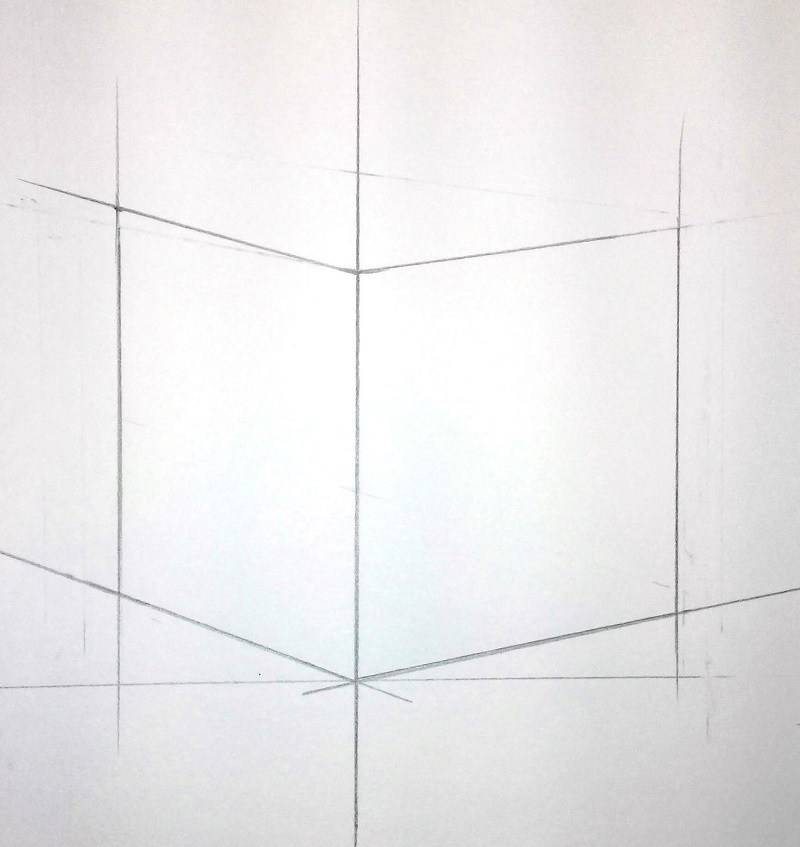
Проводим горизонтальную линию, параллельную листу бумаги, она поможет определить какой угол меньше, а какой больше. Тренируйте свой глаз, переводите взгляд с куба на рисунок, таким образом, перепроверяя себя.

Шаг — 3 — Линейная перспектива

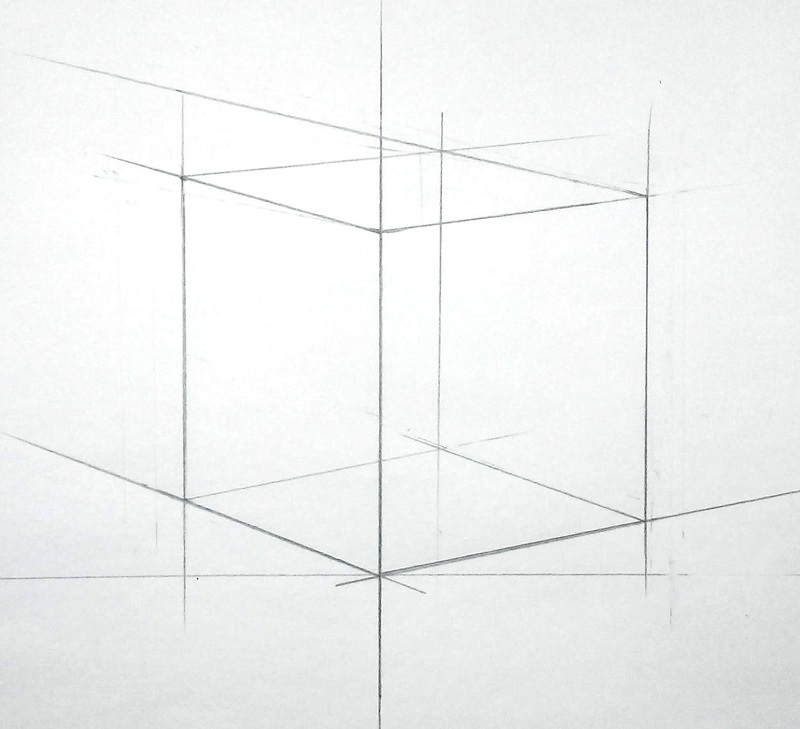
Соединяем горизонтальными линиями пересечения плоскостей в кубе. Помните о том, что они сокращаются, и, если, мы их продлим, то они сойдутся в точке схода.

Невидимые грани мы также должны нарисовать. При правильном построении нужно проверить все сокращения, чтобы не было обратной перспективы.

Шаг 4 — Проверка пропорций

Также можно использовать метод визирования. Вы наверняка замечали, как художники вытягивают руку и измеряют пропорции? Это и есть метод визирования.

Для того, чтобы проверить пропорции, закройте один глаз, возьмите карандаш и на вытянутой руке сопоставьте его кончик с верхом переднего ребра куба. Большой палец передвиньте в то место, где ребро заканчивается.

Высота ребра найдена. Теперь, не переставляя палец, наклоните кисть руки на 90 градусов и уже по горизонтали сопоставьте величину одного ребра с другим. Таким образом вы можете проверять и другие величины.

Итак, линейное построение подошло к концу, а значит, мы переходим к воздушной перспективе или, проще говоря, к штрихованию.

Штрихование

Основная задача рисунка – это передать объем. Внимательно посмотрите на предмет, определите для себя тональность каждой из сторон.

Штриховать следует по форме куба. Внимательно подходите к штриховке, не стоит излишне чернить, все-таки мы рисуем гипсовый куб.

Набирайте тон постепенно, не старайтесь все сделать за один подход. Штрихи можно накладывать и в диагональном направлении.

Используйте карандаши разной мягкости. Для освещённой стороны отлично подойдет твердый карандаш – H, для полутона – HB, а для теневой стороны – B.

Падающая тень

Как построить тень от куба? Чтобы падающая тень была убедительной, давайте рассмотрим основные принципы построения тени на поверхности листа.

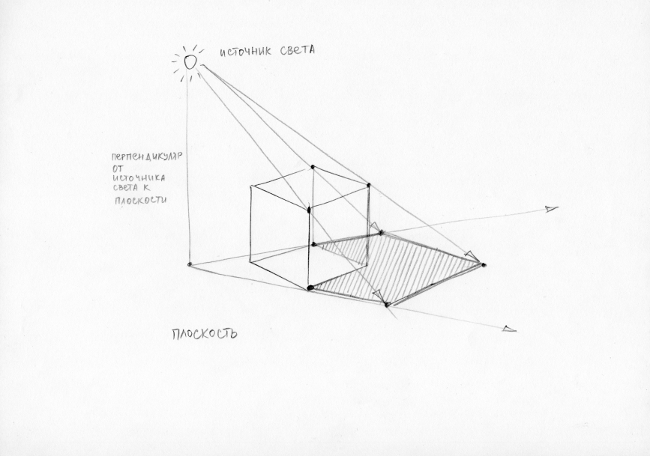
Определяем местонахождения источника света.
Проводим перпендикуляр от источника света к плоскости, где находится наш предмет.
От точки, где перпендикуляр пересекается с плоскостью, проводим линии в касание с углами куба.
Проецируем воображаемые лучи от источника света, которые проходят по вершинам 5 куба. Намечаем точки соприкосновения лучей и плоскости.
Соединяем найденные точки на плоскости и получаем конфигурацию тени.

Падающая тень всегда темнее, чем собственная тень на предмете. Чем ближе она подходит к объекту, тем темнее она становится.

На самом кубе тон становится также активнее на границе двух плоскостей – освещенной и теневой. Теневая сторона, по мере удаления в пространство, высветляется за счет отраженного света от поверхности. Рефлексы помогают передать световоздушное пространство.

Заключение

Мы поговорили о сечении куба плоскостью, о том, как правильно построить куб с натуры в перспективе. Рисование простых геометрических тел весьма полезно для начинающих и тех, кто хочет овладеть академическим рисунком.

Геометрия и расположение плоскостей в пространстве очень хорошо тренирует зрительное восприятие.

Если у вас нет гипсового куба, не беда, смастерите куб из бумаги. Для первых упражнений главное – это понять основные принципы при построении. А затем, можно будет перейти к гипсовым фигурам.

Читайте также: