Как сделать сечение призмы плоскостью

Добавил пользователь Владимир З.
Обновлено: 04.10.2024

Правила построения сечений многогранников:

1) проводим прямые через точки, лежащие в одной плоскости;

2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого

а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

б) параллельные грани плоскость сечения пересекает по параллельным прямым.

Примеры построения сечений:

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Построим сечение, проходящее через точки M, N, L.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

Найдем прямую пересечения плоскости сечения с плоскостью DD₁C₁C:

пересечем прямую ML (принадлежащую сечению) с ребром DD₁, они лежат в одной плоскости AA₁D₁D, получим точку X₂;

пересечем прямую KN (принадлежащую сечению) с ребром D₁C₁, они лежат в одной плоскости A₁B₁C₁D₁, получим точку X₃;

Точки X₂ и X₃ лежат в плоскости DD₁C₁C. Проведем прямую X₂ X₃ , которая пересечет ребро C₁C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.

MKNTPL - искомое сечение.

Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты . Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.

Грани, пересекаясь, образуют ребра .
Ребра, пересекаясь, образуют вершины .
Рассмотрим два основных вида многогранников:

Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.

Упражнение

Дана пирамида, основание которой параллельно π₁. Основание представляет собой некоторый треугольник.

S – вершина пирамиды (Рисунок 6.1).

Рисунок 6.1 – Пересечение поверхности пирамиды прямой

Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.

Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.

Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).

Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции необходимо выполнять при помощи пропорционального деления отрезка.

В сечении находим точки M и N принадлежащие прямой m.
Определяем видимость прямой m.

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.

Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.

Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).

Рисунок 6.2 – Построение развёртки пирамиды

В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки \overline,\overline,\overline , проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.

6.2. Призма. Развертка призмы

Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.

Упражнение

Дана призма, основания которой параллельны плоскости проекций π₁.

Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).

Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
В сечении находим точки K и L принадлежащие прямой m.
Определяем видимость прямой m. Если грань АВ на π₂ видна, то точка К на π₂ видима, грань ВС невидима, следовательно, точка Lневидима.

Рассмотрим наклонную призму. Пусть основание призмы параллельно π₁, а ребра параллельны π₂.

Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).

Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

Рисунок 6.4 – Построение развёртки призмы
Порядок построения :

Найдем истинную величину сечения – (1₀2₀3₀), для чего повернём сечение (123) вокруг оси n⊥π₂, (можно ввести ДПП π₃//σ).
Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
/1₀-2₀/; /2₀-3₀/; /3₀-1₀/.

Проведём направления рёбер перпендикулярно этой линии через точки: 1₀; 2₀; 3₀ и отмерим вверх и вниз расстояния от нормального сечения (на π₂) до верхнего и нижнего основания, откладывая их на линиях-ребрах.

6.3. Взаимное пересечение многогранников

В результате пересечения многогранников получим ломаную линию.

Возможны два случая пересечения многогранников (Рисунок 6.5):

Рисунок 6.5 – Варианты пересечения многогранников

Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.

Звенья ломаной – линии пересечения граней.

Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.

Построенные точки соединить.

Упражнение

Построить линии пересечения призмы с пирамидой (Рисунок 6.6).

Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение

Находим на π₂ проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 1₂ и 2₂). Находим их горизонтальные проекции.
Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 3₂ и 4₂), для чего используем вспомогательную плоскость τ⊥π₂.
Полученные на π₁ точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 1₁-3₁, 1₁-2₁, 1₁-4₁ невидимы. Получили замкнутую линию пересечения пирамиды с призмой.

Упражнение

остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).

По двум проекциям построить третью;
На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
Построить развёртку пирамиды с нанесением линии пересечения.

Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение :

Проводим линии рёбер призмы на всех проекциях.
Введём плоскость σ⊥π₂, σ//π₁:

σ//АВС – основанию пирамиды;
σ пересекает пирамиду сечение подобно ΔА₁В₁С₁.

Это сечение пересекается:

— с ребром D в двух точках 1 и 4;

— с ребром Е в двух точках 2 и 5.

Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.

Построение развертки рассмотрено ранее.

6.4. Задачи для самостоятельной работы

1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).

Рисунок 6.8

Рисунок 6.9

Рисунок 6.10

Рисунок 6.11

рассмотреть основные простейшие виды сечений призмы, рассмотреть теорию метода следов и применить ее для построения более сложных сечений.

Воспитательные: воспитание самостоятельности, умения слушать, анализировать и делать выводы

Развивающие: развитие пространственного воображения, навыков самоорганизации, работы в парах при выполнении домашнего задания, умения анализировать, обобщать и делать выводы.

Оборудование: компьютер, мультимедийный проектор, доска и мел.

Учитель: Прежде чем говорить об актуальности темы, давайте ответим себе на несколько вопросов:

Что такое многогранник?

Ответ: Многогранник это тело, поверхность которого состоит из нескольких многоугольников.

Что такое призма?

Ответ: призма это многогранник, состоящий из двух многоугольников, лежащих в параллельных плоскостях и совмещаемых параллельным переносом и всех отрезков соединяющих соответствующие точки этих многоугольников.

Что такое сечение?

Ответ: Сечением поверхности геометрических тел называется плоская фигура, полученная в результате пересечения тела плоскостью и состоящая из точек принадлежащих как секущей плоскости так и из точек самой поверхности данного тела.

Вот теперь поговорим, для чего нужны сечения и где они встречаются?

В математике нет ни одной темы, которая бы не находила своего широкого применения на практике. Так вот, построение сечений не является исключением. Очень часто с сечение различных геометрических тел встречаются в инженерии, в строительстве итд. Более того, порой недостаточно уметь просто строить эти сечения, а также необходимо уметь вычислять например площадь или периметр этого сечения. Так же задания на построение сечений и вычисление его элементов встречаются в программе профильного уровня ЕГЭ в рамках задачи №16, и как показывает практика, эти задания вызывают большие трудности у выпускников. Именно поэтому, изучение данной темы необходимо на достаточно углубленном уровне.

Итак, перейдем к рассмотрению темы и следующий вопрос будет такой:

Каким способом можно задать секущую плоскость?

Через три точки можно провести плоскость и притом только одну

Через прямую и не лежащую на ней точку можно провести плоскость и притом только одну

Через две пересекающиеся прямые можно провести плоскость и притом только одну

Через две параллельные прямые можно провести единственную плоскость.

А сейчас рассмотрим самые простейшие виды сечений призмы:

Это сечение параллельное основаниям. В сечении получается многоугольник, равный основаниям.

На этом чертеже построено сечение призмы плоскостью, параллельной боковой грани. Оно представляет собой параллелограмм.

А на этом чертеже построено так называемое диагональное сечение. Это сечение, проходящее через два боковых ребра, не принадлежащие одной грани. Оно представляет собой параллелограмм.

Для построения более сложных сечений призмы может и пользоваться метод следов, где основа всего метода в следе секущей плоскости.

Следом секущей плоскости называется прямая пересечения секущей плоскости и плоскости основания призмы.

Суть метода следов состоит в применении ряда правил построения сечений:

Пусть дана пятиугольная призма, точка А, принадлежащая верхнему основанию призмы и секущей плоскости и след а секущей плоскости, принадлежащий плоскости нижнего основания.

Тогда пересечение секущей плоскости верхнего основания будет представлять собой отрезок СД, проходящий через точку А, параллельный следу а.

Пусть снова дана пятиугольная призма. Если точка А принадлежит боковой грани, то пересечение этой грани с секущей плоскостью, проходящей через точку А строится так:

Строим точку В, в которой плоскость грани, пересекает след а

Затем проводим прямую АВ. Она пересекает грань по отрезку СД.

Отрезок СД и есть пересечение этой грани с секущей плоскостью, проходящей через точку А

Если грань, содержащая точку А параллельна следу а, то секущая плоскость, пересекающая эту грань и проходящая через точку А,пересекает эту грань по отрезку СД, параллельному следу а.

Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение этих граней с секущей плоскостью. Таким образом можно получить многоугольник, который и окажется сечением призмы. В использовании этих трех правил и состоит суть метода следов для построения сечения призмы.

Построить сечение четырехугольной призмы плоскостью, проходящей через прямую а, лежащей в плоскости нижнего основания и точку Н, принадлежащей боковому ребру.

Очевидно, что прямая а это и есть след секущей плоскости.

Точка Н принадлежит грани (АВВ₁), поэтому строим точку Р, в которой плоскость этой грань пересекает след а.а именно след пересекает прямая АВ. затем строим прямую РН, которая пересечет данную грань по отрезку НМ.

Далее, так как точка М принадлежит грани (ВСС₁),то проводим ВС, которая пересечет след в точке Q. Проводим QM, пересекающую грань по отрезку MN.

Точка N принадлежит грани (СДД₁), поэтому проводим СД пересекающую след а в точке Z, затем проводим ZN, пересекающую грань призмы по отрезку NV.

Точки Nи V лежат в одной грани, поэтому проводим прямую NV.

Четырехугольник HVNV – искомое сечение.

Теперь попробуйте выполнить аналогичное задание.

Постройте сечение шестиугольной призмы плоскостью, проходящей через точку на одном из боковых ребер и прямую, лежащую в плоскости нижнего основания.( ученик выходит к доске для решения задачи)

Теперь рассмотрим еще одну задачу.

Построить сечение четырехугольной призмы плоскостью, проходящей через точку А, лежащую в плоскости верхнего основания и прямую, лежащую в плоскости нижнего основания.

По данному чертежу попробуйте сделать описания хода решения, используя правило №1. (для описания ученик выходит к доске и по чертежу расписывает пошагово ход решения)

Понятно ли вам как строить сечения призмы методом следов?

В чем состоит сложность этого метода именно для вас?

Как вы считаете, всегда ли след плоскости дается в условии?

Так вот, оказывается, что след плоскости в условии дается далеко не всегда. В этом случае этот след необходимо построить, что естественно значительно осложняет решение задачи. Но когда след будет построен, то дальнейшее построение сечения выполняется по общей методике,т.е именно так как мы сегодня строили. Такие задачи мы с вами будем решать на следующем уроке. Не останутся без нашего внимания также и простейшие сечения. например, диагональные. Мы научимся находить площади и периметры таких сечений, а также разберем основные типы задач №16 из бланков профильного уровня ЕГЭ. Но это все на последующих уроках. А сегодня нам было необходимо рассмотреть метод следов. Запишите домашнее задание:

Изучить теоретический материал, котрый мы сегодня рассмотрели.

Построить сечение пятиугольной призмы плоскостью, проходящей через точку М на боковом ребре и прямую лежащую в плоскости нижнего основания.

Построить сечение четырехугольной призмы плоскостью, проходящей через точку в плоскости верхнего основания и прямую, лежащую в плоскости нижнего основания.( используйте правило №1)

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение призмы

Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.

На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.

Элементы призмы

Для рисунка выше:

Основания

ABCD

A₁B₁C₁D₁

Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:

Примечание: свойства призмы представлены в отдельной публикации.

Варианты сечения призмы

Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.

ЗАДАЧА 1.Построить сечение призмы плоскостью общего положения и построить истинный вид сечения.

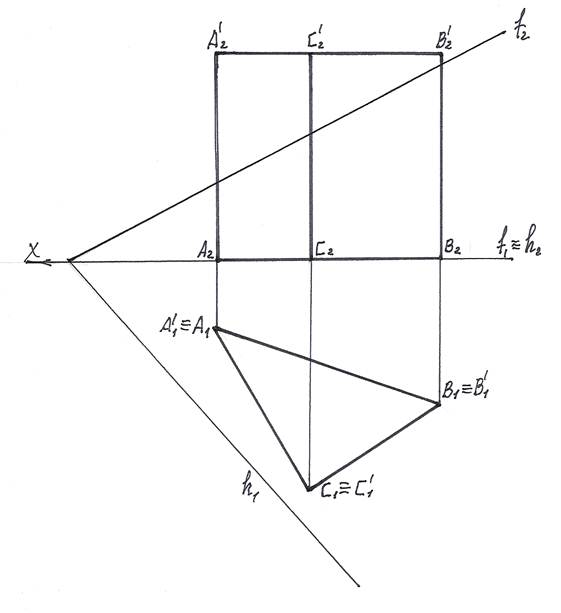
1). Для преобразования секущий пл. Г общего положения в плоскость прое-цирующую введем вместо пл. П₂ новую пл. П₄ так, чтобы она была перпендику-лярна плоскости П₁ и проходила перпендикулярно горизонтали h секущей пл. Г.

На чертеже новую ось Х_1,4 проводим перпендикулярно горизонтальной проекции горизонтали. Х_1,4 ^ h₁.

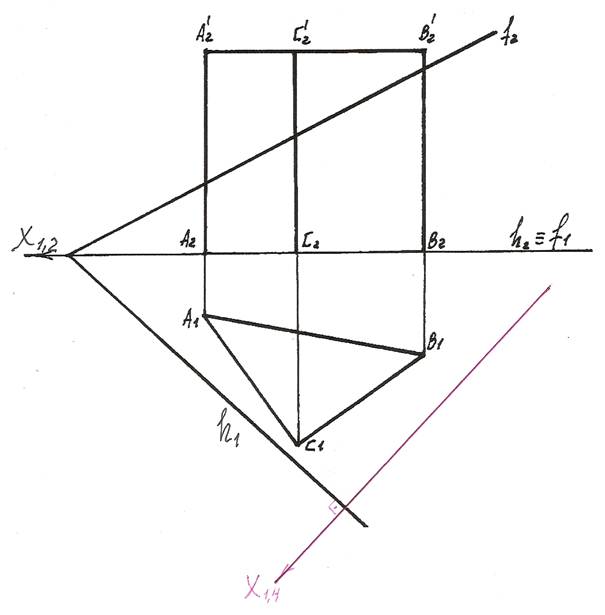
2). В плоскости П₄ строим новую фронтальную проекцию призмы АВСА'В'С'.

Для этого проводим из А₁, В₁, С₁, А'₁, В'₁, С'₁ линии проекционных связей, перпендикулярные оси Х_1,4, и на их продолжении от новой оси Х_1,4 откладываем координаты Z точек А, В, С, А', В', С'.

Соединив полученные точки, получим новую фронтальную проекцию призмы.

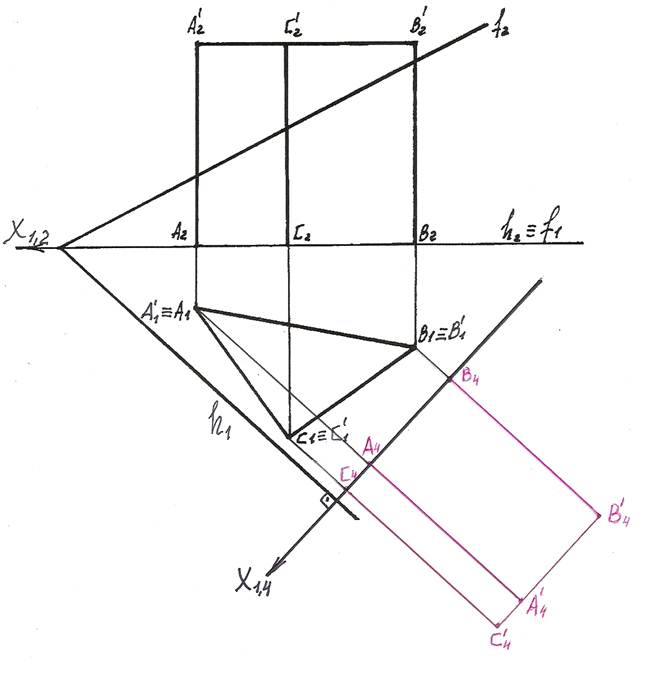
3). В новой системе плоскостей проекций П₁/П₄ секущая плоскость Г по построению фронтально - проецирующая, а значит, ее фронтальная проекция Г₄ – прямая.

Для построения прямой достаточно иметь две точки, например М и N. Пусть точка М – точка пересечения фронтали и горизонтали плоскости Г.

М₁ ≡ М₂. Точку N возьмем произвольно на фронтали f. N₂ Î f₂.

По принадлежности к f построим горизонтальную N₁ проекцию точки N. N₁ Î f₁.

Из М₁ и N₁ проводим линии проекционных связей, перпендикулярные оси Х_1,4 и

на их продолжении от новой оси откладываем отрезки, равные координатам Z

Прямая М₄N₄ – новая фронтальная проекция секущей плоскости Г.

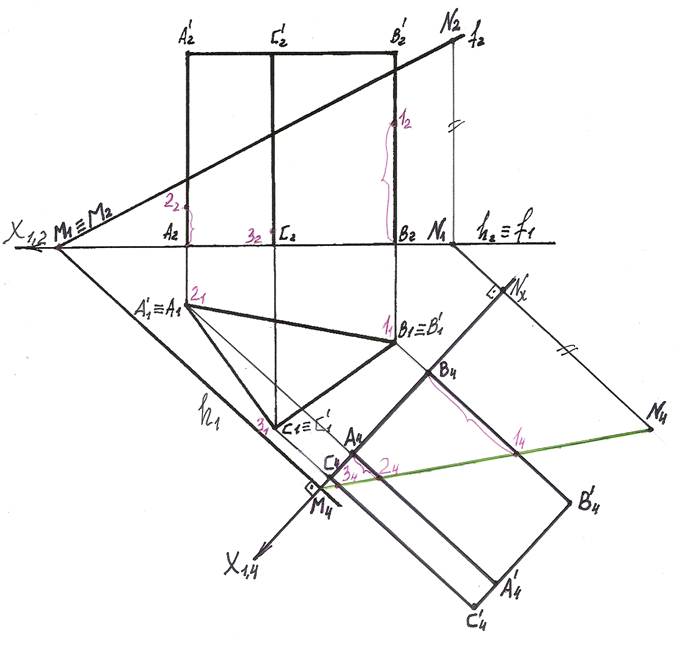
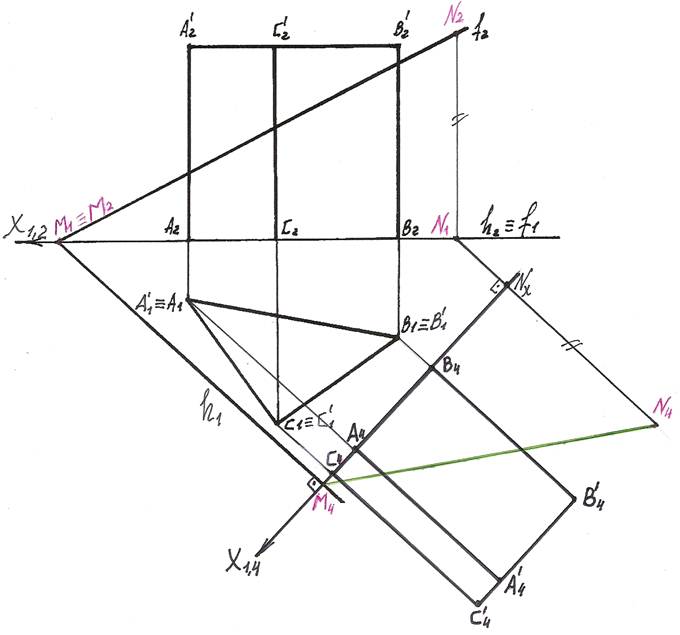
4). На пересечении фронтальной проекции М₄N₄ секущей плоскости Г и ребер

призмы определяем вершины сечения 1₄, 2₄, 3₄.

По принадлежности точек 1, 2 и 3 к соответствующим ребрам определяем их

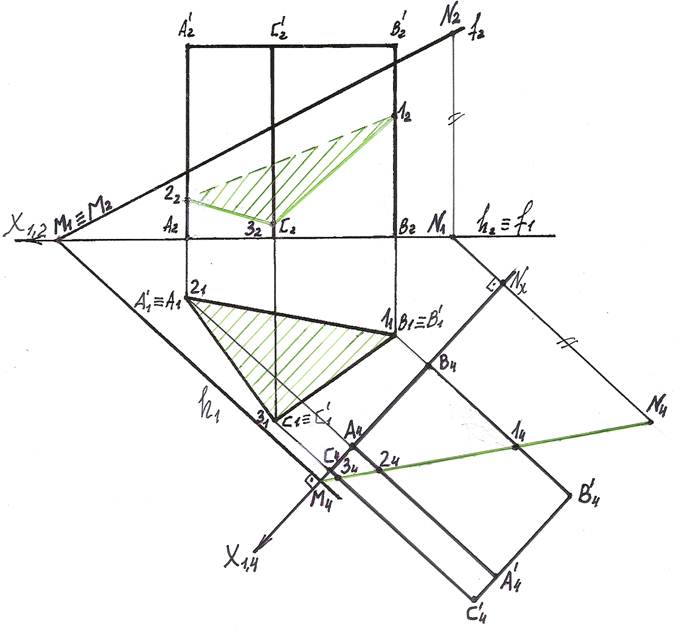
5). Соединяем полученные точки и получаем проекции сечения призмы плоскостью общего положения.

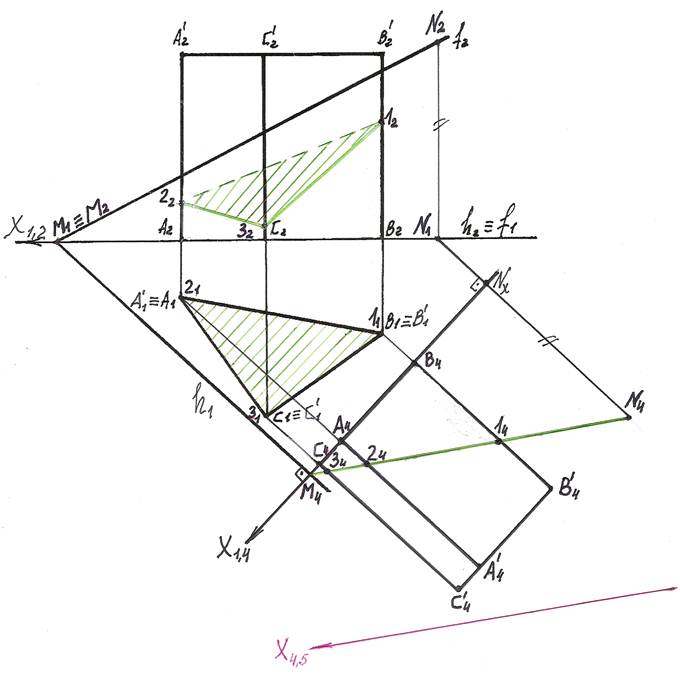
6). Для определения натуральной величины сечения введем еще одну вспомогатель-

На чертеже ось Х_4,5 параллельна следу М₄N₄ секущей плоскости Г.

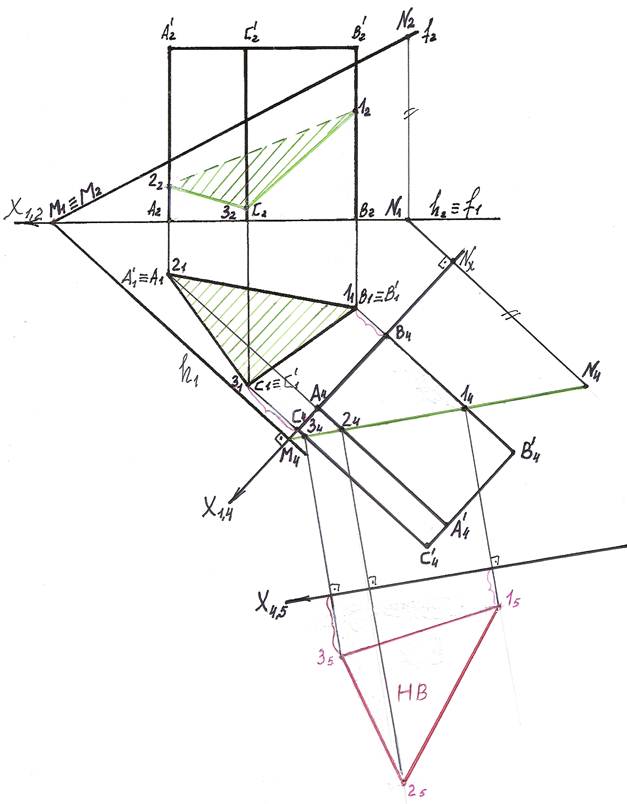
7). В новую плоскость П₅ проецируем точки 1, 2 и 3. Для этого из 1₄, 2₄, 3₄ про-водим линии проекционных связей, перпендикулярные к оси Х_4,5 и на их продолжении откладываем отрезки, равные расстояниям от оси Х_1,4 до заме-няемых точек 1₁, 2₁, 3₁ (В₄1₁, А₄2₁, С₄3₁). Получаем точки 1₅, 2₅, 3₅.

Задача 2. Построить сечение пирамиды SABС плоскостью общего положения

Т (h∩f) и найти его натуральную величину (рис.162).

Задача решается в следующей последовательности:

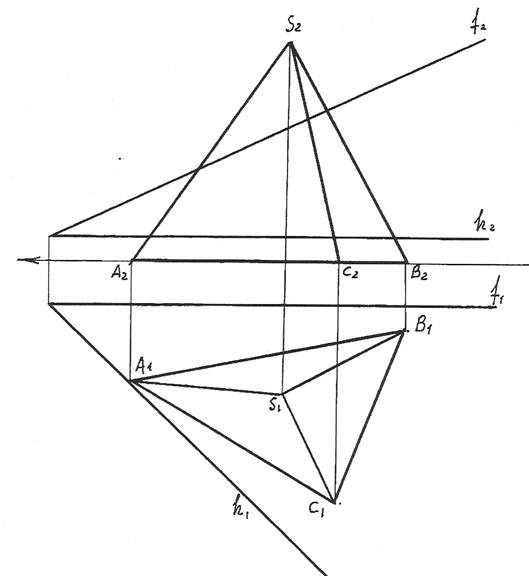
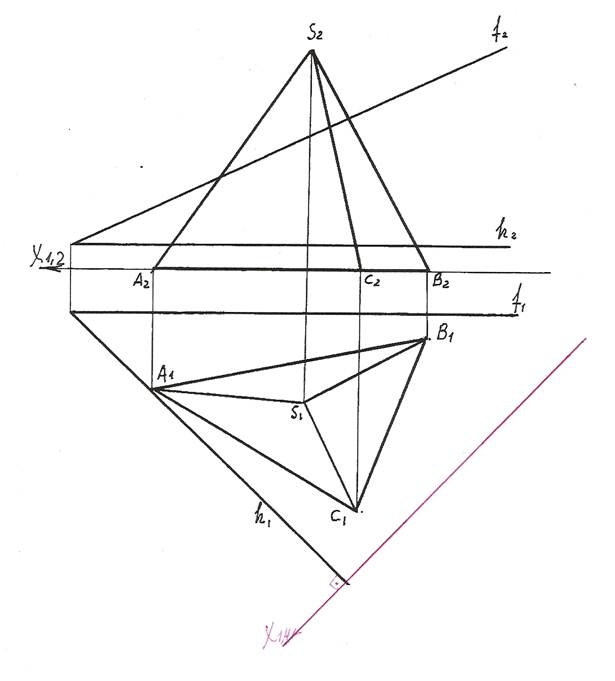
1). Для преобразования секущий пл. Т общего положения в плоскость прое-цирующую введем вместо пл. П₂ новую пл. П₄ так, чтобы она была перпен-дикулярна оставшейся плоскости П₁ и проходила перпендикулярно горизонтали h секущей пл. Т. П₂ ® П₄, П₄ ^ П₁, П₄ ^ h.

На чертеже новую ось Х_1,4 проводим перпендикулярно горизонтальной проекции горизонтали. Х_1,4 ^ h₁.

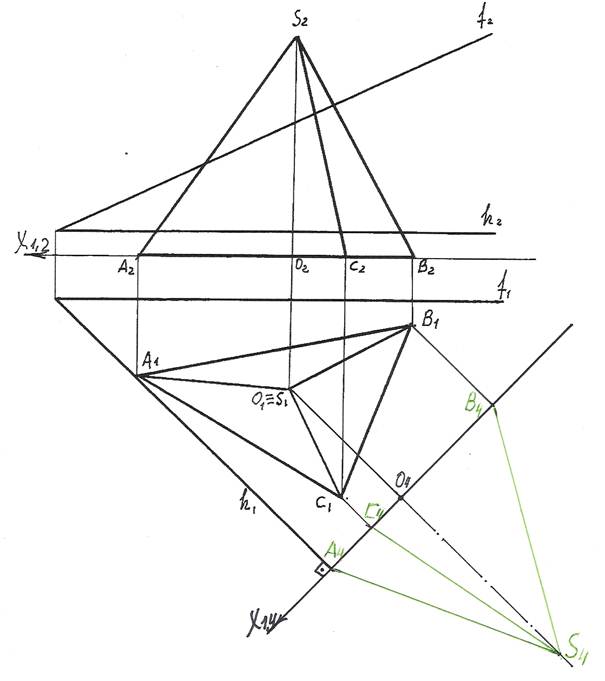
2). Теперь в плоскости П₄ строим новую проекцию S₄A₄B₄C₄ пирамиды SABC. Для этого из горизонтальных проекций A₁, B₁, C₁, S₁ точек A, B, C, S проводим линии проекционных связей, перпендикулярные оси Х_1,4 и на их продолжении от новой оси откладываем координаты Z этих точек. Z_А = Z_В = Z_С = 0; Z_S = O₂S₂.

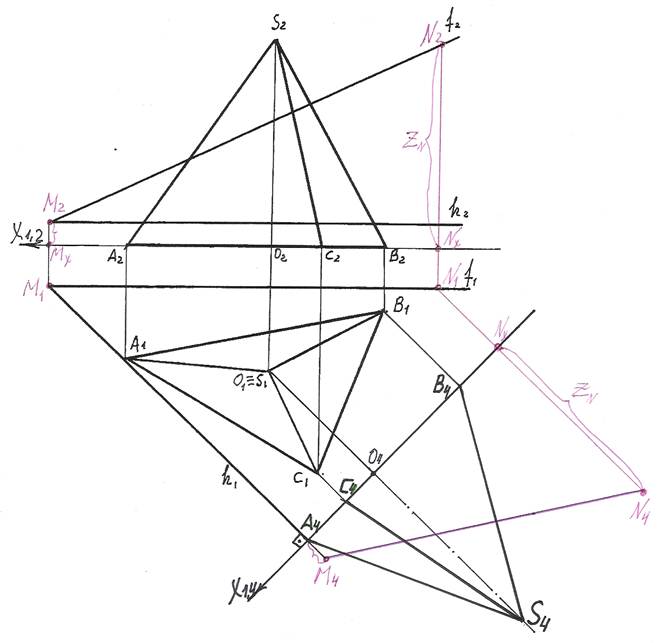
3). Затем строим новую проекцию секущей плоскости Т. Так как в новой системе плоскостей проекции П₁/П₄ секущая плоскость стала фронтально - проецирующей, то ее фронтальная проекция Т₄ – прямая. Построить ее можно по двум точкам, положим, по точке М – точке пересечения фронтали и горизонтали и точке N, произвольно взятой на фронтали N₂ Î f₂.

По принадлежности к фронтали f построим горизонтальную N₁ проекцию т.N.

N₁ Î f₁. Из М₁ и N₁ проводим линии проекционных связей, перпендикулярные оси Х_1,4 и на их продолжении от новой оси откладываем отрезки, равные коорди-натам Z точек М и N. Z_М = М_ХМ₂, Z_N = N_ХN₂. Получаем точки М₄ и N₄.

Прямая М₄N₄ – новая фронтальная проекция секущей плоскости Т.

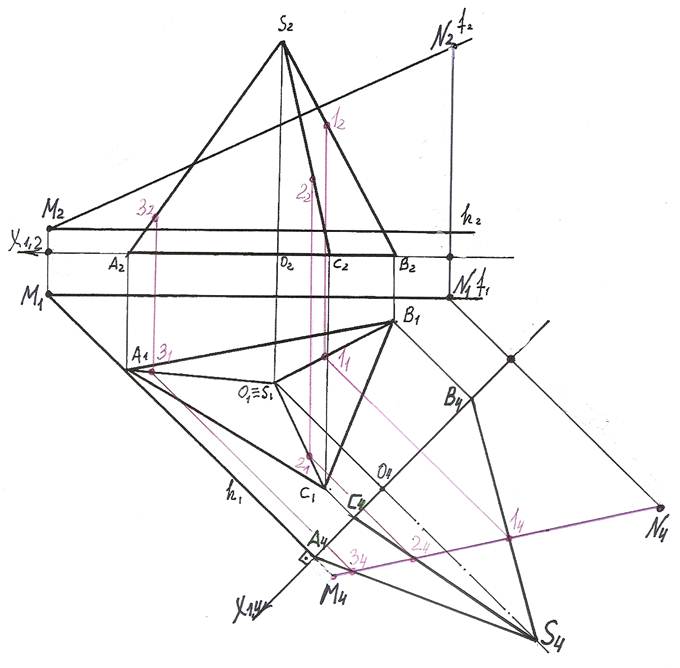
4). Вершины сечения лежат на пересечении фронтальной проекции M₄N₄ плоскости Т с новыми фронтальными проекциями ребер.

Горизонтальные проекции точек 1, 2, 3 получим по принадлежности их к соответствующим ребрам. 1₁ Î В₁S₁, 2₁ Î C₁S₁, 3₁ Î A₁S₁.

Фронтальные проекции 1₂, 2₂, 3₂ точек 1, 2, 3 также строим по принадлежности их к соответствующим ребрам. 1₂ Î В₂S₂, 2₂ Î C₂S₂, 3₂ Î A₂S₂.

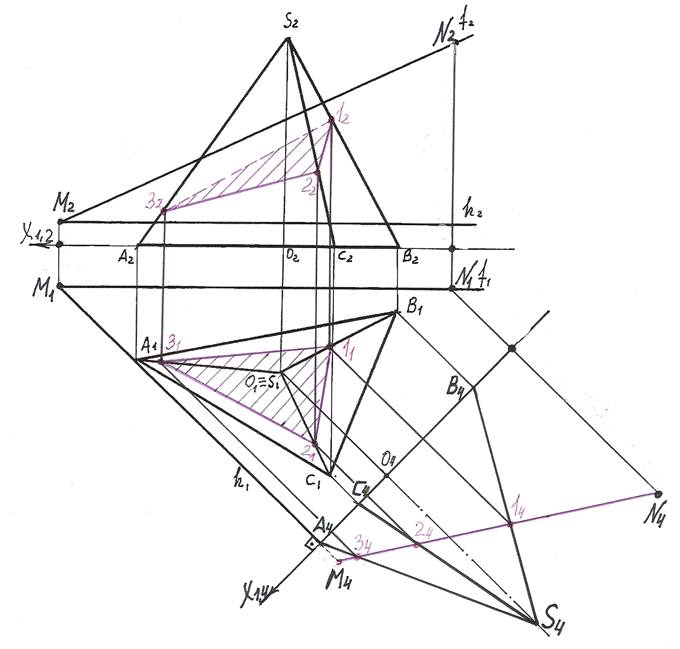
Соединяем точки 1₁, 2₁, 3₁ – получаем горизонтальную проекцию сечения.

Соединяем точки 1₂, 2₂, 3₂ – получаем фронтальную проекцию сечения.

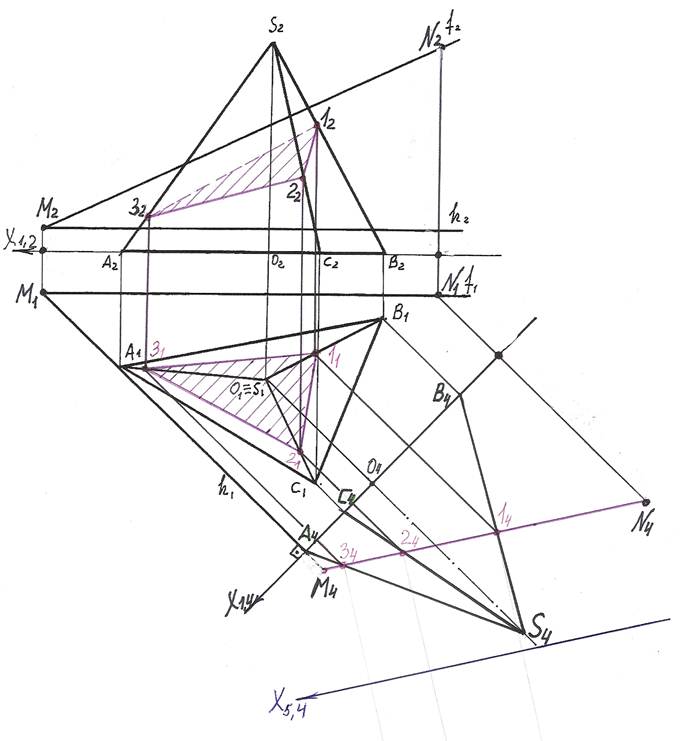
5). Далее, для определения натуральной величины сечения необходимо секущую плоскость преобразовать в плоскость уровня.

Для этого вместо плоскости П₁ вводим новую плоскость П₅, перпендикулярно оставшейся плоскости П₄ так, чтобы она прошла параллельно секущей плоскости.

На чертеже новая ось Х_4,5 пройдет параллельно следу M₄N₄ секущей плоскости Т.

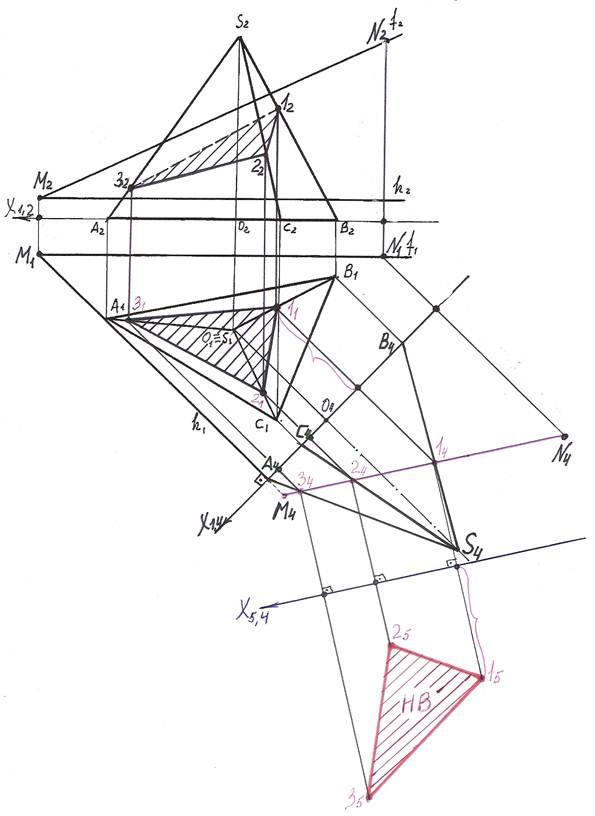
6). В новую плоскость П₅ проецируем вершины сечения, точки 1, 2, 3. Для этого из точек 1₄, 2₄, 3₄ проводим линии проекционных связей, перпендикулярные оси Х_4,5 и на их продолжении от новой оси Х_4,5 откладываем отрезки, равные расстояниям

от оси Х_1,4 до заменяемых точек 1₁, 2₁, 3₁ (координаты Y точек 1,2,3). Получаем точки 1₅, 2₅, 3₅; соединив эти точки получаем натуральную величину треугольника

Читайте также: