Как сделать размах
Обновлено: 04.07.2024
Во-первых, в подавляющем большинстве книг, интернет-ресурсов и уроков по Data Science нюансы, изъяны разных типов нормализации данных и их причины либо не рассматриваются вообще, либо упоминаются лишь мельком и без раскрытия сути.
И, в-третьих, мне всегда хотелось получить универсальный метод учитывающий проблемные места.
Повторение — мать учения
Нормализация — это преобразование данных к неким безразмерным единицам. Иногда — в рамках заданного диапазона, например, [0..1] или [-1..1]. Иногда — с какими-то заданным свойством, как, например, стандартным отклонением равным 1.
Ключевая цель нормализации — приведение различных данных в самых разных единицах измерения и диапазонах значений к единому виду, который позволит сравнивать их между собой или использовать для расчёта схожести объектов. На практике это необходимо, например, для кластеризации и в некоторых алгоритмах машинного обучения.
Аналитически любая нормализация сводится к формуле
где — текущее значение,
— величина смещения значений,
— величина интервала, который будет преобразован к “единице”
По сути всё сводится к тому, что исходный набор значений сперва смещается, а потом масштабируется.
Минимакс (MinMax). Цель — преобразовать исходный набор в диапазон [0..1]. Для него:
= , минимальное значение исходных данных.
= — , т.е. за “единичный” интервал берется исходный диапазон значений.
Стандартизация. Цель — преобразовать исходный набор в новый со средним значением равным 0 и стандартным отклонением равным 1.
= , среднее значение исходных данных.
— равен стандартному отклонению исходного набора.
Для других методов всё аналогично, но со своими особенностями.
В большинстве методов кластеризации или, например, классификации методом ближайших соседей необходимо рассчитывать меру “близости” между различными объектами. Чаще всего в этой роли выступают различные вариации евклидового расстояния.
Представим, что у Вас есть какой-то набор данных с несколькими признаками. Признаки отличаются и по типу распределения, и по диапазону. Чтобы можно было с ними работать, сравнивать, их нужно нормализовать. Причём так, чтобы ни у какого из них не было преимуществ перед другими. По крайней мере, по умолчанию — любые такие предпочтения Вы должны задавать сами и осознанно. Не должно быть ситуации, когда алгоритм втайне от Вас сделал, например, цвет глаз менее важным, чем размер ушей*
* нужно сделать небольшое примечание — здесь речь идёт не о важности признака для, например, результата классификации (это определяется на основе самих данных при обучении модели), а о том, чтобы до начала обучения все признаки были равны по своему возможному влиянию.
Итого, главное условие правильной нормализации — все признаки должны быть равны в возможностях своего влияния.
Шаг 1 — определяем смещение
Чаще всего данные центрируют — т.е. определяют, значение, которое станет новым 0 и “сдвигают” данные относительно него.
Здесь проявляется проблема № 1 — различные типы распределений не позволяют применять к ним методы, созданные для нормального распределения.
Если Вы спросите любого специалиста по статистике, какое значение лучше всего показывает “типичного представителя” совокупности, то он скажет, что это — медиана, а не среднее арифметическое. Последнее хорошо работает только в случае нормального распределения и совпадает с медианой (алгоритм стандартизации вообще оптимален именно для нормального распределения). А у Вас распределения разных признаков могут (и скорее всего будут) кардинально разные.
Вот, например, различия между медианой и средним арифметическим значением для экспоненциального распределения.

А вот так выглядят эти различия при добавлении выброса:

В отличии от среднего значения медиана практически не чувствительна к выбросам и асимметрии распределения. Поэтому её оптимально использовать как “нулевое” значение при центрировании.
В случае, когда нужно не центрировать, а вписать в заданный диапазон, смещением является минимальное значение данных. К этому вернёмся чуть позже.
Шаг 2 — масштабируем
Мы определили нужные величины смещения для всех признаков. Теперь нужно сделать признаки сравнимыми между собой.
Степень возможного влияния признаков определяется величиной их диапазонов после масштабирования. Если оба признака распределены в одинаковых интервалах, например, [-1..1], то и влиять они могут одинаково. Если же изначально один из признаков лежит в диапазоне [-1..1], а второй — в [-1..100], то очевидно, что изменения второго могут оказывать существенно большее влияние. А значит он будет в привилегированном положении по сравнению с первым.
Стандартное отклонение
Вернёмся к примеру стандартизации. В её случае новый диапазон определяется величиной стандартного отклонения. Чем оно меньше, тем диапазон станет “шире”.
Посмотрим на гипотетические распределения различных признаков с одинаковыми начальными диапазонами (так будет нагляднее):

Для второго признака (бимодальное распределение) стандартное отклонение будет больше, чем у первого.

А это значит, что у второго признака новый диапазон после масштабирования (стандартизации) будет “уже”, и его влияние будет меньше по сравнению с первым.

Итог — стандартное отклонение не удовлетворяет начальным требованиям по одинаковому влиянию признаков (величине интервала). Даже не говоря о том, что и наличие выбросов может исказить “истинную” величину стандартного отклонения.
Межквартильный интервал
Другим часто используемым кандидатом является разница между 75-м и 25-м процентилями данных — межквартильный интервал. Т.е. интервал, в котором находятся “центральные” 50% данных набора. Эта величина уже устойчива к выбросам и не зависит от “нормальности” распределения наличия/отсутствия асимметрии.
Но и у неё есть свой серьезный недостаток — если у распределения признака есть значимый “хвост”, то после нормализации с использованием межквартильного интервала он добавит “значимости” этому признаку в сравнении с остальными.
Проблема № 2 — большие “хвосты” распределений признаков.
Пример — два признака с нормальным и экспоненциальным распределениями. Интервалы значений одинаковы

После нормализации с использованием межквартильного интервала (для наглядности оба интервала смещены к минимальным значениям равным нулю).

В итоге интервал у признака с экспоненциальным распределением из-за большого “хвоста” стал больше. А, следовательно, и сам признак стал “влиятельнее”.
Размах значений
Очевидным решением проблемы межквартильного интервала выглядит просто взять размах значений признака. Т.е. разницу между максимальным и минимальным значениями. В этом случае все новые диапазоны будут одинаковыми — равными 1.
И здесь максимально проявляется, наверное, самая частая проблема в подготовке данных, проблема № 3 — выбросы. Присутствие одного или нескольких аномальных (существенно удалённых) значений за пределами диапазона основных элементов набора может ощутимо повлиять на его среднее арифметическое значение и фиктивно увеличить его размах.
Это, пожалуй, самый наглядный пример из всех. К уже использовавшемуся выше набору из 2-х признаков добавим немного выбросов для одного признака

После нормализации по размаху

Наличие выброса, который вдвое увеличил размах признака, привело к такому же уменьшению значимого интервала его значений после нормализации. Следовательно влияние этого признака уменьшилось.
Работаем с выбросами
Решением проблемы влияния выбросов при использовании размаха является его замена на интервал, в котором будут располагаться “не-выбросы”. И дальше — масштабировать по этому интервалу.
Искать и удалять выбросы вручную — неблагодарное дело, особенно когда количество признаков ощутимо велико. А иногда выбросы и вовсе нельзя удалять, поскольку это приведёт к потере информации об исследуемых объектах. Вдруг, это не ошибка в данных, а некое аномальное явление, которое нужно зафиксировать на будущее, а не отбрасывать без изучения? Такая ситуация может возникнуть при кластеризации.
Пожалуй, самым массово применяемым методом автоматического определения выбросов является межквартильный метод. Его суть заключается в том, что выбросами “назначаются” данные, которые более чем в 1,5 межквартильных диапазонах (IQR) ниже первого квартиля или выше третьего квартиля.*
* — в некоторых случаях (очень большие выборки и др.) вместо 1,5 используют значение 3 — для определения только экстремальных выбросов.
Схематично метод изображен на рисунке снизу.

Вроде бы все отлично — наконец-то есть инструмент, и можно приступать к работе.
Но и здесь есть своя ложка дёгтя. В случае наличия длинных хвостов (как, например, при экспоненциальном распределении) слишком много данных попадают в такие “выбросы” — иногда достигая значений более 7%. Избирательное использование других коэффициентов (3 * IQR) опять приводит к необходимости ручного вмешательства — не для каждого признака есть такая необходимость. Их потребуется по отдельности изучать и подбирать коэффициенты. Т.е. универсальный инструмент опять не получается.
Ещё одной существенной проблемой является то, что этот метод симметричный. Полученный “интервал доверия” (1,5 * IQR) одинаков как для малых, так и для больших значений признака. Если распределение не симметричное, то многие аномалии-выбросы с “короткой” стороны просто будут скрыты этим интервалом.

Скорректированный интервал
Красивое решение этих проблем предложили Миа Хаберт и Елена Вандервирен (Mia Hubert and Ellen Vandervieren) в 2007 г. в статье “An Adjusted Boxplot for Skewed Distributions”.
Их идея заключается в вычислении границ “интервал доверия” с учетом асимметрии распределения, но чтобы для симметричного случая он был равен всё тому же 1,5 * IQR.
Для определения некоего “коэффициента асимметрии” они использовали функцию medcouple (MC), которая определяется так:


Поиск подходящей формулы для определения границ “интервала доверия” производился с целью сделать долю, приходящуюся на выбросы, не превышающей такую же, как у нормального распределения и 1,5 * IQR — приблизительно 0,7%
В конечном итоге они получили такой результат:


Более подробно про этот метод и его эффективность лучше прочитать в самой статье. Найти ее по названию не составляет труда.
Универсальный инструмент
Теперь, объединяя все найденные плюсы и учитывая проблемы, мы получаем оптимальное решение:
- Центрирование, если оно требуется, производить по медиане.
- Масштабировать набор данных по величине скорректированного интервала.
- (Опционально) — если центрирование не требуется, то смещать масштабированные данные так, чтобы границы скорректированного интервала приходились на [0..1]
Назовем его методом… скорректированного интервала — по названию статьи Mia Hubert и Ellen Vandervieren
Теперь сравним результаты обычных методов с новым. Для примера возьмем уже использовавшиеся выше три распределения с добавлением выбросов.

Сравнивать новый инструмент будем с методами стандартизации, робастной нормализации (межквартильный интервал) и минимакса (MinMax — с помощью размаха).
Ситуация № 1 — данные необходимо центрировать. Это используется в кластеризации и многих методах машинного обучения. Особенно, когда необходимо определять меру “близости” объектов.

Робастная нормализация (по межквартильному интервалу):


Преимущество использования метода скорректированного интервала в том, что каждый из признаков равен по своему возможному влиянию — величина интервала, за пределами которого находятся выбросы, одинакова у каждого из них.
Ситуация № 2 — данные необходимо вписать в заданный интервал. Обычно это [0..1]. Это используется, например, при подготовке данных для входов нейронной сети.
MinMax (по размаху):


В этом случае метод скорректированного интервала вписал в нужный диапазон только значения без выбросов. Значения-выбросы, выходящие за границы этого диапазона, в зависимости от постановки задачи можно удалить или принудительно приравнять ближайшей границе нужного диапазона — т.е. 0 или 1.
То, что только “нормальные” данные попадают в единичный диапазон [0..1], а выбросы не удаляются, но пропорционально выносятся за его пределы — это крайне полезное свойство, которое сильно поможет при кластеризации объектов со смешанными признаками, как числовыми, так и категорийными. Подробно об этом я напишу в другой статье.
Напоследок, для возможности пощупать руками этот метод, Вы можете попробовать демонстрационный класс AdjustedScaler из моей библиотеки AdjDataTools.
Он не оптимизирован под работу с очень большим объемом данных и работает только с pandas DataFrame, но для пробы, экспериментов или даже заготовки под что-то более серьезное вполне подойдет. Пробуйте.
Вводить можно целые(1, 2, 3, -7), десятичные(0.25, -1.15), дробные(-1/8, 32/9). Если необходимо ввести смешанное число, то нужно перед вводом перевести его в неправильную обыкновенную дробь. Т.е. 1 целая 1/2 вводить нужно будет как 3/2.
При вводе десятичных дробей использовать точку. Запятая зарезервирована под разделитель.
В качестве разделителя можно использовать любой символ кроме цифр(0-9), слэша(/), точки(.), знака минус(-). Остальные символы и перенос строки будут программой заменены на разделители.
Определение размаха вариации
Размах вариации это разность между наибольшим и наименьшим значением признака в изучаемой совокупности.

Урок начинаем с примера, с помощью которого вводим понятие среднего арифметического числового ряда. Таким же образом, то есть на примерах, вводим понятия размаха ряда и моды ряда. Также на уроке говорим, где находят применение рассмотренные статистические характеристики.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Среднее арифметическое, размах и мода"
· разобрать, где находят применение рассмотренные статические характеристики.
Давайте рассмотрим пример.
Ежедневно в течение 10 дней в полдень измеряли температуру воздуха (в градусах Цельсия) и получили следующие данные.
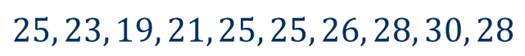
Пользуясь этим рядом, мы можем определить среднюю температуру воздуха, наблюдаемую в течение этих десяти дней.
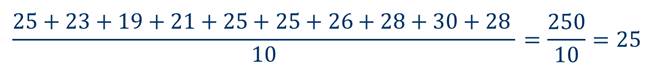
Число 25 называют средним арифметическим рассматриваемого ряда чисел.
Определение.
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
Таким образом, умея находить среднее арифметическое ряда чисел, мы можем найти средний расход холодной воды семьёй в течение года

средний балл ученика за четверть

среднюю урожайность пшеницы за последние 5 лет и так далее.

Вернёмся к нашему примеру. Обратите внимание, что температура воздуха в некоторые дни существенно отличается от 25 градусов Цельсия (то есть от средней температуры). Так, самая высокая температура равна 30 градусам, а самая низкая – 19 градусам.
Найдём разность между наибольшим и наименьшим значениями:
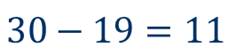
Говорят, что размах ряда равен 11.
Определение.
Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.
Размах ряда находят, когда хотят узнать, насколько велик разброс данных в ряду. Так, например, в нашем примере размах ряда показывает колебание температуры воздуха в течение 10 дней.
Но кроме среднего арифметического и размаха ряда данных, нас может заинтересовать вопрос: какая температура воздуха чаще всего устанавливалась за 10 дней? Заметим, что чаще всего в нашем ряду встречается число 25. Это число называют модой рассматриваемого ряда.
Определение.
Модой ряда называется число, которое встречается в данном ряду чаще других.
Стоит отметить, что ряд может иметь более одной моды.

Также ряд может и не иметь моды.

Моду ряда находят, когда хотят выяснить некоторый характерный показатель. Например, удобно воспользоваться этим показателем при изучении спроса покупателей на мужскую обувь, чтобы определить какой размер самый популярный.
Рассмотрим ещё один пример.

Например, проведя опрос группы людей, можно определить, какой из видов спорта более популярен. И модой будут служить те ответы, которые чаще всего встречаются.

Рассмотренные на уроке характеристики (среднее арифметическое, размах и мода) применяются в статистике.
Определение.
Статистика (от латинского слова статус, что означает состояние, положение вещей) – это наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в обществе и природе.
Основываясь на примерах, которые мы с вами рассматривали на уроке, можно сказать, что статистика используется в различных сферах деятельности человека.

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для полного анализа изучаемого процесса или явления. Иногда совершенно непохожие по своему внутреннему строению совокупности могут иметь равные средние величины. Поэтому для более детального изучения того или иного явления необходимо учитывать разброс или вариацию значений отдельных единиц совокупности. Измерение вариации признаков имеет как теоретическое, так и практическое значение.
Основными показателями, характеризующими вариацию, являются:
1) Размах вариации

2) Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений:


где – абсолютные значения отклонений отдельных вариантов xi от средней арифметической ; fi – частота.
3. Дисперсия – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической:

4. Среднее квадратическое отклонение – корень квадратный из дисперсии:


. В отличие от дисперсии среднее квадратическое отклонение является абсолютной мерой вариации признака в совокупности и выражается в единицах измерения варьирующего признака (руб., тыс., млн и т.д.). .
5. Коэффициент вариации – используется для сравнительной оценки вариации, а также для характеристики однородности совокупности:

Пример. Для иллюстрации расчетов воспользуемся данными нижеприведенной табл. 9.1:
Таблица 9.1 ‑ Данные о продаже основных марок холодильников:
Рассчитаем размах вариации.
R= 1200-460=740$
Пример вычисления размаха вариации
Размах вариации служит незаменимой мерой разброса экстремальных значений признака. Кроме характеристики границ разброса признака, размах вариации может быть использован для выявления ошибок. При наличии очень больших (или очень малых) ошибочно записанных значений признака размах вариации сразу резко возрастает, что требует проверки и корректировки исходных данных.
Недостатком данного показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ. Вследствие этого размах вариации может неправильно характеризовать общую колеблемость признака.
Этого недостатка лишен другой показатель – дисперсия, рассчитываемый как средний квадрат отклонений значений признака от их средней величины.
Между индивидуальными отклонениями от средней и колеблемостью признака существует прямая зависимость: чем сильнее колеблемость признака, тем больше отклонения его значений от средней величины и менее устойчив изучаемый показатель.
Как и средняя величина этот показатель может быть рассчитан в двух формах: взвешенной и невзвешенной
По приведенным выше данным определим средневзвешенную цену холодильника:

Далее рассчитаем дисперсию:

. Следует отметить, что дисперсия еще не дает представления об однородности совокупности, и этому показателю трудно дать экономическую интерпретацию, т.к. он рассчитан в квадратных единицах. Поэтому следующим шагом в исследовании однородности совокупности является расчет среднего квадратического отклонения, показывающего, насколько в среднем отклоняются конкретные варианты признака от его среднего значения. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность что и изучаемый признак. .
Рассчитаем среднее квадратическое отклонение

Вывод: Таким образом, цена каждой марки холодильника отклоняется от средней цены в среднем на 271,1 $
Рассмотренные показатели позволяют получить абсолютное значение вариации признака. Однако для сравнения разных совокупностей с точки зрения устойчивости какого-либо одного признака или для определения однородности совокупности рассчитывают относительные показатели.
Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего эти показатели выражаются в процентах.
Определим значение показателя вариации по вышеприведенным данным таблицы

Совокупность считается однородной, если V не превышает 33%.
Если V 25% – вариация сильная.
Вывод: Рассчитанная величина свидетельствует о неоднородности цен на холодильники, т.к. однородной совокупность считается, если коэффициент вариации меньше 33% (для распределений близких к нормальному).
!! Следует отметить, что коэффициент вариации может быть более 100%, что, в частности, может быть при наличии значений сильно отличающихся от средней величины. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине.
Изучая вариацию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в расчетах, трудно оценить степень воздействия на него какого-либо отдельного признака.
При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным (оказывающим влияние на взаимосвязанный с ним признак) и результативным (подверженным влиянию).
Для выявления взаимосвязи исходная совокупность делится по факторному признаку на группы. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих вариацию индивидуальных значений признака, используют правило сложения дисперсий.
Общая дисперсия представляет собой сумму средней из виутригрупповой и межгрупповой и дисперсий:


Общая дисперсия характеризует вариацию признака по всей совокупности как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности.


Межгрупповая дисперсия характеризует вариацию, обусловленную влиянием фактора, положенного в основу группировки.


Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка. Другими словами внутригрупповая дисперсия отражает случайную вариацию. Внутригрупповая дисперсия рассчитывается отдельно по каждой j-ой группе.


Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующих групп по формуле:

Взаимосвязь между тремя видами дисперсий получила название правила сложения дисперсий. Таким образом, зная два вида дисперсий всегда можно определить третий:

Из этого равенства следует, что общая дисперсия, как правило, будет больше средней из групповых дисперсий. Это обусловлено тем, что при расчленении общей совокупности единиц на части по какому-либо признаку образуются более или менее однородные группы, в результате чего сокращается колеблемость признаков в пределах каждой группы. Это приводит к тому, что средняя из групповых дисперсий оказывается меньше дисперсии признака по всей совокупности единиц, причем разница между этими показателями будет тем больше, чем однороднее получаются группы в результате расчленения общей совокупности.
Теснота связи между факторным и результативным признаками оценивается на основе эмпирического корреляционного отношения:
Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.
Пример. На следующем условном примере исследуем зависимость объема выполненных работ от формы собственности проектно-изыскательских организаций.
Таблица 9.2. Выполнение работ проектно-изыскательскими организациями разной формы собственности
Объем выполненных работ
1) Определим средний объем работ для предприятий двух форм собственности.

2) Определим средний объем работ для каждой формы собственности.

3) Рассчитаем общую и внутригрупповые (т.е. для каждой группы) дисперсии.

4) Определим среднюю из внутригрупповых и межгрупповую дисперсию. Для этого полученные ранее данные заносятся в таблицу расчета.
Таблица 9.3. – Вспомогательная таблица
Пример. Средняя из внутригрупповых дисперсий

Пример. Межгрупповая дисперсия

На последнем этапе решения задачи необходимо проверить тождество, отражающее закон сложения дисперсий:
Проверка закона сложения дисперсий: 54,0+189,8=243,8
Вывод: Таким образом, можно сделать вывод о том, что объем работ, выполненных проектно-изыскательскими организациями на 22% [(54,0/243,8) х 100%] зависит от фактора, положенного в основание группировки, т.е. от формы собственности, а на 78% [(189,8/243,8)х100%)] ‑ от прочих факторов.
Вывод о том, что объем выполненных работ в гораздо большей степени зависит от каких-либо других факторов, чем от формы собственности предприятий подтверждается и величиной эмпирического корреляционного отношения:

Вывод: Величина этого показателя свидетельствует о том, что зависимость объема работ от формы собственности предприятия невелика
Контрольные задания
Вычислить: а) размах вариации; б)среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; относительные показатели вариации возраста студентов.
2. По данным статистических ежегодников постройте таблицу с рядом показателей и определите показатели вариации: а) размах; б) среднее линейное отклонение; в) среднее квадратическое отклонение; г) коэффициент вариации. Оцените количественную однородность совокупности.
Читайте также:

