Как сделать призму черчение

Добавил пользователь Алексей Ф.
Обновлено: 04.10.2024

Построение развертки поверхности призмы можно выполнить несколькими способами:

Способ нормального сечения.
Способ раскатки.
Способ треугольников (триангуляции) — здесь не рассматривается.

Рассмотрим на примерах построение развертки поверхности призмы

первыми двумя способами.

1-й способ. Способ нормального сечения (нормальное сечение перпендикулярно ребрам призмы).

Этот способ развертки боковой поверхности призмы можно применить, если на чертеже:

ребра призмы являются прямыми уровня, то есть имеют на одной из заданных проекций натуральную величину,
на проекциях нет натуральных величин оснований призмы.

. Если на чертеже ребра призмы являются прямыми общего положения, то следует изменить положение призмы относительно плоскостей проекций, преобразовав ребра в прямые уровня, например, способом замены плоскостей проекций.

Построение развертки боковой поверхности призмы способом нормального сечения выполняется по следующему графическому алгоритму:

1-е действие. Провести на проекции призмы, на которую ребра призмы проецируются в натуральную величину, плоскость нормального сечения, перпендикулярную ее ребрам (в произвольном месте по длине ребер).

2-е действие. Построить натуральную величину многоугольника нормального сечения (например, способом замены плоскостей проекций).

3-е действие. Развернуть на свободном поле чертежа натуральный многоугольник сечения в прямую и через точки его вершин провести перпендикулярные прямые — направления ребер.

4-е действие. Отложить на направлениях ребер в обе стороны от линии нормального сечения натуральные отрезки соответствующих ребер.

5-е действие. Соединить построенные конечные точки ребер отрезками прямых и достроить плоскую фигуру развертки боковой поверхности призмы.

6-е действие. Оформить чертеж развертки, проведя линии сгиба в местах расположения ребер тонкими штрихпунктирными линиями с двумя короткими пунктирами.

На рис. 9.1 показан пример построения развертки поверхности треугольной призмы способом нормального сечения, так как на чертеже призмы ее ребра являются горизонтальными прямыми уровня, а основания являются плоскостями общего положения, т. е. не имеют натуральной величины.

Для построения развертки выполнены графические действия предложенного алгоритма.

1-е действие. Провести горизонтально-проецирующую плоскость нормального сечения перпендикулярно горизонтальным проекциям ребер призмы (произвольно по длине ребер).

2-е действие. Способом замены плоскостей проекций построить натуральную величину нормального сечения — треугольник , стороны которого определяют ширину каждой грани призмы.

3-е действие. На свободном поле чертежа треугольник нормального сечения развернуть в горизонтальную линию и отметить натуральные величины его сторон; из отмеченных на линии сечения точек 1, 2, 3 и 1 провести перпендикулярные прямые — направления ребер.

4-е действие. Отложить на проведенных направлениях ребер вверх и вниз отрезки натуральных величин ребер (см. ребро ) взятых с заданной горизонтальной проекции призмы, где ребра имеют натуральную величину.

5-е действие. Соединить отрезками прямых построенные конечные точки ребер и достроить плоскую фигуру развертки.

6-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам призмы тонкими штрихпунктирными линиями с двумя короткими штрихами.

На этом же рис. 9.1 показано также построение на развертке точки , лежащей на грани призмы.

2-й способ. Способ раскатки

Этот способ развертки применяется, если на чертеже:

ребра призмы являются прямыми уровня;
основания призмы (или одно из оснований) лежат в плоскости уровня, т. е. имеют на чертеже натуральную величину.

На рис. 9.2 показан пример построения развертки способом раскатки, так как на чертеже ребра призмы являются фронтальными прямыми, а оба основания лежат в горизонтальных плоскостях уровня и на горизонтальной проекции призмы имеют натуральную величину. За плоскость развертки принята фронтальная плоскость проекций, так как ребра призмы фронтальные прямые.

Построение развертки способом раскатки выполняется по следующему графическому алгоритму:

2-е действие. Повторить последовательное вращение каждой грани
вокруг следующего ребра и совместить каждую грань с плоскостью развертки, построив конечные точки каждого ребра с помощью дуг-засечек, равных следующим сторонам основания и .

3-е действие. Соединить построенные конечные точки ребер отрезками прямых и достроить плоскую фигуру развертки (достроено также одно основание призмы).

4-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам тонкими штрихпунктирными линиями с двумя короткими пунктирами.

На этом же рисунке показано построение на развертке точки , лежащей на грани призмы.

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Дано:
Пересечение пирамиды и призмы
Необходимо:
Построить развертку прямой призмы и показать на ней линию пересечения призмы с пирамидой.

Построение развертки прямой призмы намного легче, чем развертка пирамиды.

Построение развертки призмы

Построение развертки прямой призмы облегчается тем, что все размеры для развертки берутся с эпюр и нам не надо находить натуральные величины ребер призмы. Так как дана прямая призма, то боковые ребра призмы проецируются на фронтальную плоскость проекций в натуральную величину. Ребра оснований прямой призмы параллельны горизонтальной плоскости проекций и проецируются на нее также в натуральную величину.

Решение задач по начертательной геометрии я произвожу в системе автоматизированного проектирования Автокад и Автокад 3D. Данный прием обучения позволит развить пространственное мышление и закрепить владение Автокад.

Алгоритм построения развертки призмы

Проводим горизонтальную прямую.
От произвольной точки G этой прямой откладываем отрезки GU, UE, ЕК, КG равные длинам сторон основания призмы.
Из точек G, U, . восстанавливают перпендикуляры и на них откладывают величины равные высоте призмы. Полученные точки соединяют прямой. Прямоугольник GG1G1G является разверткой боковой поверхности призмы. Для указания на развертке граней призмы из точек U, E, K восставляют перпендикуляры.
Для получения полной развертки поверхности призмы к развертке поверхности пристраивают многоугольники ее оснований.

Для построения на развертке линии пересечения призмы с пирамидой замкнутых ломанных линий 1, 2, 3 и 4, 5, 6, 7, 8 пользуемся вертикальными прямыми.

Одним из фундаментальных объектов в геометрии является многоугольник. Если рассматривать фигуру в трёхмерном пространстве, то с помощью двух таких геометрических тел с шестью углами можно построит правильную шестиугольную призму. При этом боковые грани обязательно будут прямоугольниками. По своему виду такая фигура напоминает пчелиные соты, поэтому она и интересна для изучения архитекторам и математикам.

Общие сведения

Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.

Кроме основания и граней, в состав стереофигуры входит:

высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
боковые рёбра — стороны, являющиеся общими для боковых граней;
вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.

Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.

В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.

Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.

Свойства шестигранника

Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.

Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:

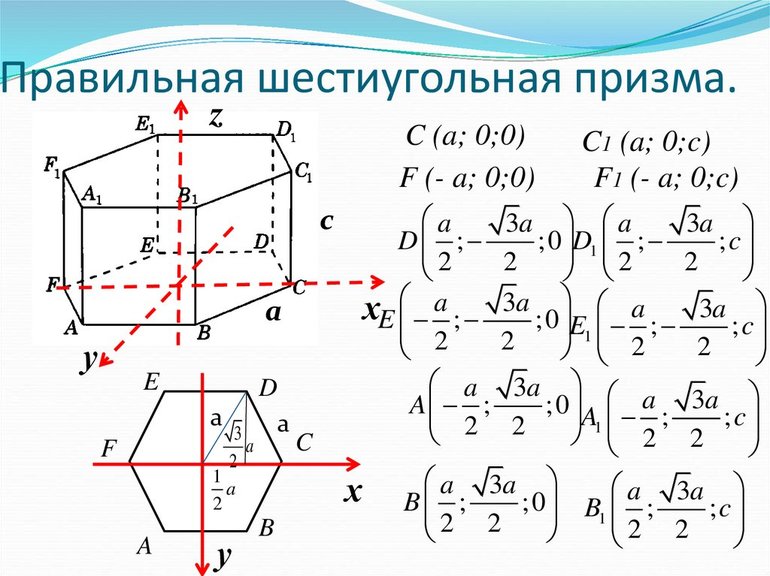
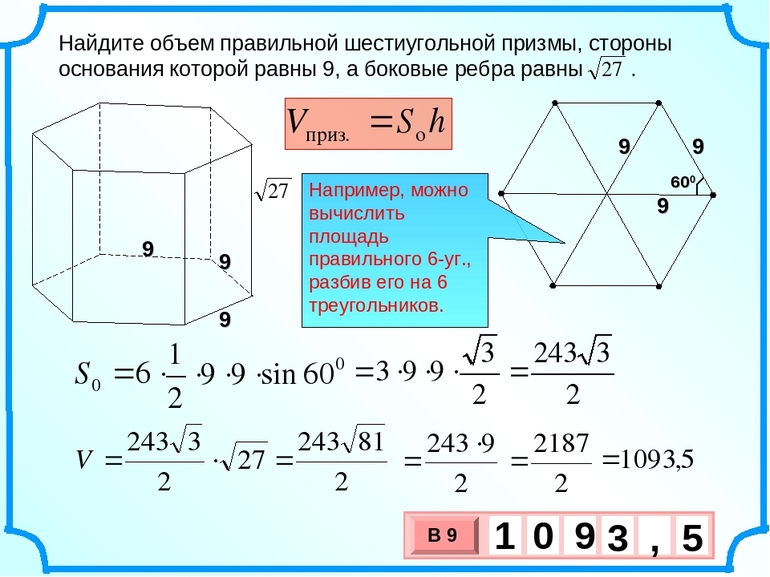
Площадь основания. Так как в основе тела лежат правильные шестиугольники, то, используя их свойства, можно получить формулу: S = (3 * a 2 * √ 3) / 2, где: а — сторона многоугольника.
Площадь полной поверхности. Определяется она из равенства: Sb = 6 * a * h + 2 * (3 * a 2 * √ 3) / 2. Из-за того, что площадь плоскости можно получить путём сложения сторон призмы и двух поверхностей её основания, а грань — прямоугольник (S прямоугольника = a * h), то указанная формула будет верной.
Объём. Он равняется произведению площади основания на высоту. Роль последней может играть ребро любой стороны, например, BB1. Учитывая сказанное, формулу можно записать так: V = S * BB 1 = ((3 √ 3) / 2) * (a 2 * h).

Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .

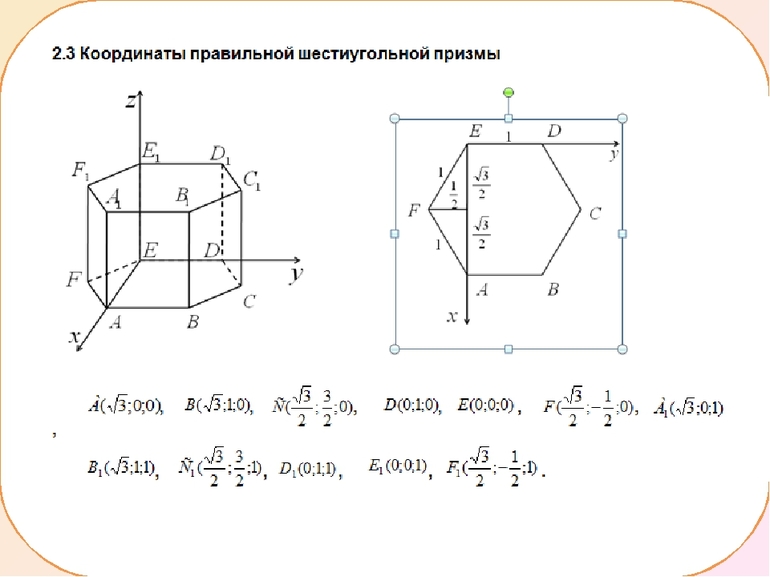
Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.

По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA1 2 + AE 2 )= √(h 2 + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB1 2 + BE 2 ) = √(h 2 + 4 *a) = √5 *a. Сторона FE1 = √(FE 2 + EE 2 ) = √(h 2 + a 2 ) = √2 *a.

Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h 2 + a 2 ), что и следовало доказать.

Решение простого примера

Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.

Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.

Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.

Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.

С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.

Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E 2 = C1C 2 + CE = 2 2 + (4 c3) 2 . C1E 2 = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.

Задача высокого уровня

Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.

Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.

В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.

Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.

Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.

Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R 2 = (12 * 2) / 3 √ 3 = 8 /√3.

Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a 2 * sin60 / 2 = (R 2 * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.

В этой статье приведено несколько примеров пошагового построения сечения правильной шестиугольной призмы методом следов. Иногда к методу следов был взят в помощь аксиоматический метод. Я старалась избегать пользоваться методом внутреннего проецирования намеренно, чтобы показать построение именно методом следов.

Задача 1. Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки .

Шаг 1. Проведем прямую , принадлежащую плоскости сечения. Благодаря тому, что точки и лежат в основании призмы, прямая также принадлежит плоскости основания, а значит, будет пересекаться с другими прямыми, также лежащими в этой плоскости. Тогда можно провести прямую , и определить точку пересечения и – . Точка принадлежит плоскости грани , поскольку прямая принадлежит ей.

Шаг 2. Точки и можно соединить прямой. Прямая пересечет ребро в точке . Проводим прямую в плоскости основания и находим ее пересечение с прямой – точку .

Шаг 3. Через точки и проводим прямую. Она принадлежит плоскости грани , поэтому обязательно пересечется с прямой этой плоскости – в точке . Точка лежит “под” призмой, ниже ее основания. Точка , благодаря принадлежности прямой , также принадлежит и плоскости грани , а в этой плоскости у нас имеется точка – точка .

Шаг 4. Следовательно, можно соединить точки и прямой. Эта прямая пересечет ребро в точке .

Шаг 5. Точка принадлежит прямой , а следовательно, лежит в плоскости грани , таким образом, ее можно соединить с точкой этой же плоскости прямой . Эта прямая пересечет ребро в точке . Для дальнейшего построения нам нужны точки в плоскости верхней грани призмы. Добудем их. Продлим прямую до пересечения с прямой . Отметим точку .

Шаг 6. Проведем прямую , принадлежащую грани , и найдем точку ее пересечения с прямой – точку . Тогда точки и принадлежат плоскости верхней грани (за счет принадлежности прямым этой плоскости) и их можно соединять прямой.

Шаг 7. Находим точки пересечения прямой с ребрами и – точки и .

Шаг 8. Соединяем все полученные точки отрезками.

Окончательный вид сечения:

Задача 2. Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки .

Шаг 1. Проведем прямую . Она принадлежит секущей плоскости. Также проведем проекцию этой прямой на плоскость нижнего основания призмы – прямую . Точка их пересечения одновременно принадлежит секущей плоскости и плоскости нижнего основания призмы. Обозначим ее .

Шаг 2. Аналогично поступим с точками и : проводим прямую и ее проекцию в плоскости нижнего основания. Их пересечение – точка секущей плоскости , одновременно лежащая в нижнем основании.

Шаг 3. Имея две точки в плоскости нижнего основания, проведем через них прямую , точки которой принадлежат секущей плоскости.

Проведем прямую . Она лежит в плоскости основания, но одновременно – в плоскости боковой грани, поэтому ее точки принадлежат этой боковой грани. Точка пересечения прямых и , таким образом, принадлежит плоскости боковой грани призмы и плоскости сечения.

Шаг 4. Проводим прямую в плоскости боковой грани и отыскиваем точку пересечения ею ребра – точку .

Осталось немного: найти точку плоскости сечения на ребре , и пару точек в плоскости основания.

Шаг 5. Проведем прямые и в плоскости основания. Они пересекут прямую секущей плоскости в точках и .

Шаг 6. Точки и принадлежат плоскости грани , проведем через них прямую. Найдем точку, где эта прямая пересечет ребро – точку . Точки и лежат в плоскости грани . Проводим через них прямую и находим точку пересечения этой прямой с ребром – .

Шаг 7. Соединяем точки отрезками.

Окончательный вид построенного сечения:

Окончательный вид построенного сечения

Задача 3. Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки .

Шаг 1. Проводим прямую секущей плоскости, а также ее проекцию в плоскости основания . Прямая принадлежит плоскости основания и пересечет прямую в точке . Заметим, что точка не является точкой секущей плоскости.

Шаг 2. Из точки проводим перпендикуляр к плоскости основания (к прямой ), его пересечение с прямой – точка – принадлежит секущей плоскости, а также плоскости грани .

Шаг 3. Соединим точки и . Прямая пересечет ребро призмы в точке .

Шаг 4. Заполучив точку , можем провести отрезок . Вот тут-то нам и понадобится аксиоматический метод. Так как грань параллельна грани , то плоскость рассечет ее по прямой, которая будет параллельна . Вот и проведем через такую параллельную прямой прямую. Она пересечет ребро в точке .

Шаг 5. Проведем также через точку прямую, параллельную прямой . Это можно сделать, так как грань параллельна грани . Прямая эта пересечет ребро в точке .

Шаг 6. Соединяем точки отрезками.

Задача 3. Окончательный вид

Задача 4. Построить методом следов сечение шестиугольной призмы плоскостью, проходящей через точки .

Шаг 1. Через точки и проводим прямую секущей плоскости. Также проведем проекции этой прямой на верхнее и нижнее основание – на верхнее, и – на нижнее. Точки пересечения прямой с проекциями – это точки прокола данной прямой оснований призмы. Верхнее основание прямая прошьет в точке , а нижнее – в точке . Таким образом, мы заполучили точки секущей плоскости в плоскостях верхнего и нижнего оснований.

Шаг 2. Точки и принадлежат одной плоскости, проводим через них прямую. Эта прямая даст нам две точки: точку , в которой она пересечет ребро , и точку , в которой она пересечет ребро .

Шаг 3. Приобретя точку в грани , проведем прямую . Она пересечет ребро в точке .

Задача 4. Шаги 2-3.

Шаг 4. Проведем через точку в плоскости основания призмы прямую, параллельную прямой (или можно провести через точки и ). Эта прямая пересечет ребро в точке .

Читайте также: