Как сделать полином

Добавил пользователь Алексей Ф.
Обновлено: 05.10.2024

Формулы полиноминальных преобразований используются для перевода исходных координат (обычно локальных-прямоугольных) в конечные (обычно спроектированные - прямоугольные). В зависимости от искажения изображения, количества контрольных точек (GCP – ground control point), и их размещения относительно друг друга, для выражения необходимого преобразования могут потребоваться достаточно сложные полиноминальные формулы. Сложность полинома выражается через его порядок. Порядок – это показатель наивысшей степени, используемой в полиноме.

Линейные преобразования

Преобразование 1-го порядка – линейное преобразование. Это преобразование может изменять:

положение по X и/или Y; Изменение положения, смещает изображение на определенное число пикселей по X и Y.
масштаб по X и/или Y; Коэффициенты масштабирования по X и Y могут быть различными
наклон по X и/или Y;
поворот; При повороте, можно определить любое положительное или отрицательное число градусов, для поворота по- и против часовой стрелки соответственно. Поворот происходит вокруг центрального пикселя изображения.
Отражение; слева направо, сверху вниз, сверху вниз и слева направо (аналогично повороту на 180 градусов)

Преобразование 1-го порядка может быть использовано для перевода исходного (например только что отсканированного) изображения в прямоугольную систему координат, преобразования одной прямоугольной системы координат в другую, обычно это преобразование используется для относительной небольших фрагментов.

Примерами применения этого преобразования могут быть: исправление перекосов в данных дистанционного зондирования, поворота отсканированных топографических листов, и поворота данных с нисходящих орбит так, что бы север был вверху изображения (а не по ходу орбиты).

Преобразование 1-го порядка также может быть использовано для данных, которые уже спроецированы на плоскость. Например, часто данные дистанционного зондирования, уже находятся в локальной прямоугольной системе координат, но не приведены к соответствующей проекции. При использовании данного типа преобразования, не имеет смысла увеличение порядка преобразования, если при первом порядке возникает большая среднеквадратическая ошибка. Сначала, необходимо проверить другие возможные источники ошибок: качество опорных точек, их распределение и другие возможные систематические ошибки.

На рисунке показано, как изменяются данные при линейных преобразованиях.

Для осуществления полиномиального преобразования первой степени необходимо найти 6 коэффициентов - по три на каждую координату (X и Y): a₀, a₁, a₂, b₀, b₁, b₂. Эти коэффициенты, далее используются в собственно уравнениях полиномиального преобразования первой степени (эквивалентного также аффинному преобразованию):

где x,y - исходные координаты, x₀,y₀ - конечные координаты

Нелинейные преобразования

Нелинейные преобразования – это преобразования 2-го и более порядка. Эти преобразования могут корректировать нелинейные искажения. На рисунке изображены примеры результатов некоторых нелинейных преобразований.

Преобразования 2-го порядка могут быть использованы для преобразования данных в географической системе координат (широта, долгота) в прямоугольную, для преобразования данных больших областей (для учета кривизны Земли), для точно привязки искаженных по той или иной причине данных (например, из-за искажений линз камеры, плохо отсканированных материалов) и т.д.

Матрица преобразования

Матрица преобразования рассчитывается по контрольным точкам. Матрица состоит из коэффициентов, которые используются в формулах полиномов для преобразования координат. Размерность матрицы зависит от порядка используемого преобразования. Коэффициенты матрицы преобразований рассчитываются таким образом, чтобы получить формулы полиномиального преобразования с как можно меньшей ошибкой перевода исходных координат в конечные. Получить коэффициенты, которые не приводят к ошибкам удается не всегда. Пример, иллюстрирующий ошибку исходной координаты относительно конечной и кривой, аппроксимирующей зависимость между ними, выраженной полиномом (не все точки лежат на линии, расстояние от исходной точки до кривой полинома - среднеквадратичная ошибка). Для простоты в примере показано только отношение исходной и конечной координаты X и описывающее его кривая, в реальной жизни, исходных координат 2 и конечных координат 2, поэтому зависимость между ними аппроксимируется не кривой, а плоскостью.

Количество коэффициентов матрицы преобразований для преобразования порядка t равно:

Это число необходимо умножить на 2 – для двух наборов коэффициентов, один - для X, другой для Y. Более простая формула для получения количества коэффициентов:

Очевидно, что размерность матрицы преобразований увеличивается с ростом порядка преобразования, соответственно минимальное количество контрольных точек необходимых для вычислений коэффициентов матрицы тоже растет.

Каждая контрольная точка влияет на расчетные коэффициенты, если нет идеального соответствия каждой контрольной точки полиному, который представлен этими коэффициентами. Расстояние между кривой и расчетной координаты точки – называется ошибкой RMS (среднеквадратической ошибкой точки). Для расчета матрицы преобразований по набору контрольных точек используется метод среднеквадратической регрессии (метод наименьших квадратов) на основе контрольных точек расставляемых пользователем от исходного (привязываемого) материала, к конечному материалу (тому, к которому привязывают).

Формула вычисления полинома порядка t

Где: t – порядок полинома, a_k и b_k – коэффициенты, индекс k для a_k и b_k вычисляется как:

Например, для преобразования 3-го порядка будет использоваться 20 коэффициентов:

Формула для преобразования 3-го порядка, после вычисления коэффициентов, может выглядеть так:

Влияние порядка преобразования

Расчет формул полиномов высоких порядков и выходных значений сложнее, чем расчет полиномов первых порядков. Поэтому, полиномы высоких порядков применяются для изображений требующих для привязки более сложных искажений. Для понимания влияния различных порядков преобразования при спрямлении изображения, полезно рассмотреть выходные величины полиномов различных порядков.

В следующем примере, для просты, используется только одна координата (X), вместо двух (X, Y), которые для расчетов в полиномиальных преобразованиях. Это позволяет использовать двухмерные графики, иллюстрирующие, как использование преобразования определенного порядка позволяет связать исходные и конечные координаты. Из-за того, что в примере используется только координата X, число используемых контрольных точек меньше реально требуемого для преобразований соответствующих порядков.

Коэффициенты, подобные тем, которые использованы в примере, обычно рассчитываются по методу наименьших квадратов. Предположим, что введены следующие контрольные точки:

Что такое многочлены? Познакомимся с этим понятием из курса математики 7 класс. Мы с вами дадим определение многочленам, рассмотрим какие выражения можно назвать многочленами, а какие нельзя. Разберем что такое многочлен стандартного вида и степень многочлена и решим несколько примеров на определение степени многочлена и приведение подобных слагаемых.

Определение многочлена

Многочленом называют алгебраическую сумму одночленов. То есть многочлен — это алгебраическое выражение, которое записывается в виде суммы одночленов.

Пример многочлена: .

Неправильно

Как отличить многочлен от не многочлена — обратите внимание на варианты неправильного называния не многочлена многочленом:

Виды многочленов

Среди многочленов выделяют следующие виды многочлены:

Многочлен состоящий из одного одночлена называется одночленом.
Многочлен, состоящий из двух одночленов, называется двучленом или биномом.
Многочлен, состоящий из трех одночленов, называется трехчленом.

Это стандартные называния таких многочленов, многочлен, состоящий из любого произвольного числа одночленов, большего трех, называется просто многочленом.

Стандартный вид многочлена

Если все входящие в многочлен одночлены имеют стандартный вид и в многочлене приведены подобные слагаемые, то такой многочлен называется многочленом стандартного вида.

Приведем пример: выражение является многочленом стандартного вида.

Степень многочлена

Чтобы определить степень многочлена нужно найти одночлен с наибольшей степенью, входящий в его состав. Например, в многочлене наибольшая степень у одночлена , у которого степень 5. Таким образом, и многочлен будет пятой степени.

Сложение подобных слагаемых

Сумму подобных членов многочлена можно заменить одним членом, если сложить их числовые коэффициенты и оставить буквенную часть. Такое сложение или, иначе, тождественное преобразование, называют приведением подобных слагаемых.

Приведем пример: в многочлене можно сложить подобные слагаемые и , тогда мы получим: и .

Примеры решения задач

Задание 1

Определите степень многочлена .

Решение: наибольшая степень у одночлена , значит, степень многочлена — 3.

Задание 2

Ответ: .

Задание 3

Приведите подобные члены многочлена:

Ответ: .

Задание 4

Приведите подобные члены многочлена:

Ответ: .

Задание 5

Приведите подобные члены многочлена:

Решение: .

Ответ:

Задание 6

Приведите подобные члены многочлена:

Решение: .

Ответ: .

Задание 7

Приведите подобные члены многочлена: .

Решение: .

Ответ: .

Задание 8

Приведите подобные члены многочлена: .

Решение: .

Стоило только разобраться с одночленами, как неугомонная алгебра принесла нам новое испытание. Многочлены — кто они такие, стоит ли их опасаться и что предпринимать при встрече с ними лицом к лицу в 7 классе.

О чем эта статья:

Определение многочлена

Одночлен — это произведение, состоящее из числового множителя и одной или нескольких переменных, каждая из которых взята в неотрицательной степени.

Рассмотрим примеры многочленов:

Если многочлен состоит из двух одночленов, его называют двучленом:

10x − 3x 2
10x — одночлен
−3x 2 — одночлен

Этот же многочлен можно записать вот так:

Это значит, что каждый одночлен важно рассматривать вместе со знаком, который перед ним стоит.

Многочлен вида 10x − 3x 2 + 7 называется трехчленом.

Линейный двучлен — это многочлен первой степени: ax + b. a и b здесь — некоторые числа, x — переменная.

Если разделить многочлен с переменной x на линейный двучлен x − b (где b — некоторое положительное или отрицательное число) — остаток будет только многочленом нулевой степени. То есть некоторым числом N, которое можно определить без поиска частного.

Если многочлен содержит обычное число — это число является свободным членом многочлена.

Например, в многочлене 6a + 2b − x + 2 число 2 — свободный член.

Свободный член многочлена не имеет буквенной части. Кроме того, любое числовое выражение — это многочлен. Например, вот такие числовые выражения — тоже многочлены:

Такие выражения состоят из свободных членов.

Коэффициенты многочлена

Коэффициенты членов многочлена — это числа, которые указаны перед переменными множителями. Если перед переменной нет числа, то коэффициент этого члена = 1.

Иными словами — коэффициенты членов многочлена — это члены многочлена, представленные в виде стандартных одночленов.

Например:

Дан многочлен 2x + 5x − 18y

Все одночлены имеют стандартный вид. 2, 5 и 18 — коэффициенты членов данного многочлена.

Многочлен стандартного вида

Недостаточно просто знать, что такое многочлен и что такое одночлен. Это целая алгебраическая экосистема, где у всего есть названия, определения и особенности.

Давайте разберемся, что такое многочлен стандартного вида. Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.

Получается, что всякий многочлен можно привести к стандартному виду. Таким образом можно получить многочлен, работать с которым гораздо проще и приятнее.

К стандартному виду многочлен приводится очень просто. Нужно лишь привести в нем подобные слагаемые.

Подобные слагаемые — это подобные члены многочлена. Приведение подобных слагаемых в многочлене — приведение его подобных членов. Тут же возникает резонный вопрос: Что такое подобные члены многочлена? Это члены с одинаковой буквенной частью.

Дан красавец многочлен: 3x + 5xy 2 + x − xy 2

Приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

3x и x — подобные слагаемые.
5xy 2 и −xy 2 — подобные слагаемые.

Получаем многочлен вот такого вида: 3x + 5xy 2 + x − xy 2 = 4x + 4xy 2 .

Как видите, в получившемся многочлене нет подобных членов. Такой многочлен — это многочлен стандартного вида.

Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.

Степень многочлена

Многочлен может иметь степень — имеет на это полное право.

Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов.

Из определения можно сделать вывод, что степень многочлена возможно определить только после приведения его к стандартному виду.

Приводим многочлен к стандартному виду.
Выбираем одночлен с наибольшей степенью.

Рассмотрим на примере:

Дан многочлен 6x + 4xy 2 + x + xy 2

Сначала приводим многочлен к стандартному виду — для этого приводим подобные слагаемые:

6x и x — подобные слагаемые
4xy 2 и xy 2 — подобные слагаемые

Получаем многочлен стандартного вида 6x + 4xy 2 + x + xy 2 = 7x + 5xy 2 .

Степень первого одночлена (7x) — 1.
Степень второго одночлена (5xy 2 ) — 3.
Наибольшая из двух степеней — 3.

Отсюда делаем вывод, что многочлен 7x + 5xy 2 — многочлен третьей степени.

Кроме того, можно сделать вывод, что и исходный многочлен 6x + 4xy 2 + x + xy 2 — многочлен третьей степени, поскольку оба многочлена равны друг другу.

В некоторых случаях необходимо сначала привести к стандартному виду одночлены многочлена, а затем уже и сам многочлен.

Пример:

Дан многочлен 6xx 2 + 5xx 2 − 3xx 3 − 3x 2 x

Приведем его к стандартному виду: 6xx 3 + 5xx 2 − 3xx 3 − 3x 2 x = 6x 4 + 5x 3 − 3x 4 − 3x 3

Получившийся многочлен без труда приводим к стандартному виду. Приводим подобные слагаемые:

5x 3 и −3x 3 — подобные слагаемые.
6x 4 и −3x 4 — подобные слагаемые.
6x 4 + 3x 3 − 3x 4 − 3x 3 = 3x 4 − 2x 3
6xx 3 + 5xx 2 − 3xx 3 − 3x 2 x — многочлен четвертой степени.

Практика

Кажется, со стандартным видом многочлена все понятно. Чтобы без труда приводить любой многочлен к стандартному виду, нужно потренироваться, ведь в 7 классе только и разговоров, что о многочленах. Давайте разберем несколько примеров. Попробуйте решить их самостоятельно, сверяясь с ответами.

Задание раз. Приведите многочлен к стандартному виду и определите его степень: 4x + 6xy 2 + x − xy 2 .

Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

4x и x — подобные слагаемые.
6xy 2 и −xy 2 — подобные слагаемые.

Получаем многочлен стандартного вида: 4x + 6xy 2 + x − xy 2 = 5x + 5xy 2 .

Ответ: стандартный вид многочлена 5x + 5xy 2 . Данный многочлен — многочлен второй степени.

Задание два. Приведите многочлен к стандартному виду: 2x 2 y 3 − xy 3 − x 4 − x 2 y 3 + xy 3 + 2x 4 .

Как решаем: сначала необходимо привести все одночлены к стандартному виду: 2x 2 y 3 − xy 3 − x 4 − x 2 y 3 + xy 3 + 2x 4 = (−x 4 + 2x 4 ) + (2x 2 y 3 − x 2 y 3 ) + (− xy 3 + xy 3 ) = x 4 + x 2 y 3 + 0 = x 4 + x 2 y 3 .

Многочлен приведен к стандартному виду.

Ответ: x 4 + x 2 y 3

Задание три. Приведите многочлен к стандартному виду и определите его степень: 8x + 8xy 2 − x + xy 2 .

Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

8x и −x — подобные слагаемые.
8xy 2 и xy 2 — подобные слагаемые.

Получаем многочлен стандартного вида: 8x + 8xy 2 − x + xy 2 = 7x + 9xy 2 .

Ответ: стандартный вид многочлена 7x + 9xy 2 , данный многочлен — многочлен третьей степени.

Разобраться в многочленах не так-то просто. В этой теме немало нюансов и подводных камней. Чтобы не запутаться в множестве похожих одно на другое определений, побольше практикуйтесь. Чтобы перейти на следующую ступень и начать выполнение арифметических действий с многочленами, важно научиться приводить многочлен к стандартному виду.

Excel для Microsoft 365 Word для Microsoft 365 Outlook для Microsoft 365 PowerPoint для Microsoft 365 Excel для Microsoft 365 для Mac Word для Microsoft 365 для Mac PowerPoint для Microsoft 365 для Mac Excel 2021 Word 2021 Outlook 2021 PowerPoint 2021 Excel 2021 for Mac Word 2021 for Mac PowerPoint 2021 for Mac Excel 2019 Word 2019 Outlook 2019 PowerPoint 2019 Excel 2019 для Mac Word 2019 для Mac PowerPoint 2019 для Mac Excel 2016 Word 2016 Outlook 2016 PowerPoint 2016 Excel 2016 для Mac Word 2016 для Mac PowerPoint 2016 для Mac Excel 2013 Word 2013 Outlook 2013 PowerPoint 2013 Excel 2010 Word 2010 Outlook 2010 PowerPoint 2010 Excel 2007 Excel для Mac 2011 Word для Mac 2011 PowerPoint для Mac 2011 Excel Starter 2010 Больше. Основные параметры

В этой теме описывается, какие параметры линии тренда доступны в Office.

Используйте линию тренда этого типа для создания прямой линии, которая наилучшим образом описывает простой линейный набор данных. Она применяется в случаях, когда точки данных расположены близко к прямой. Иначе говоря, прямая линия тренда хорошо подходит для величины, которая возрастает или убывает с постоянной скоростью.

Для расчета точек методом наименьших квадратов прямая линия тренда использует следующее уравнение:

где m — это наклон, а b — смещение.

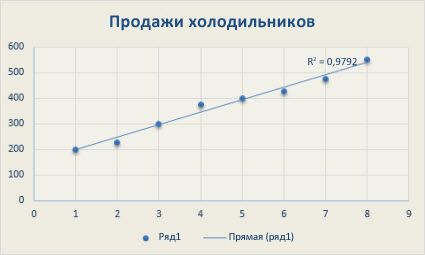
Следующая прямая линия тренда отображает стабильный рост продаж холодильников на протяжении 8 лет. Обратите внимание, что величина достоверности аппроксимации (число от 0 до 1, отображающее степень соответствия ожидаемых значений для линии тренда фактическим данным) равна 0,9792, что свидетельствует о хорошем совпадении расчетной линии с данными.

Отображая оптимизированную кривую, эта линия тренда полезна для описания величины, которая вначале быстро растет или убывает, а затем постепенно стабилизируется. Логарифмическая линия тренда может использовать отрицательные и положительные значения данных.

Для расчета точек методом наименьших квадратов логарифмическая линия тренда использует следующее уравнение:

где c и b — константы и ln — функция натурального логарифма.

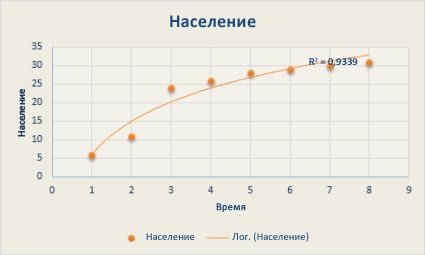
Следующая логарифмическая линия тренда отображает прогнозируемый рост численности населения животных в области с фиксированным пространством, где численность населения была выровнена в результате уменьшения пространства для животных. Обратите внимание, что величина квадрата составляет 0,933, что относительно хорошо подходит для данных.

Эта линия тренда полезна для описания величин, попеременно возрастающих и убывающих. Например, при анализе большого набора данных о нестабильной величине. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Обычно полином второй степени имеет только один экстремум, полином третьей степени — один или два экстремума, а полином четвертой степени — до трех экстремумов.

Для расчета точек методом наименьших квадратов полиномиальная (или криволинейная) линия тренда использует следующее уравнение:

где b и являются константами.

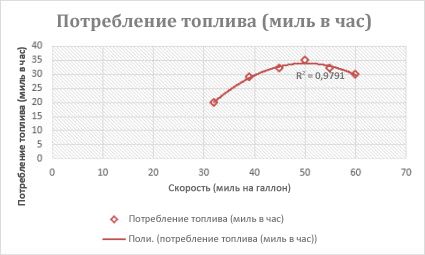
Приведенная ниже полиномиальная линия тренда второй степени (один максимум) отображает зависимость расхода топлива от скорости движения. Близкая к единице величина достоверности аппроксимации (0,979) свидетельствует о хорошем совпадении кривой с данными.

Отображая кривую, эта линия тренда полезна для отображения зависимости, которая содержится в данных, и характеризуется постоянной скоростью роста. Примером такой зависимости может служить ускорение гоночного автомобиля за каждый интервал времени, равный одной секунде. Если в данных имеются нулевые или отрицательные значения, использование степенной линии тренда невозможно.

Для расчета точек методом наименьших квадратов степенная линия тренда использует следующее уравнение:

где c и b — константы.

Примечание: При наличии нулевых или отрицательных значений данных этот параметр недоступен.

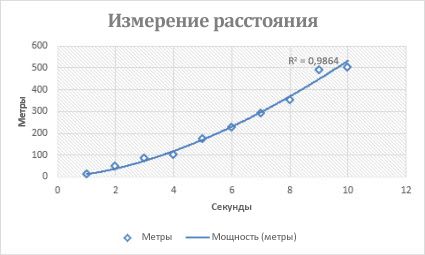
Приведенная ниже диаграмма измерения расстояний отображает зависимость пройденного расстояния от времени. Расстояние выражено в метрах, время — в секундах. Эти данные точно описываются степенной линией тренда, о чем свидетельствует величина достоверности аппроксимации, равная 0,986.

Отображая кривую, эта линия тренда полезна, если скорость изменения данных непрерывно возрастает. Однако для данных, которые содержат нулевые или отрицательные значения, экспоненциальная линия тренда неприменима.

Для расчета точек методом наименьших квадратов экспоненциальная линия тренда использует следующее уравнение:

где c и b — константы и e — основание натурального логарифма.

Приведенная ниже экспоненциальная линия тренда отображает содержание радиоактивного углерода-14 в зависимости от возраста органического объекта. Величина достоверности аппроксимации равна 0,990, что означает очень хорошее соответствие кривой данным.

Эта линия тренда позволяет сгладить колебания данных и таким образом более наглядно отображает характер зависимости. Линейный фильтр строится по определенному числу точек данных (задается параметром Точки). Элементы данных усредняются, и полученный результат используется в качестве точки линии тренда. Так, если параметр Точки равен 2, первая точка линии тренда с линейной фильтрацией определяется как среднее значение первых двух элементов данных, вторая точка — как среднее второго и третьего элементов, и так далее.

Линия тренда с линейной фильтрацией использует такое уравнение:

Число точек в линии тренда с скользящее среднее равно общему числу точек ряда за вычетом числа, указанного для параметра "Точки".

В точечной диаграмме линия тренда базируется на порядке расположения значений X в диаграмме. Для получения оптимального результата перед добавлением линейной фильтрации отсортируйте значения X.

Приведенная ниже линия тренда с линейной фильтрацией отображает тенденцию числа продаж домов на протяжении 26 недель.

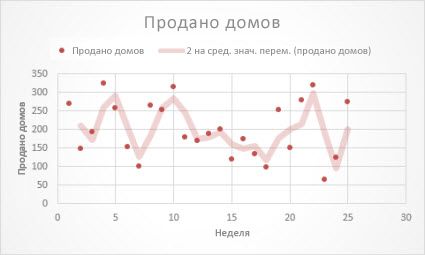
Важно: Начиная с Excel 2005 г., Excel скорректировал способ вычисления значения R2 для линейных линий тренда на диаграммах, где для перехватить линию тренда установлено значение 0 (0). Эта корректировка исправлять вычисления, которые дают неправильные значения R 2, и выравнивает вычисление R 2 с функцией LINEST. В результате на диаграммах, созданных в предыдущих версиях Excel, могут отображаться разные значения R2. Дополнительные сведения см. в таблице Изменения внутренних вычислений линейных линий тренда на диаграмме.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Полином, или многочлен - одна из базовых алгебраических структур, которая встречается в школьной и высшей математике. Изучение полинома - важнейшая тема в курсе алгебры, поскольку с одной стороны многочлены достаточно просты по сравнению с другими типами функций, с другой - широко применяются в решении задач математического анализа. Итак, что такое полином?

Определение

Определение термину полином можно дать через понятие монома, или одночлена.

Мономом называют выражение вида сх₁ i1 x₂ i2 . x_n in . Здесь с - константа, x₁, x₂, . x_n - переменные, i1, i2, . in - показатели степеней переменных. Тогда полином - любая конечная сумма мономов.

Чтобы понять, что такое полином, можно посмотреть на конкретные примеры.

Многочлен с двумя переменными может выглядеть так: х 2 -ху+у 2 . Такой полином называют еще неполным квадратом разности х и у.

Классификации полиномов

По степени полинома

Для каждого монома в составе многочлена находят сумму показателей степени i1+i2+. +in. Наибольшую из сумм называют показателем степени полинома, а одночлен, соответствующий этой сумме, - старшим членом.

Кстати, любую константу можно считать многочленом степени ноль.

Приведенные и неприведенные полиномы

Если у старшего члена коэффициент с равен 1, то многочлен приведен, иначе - нет.

Например, выражение х 2 +2х+1 - приведенный полином, а 2х 2 +2х+1 - неприведенный.

Однородные и неоднородные полиномы

Если степени всех членов полинома равны, то говорят, что такой полином однороден. Все остальные полиномы считаются неоднородными.

Однородные многочлены: х 2 -ху+у 2 , xyz+х 3 +у 3 . Неоднородные: х+1, х 2 +у.

Существуют специальные названия для полинома из двух и трех членов: бином и трехчлен соответственно.

В отдельную категорию выделяют многочлены одной переменной.

Применение полинома одной переменной

Многочлены одной переменной хорошо приближают непрерывные функции различной сложности от одного аргумента.

Дело в том, что такие полиномы можно рассматривать как частичные суммы степенного ряда, а непрерывную функцию можно представить в виде ряда со сколь угодно малой погрешностью. Ряды разложения функции называют рядами Тейлора, а их частичные суммы в виде полиномов - многочленами Тейлора.

Изучить графически поведение функции, аппроксимировав ее некоторым многочленом, зачастую легче, чем исследовать ту же функцию непосредственно или с помощью ряда.

Легко искать производные многочленов. Для нахождения корней у полиномов 4-й степени и ниже существуют готовые формулы, а для работы с более высокими степенями используются приближенные алгоритмы высокой точности.

Существует и обобщение описанных многочленов для функций многих переменных.

Бином Ньютона

Знаменитыми полиномами являются полиномы Ньютона, выведенные ученым для нахождения коэффициентов выражения (х+у) n .

Достаточно посмотреть на несколько первых степеней разложения бинома, чтобы убедиться в нетривиальности формулы:

(х+у) 2 =х 2 +2ху+у 2 ;
(х+у) 3 =х 3 +3х 2 у+3ху 2 +у 3 ;
(х+у) 4 =х 4 +4х 3 у+6х 2 у 2 +4ху 3 +у 4 ;
(х+у) 5 =х 5 +5х 4 у+10х 3 у 2 +10х 2 у 3 +5ху 4 +у 5 .

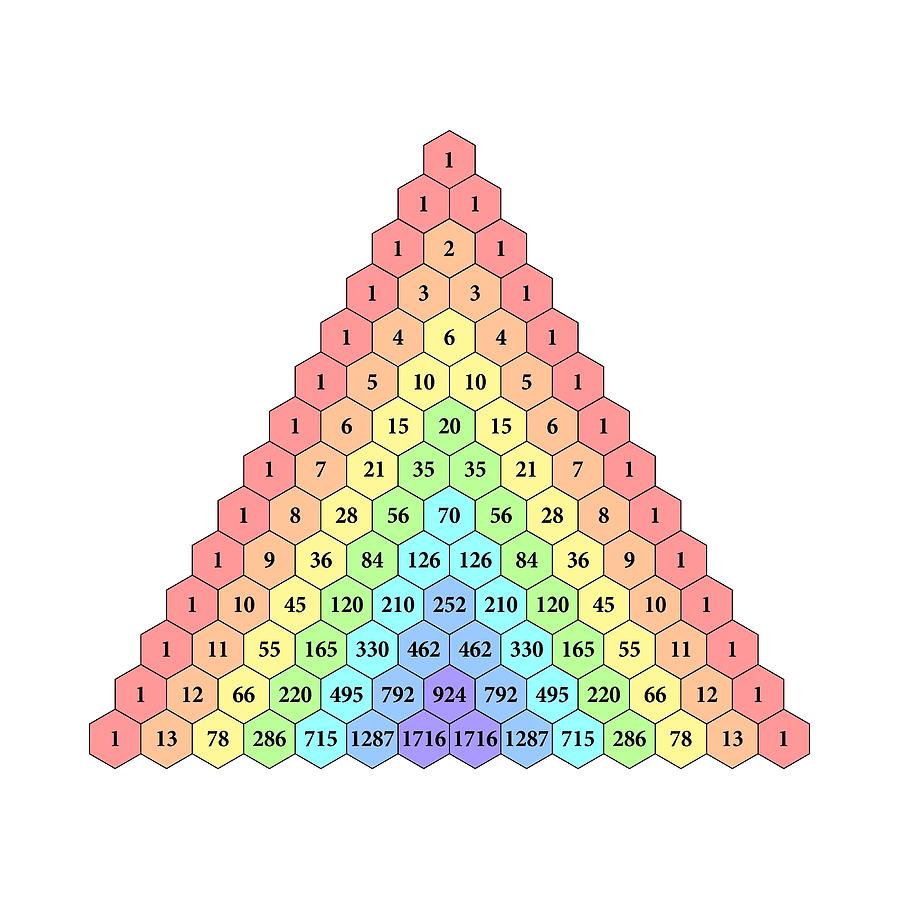
Для каждого коэффициента существует выражение, позволяющее его вычислить. Однако запоминать громоздкие формулы и каждый раз производить необходимые арифметические операции было бы крайне неудобно для тех математиков, которым часто требуются подобные разложения. Им значительно облегчил жизнь треугольник Паскаля.

Фигура строится по следующему принципу. В вершине треугольника пишется 1, а в каждой следующей строке становится на одну цифру больше, по краям ставят 1, а середина строчки заполняется суммами двух соседних чисел из предыдущей.

При взгляде на иллюстрацию все становится понятно.

Разумеется, приведенными примерами, наиболее широко известными, применение многочленов в математике не ограничивается.

Читайте также: