Как сделать логическое высказывание обратное данному

Обновлено: 05.07.2024

Процессор компьютера выполняет арифметические и логические операции над двоичными кодами.

Для того чтобы иметь представление об устройстве компьютера, необходимо познакомиться не только с арифметическими, но и с основными логическими элементами, лежащими в основе его построения.

Для понимания принципа работы таких элементов рассмотрим основные понятия алгебры логики.

Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.

Аналогию между алгеброй и логикой положил в основу своего логического учения основоположник алгебры логики английский математик и логик Дж. Буль (1815–1864).

Логическое высказывание — любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно — 1 или ложно — 0.

Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения.

Истинность или ложность высказываний зависит от истинности и ложности исходных (простых) высказываний и смысла логических операций над высказываниями (пример 26.1). Таким образом, определение истинности некоторого логического выражения — это определение значения некоторой логической функции.

Логическая функция — функция, принимающая значения 0 или 1 в результате логических операций над логическими переменными.

Способы задания логической функции:

1) словесное описание;

2) таблица истинности;

3) формула, записанная с помощью букв, знаков логических операций и скобок;

4) комбинационная схема, составленная из логических элементов;

5) координатный способ (карта Карно);

6) диаграмма Венна (Эйлера).

Области применения алгебры логики:

1) в качестве средства алгоритмического описания в языках программирования для определения логических условий;

2) для формирования логических высказываний в математической логике, лингвистике, теории искусственного интеллекта;

3) в разработке и описании дискретных технических систем;

4) при анализе и синтезе логических устройств.

Карта Карно — таблица, построенная так, что в ее соседние клетки попадают смежные наборы переменных функций — наборы, отличающиеся значением одной переменной (в один набор эта переменная входит в прямой форме, а в другой — в обратной).

Карты Карно были предложены в 1952 г. Эдвардом В. Вейчем (американским ученым в области кибернетики) и усовершенствованы в 1953 г. Морисом Карно, чтобы упростить проектирование цифровых систем.

Морис Карно — американский физик

Пример 26.2. Способы задания логической функции.

1. Функция двух переменных принимает значение 1, если эти переменные равны 1, а во всех других случаях функция равна 0.

A & B

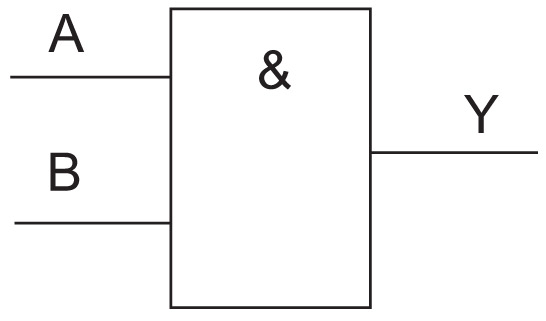
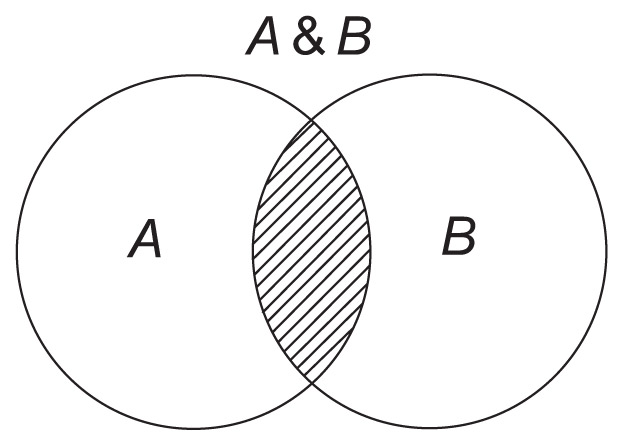
Синтез логических устройств — обратная задача: создание технического устройства на основе математического описания средствами алгебры логики.

В компьютерных устройствах применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае ток проходит, во втором — нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах.

26.2. Логические операции

Рассмотрим основные логические операции — варианты обозначения (пример 26.3), таблицы истинности и логические элементы для каждой из логических операций (примеры 26.4 — 26.9).

Логическое отрицание, или инверсия (лат. inversion — переворачивание), — логическая операция, которая меняет значение исходного высказывания на противоположное.

Инверсия — унарная логическая операция, т. к. выполняется относительно одного высказывания (пример 26.4).

Логические операции, которые выполняются относительно как минимум двух высказываний, называются бинарными. Рассмотрим основные из них.

Логическое умножение, или конъюнкция (лат. conjunctio — соединение), — операция, соединяющая два или более высказываний при помощи логической связки ИЛИ. Результат операции может быть истинным только в том случае, если одновременно истинны исходные высказывания (пример 26.5).

Логическое сложение, или дизъюнкция (лат. disjunction — разделение), — операция, соединяющая два или более высказываний при помощи логической связки ИЛИ. Результат операции будет истинным, если истинно хотя бы одно из исходных высказываний (пример 26.6).

Тот, кто хочет подробно разбираться в цифровых технологиях должен понимать основы такой темы, как алгебра логики. В этой статье будут разобраны основные определения, а также показаны самые важные логические операции, такие как конъюнкция, дизъюнкция, импликация и т.д.

Основные положения

Для начала следует разобраться, для чего нужна алгебра логики – главным образом, этот раздел математики и информатики, нужен для работы с логическими выражениями и высказываниями.

Логическим высказыванием называется утверждение (или запись), которое мы можем однозначно классифицировать, как истинное или ложное (1 или 0 в информатике).

Примером таким высказываний будут являться:

Сегодня светит солнце;
5 > 3;
Химическая таблица элементов была разработана Д.И. Менделеевым.

Отсюда можно сделать вывод, что в русском языке логическими высказываниями являются повествовательные предложения, однако далеко не все повествовательные предложения являются логическими высказываниями . Пример: химия скучный предмет. Здесь мы не можем однозначно установить ложно ли это выражение или истинно.

Логические высказывания делятся на два типа — простые и сложные.

Простые высказывания состоят из одного утверждения, которые мы можем однозначно охарактеризовать, как истинные или ложные.
Сложные же состоят из нескольких таких утверждений, которые объединены с помощью логических операций (рассмотрены дальше).

В алгебре логики, как простые, так и сложные высказываниями описываются булевыми выражениями.

Булево выражение – это символическое (знаковое) описание высказывания.

В таких выражениях простые высказывания выступают в роли переменных и обозначаются буквами латинского алфавита, а операции обозначаются при помощи специальных знаков . После выполнения всех операций и упрощения выражения мы получаем результат, на основании которого строится таблица истинности.

Операции

Ниже рассмотрим основные операции, которые применяются в булевой алгебре. Их хватит, чтобы упростить львиную долю всех выражений, которые Вам встретятся.

Конъюнкция

Функция может работать как с двумя операндами (высказываниями), так и с тремя, четырьмя и т.д. В математике обозначается с помощью знаков \( \wedge \) и &. Обозначение в языках программирования AND, &&. Таблица истинности для двух операндов:

Дизъюнкция

Булево сложение, также как и умножение, может работать с произвольным количеством операндов. В математике обозначается как V, а в программировании с помощью OR или I.

Инверсия

Логическое отрицание – функция, работающая с одним высказыванием, и заменяющая истину на ложь, а ложь на истину. В математике обозначается с помощью черты над значением, а в программирование и информатике с помощью слова NOT.

Импликация

Результирующее значение будет ложным только тогда, когда из истинного высказывания будет следовать ложное следствие . Имеет обозначение в виде стрелочки \( \Longrightarrow \) . Важно: импликация работает только с двумя операндами.

Эквивалентность

Обозначается с помощью трех черточек или ⟺.

Порядок выполнения операций

Логические операции выполняются в следующем порядке:

Первой выполняется инверсия переменных.
Вторым выполняется конъюнкция (булево умножение);
Третьим номером идет дизъюнкция (сложение);
Затем выполняется импликация;
Самым низким приоритетом выполнения обладает эквивалентность.

Если в формуле указаны скобки, то порядок выполнения действий в скобках точно такой же, как написано выше.

Пример

Дано два отрезка B = [2,10], C = [6,14]. Из предложенных вариантов ответа выберите такой отрезок A, что формула \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) истинна при любом значении z. Варианты ответа:

Решение: Подставим в уравнение \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) =1 значения B и C и составим таблицу истинности:

Получившаяся формула \( ((z \in A) \Longrightarrow (z \in [2,10])) \vee (z \in [6,14])=1 \). По условию \( z \in A \)=1.

Таблица истинности для всех отрезков:

Ответ: A = [3,11].

Видео

Заключение

Вот Вы и познакомились с основными логическими операциями и понятиями и знаете, что такое булево сложение и умножение. Если вас заинтересовала данная тема, то можете изучить булевы законы. Эти законы не проходятся в рамках школьной программы и служат для упрощения сложных выражений.

Математическая логика — это раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.

Алгебра высказываний

Логические операции

Операции над высказываниями задают в виде таблиц, называемых таблицами истинности.

Отрицание высказывания

Конъюнкция высказываний

Дизъюнкция высказываний

В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.

Импликация высказываний

Эквивалентность высказываний

Если в выражении присутствуют арифметические операции, операции сравнения и логические операции, то порядок старшинства операций следующий:

• сначала выполняются арифметические операции (порядок старшинства арифметических операций: первыми выполняются все операции умножения и деления, потом операции сложения и вычитания);
• затем — операции и операции сравнения (в том порядке, в каком они встречаются в выражении):
• наконец, логические операции, причем первой везде выполняется операция отрицания, затем конъюнкции, потом дизъюнкции и т. д.

Использование различных операций позволяет в удобной аналитической форме задавать различные множества.

Например, множество точек А, заштрихованное на рис. 1.16, может быть задано следующей формулой:

Система операций называется полной, если всякая формула эквивалентна некоторой формуле, в которую входят только операции из системы . Система введенных пяти операций (отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности) полная, хотя вообще говоря, избыточна, так как одни логические операции могут быть выражены через другие. Например, импликация и эквивалентность можно выразить через отрицание, конъюнкцию и дизъюнкцию следующим образом:

Булевы функции

выражает функцию от переменных А, В и С.

Наиболее важные тождественно истинные формулы получили название Основные законы математической логики.

Основные законы математической логики

1.Коммутативность

2.Ассоциативность

3.Дистрибутивность

4.Законы де Моргана

5.Закон поглощения

6.Закон идемпотентности

8.Закон противоречия

9.Закон исключения третьего

10.Закон двойного отрицания

Пример:

Упростить выражение, используя тождественны преобразования

Существует бесконечное множество тавтологий. Некоторы из них легли в основу методов доказательства.

Основные методы доказательств

При построении любой теории выделяется некоторый набор высказываний, так называемых аксиом, истинность которых постулируется. Из аксиом чисто логическим путем может был установлена истинность некоторых других высказываний называемых теоремами. Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством. Высказывание, которое можно доказать, называется теоремой.

Формально каждая теорема может быть выражена в форме импликации где посылка А называется условием теоремы, а следствие В — заключением. Теорема верна, если выражающая ее импликация тождественно истинна, т. е. является тавтологией. Тавтологии рассматривают как некоторые логически истинные схемы рассуждений. В этой связи тавтологии играют роль законов, определяющих построение правильных умозаключений. Существует бесконечное множество тавтологий. Некоторые из них легли в основу методов доказательства. Основные методы доказательств.

Метод цепочек импликаций

Метод цепочек импликаций состоит в том, что из посылки А страивается цепочка из -импликаций, последним высказыванием в которой является заключение теоремы В, т. е.

В основе этого метода лежит закон цепного высказывания или закон силлогизма

Метод от противного

Метод необходимого и достаточного

а) доказывается, что если имеет место А, то справедливо В (В необходимо для А);

б) если имеет место В, то имеет место и А (В достаточно для А).

Доказательство таким методом базируется на законе тавтологии:

Алгебра предикатов

Предикатом заданным на множествах

Рассмотрим примеры, одноместный предикат на множестве комплексных чисел, при этом, например, если истинное высказывание, а

Логические операции над предикатами

Отрицание предиката

Пусть предикат задан на множествах Предикат называется отрицанием предиката тогда и только тогда, если при одних и тех же кортежах высказывание истинно, когда ложно и наоборот. Обозначение

Конъюнкция предикатов

Пусть на множествах заданы два — местных предиката и . Конъюнкцией этих предикатов называется предикат

который истинен для одних и тех же кортежей только тогда, когда оба предиката — и и истинны.

Дизъюнкция предикатов

Импликация предикатов

Эквивалентность предикатов

Квантор существования

Квантор существования есть операция, которая предикат превращает в высказывание: «существует хотя бы один

Кванторы обладают свойствами, являющимися аналогами законов де Моргана:

Переход от или называется квантификацией или связыванием переменной . Связанная переменная фактически не является переменной, т. е. переход от или от не меняет истинности выражений. Навешивание переменной на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных

Связывая обе переменные данного предиката, получим высказывания:

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Логическая операция инверсия — унарная операция над высказываниями, в результате выполнения которой высказывание становится противоположным исходному высказыванию.

Другие названия отрицания — отрицание или логическое НЕ.

Инверсия или отрицание изучается в информатике при рассмотрении раздела алгебра логики.

В естественных языках отрицанию соответствует частица ‘не‘ или слова ‘неверно, что‘. Например, если высказывание A = ‘Москва — столица России’, то его отрицание будет звучать как ‘Москва не столица России’.

В языках программирования для отрицания используют обозначение ‘ not ‘ или восклицательный знак ‘ ! ‘ (например, not(x = 5) или !(x ).

Для обозначения отрицания используют символ ¬ или черту над высказыванием. Например, отрицание A можно обозначить либо ¬A , либо \overline.

Как набрать знак инверсии на клавиатуре

В Word чтобы набрать символ ¬ необходимо нажать левый Alt, и удерживая его на цифровой клавиатуре (которая справа клавиатуры) набрать цифры 0172. Т. е. символ ¬ — это Alt+0172 . Режим Num Lock должен быть включен.

Чтобы сделать черту над буквой, необходимо зайти в пункт меню Вставка -> Формула (или Уравнение). После этого на панели инструментов найти диакритические знаки и среди них нужный нам знак с чертой над буквой.

Таблица истинности инверсия

Отрицание и круги Эйлера

Обозначим высказывание A кругом, тогда отрицание A будет располагаться снаружи круга.

Читайте также: