Как сделать конъюнкцию
Обновлено: 07.07.2024
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
| A | ¬A |
| 1 | 0 |
| 0 | 1 |
Высказывание $A↖$ ложно, когда А истинно, и истинно, когда А ложно.
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A↖$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.

Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.

Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.

Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖ ∧B) ∧ (A ∧ B↖)$ |
| Импликация | А → В | $A↖ ∨ B$ |
| Эквивалентность | А ∼ В | $(A↖ ∧ B↖) ∨ (A ∧ B)$ |
Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ∨ (X 3) ∨ (1 3) ∨ (12 3) ∨ (3 2) → (X > 5)) .
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 ≤ a ∨ A ∨ sin(π/a - π/b) a + b ∨ A ∧ B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) b a + a b > a + b, после подстановки получим: 3 2 + 2 3 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (b a + a b > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы $↖ ∧ X2 ∨ ↖ ∨ X1$.
| X1 | X2 | $↖$ | $↖$ \ X2 | X1 ∧ X2 | $↖$ | $↖$ ∧ X2 ∨ $↖$ | $↖$ ∧ X2 ∨ $↖$ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ∧ X2 ∨ X1 ∧ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ∧ X2 ∨ $↖$ ∧ $↖$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ∨ X2 ∧ X1 ∨ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ∨ $↖$ ∧ $↖$ ∨ X2.
Таким образом, получена запись логической функции в КНФ.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ∨ $↖$ ∧ $↖$ ∨ X2 = X1 ∧ $↖$ ∨ X1 ∧ X2 ∨ $↖$ ∧ $↖$ ∨ $↖$ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ $↖$ ∧ $↖$ ∨ 0 = X1 ∧ X2 ∨ $↖$ ∧ $↖$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | $↖$ ∧ X2 |
| 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∨ $↖$ ∧ X2 .
Ее можно упростить: X1 ∧ X2 ∨ $↖$ ∧ X2 = X2 ∧ (X1 ∨ $↖$) = X2 ∧ 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
| X1 | X2 | X3 | F(X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | • | X1 ∧ X2 ∧ X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | • | $↖$ ∧ X2 ∧ X3 |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | • | X1 ∧ X2 ∧ $↖$ |
| 1 | 0 | 0 | 1 | • | X1 ∧ $↖$ ∧ $↖$ |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∧ X ∨ $↖$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $↖$ ∪ X1 ∧ $↖$ ∧ $↖$.
Формула достаточно громоздка, и ее следует упростить:
X1 ∧ X2 ∧ X3 ∨ $↖$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $↖$ ∨ X1 ∧ $↖$ ∧ $↖$ = X2 ∧ X3 ∧ (X1 ∨ $↖$) ∨ X1 ∧ $↖$ ∧ (X2 ∨ $↖$) = X2 ∧ X3 ∨ X1 ∧ $↖$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.

Информатика
Конъюнкция, дизъюнкция эквивалентность, инверсия, импликация — сложные для запоминания и понимания термины логики, науки, которая и сама по себе сложная для освоения. Но при ближайшем рассмотрении все слова оказываются более простыми, но обозначают совершенно не простые понятия. Используются термины не только в логике, но и в информатике. Объясняется это тем, что архитектура компьютера построена на понятиях математической логики.
Логика применима для решения задач по геометрии, физике, теории вероятности, понимания некоторых противоречивых речевых оборотов и сложных для непрофессионала научных текстов. Для понимания терминов и сферы их применимости изучим несколько вспомогательных понятий:
- Высказывание — одностороннее речевое предложение, которое гарантированно выражает одну из позиций — истину или ложь. В математике и информатике истинное высказывание обозначают как единицу (1), а ложное, как ноль (0).
- Логическое выражение — высказывание в сопровождении дополнительных величин, в зависимости от значения которых выражение правильное (1), или неправильное (0).
- Логическая операция — умственное действие по использованию новых понятий, изменению объема или содержания существующих понятий.
- Сложное логическое выражение — несколько простых логических выражений, соединенных путем логических операций.
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Если одно из выражений ложное, то света в комнате не будет.
Дизъюнкция, логическое сложение, которое подчиняется правилам математического сложения. Если одно из слагаемых истина (то есть 1) то результат получается 1 (в математике также возможен результат 2, но в логике обозначаем 1, как истинное выражение). Если оба исходных понятия ложные (0), то и результат не может быть истиной (1). Таблица для дизъюнкции выглядит так:
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
А формула принимает вид: F = A + B.
| А | В |
| 0 | 1 |
| 1 | 0 |
| А | В | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Эквивалентность — операция в логике, при которой истина получается только в том случае, если обе части выражения истинны:
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
В сложном логическом выражении существует определенный порядок выполнения операций:
- Инверсия;
- Конъюнкция;
- Дизъюнкция;
- Импликация;
- Эквивалентность.
Если нужно изменить этот порядок, то используют скобки.
Как написать студенческую работу, чтобы её 100% приняли?
Возникают ситуации, когда очень сложно сделать работу, когда совершенно не понятно каков должен быть конечный результат. В таких случаях лучше не тратить лишние время и нервы, а обращаться к знающим людям.
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
- алгебра логики
- высказывание
- логическая операция
- конъюнкция
- дизъюнкция
- отрицание
- логическое выражение
- таблица истинности
- законы логики
1.3.1. Высказывание
Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами. Многие математические объекты (целые и рациональные числа, многочлены, векторы, множества) вы изучаете в школьном курсе алгебры, где знакомитесь с такими разделами математики, как алгебра чисел, алгебра многочленов, алгебра множеств и т. д.
Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
В русском языке высказывания выражаются повествовательными предложениями. Но не всякое повествовательное предложение является высказыванием.
Побудительные и вопросительные предложения высказываниями не являются.
Высказывания могут строиться с использованием знаков различных формальных языков — математики, физики, химии и т. п.
Примерами высказываний могут служить:
Не являются высказываниями числовые выражения, но из двух числовых выражений можно составить высказывание, соединив их знаками равенства или неравенства. Например:
Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «X
1.3.2. Логические операции
Высказывания бывают простые и сложные. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из простых с помощью логических операций.
Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.

Конъюнкция
Самостоятельно установите истинность или ложность трёх рассмотренных выше высказываний.
Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Для записи конъюнкции используются следующие знаки: И, ?, •, &.
Например: А И В, А ? В, А • В, А&В.
Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:

В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы А и В), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: 00, 01, 10, 11. В последнем столбце записан результат выполнения логической операции для соответствующих операндов.
Конъюнкцию также называют логическим умножением.
Дизъюнкция. Инверсия
Самостоятельно установите истинность или ложность трёх рассмотренных выше высказываний.
Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Для записи дизъюнкции используются следующие знаки: ИЛИ, ?, |, +. Например: А ИЛИ В, A?B, А|В, А+В.
Дизъюнкция определяется следующей таблицей истинности:

Дизъюнкцию также называют логическим сложением. Подумайте почему.
Инверсия
Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Для записи инверсии используются следующие знаки: НЕ, ¬, — . Например: НЕ А, ¬ А,

Инверсия определяется следующей таблицей истинности:

Инверсию также называют логическим отрицанием.
Любое сложное высказывание можно записать в виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки. Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция. Изменить порядок выполнения операций можно с помощью расстановки скобок.
Логические операции при выполнении имеют следующий приоритет: ин версия, конъюнкция, дизъюнкция.
1.3.2. Логические операции
Решение. Изобразим множество всех web-страниц рассматриваемого сектора сети Интернет кругом, внутри которого разместим два круга: одному из них соответствует множество web-страниц, где истинно высказывание А, второму — где истинно высказывание В (рис. 1.3).

Изобразим графически множества web-страниц, для которых истинны выражения и высказывание а) — в) (рис. 1.4).

Построенные схемы помогут нам ответить на вопросы, содержащиеся в задании.
Выражение А ИЛИ В истинно для 7000 web-страниц, а всего страниц 5 000 000. Следовательно, выражение А ИЛИ В ложно для 4 993 000 web-страниц. Иначе говоря, для 4 993 000 web-страниц истинно выражение НЕ (А ИЛИ В).
Выражение A ? В истинно для тех web-страниц, где истинно А (4800), а также тех web-страниц, где истинно В (4500). Если бы все web-страницы были различны, то выражение A ? В было бы истинно для 9300 (4800 + 4500) web-страниц. Но, согласно условию, таких web-страниц всего 7000. Это значит, что на 2300 (9300 — 7000) web-страницах встречаются оба слова одновременно. Следовательно, выражение А & В истинно для 2300 web-страниц.
Самостоятельно запишите логическое выражение, соответствующее рассмотренному выше высказыванию.
1.3.3. Построение таблиц истинности для логических выражений
Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных. Для построения таблицы истинности следует:
- 1) подсчитать n — число переменных в выражении;
- 2) подсчитать общее число логических операций в выражении;
- 3) установить последовательность выполнения логических операций с учётом скобок и приоритетов;
- 4) определить число столбцов в таблице: число переменных + число операций;
- 5) заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в п. 3;
- 6) определить число строк в таблице (не считая шапки таблицы): m = 2 n ;
- 7) выписать наборы входных переменных с учётом того, что они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2 n — 1;
- 8) провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
Построим таблицу истинности для логического выражения A ? А & Б. В нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре столбца:

Наборы входных переменных — это целые числа от 0 до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11.
Заполненная таблица истинности имеет вид:

Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение A ? А & В равносильно логической переменной А.
1.3.4. Свойства логических операций
Рассмотрим основные свойства логических операций, называемых также законами алгебры логики.
1. Переместительный (коммутативный) закон:
2. Сочетательный (ассоциативный) закон:
(A ? B) ? C = A ? (B ? C).
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
3. Распределительный (дистрибутивный) закон:
A ? (В & С) = (A ? В) & (A v С).
4. Закон двойного отрицания:

Двойное отрицание исключает отрицание.
5. Закон исключённого третьего:
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
6. Закон повторения:
7. Законы операций с 0 и 1:
8. Законы общей инверсии:
Законы алгебры логики могут быть доказаны с помощью таблиц истинности.
Докажем распределительный закон для логического сложения:
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Пример 2. Найдём значение логического выражения

Решение. При X = 0 получаем следующее логическое выражение:


Так как логические выражения 0
Элементы алгебры логики. Решение логических задач
Рассмотрим несколько способов решения логических задач.
Задача 1. Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую бабушкину вазу. На вопрос, кто разбил вазу, они дали такие ответы:
- Серёжа: 1) Я не разбивал. 2) Вася не разбивал.
- Вася: 3) Серёжа не разбивал. 4) Вазу разбил Коля.
- Коля: 5) Я не разбивал. 6) Вазу разбил Серёжа.
Бабушка знала, что один из её внуков, назовём его правдивым, оба раза сказал правду; второй, назовём его шутником, оба раза сказал неправду; третий, назовём его хитрецом, один раз сказал правду, а другой раз — неправду. Назовите имена правдивого, шутника и хитреца. Кто из внуков разбил вазу?

Исходя из того, что знает о внуках бабушка, следует искать в таблице строку, содержащую в каком-либо порядке три комбинации значений: 00 (слова шутника), 11 (слова правдивого внука), 01 или 10 (слова хитреца). Такая строка отмечена галочкой. Согласно этой строке, вазу разбил Серёжа, он же оказался хитрецом. Шутником оказался Вася. Имя правдивого внука — Коля.
Задача 2. В соревнованиях по гимнастике участвуют Алла, Валя, Сима и Даша. Болельщики высказали предположения о возможных победителях:
- 1) Сима будет первой, Валя — второй;
- 2) Сима будет второй, Даша — третьей;
- 3) Алла будет второй, Даша — четвёртой.
По окончании соревнований оказалось, что в каждом из предположений только одно из высказываний истинно, другое ложно. Какое место на соревнованиях заняла каждая из девушек, если все они оказались на разных местах? Решение. Рассмотрим простые высказывания:
Так как в каждом из трёх предположений одно из высказываний истинно, а другое ложно, то можно заключить следующее:
Логическое произведение истинных высказываний будет истинным:
На основании распределительного закона преобразуем левую часть этого выражения:
Высказывание C1 • С2 означает, что Сима заняла и первое, и второе места. Согласно условию задачи, это высказывание ложно. Ложным является и высказывание В2 • С2. Учитывая закон операций с константой 0, запишем:
Дальнейшее преобразование левой части этого равенства и исключение заведомо ложных высказываний дают:
Из последнего равенства следует, что С1 = 1, Д3 = 1, А2 = 1. Это означает, что Сима заняла первое место, Алла — второе, Даша — третье. Следовательно, Валя заняла четвёртое место.
Логические элементы
Алгебра логики — раздел математики, играющий важную роль в конструировании автоматических устройств, разработке аппаратных и программных средств информационных и коммуникационных технологий.
Вы уже знаете, что любая информация может быть представлена в дискретной форме — в виде фиксированного набора отдельных значений. Устройства, которые обрабатывают такие значения (сигналы), называются дискретными. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом.
На рис. 1.5 приведены условные обозначения (схемы) логических элементов, реализующих логическое умножение, логическое сложение и инверсию.

Логический элемент И (конъюнктор) реализует операцию логического умножения (рис. 1.5, а). Единица на выходе этого элемента появится только тогда, когда на всех входах будут единицы.
Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения (рис. 1.5, б). Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица.
Логический элемент НЕ (инвертор) реализует операцию отрицания (рис. 1.5, в). Если на входе элемента 0, то на выходе 1 и наоборот.
Компьютерные устройства, производящие операции над двоичными числами, и ячейки, хранящие данные, представляют собой электронные схемы, состоящие из отдельных логических элементов. Более подробно эти вопросы будут раскрыты в курсе информатики 10-11 классов.
Пример 3. Проанализируем электронную схему, т. е. выясним, какой сигнал должен быть на выходе F при каждом возможном наборе сигналов A и B на входах.

Решение. Все возможные комбинации сигналов А и Б на входах внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную 4 схему.

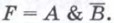
Таблицу истинности можно построить и по логическому выражению, соответствующему электронной схеме. Последний логический элемент в рассматриваемой схеме — конъюнктор. В него поступают сигналы от входа А и от инвертора. В свою очередь, в инвертор поступает сигнал от входа В. Таким образом,
Элементы алгебры логики. Самое главное
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.

Таблицы истинности для основных логических операций:

При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций:
На вводном уроке, посвящённом основам математической логики, мы познакомились с базовыми понятиями этого раздела математики, и сейчас тема получает закономерное продолжение. Помимо нового теоретического, а точнее даже не теоретического – а общеобразовательного материала нас ожидают практические задания, и поэтому если вы зашли на данную страницу с поисковика и/или плохо ориентируетесь в материале, то, пожалуйста, пройдите по вышеуказанной ссылке и начните с предыдущей статьи. Кроме того, для практики нам потребуется 5 таблиц истинности логических операций, которые я настоятельно рекомендую переписать от руки.
НЕ запомнить, НЕ распечатать, а именно ещё раз осмыслить и собственноручно переписать на бумагу – чтобы они были перед глазами:
– таблица НЕ;
– таблица И;
– таблица ИЛИ;
– импликационная таблица;
– таблица эквиваленции.
На самом деле с понятием логической формулы вы уже знакомы. Приведу стандартное, но довольно-таки остроумное определение: формулами алгебры высказываний называются:
1) любые элементарные (простые) высказывания ;
2) если и – формулы, то формулами также являются выражения вида
.
Никаких других формул нет.
Логическую формулу можно рассматривать, как логическую функцию. Запишем в функциональном виде ту же конъюнкцию:
Элементарные высказывания и в этом случае играют роль аргументов (независимых переменных), которые в классической логике могут принимать 2 значения: истина или ложь. Далее для удобства я буду иногда называть простые высказывания переменными.
– в первую очередь выполняется отрицание ;
– во вторую очередь – конъюнкция ;
– затем – дизъюнкция ;
– потом импликация ;
– и, наконец, низший приоритет имеет эквиваленция .
Наверное, все понимают, но на всякий пожарный: и – это две разные формулы! (как в формальном, так и в содержательном плане)
(три горизонтальные чёрточки – это значок тождества)
Составить таблицу истинности для формулы и убедиться в справедливости знакомого вам тождества .
Ещё раз повторим порядок решения задачи:
1) Так как в формулу входят две переменные, то всего будет 4 возможных набора нулей и единиц. Записываем их в оговорённом выше порядке.
И, наконец, сверяемся с таблицей истинности эквиваленции .
Основные равносильности алгебры высказываний
С двумя из них мы только что познакомились, но ими дело, понятно, не огранивается. Тождеств довольно много и я перечислю самые важные и самые известные из них:
Коммутативность конъюнкции и коммутативность дизъюнкции
Коммутативность – это перестановочность:
Ассоциативность логического умножения и сложения
Дистрибутивные свойства
Закон идемпотентности
Что делать, латынь.
И тут же несколько похожих тождеств:
…мда, что-то я даже подзавис… так и доктором философии завтра можно проснуться =)
Закон двойного отрицания
Законы поглощения
В правом тождестве скобки можно опустить.
Законы де Моргана
Предположим, что строгий Преподаватель (имя которого вам тоже известно:)) ставит экзамен, если – Студент ответил на 1-й вопрос и – Студент ответил на 2-й вопрос. Тогда высказывание , гласящее о том, что Студент не сдал экзамен, будет равносильно утверждению – Студент не ответил на 1-й вопрос или на 2-й вопрос.
Как уже отмечалось выше, равносильности подлежат доказательству, которое стандартно осуществляется с помощью таблиц истинности. В действительности мы уже доказали равносильности, выражающие импликацию и эквиваленцию, и сейчас настало время закрепить технику решения данной задачи.
Теперь убедимся, например, в справедливости закона де Моргана .
Доказать следующие равносильности:
Краткое решение в конце урока. Не ленимся! Постарайтесь не просто составить таблицы истинности, но ещё и чётко сформулировать выводы. Как я недавно отмечал, пренебрежение простыми вещами может обойтись очень и очень дорого!
Продолжаем знакомиться с законами логики!
Да, совершенно верно – мы с ними уже вовсю работаем:
Формула, которая принимает значение Истина при любом наборе значений входящих в неё переменных, называется тождественно истинной формулой или законом логики.
В силу обоснованного ранее перехода от равносильности к тождественно истинной формуле , все перечисленные выше тождества представляют собой законы логики.
Формула, которая принимает значение Ложь при любом наборе значений входящих в неё переменных, называется тождественно ложной формулой или противоречием.
Фирменный пример противоречия от древних греков:
– никакое высказывание не может быть истинным и ложным одновременно.
Однако и любое противоречие – это тоже закон логики, в частности:
Нельзя объять столь обширную тему в одной-единственной статье, и поэтому я ограничусь ещё лишь несколькими законами:
Закон исключённого третьего
Самостоятельно составьте табличку истинности и убедитесь в том, что это тождественно истинная формула.
Закон контрапозиции
Также из данного закона следует, что если справедливой является прямая теорема , то обязательно истинным будет и утверждение , которое иногда называют противоположной теоремой.
Если истинна обратная теорема , то в силу закона контрапозиции , справедлива и теорема, противоположная обратной:
Закон силлогизма
Ну и здесь опять хочется отметить формализм математической логики: если наш строгий Преподаватель думает, что некий Студент – есть дуб, то с формальной точки зрения данный Студент, безусловно, растение =) …хотя, если задуматься, то может быть и с неформальной тоже =)
Давайте на этой веселой ноте проведём доказательство. В данную формулу входят уже элементарных высказывания , а значит, всего будет: различных комбинаций нулей и единиц (см. три левых столбца таблицы). Заодно, кстати, записал вам общую формулу; с точки зрения комбинаторики, здесь размещения с повторениями.
Составим таблицу истинности для формулы . В соответствии с приоритетом логических операций, придерживаемся следующего алгоритма:
1) выполняем импликации и . Вообще говоря, можно сразу выполнить и 3-ю импликацию, но с ней удобнее (и допустимо!) разобраться чуть позже;
2) к столбцам применяем правило И;
3) вот теперь выполняем ;
4) и на завершающем шаге применяем импликацию к столбцам и .
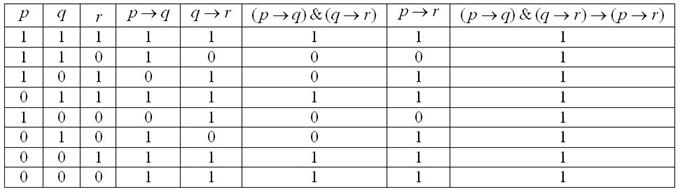
Не стесняйтесь контролировать процесс указательным и средним пальцем :))
Из последнего столбца, думаю, всё понятно без комментариев:
, что и требовалось доказать.
Выяснить, будет ли являться законом логики следующая формула:
Краткое решение в конце урока. Да, и чуть не забыл – давайте условимся перечислять исходные наборы нулей и единиц в точно таком же порядке, что и при доказательстве закона силлогизма. Строки конечно, можно и переставить, но это сильно затруднит сверку с моим решением.
Преобразование логических формул
Кроме того, есть ещё одна важная вещь: тождества справедливы не только для элементарных высказываний, но и для произвольных формул. Так, например:
, где – любые (сколь угодно сложные) формулы.
Преобразуем, например, сложную импликацию (1-е тождество):
Ну, а с коммутативностью вообще всё просто – даже обозначать ничего не нужно… что-то запал мне в душу закон силлогизма:))
Таким образом, закон можно переписать и в более затейливом виде:
В качестве тренировки упростим формулу .
Как правило, на первом шаге (шагах) избавляются от эквиваленции и импликации (если они есть) и сводят формулу к трём основным логическим операциям. Что тут скажешь…. Логично.
(1) Используем тождество . А нашем случае .
(2) К внешним скобкам применяем закон де Моргана , где .
(3) К внутренним скобкам применяем закон двойного отрицания . Внешние скобки можно убрать, т.к. за её пределами находятся равные по силе операции.
(4) В силу коммутативности дизъюнкции меняем местами и . Оставшиеся скобки тоже убираем по озвученной выше причине.
(5) В силу коммутативности дизъюнкции меняем местами и , а также и .
(6) Используем закон идемпотентности и закон исключенного третьего
(7) Дважды используем тождество
Вот оно как…, оказалось, что наша формула – тожественно истинна:
Желающие могут составить таблицу истинности и убедиться в справедливости данного факта.
Пара задач для закрепления материала:
Выразить эквиваленцию через отрицание, конъюнкцию, дизъюнкцию и раскрыть скобки
Аккуратно проводим преобразования в соответствии с равносильностями. После этого будет не лишним вернуться к параграфу об эквиваленции и найти там фразу, которая соответствует полученному результату ;-)
Упростить логическую формулу
Решения с подробными комментариями совсем близко.
Решения и ответы:
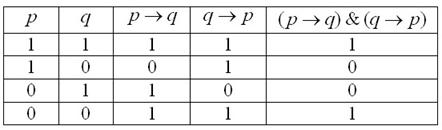
Задание 1 Решение: составим таблицу истинности для формулы :
(подробные инструкции по заполнению таблицы находятся после условия задачи)
Полученный результат совпадает с эквиваленцией высказываний и , таким образом:
Задание 2 Решение: доказательства проведём с помощью таблиц истинности:
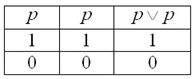
а) Дважды записываем все варианты истины и лжи высказывания и применяем к столбцам операцию ИЛИ:
Результат совпадает с . Тождество доказано
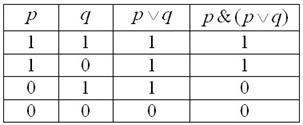
б) составим таблицу истинности для левой части тождества
. Сначала к столбцам и применяем операцию ИЛИ, затем к столбцам и – операцию И:
В результате истинность формулы совпала с истинностью высказывания , таким образом, тождество доказано.
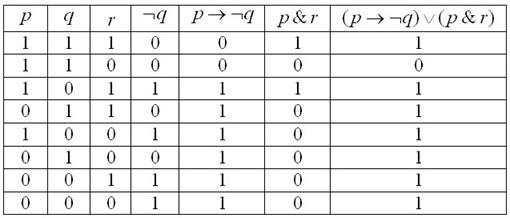
Задание 3 Решение: составим таблицу истинности:
Вывод: данная формула не является тождественно истинной (законом логики)
Задание 4 Решение:
(1) Используем тождество .
(2) Дважды применяем тождество .
(3) Используем дистрибутивный закон , в данном случае:
(квадратные скобки можно было не ставить – они не меняют порядок действий, но помогают лучше видеть ситуацию).
(4) В квадратных скобках используем коммутативность конъюнкции.
(5) Дважды используем тот же самый дистрибутивный закон.
(6) Во второй слева скобке используем коммутативность конъюнкции.
(7) Согласно закону противоречия: .
(8) К формуле дважды применяем тожество .
(9) А это уже для красоты :)) Скобки, кстати, можно было убрать намного раньше (я их не опускал с целью улучшить восприятие преобразований).
Задание 5 Решение:
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Читайте также:

