Как сделать кинематический анализ зубчатого механизма
Обновлено: 02.07.2024
энергии не претерпевает разделения по нескольким потокам. Однако в некоторых случаях условия технического задания не позволяют использовать подобные механизмы. В этом случае применяются многопоточные механизмы(рис. 7.3, а).
Многопоточный зубчатый механизм – это сложный зубчатый меха-
низм, структура которого содержит кинематические цепи, образующие не-
сколько замкнутых контуров, и входной поток механической энергии в про-
цессе передачи и преобразования делится по нескольким потокам, а затем
суммируется в один поток на выходном звене.
Разделение входного потока механической энергии по нескольким по-
токам позволяет распределить действие силовых факторов по большему чис-
лу кинематических пар, что приводит к снижению значений реакций связей и
позволяет уменьшить габаритные размеры и массу механизмов.
Структурный анализ. Схема сложного многопоточного зубчатого ме-
ханизма (рис. 7.3, а) образована последовательным и параллельным соедине-
нием простых зубчатых механизмов, относящихся к плоским механизмам,
следовательно, рассматриваемый механизм также является плоским, под-
вижность которого определяется по формуле Чебышева.
Из анализа схемы механизма (рис. 7.3, а) вытекает: структура многопо-
точного зубчатого механизма состоит из стойки 0, представленной тремя
шарнирно неподвижными опорами, двух блоков зубчатых колес 1 и 2 и под-
вижного звена 4. Колеса 2 и 3 входят в состав блока зубчатых колес, рас-
сматриваются как одно звено. Схема механизма содержит избыточную связь,
представленную вторым блоком колес 2 и 3. Избыточная связь введена в
структуру механизма с целью уменьшения значений силовых факторов, дей-
ствующих в зацеплениях зубьев колес 1 и 2, 3 и 4. Следовательно, при опре-
делении подвижности необходимо исключить из схемы механизма дефекты
структуры, т. е. второй блок колес 2 и 3. В этом случае n = 3 .
Стойка 0 с подвижными звеньями 1, 2, 4 создает три одноподвижные
кинематические пары: 0 – 1, 2 – 0, 4 – 0, а зубчатые колеса 1, 2, 4 между со-
бой образуют две высшие кинематические пары: 1 – 2, 3 – 4 с подвижностью,
равной двум. Дополнительные ряды колес 1−2 и 3−4 (рис. 7.3, а) являются
избыточной связью, поэтому подвижность данных кинематических пар не
учитываем, тогда p1 = 3, а 2 p = 2.
Подставив полученные результаты в формулу Чебышева, получим
W = 3⋅3 − 2 ⋅3 − 2 =1.
Результат означает, что для однозначного определения взаимного рас-
положения звеньев сложного многопоточного зубчатого механизма
(рис. 7.3, а) достаточно одной обобщенной координаты.
Кинематический анализ. Прямое передаточное отношение сложного
многопоточного зубчатого механизма от шестерни 1 к выходному колесу 4

(рис. 7.3, а) выражается в виде
вращаются в разных направлениях. Анализ выражения показывает, что пере-
данное отношение сложного многорядного зубчатого механизма зависит от
параметров колес, его образующих.

Сложные многопоточные зубчатые механизмы являются реверсивными и могут работать в режиме редуктора и в режиме мультипликатора, следовательно, для механизмов данного вида характерно наличие как прямого, так и обратного передаточного отношения:

Взаимосвязь линейных и угловых скоростей подвижных звеньев слож-
ного многорядного многопоточного зубчатого механизма (рис. 7.3, а) на-
глядно характеризуется при помощи планов линейных и угловых скоростей
(рис. 7.3, б, в).

Для определения значений угловых скоростей ведомых звеньев составим пропорцию:
где 01 , 02 , 03 − отрезки с плана угловых скоростей.
Угловые скорости звеньев 2, 3 и 4, с−1:

С целью проверки правильности построения планов выразим переда-
точное отношение однорядного планетарного механизма через элементы

плана угловых скоростей:
ков 01 и 04 на плане угловых скоростей (рис. 7.3, в).
57. Эпициклические зубчатые механизмы. Типовые планетарные механизмы. Звенья планетарных механизмов. Особенности структуры. Пример выполнения структурного механизма.
Однорядные, многорядные и многопоточные зубчатые механизмы являются представителями сложных зубчатых механизмов с неподвижными
осями вращения зубчатых колес. С помощью механизмов перечисленных
видов не всегда удается обеспечить выполнение заданных условий. В этом
случае применяются сложные зубчатые механизмы с подвижными геометрическими осями вращения колес. Подобные механизмы называются эпициклическими.
Эпициклический зубчатый механизм – это сложный зубчатый механизм, имеющий в своей структуре хотя бы одно звено с подвижной геометрической осью вращения.
К эпициклическим зубчатым механизмам относятся: планетарные
(рис. 7.4) и дифференциальные механизмы (рис. 7.9, а).
Планетарный зубчатый механизм – это эпициклический зубчатый механизм с подвижностью, равной единице.
К типовым планетарным механизмам относятся:
однорядный планетарный зубчатый механизм с одним внешним и од-
ним внутренним зацеплением (рис. 7.4, а);
двухрядный планетарный зубчатый механизм с одним внешним и од-
ним внутренним зацеплением (рис. 7.4, б);
двухрядный планетарный зубчатый механизм с двумя внешними зацеплениями (рис. 7.4, в);
двухрядный планетарный зубчатый механизм с двумя внутренними зацеплением (рис. 7.4, г).

Независимо от схемы (рис. 7.4), структура планетарных зубчатых механизмов содержит следующие звенья: солнечное колесо, корона, один или
нескольких сателлитов и водило.
Солнечное колесо – это зубчатое колесо с внешними зубьями, расположенное в центре планетарного механизма.
Корона – это зубчатое колесо планетарного механизма с внутренними
Сателлит – это зубчатое колесо планетарного механизма, геометрическая ось вращения которого является подвижной.
Водило – это подвижное звено планетарного механизма, на котором установлены сателлиты.
Солнечное колесо в схемах планетарных механизмов (рис. 7.4, а−в) представлено подвижным звеном 1, а в схеме (рис. 7.4, г) солнечное колесо отсутствует. При этом схема планетарного механизма (рис. 7.4, в) помимо подвижного солнечного колеса 1 содержит и неподвижное солнечное колесо 4. Короной в
схемах планетарных механизмов (рис. 7.4, а, б, г) является неподвижное
колесо 4, а в схеме (рис. 7.4, в) корона отсутствует. При этом схема планетарного механизма (рис. 7.4, г) помимо неподвижной короны 4 содержит и подвижную корону 1. Сателлитом в планетарных механизмах является подвижное колесо 2. В схеме (рис. 7.4, а) сателлит представлен одним колесом, а в схемах (рис. 7.4, б−г) сателлит – это блок зубчатых колес 2 и 3. Водило во всех схемах планетарных механизмов представлено в виде рычажной системы H и предназначено для установки сателлитов и обеспечения вращательного движения этих звеньев как вокруг собственной оси вращения, так и вокруг оси вращения водила Н. В зависимости от схемы планетарного механизма возможная реализация сочетаний значений КПД и величин передаточных чисел представлена

Структурный анализ. Все схемы планетарных механизмов (рис. 7.4) образованы последовательным соединением простых зубчатых механизмов, которые являются плоскими механизмами. Следовательно, для определения
подвижности данного механизма можно воспользоваться формулой Чебышева. Из анализа схем планетарных механизмов (рис. 7.4) вытекает: все планетарные механизмы состоят из стойки 0, трех подвижных звеньев 1, 2 и Н. Корона 4 является неподвижным звеном, следовательно, является элементом стойки 0. В этом случае n = 3 .
Все схемы планетарных механизмов (рис. 7.4) содержат по три одноподвижные кинематические пары: 0 – 1, 2 – H, H – 0 и по две высшие кинематические пары: 1 – 2, 2 – 0 с подвижностью, равной двум, тогда p1 = 3, а p2 = 2.
Подставив значения коэффициентов в формулу Чебышева, получим
W = 3⋅3 − 2 ⋅3 − 2 =1.
Результат означает, что для однозначного определения взаимного рас-
положения звеньев любой схемы типового планетарного механизма (рис. 7.4)
достаточно одной обобщенной координаты.
Формула Виллиса
Формула Виллиса выводится на основании основной теоремы зацепления и устанавливает соотношение между угловыми скоростями зубчатых колес в планетарном механизме. Рассмотрим простейший планетарный механизм с одним внешним зацеплением (см. рис. 15.3). Число подвижностей в этом механизме равно то есть для получения определенности движения звеньев механизма необходимо сообщить независимые движения двум его звеньям. Рассмотрим движение звеньев механизма относительно стойки и относительно водила. Угловые скорости звеньев в каждом из рассматриваемых движений приведены в таблице 15.2.
В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила. Если в движении относительно стойки ось зубчатого колеса 2 подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления.



Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.

Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор.

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.).
Краткое содержание: Сложные зубчатые механизмы. Многоступенчатые и планетарные механизмы. Кинематика рядного и ступенчатого зубчатого механизма. Формула Виллиса для дифференциальных механизмов. Кинематическое исследование типовых планетарных механизмов графическим и аналитическим методами. Постановка задачи синтеза планетарных механизмов. Условия подбора чисел зубьев. Условия соосности, соседства и сборки. Примеры решения задач по подбору чисел зубьев.
При проектировании зубчатых механизмов многих машин и приборов возникает необходимость обеспечить передачу вращения с большим передаточным отношением или при значительных межосевых расстояниях. В таких случаях применяют многозвенные зубчатые механизмы – либо редукторы, снижающие скорость вращения выходного вала по сравнению со скоростью входного звена, либо мультипликаторы, повышающие ее.
Многозвенные зубчатые механизмы подразделяются на два вида: 1) механизмы с неподвижными осями всех колес (рядовые и ступенчатые зубчатые механизмы); 2) механизмы, в которых оси отдельных колес перемещаются относительно стойки (планетарные и дифференциальные механизмы).
Механизмы с неподвижными осямизубчатых колес имеют число степеней свобод, равное единице, благодаря чему передаточное отношение постоянно.
Общее передаточное отношение многозвенного зубчатого механизма равно произведению передаточных отношений отдельных ступеней:
Рядовые зубчатые механизмы представляют собой последовательное соединение нескольких пар зубчатых колес (рис. 14).
Общее передаточное отношение рядового зубчатого механизма постоянно и равно обратному отношению чисел зубьев или радиусов крайних колес:
Знак передаточного отношения определяется множителем , где - число передач внешнего зацепления. Но передаточное отношение в таких передачах невелико, так как оно ограничено допустимой величиной и , а числа зубьев промежуточных колес не влияют на величину общего передаточного отношения механизма, поэтому их называют паразитными колесами.

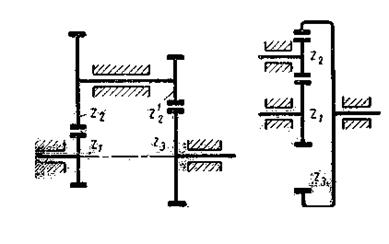
Ступенчатые зубчатые механизмы (рис. 15) представляют собой последовательное соединение блочных (спаренные колеса 1 и 2; 2 ” и 3) или одиночных зубчатых колес. В общем случае при j колесах и t внешних зацеплениях полное передаточное отношение ступенчатой передачи
т.е. равно отношению произведения чисел зубьев ведомых колес к произведению ведущих колес.
Зубчатые механизмы с подвижными осямиимеют колеса с движущимися геометрическими осями, которые называются саттелитами. На рис. 16 показана схема планетарного механизма: подвижное звено – h, в котором помещены оси саттелитов, называется водилом; вращающееся неподвижной оси колесо – 1, по которому обкатываются саттелиты, называется центральным; неподвижное центральное колесо – 3 называется опорным. Как правило, планетарные механизмы изготовляются соосными, это означает, что оси колес 1, 3 и водила h находятся на одной прямой.
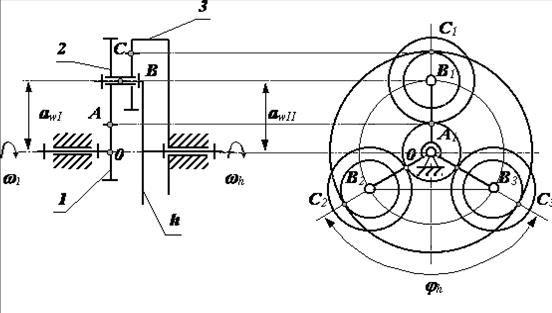
Обычно у реального механизма имеется несколько симметрично расположенных саттелитов. Их вводят для того, чтобы снизить усилия в зацеплении, разгрузить подшипники центральных колес, улучшить уравновешивание водила. Но при кинематических расчетах учитывается только один саттелит, так как остальные являются пассивными в кинематическом отношении.
Аналитический метод исследования планетарных механизмов основан на способе обращения движения. Всем звеньям механизма сообщается угловая скорость, равная по величине и противоположная по направлению угловой скорости водила . Тогда водило становится неподвижным, и механизм из планетарного обращается в зубчатый механизм, состоящий из нескольких последовательно соединенных пар зубчатых колес (1,2 и 2`3). Передаточные отношения планетарного механизма и обращенного механизма связаны условием:
Эта формула справедлива для любой схемы планетарного редуктора при наличии неподвижного центрального колеса. Значит, передаточное отношение от любого саттелита k к водилу при неподвижном опорном колесе j равно единице минус передаточное отношение от этого же колеса к опорному в обращенном механизме:
Если в планетарном механизме (рис. 16) освободить от закрепления опорное колесо 3 и сообщить ему вращательное движение, то механизм превратится в дифференциал со степенью свободы W = 2 (рис. 17).
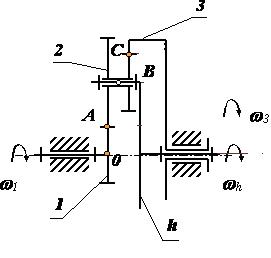
Для кинематического исследования дифференциальных механизмов используются формула Виллиса, полученная так же на основе метода обращения движения:
Где - передаточное отношение в обращенном движении ( ).
Графическое определение передаточного отношения многозвенных механизмов зубчатых можно осуществить методом планов скоростей (треугольников скоростей). Треугольники скоростей можно построить, если известны линейные скорости не менее двух точек звена (по величине и направлению). Используя этот метод и построив треугольники скоростей (рис.18), можно получить наглядное представление о характере изменения скоростей от одного вала к другому, и можно определить графически угловую скорость любого звена (колеса).
Исходные данные: m – модуль зацепления, zi- числа зубьев колес, .
Определить передаточное отношение механизма .
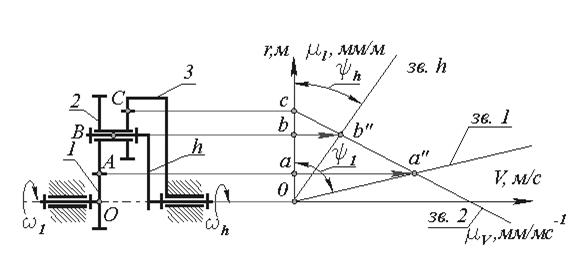
Решение. Построим кинематическую схему механизма в масштабе , определив радиусы делительных окружностей зубчатых колес
Найдем линейную скорость т. А в зацеплении звеньев 1 и 2
В системе координат r0V построим треугольники распределения линейных скоростей звеньев. Для этого из точки а с ординатой r1 в выбранном произвольном масштабе отложим отрезок aa”. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на оси r1. Эта прямая образует с осью r1 угол . Так как в точке C скорости звеньев 2 и 3 равны между собой и равны нулю, то, соединяя точку C прямой с точкой a”, получим линию распределения скоростей для звена 2. Так как точка B принадлежит звеньям 2 и h, то ее скорость определяется по лучу сa” для радиуса равного rB = (r1+r2), что в масштабе соответствует отрезку bb”. Соединяя точку b” с началом координат прямой, найдем линию распределения скоростей для водила. Эта линия образует с осью r угол . Передаточное отношение планетарного механизма, определенное по данным графическим построениям, можно записать так
Постановка задачи синтеза планетарных механизмов.
При проектировании планетарных механизмов необходимо, кроме требований технического задания (заданного передаточного отношения), выполнять ряд условий связанных с особенностями планетарных и многопоточных механизмов. Задача проектирования и в этом случае может быть разделена на структурный и метрический синтез механизма. При структурном синтезе определяется структурная схема механизма, при метрическом - определяются числа зубьев колес, так как радиусы зубчатых прямо пропорциональны числам зубьев
ri = m × zi / 2.
Для типовых механизмов первая задача сводится к выбору схемы из набора типовых схем. При этом руководствуются рекомендуемым для схемы диапазоном передаточных отношений и примерными оценками ее КПД. После выбора схемы механизма необходимо определить сочетание чисел зубьев его колес, которые обеспечат выполнение условий технического задания - для редуктора это передаточное отношение и величина момента сопротивления на выходном валу. Передаточное отношение задает условия выбора относительных размеров зубчатых колес - чисел зубьев колес, крутящий момент задает условия выбора абсолютных размеров - модулей зубчатых зацеплений. Так как для определения модуля необходимо выбрать материал зубчатой пары и вид его термообработки, то на первых этапах проектирования принимают модуль зубчатых колес равным единице, то есть решают задачу кинематического синтеза механизма в относительных величинах.
При кинематическом синтезе (подборе чисел зубьев колес) задача формулируется так: для выбранной схемы планетарного механизма при числе сателлитов и заданном передаточном отношении необходимо подобрать числа зубьев колес, которые обеспечат выполнение ряда условий.

Угловая скорость входного звена зубчатого механизма d = 104 рад/с.
Общее передаточное уравнение редуктора равно:

где - передаточное отношение зубчатой передачи.




С другой стороны передаточное отношение равно:

Следовательно угловая скорость выходного звена будет равна:



Построение плана положений механизма
На листе формата А1 изображаем в масштабе план положений механизма. План строим в такой последовательности. Выбираем масштаб построения:


Выбираем произвольную точку О и из нее описываем окружность радиуса ОА. Начальное положение точки А (АО) выбираем согласно заданию в крайнем левом положении ползуна D. В этом положении точка В коромысла BC находится в наименьшем удалении от центра вращения кривошипа - точки О. От точки АО в направлении вращения кривошипа ОА разбиваем окружность на 12 равных частей, через каждые 30 градусов, проставляя при этом последовательно точки А1, А2 и т. д. Соединив полученные точки с центром окружности О, получим 12 положений кривошипа ОА. Точка В принадлежит коромыслу ВС и движется вращательно по окружности с центром в точке С, поэтому для построения плана положений звена АВ из каждой точки А откладываем длину шатуна АВ, в принятом масштабе, до пересечения с траекторией движения точки В, получая точки В1, В2 и т. д. Далее, таким же образом откладываем из каждой полученной точки длину шатуна BD до пересечения с линией движения ползуна, получая точки D1, D2 и т. д.
Целью кинематического анализа является определение угловых скоростей звеньев и передаточных отношений.
Передаточное отношение между звеньями a и b определяется как отношение их угловых скоростей (или частот вращения):

. (3.1)
Угловые скорости и частоты вращения связаны соотношениями
; .
Очевидно, что перестановка индексов у величины приводит к получению обратной величины, т.е..
любое из двух возможных направлений вращения принимают за положительное (обычно положительным считают направление вращения входного вала механизма), тогда угловая скорость каждого звена кинематической цепи приобретает вполне определенный знак;
при одинаковом направлении угловых скоростей, входящих в (3.1), они имеют одинаковые знаки и, следовательно, определяют положительное передаточное отношение.



, (3.2)
а для пары внешнего зацепления (рис. 3.2) -

. (3.3)
3.1. Кинематика рядовых механизмов
Зубчатый механизм, у которого все звенья вращаются вокруг неподвижных осей, называют рядовым. Такой механизм может быть одноступенчатым (рис. 3.1 и 3.2) и многоступенчатым (рис. 3.3 и 3.4).
В многоступенчатом рядовом механизме число ступеней совпадает с числом зацеплений, его общее передаточное отношение определяют как произведение передаточных отношений всех последовательно соединенных ступеней.



Так, для трехступенчатого механизма по рис. 3.3 общее передаточное отношение определится по формуле

.
На рис. 3.4 также представлен трехступенчатый механизм, у которого колеса образуют соосную кинематическую цепь, причем колесоучаствует одновременно в двух зацеплениях – в одном как ведомое, в другом как ведущее (такие колеса называютсвязанными); для этого механизма

.
Отметим, что при (выходной валB вращается медленнее входного вала A) механизм называют редуктором, а при –мультипликатором.
3.2. Кинематика планетарных и дифференциальных механизмов
Планетарные и дифференциальные механизмы включают в себя колеса, оси которых являются подвижными. Рычаг, на котором расположены эти оси, называют водилом, а колеса с подвижными осями – сателлитами. Неподвижная ось вращения водила является центральной осью механизма. Колеса, которые вращаются или могут вращаться относительно центральной оси и при этом зацепляются с сателлитами, называют центральными или солнечными.
В планетарную ступень входят: водило; сателлиты, размещенные на этом водиле; колеса, которые зацепляются с этими сателлитами.


Колесо и водилоH вращаются относительно центральной оси механизма.

Сателлит совершает сложное движение, состоящее из двух вращательных: вокруг своей геометрической оси и одновременно, вместе с водилом, вокруг центральной оси механизма.
У этого механизма две степени свободы

,
поэтому его называют дифференциальным механизмом, или дифференциалом. Кинематику такого механизма можно описать формулой

; (3.4)
здесь – абсолютные угловые скорости соответствующих звеньев (величины алгебраические – положительные или отрицательные),– передаточное отношениеобращенного механизма (т.е. такого воображаемого рядового механизма, который получают из заданного планетарного мысленной остановкой водила).
Из (3.4) видно, что для кинематической определимости этого механизма из трех угловых скоростей две должны быть заданы, т.е. механизм действительно является дифференциалом.
Общий вид формулы (3.4), пригодный для описания кинематики практически любого планетарного механизма, имеет вид

; (3.5)

ее называют формулой Р. Виллиса. Здесь a и b – любые два колеса одной и той же планетарной ступени, – передаточное отношение отa к b в обращенном (рядовом) механизме, это отношение всегда выражается через числа зубьев колес.
Величины угловых скоростей имогут быть любыми; в частности, при(т.е. колесо b неподвижно) отношение , и тогда формула Р. Виллиса приобретает вид

. (3. 6)
Формула (3.5) более универсальна и пригодна для любого планетарного механизма, тогда как (3.6) можно применять только для таких планетарных ступеней, у которых имеются неподвижные колеса (рис. 3.6 – 3.8).



Рис. 3.6
Рис. 3.7
Рис. 3.8
На рис. 3.6 показана схема редуктора Джемса с двухвенцовым сателлитом. Для него

, (3. 7)
передаточное отношение обращенной ступени

; (3. 8)
сопоставляя (3.7) и (3.8), найдем передаточное отношение редуктора

. (3. 9)
Таким же способом найдем передаточное отношение редуктора Джемса с одновенцовым сателлитом (рис. 3.7):

, (3.10)

; (3.11)

. (3. 12)

Для редуктора Давида (рис. 3.8), также имеющего неподвижное колесо в составе ступени, входным звеном является водило H, что отличает эту схему от двух других при выводе формулы для :

; (3.13)

; (3. 14)

. (3. 15)
В этих примерах показано применение формулы Виллиса в виде (3.6), хотя было бы вполне корректным и допустимым использование ее в виде (3.5).
Все схемы по рис. 3.6 – 3.8 имеют в своем составе три центральных звена – два центральных колеса и водило; каждое из этих звеньев нагружено вращающим моментом либо от источника движения, либо от потребителя мощности (ведомого звена), либо моментом от стойки. Такие звенья называют основными и в соответствии с их видом и количеством (в данном случае – два колеса и водило) подобным схемам присвоено обозначение типа 2KH.


Найдем передаточное отношение этого механизма:

. (3.16)
Обращенный механизм для данной схемы представляет собой разветвляющуюся рядовую кинематическую цепь, каждой из двух ее ветвей соответствует свое передаточное отношение:
; . (3.17)
После очевидных подстановок получаем

. (3.18)
Читайте также:

