Как сделать из четырехугольника 3 четырехугольника
Обновлено: 05.07.2024
Определение 1. Четырехугольник − это замкнутая ломаная линия, состоящая из четырех звеньев.
Определение 2. Четырехугольник − геометрическая фигура (многоугольник), состоящая из четырех точек, никакие три из которых не лежат на одной прямой и последовательно соединенные четырьмя отрезками, называемыми сторонами четырехугольника.
Объединение четырехугольника и ограниченной им части плоскости также называют четырехугольником.
Любой четырехугольник разделяет плоскость на две части, одна из которых называется внутренней областью четырехугольника, а другая внешней областью четырехугольника.
Виды четырехугольников
Четырехугольники бывают следующих видов:
-
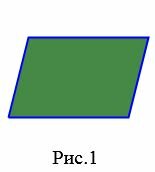
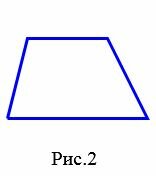
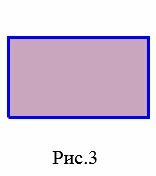
− четырехугольник, у которого противоположные стороны попарно вправны и параллельны (Рис.1). − четырехугольник, у которого две противоположные стороны параллельны (Рис.2). − четырехугольник, у которого все углы прямые (Рис.3).
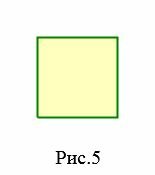
- Ромб − четырехугольник, у которого все стороны равны (Рис.4). − четырехугольник, у которого все стороны равны и все углы прямые (Рис.5).
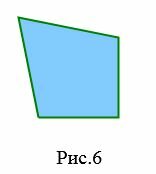
- Дельтоид − четырехугольник, у которого есть две пары равных смежных сторон (Рис.6, Рис.6.1).
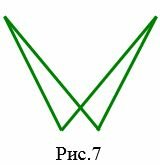
- Антипараллелограмм (или контрпараллелограмм)− четырехугольник, у которого противоположные стороны равны но не параллельны (с самопересечением) (Рис.7).
        |
Обозначение четырехугольника
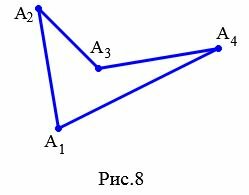
Обозначают четырехугольник буквами, стоящих при его вершинах. Называют четырехугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, четырехугольник на рисунке 8 называют \( \small A_1A_2A_3A_4 \) или \( \small A_4A_3A_2A_1 \) (Рис.8).
 |
Соседние вершины четырехугольника
Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.
На рисунке 8 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны четырехугольника
Стороны четырехугольника называются смежными, если они имеют общую вершину.
На рисунке 8 стороны \( \small A_2A_3 \) и \( \small A_3A_4 \) являются смежными, так как они имеют общую вершину \( \small A_3. \)
Простой четырехугольник. Самопересекающийся четырехугольник
Четырехугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
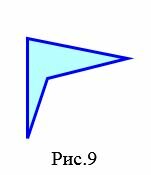  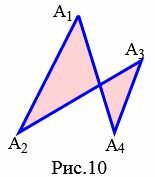 |
На рисунках 9 и 9.1 изображены простые четырехугольники так как стороны четырехугольников не имеют самопересечений. А на рисунке 10 четырехугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой четырехугольник называется самопересекающийся.
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
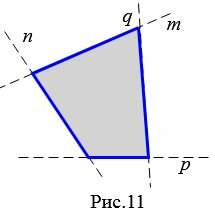 |
На рисунке 11 четырехугольник лежит по одну сторону от прямых \( \small m, \ n, \ p, \ q, \) проходящих через стороны четырехугольника. Поэтому такой четырехугольник выпуклый.
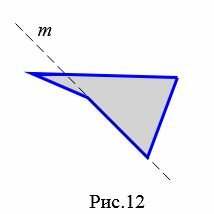 |
На рисунке 12 прямая \( \small m\) делит четырехугольник на две части, т.е. четырехугольник не лежит по одну сторону от прямой \( \small m\). Следовательно, этот четырехугольник не является выпуклым.
Правильный четырехугольник
Простой четырехугольник называется правильным, если все его стороны равны и все углы равны. Квадрат является правильным четырехугольником, так как все его стороны равны и все его углы равны 90°. Среди четырехугольников других правильных четырехугольников не существует.
На рисунке 5 изображен правильный четырехугольник (квадрат), так как у данного четырехугольника все стороны равны и все углы равны. Четырехугольник (ромб) на на рисунке 4 не является правильным, так как все стороны четырехугольника равны, но все его углы не равны друг другу. Прямоугольник также не является правильным четырехугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Периметр четырехугольника
Сумма всех сторон четырехугольника называется периметром четырехугольника. Для четырехугольника \( \small A_1A_2A_3A_4 \) периметр вычисляется из формулы:
Угол четырехугольника
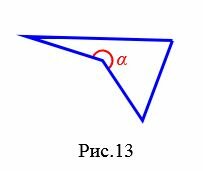
Углом (внутренним углом) четырехугольника при данной вершине называется угол между двумя сторонами четырехугольника, сходящимися к этой вершине. Если четырехугольник выпуклый, то все углы четырехугольника меньше 180°. Если же четырехугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small \alpha \) на рисунке 13).
 |
Внешний угол четырехугольника
Внешним углом четырехугольника при данной вершине называется угол смежный внутреннему углу четырехугольника при данной вершине.
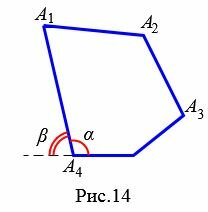 |
На рисунке 14 угол α является внутренним углом четырехугольника при вершине \( \small A_4, \) а углы β и γ являются внешними углами четырехугольника при этой же вершине. Очевидно, что при каждой вершине есть два внешних угла.
Диагональ четырехугольника
Диагоналями называют отрезки, соединяющие две несоседние вершины четырехугольника.
Очевидно, что у четырехугольника две диагонали.
Сумма углов четырехугольника
Для любого простого четырехугольника по крайней мере один диагональ делит его на два треугольника. Сумма углов треугольника равна 180°. Поэтому сумма углов простого четырехугольника равна 360°.
Сумма внешних углов четырехугольника
Пусть задан четырехугольник \( \small A_1A_2A_3A_4 .\) Внешний угол при вершине \( \small A_1\) равен \( \small 180°-\angle A_1.\) Аналогично, внешние углы при вершинах \( \small A_2, \ A_3, \ A_4 \) равны \( \small 180°-\angle A_2, \) \( \small 180°-\angle A_3, \) \( \small 180°-\angle A_4, \) соответственно. Тогда сумма внешних углов четырехугольника равна:
| \( \small 180°-\angle A_1 \) \( \small +180°-\angle A_2 \) \( \small +180°-\angle A_3 \) \( \small +180°-\angle A_4 \)\( \small =720°-(\angle A_1+\angle A_2+\angle A_3+\angle A_4 )\) \( \small =720°-360°=360°. \) |
Задача 1. Доказать, что длина любой стороны четырехугольника меньше суммы длин трех его сторон.
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.
Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .
Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .
Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .
Диагонали выпуклого четырехугольника пересекаются в одной точке.
Площадь произвольного выпуклого четырехугольника можно найти по формуле:
S = 1 2 d 1 d 2 ⋅ sin φ
где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).
Рассмотрим более подробно некоторые виды выпуклых четырехугольников.
Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.
Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180 ° .
- Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )
Площадь параллелограмма можно найти по трём формулам.
Как произведение стороны и высоты, проведенной к ней.
Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.
Как произведение двух смежных (соседних) сторон на синус угла между ними.
Как полупроизведение диагоналей на синус угла между ними.
Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
- Диагонали пересекаются под прямым углом.
- Диагонали являются биссектрисами углов, из которых выходят.
- Сохраняются все свойства параллелограмма.
Площадь ромба можно найти по трём формулам.
Как произведение стороны ромба на высоту ромба.
Как квадрат стороны ромба на синус угла между двумя сторонами.
Как полупроизведение диагоналей ромба.
Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Сохраняются все свойства параллелограмма.
Площадь прямоугольника можно найти по двум формулам:
Как произведение двух смежных (соседних) сторон прямоугольника.
Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.
Квадрат – прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Сохраняет свойства ромба.
- Сохраняет свойства прямоугольника.
Площадь квадрата можно вычислить по двум формулам:
Как квадрат стороны.
Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
Стороны, которые параллельны друг другу называются основаниями , другие две стороны называются боковыми сторонами .
B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .
Свойства трапеции:
сумма углов, прилежащих к боковой стороне, равна 180 ° .
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2
Площадь трапеции можно найти по двум формулам:
Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.
Как полупроизведение диагоналей на синус угла между ними.
Виды трапеций
Прямоугольная трапеция – трапеция, у которой два угла прямые.
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.

Четырехугольником ABCD называется фигура, которая состоит из четырех точек А, В, С, D по три, не лежащих на одной прямой, и четырех отрезков AB, BC, CD и AD, соединяющих эти точки.
На рисунках изображены четырехугольники.

Точки А, В, С и D называются вершинами четырехугольника, а отрезки AB, BC, CD и AD - сторонами. Вершины А и С, В и D называются противолежащими вершинами. Стороны AB и CD, BC и AD называются противолежащими сторонами.
Четырехугольники бывают выпуклые (на рисунке - левый) и невыпуклые (на рисунке - правый).
Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника (диагональ АС разделяет ABCD на два треугольника ABC и ACD; диагональ BD - на BCD и BAD). У невыпуклого четырехугольника только одна из диагоналей разделяет его на два треугольника (диагональ AC разделяет ABCD на два треугольника ABC и ACD; диагональ BD - не разделяет).

Рассмотрим основные виды четырехугольников, их свойства, формулы площади:
Параллелограмм
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
 | ABCD-параллелограмм: AB||DC, AD||BC |
Свойства:
Признаки параллелограмма:
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Площадь параллелограмма:

Трапеция
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Основаниями называются параллельные стороны, а две другие стороны - боковыми сторонами.

| Трапеция называется равнобедренной, если ее боковые стороны равны. |  |
| Трапеция, один из углов которой прямой, называется прямоугольной. |  |
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
ТЕОРЕМА.
Средняя линия трапеции параллельна основаниям и равна их полусумме.

Площадь трапеции:

Ромбом называется параллелограмм, у которого все стороны равны.
Свойства:
Площадь ромба:

Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы равны.
Свойства:
Признак прямоугольника:
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Площадь прямоугольника:

Квадрат
Квадратом называется прямоугольник, у которого все стороны равны.
Свойства:
Квадрат обладает всеми свойствами прямоугольника и ромба (прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом).
Площадь квадрата:

Автор: Аникина Марина
Комментарии к этой заметке:
Очень понравилась эта статья ) Все интересно и понятно) Очень помогло! Спасибо)
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Определение
Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.
- Противоположные стороны прямоугольника равны (АВ=CD, ВС=АD).
- Диагонали прямоугольника равны (АС=ВD).
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Периметр прямоугольника – это сумма длин всех сторон: Р=(а + b) × 2, где а и b соседние (смежные) стороны прямоугольника
- Площадь прямоугольника – это произведение длин соседних (смежных) сторон, формула для нахождения площади прямоугольника:
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
- Диагонали квадрата равны (BD=AC).
- Диагонали квадрата пересекаются под углом 90 градусов.
- Диагонали квадрата точкой пересечения делятся пополам (BO=OD, AO=OC).
- Периметр квадрата – это сумма длин всех сторон. Так как все стороны квадрата равны, то его можно найти по формуле Р=4×а, где а — длина стороны квадрата.
- Площадь квадрата – это произведение длин соседних сторон, формула для нахождения площади прямоугольника S=a 2 , где a — длина стороны квадрата.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
- Противолежащие стороны равны (АВ=CD, BC=AD).
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам (AO=OC, BO=OD).
- У параллелограмма противоположные углы равны (угол А равен углу С, угол В равен углу D).
- Сумма углов, прилежащих к одной стороне, равна 180 градусов.
- Периметр параллелограмма Р=(а + b) × 2, где а и b соседние (смежные) стороны параллелограмма.
- Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне, т.е. по формуле S=a×h
Ромб – это параллелограмм, у которого все стороны равны.

- Противоположные углы равны (угол А равен углу С, угол В равен углу D).
- Диагонали пересекаются под углом 90 градусов.
- Диагонали точной пересечения делятся пополам (AO=OC, BO=OD).
- Сумма углов, прилежащих к одной стороне, равна 180 градусов.
- Диагонали ромба являются биссектрисами его углов, т.е. делят углы пополам.
- Периметр ромба Р=4а, где а — длина стороны ромба.
- Площадь ромба S=ah, где а – сторона ромба, а h – высота, проведенная к этой стороне.
- Площадь ромба можно вычислить через известные длины его диагоналей, т.е. S= 1 2 . . d1d2.
Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
- Сумма углов, прилежащих к боковой стороне, равна 180 градусов
- Площадь трапеции равна произведению полусуммы оснований, на высоту. Она вычисляется по формуле S= a + b 2 . . h , где a и b – основания, а h – высота трапеции.
Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.
углы А и С равны по 90 градусов
Средняя линия трапеции

Определение Средняя линия трапеции – линия, проходящая через середины боковых сторон трапеции. Свойство средней линии: средняя линия параллельна основаниям и равна их полусумме. На рисунке средней линией является отрезок MN. Видим, что MN||BC, MN||AD. По определению MN= B C + A D 2
Задание 24OM21R Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке N, лежащей на стороне ВС. Докажите, что N – середина ВС.
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.

Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите боковую сторону АВ трапеции ABCD, если углы АВС и BCD равны соответственно 30 0 и 135 0 , а СD =17
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.

Рассмотрим треугольник CНD, где CD=17, угол Н=90 0 , следовательно, треугольник прямоугольный. Найдем величину угла DCН, 135 0 – 90 0 =45 0 (так как провели высоту CН). Отсюда следует, что угол D=45 0 , так как треугольник прямоугольный. Значит, треугольник является равнобедренным (углы D и DCН равны по 45 градусов).
Найдем катеты CН и DН по теореме Пифагора, как катет равнобедренного треугольника по формуле с=а √ 2 , где с=17. Следовательно, CН = 17 √ 2 . . = 17 √ 2 2 . . .
Рассмотрим прямоугольный треугольник АВМ, где угол В равен 30 градусов, а катет АМ= CН= 17 √ 2 2 . . . Зная, что катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы, найдем АВ (она будет в два раза больше катета). АВ=2 × 17 √ 2 2 . . =17 √ 2
Ответ: см. решение
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.

Для нахождения площади трапеции в справочном материале есть формула
S = a + b 2 . . h , для которой у нас известны и основания, и высота. Подставим в неё эти значения и вычислим: S = 7 + 11 2 . . ∙ 7 = 18 2 . . ∙ 7 = 9 ∙ 7 = 63
pазбирался: Даниил Романович | обсудить разбор | оценить
Радиус вписанной в квадрат окружности равен 22 √ 2 . Найти диагональ этого квадрата.

Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.

Обозначим диагональ АВ, точкой О – центр окружности, С – один из углов квадрата. Покажем расстояние от центра окружности до стороны квадрата – радиус r. Если радиус равен 22 √ 2 , то сторона квадрата будет в два раза больше, т.е. 44 √ 2 .
Рассмотрим прямоугольный треугольник АВС, который является равнобедренным (так как по условию дан квадрат) и боковые стороны равны по 44 √ 2 . Нам надо найти диагональ, т.е. гипотенузу данного треугольника. Вспомним, что для нахождения гипотенузы равнобедренного треугольника есть формула с=а √ 2 , где с – гипотенуза, а – катет. Подставим в неё наши данные:
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь четырехугольника можно вычислить по формуле S= d 1 d 2 s i n a 2 . . , где d 1 и d 2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d 1 , если d 2 =16, sin a= 2 5 . . , a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8= d 1 × 16 × 2 5 . . 2 . .
В правой части можно сократить 16 и 2 на 2: 12,8= d 1 × 8 × 2 5 . . 1 . .
Теперь умножим 8 на дробь 2 5 . . , получим 3,2: 12,8= d 1 × 3 , 2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить

На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).

Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.

Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).

Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
Читайте также:

