Как сделать интервал в маткаде

Обновлено: 03.07.2024

Простейший способ найти корень уравнения с одним неизвестным обеспечит функция root ( ). Аргументами функции root ( ) являются вид функции определяющей решаемое уравнение и имя переменой, относительно которой ищется решение – root (f(x),x) Если уравнение содержит несколько корней, то функция обеспечивает нахождение единственного корня, ближайшего к заданному начальному значению для искомой переменной. Точность вычислений может быть увеличена или уменьшена посредством задания значения переменной TOL, равной по умолчанию 10-3 и определённой в меню Math, Options (Математика, Опции). Установленное значение TOL также оказывает влияние на точность вычислений.

Уравнение с одним неизвестным: функция root

Для решения уравнения с одним неизвестным в Mathcad, помимо вычислительного блока Given/Find, предусмотрена встроенная функция root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, использует разные алгоритмы поиска корней.

root(f(x),x);
root (f (x), x, a, b):
- f(x) – скалярная функция, определяющая уравнение f(x)=0;
- х – имя скалярной переменной, относительно которой решается уравнение;
- а, b – границы интервала, внутри которого происходит поиск корня.
Первый тип функции root, аналогично встроенной функции Find, требует дополнительного задания начального значения переменной х, для чего нужно просто перед применением функции root присвоить х некоторое число. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня, т. к. поиск корня будет производиться вблизи этого числа. Пример работы функции root объясняется листингом 5.13.

Листинг 5.13. Два варианта уравнения методом секущих:

В чем же отличие встроенной функции Find от функции root? Оно состоит в том, что для решения одних и тех же задач используются различные численные алгоритмы (градиентные и метод секущих соответственно). В примерах уравнений с одним неизвестным, которые мы рассматривали до сего момента, выбор метода не влиял на окончательный результат, поскольку фигурировавшие в них функции были “хорошими”, т. е. достаточно гладкими для поиска корня одним из градиентных методов, требующих, как известно, вычисления производных. Между тем бывают ситуации, когда применение того или иного метода имеет решающее значение.

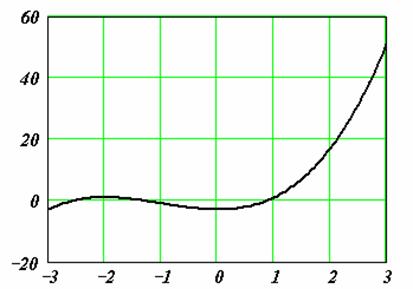
Приведем пример простой функции f(x), корни которой удается отыскать только при помощи функции root (листинг 5.14). Она определена в первой строке этого листинга, а ее корень вычислен во второй строке. Из графика, представленного на рис. 5.5, видно, что f (х) имеет особенность в окрестности своего корня, являясь в ней разрывной. В завершающей части листинга 5.14 предпринимается попытка отыскать нулевое значение f (х) посредством вычислительного блока Given/Find, которая оказывается неудачной.

Если Вы заметили ошибку, выделите, пожалуйста, необходимый текст и нажмите CTRL + Enter, чтобы сообщить об этом редактору.

Решение нелинейных уравнений

Вычисление корней численными методами включает два основных этапа:

· уточнение корней до заданной точности.

Рассмотрим эти два этапа подробно.

Отделение корней нелинейного уравнения

Учитывая легкость построения графиков функций в MathCAD , в дальнейшем будет использоваться графический метод отделения корней.

Пример. Дано алгебраическое уравнение

Определить интервалы локализации корней этого уравнения.

Пример. Дано алгебраическое уравнение

Определить интервалы локализации корней этого уравнения.

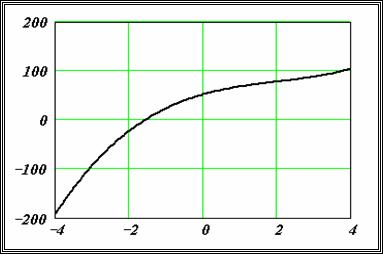
На рисунке приведен график функции , построенный в MathCAD . Видно, что в качестве интервала изоляции можно принять интервал . Однако уравнение имеет три корня. Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨

Уточнение корней нелинейного уравнения

Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.

Функция root . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. или , где – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению, – скалярная переменная, относительно которой решается уравнение, – границы интервала локализации корня.

Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.

Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨

Функция root с двумя аргументами требует задания (до обращения к функции) переменной начального значения корня из интервала локализации.

Пример 8.1.5. Используя функцию root , вычислить изменения корня нелинейного уравнения при изменении коэффициента а от 1 до 10 с шагом 1.

Функция polyroots . Для вычисления всех корней алгебраического уравнения порядка (не выше 5) рекомендуется использовать функцию polyroots . Обращение к этой функции имеет вид polyroots (v) , где v – вектор, состоящий из n +1 проекций, равных коэффициентам алгебраического уравнения, т.е. . Эта функция не требует проведения процедуры локализации корней.

Пример. Используя функцию polyroots , найти все три корня уравнения , включая и два комплексных

Блок Given . При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given , имеющий следующую структуру:

Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.

Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find ( x ), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которая возвращает приближенное значение корня.

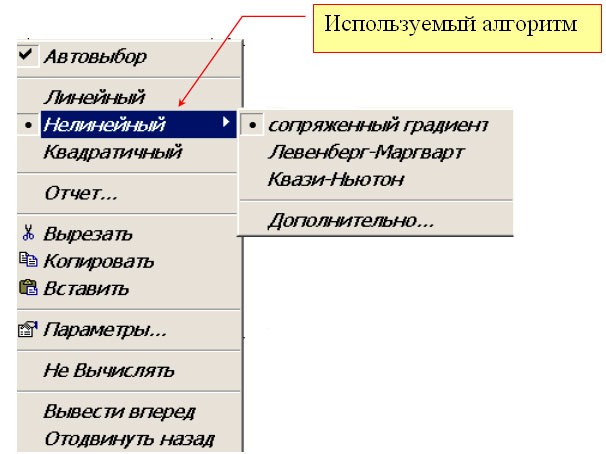
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find ( x ) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.

Аналогично можно задать алгоритм решения и для функции Minerr ( x ).

Использование численных методов в функциях Find ( x ), Minerr ( x ) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.

Пример. Используя блок Given , вычислите корень уравнения в интервале отделения .

7+1. Odesolve

Итак, задача 4. На моторной лодке, движущейся со скоростью v, заглушили мотор. Спрашивается, как будут меняться скорость лодки и пройденный ею путь? Задача предельно упрощена – на лодку действует сила трения, пропорциональная квадрату скорости лодки (см. рис. 14, 15, 16 и 17, где этот квадрат фигурировал). На рисунке 18 показано решение и графическое отображение этой задачи с помощью функции Odesolve.

Рис. 18. Решение задачи об остановки лодки

Коэффициент пропорциональности, записанный в уравнении на рис. 18 (масса лодки, помноженная на ускорение – на первую производную скорости по времени), состоит из двух частей, связанных с трением о воздух надводной части лодки и трением о воду ее подводной части. Эти коэффициенты пропорциональны плотности ρ среды (воздуха или воды) и площади поперечного сечения надводной и подводной частей лодки S.

Задачу об остановке моторной лодки мы решили численно: функция Odesolve не ищет аналитического решения уравнения. Она формирует таблицу значений искомых функций v (скорость лодки) и x (пройденный путь), по которым интерполяцией создается непрерывная функция, по которой мы построили графики (см. рис. 18).

Рис. 19. Символьное решение дифференциального уравнения

[1]Первое действие: как долго лодка была бы в пути, если б вода в реке была неподвижна – 2*10 км/12 км/ч = 1 час 40 минут; второе действие… Читатель, докончи это решение сам и сравни с теми, которые приведены ниже. Мы по действиям такие задачи решали когда-то в 5 классе школы. Но не всякая задача может быть решена по действиям. Поэтому и была придумана алгебра. Эту задачу тоже сходу нельзя решить пошагово. В древние времена, пока не было формулы корней квадратного уравнения, не всякое квадратное уравнение могли решить, причем решения были очень хитроумными.

[2] На этом и некоторых других рисунках будут показаны инструменты Mathcad Prime и Mathcad 15 для решения описываемых задач.

[4] Навстречу друг другу по одноколейной дороге одновременно вышли два поезда. И не столкнулись. Почему? Ответ: не судьба! 😉

[6] Самые быстроходные суда те, у которых подводная часть минимальна: глиссирующие суда, суда на подводных крыльях или на воздушной подушке.

Решение систем уравнений

В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:

· алгебраические системы уравнений;

· трансцендентные системы уравнений.

Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).

Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

В матричном виде систему можно записать как

где – матрица размерности , – вектор с проекциями.

Для вычисления решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, – вектор правой части.

Решение систем нелинейных уравнений

MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD 2001 i доведено до 200.

Для решения системы уравнений необходимо выполнить следующие этапы.

Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.

Пример. Дана система уравнений:

Определить начальные приближения для решений этой системы.

Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨

Вычисление решения системы уравнений с заданной точностью . Для этого используется уже известный вычислительный блок Given .

Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find ( x ), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке . Число аргументов функции должно быть равно числу неизвестных.

Следующие выражения недопустимы внутри блока решения:

· ограничения со знаком ¹ ;

· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;

· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr ).

Пример. Используя блок Given , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.

Mathcad является универсальным инструментом у тех людей, которые плотно связали свою жизнь с вычислениями. "Маткад" способен производить сложные математические расчеты и мгновенно выдавать ответ на экране. Студенты или те, кто в первый раз столкнулся с этой программой, задают множество вопросов, на которые не могут дать ответ самостоятельно. Один из них, затрудняющий дальнейшее обучение: как построить график в "Маткаде"? На самом деле, это не так сложно, как может показаться. Постараемся разобраться также в том, как в "Маткаде" построить график функции, как строить несколько функций, узнаем о некоторых элементах отображение графика на экране.

Быстрый график в Mathcad

Вам будет интересно: Пуристы - это. Значение слова

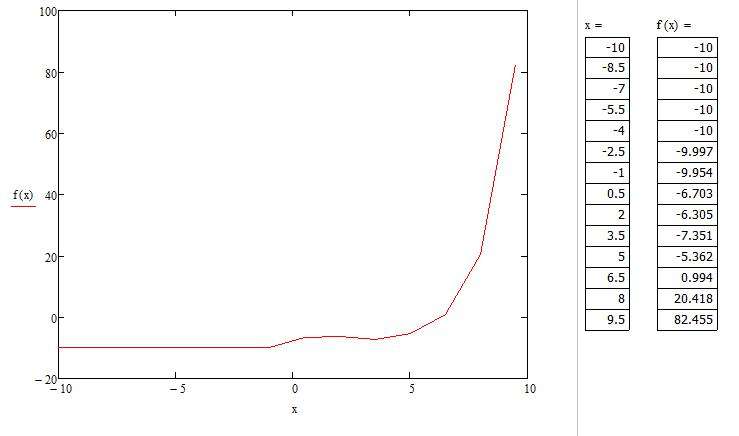
Возьмем одну функцию и будем проводить все ниже перечисленные операции с ней. Допустим, имеем следующее техническое задание: построить график функции f(x) = (e^x/(2x-1)^2)-10 на интервале [-10;10], исследовать поведение функции.

Итак, перед тем как построить график в "Маткаде", нужно переписать нашу функцию в математическую среду. После этого просто прикинем возможный график без масштабирования и всего прочего.

Построение дополнительных графиков

Чтобы понять, как построить несколько графиков в "Маткаде", добавим к нашему техническому заданию небольшое дополнение: построить график производной от заданной функции. Единственное, что нам нужно - в поле графика добавить производную по переменной "x".

График, построенный по набору значений

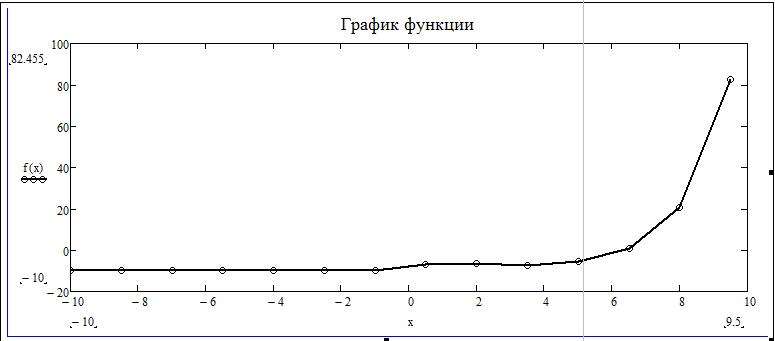
Перед тем как построить график в "Маткаде" по точкам, необходимо создать диапазон значений. Сразу отметим, что график, построенный по точкам, иногда бывает неточным, так как может найтись такая точка, которая не попадет в диапазон значений, но в оригинальном графике в ней происходит разрыв. В этом примере специально будет показан этот случай.

Мы видим, что на графике, построенном по точкам, не отображается та точка, которая осуществляет разрыв на исходном графике. То есть можно сделать вывод о том, что построение по точкам может не учитывать значения функции, которые создают разрыв.

Настройка отображения графика

В этой статье мы уже затрагивали настройки графика. Окно с настройками вызывается двойным нажатием левой кнопкой мыши по графику. В окне форматирования графика есть пять разделов. "Оси X, Y" - содержит информацию про координатные оси, а также отображения вспомогательных элементов. Второй раздел "Трассировка" связан с кривыми линиями построения графика, здесь можно корректировать их толщину, цвет и другое. "Формат числа" отвечает за отображение и расчет единиц. В четвертом разделе можно добавлять подписи. Пятый раздел " По умолчанию" выводит все настройки в стандартную форму.

Скалярные операции над векторами и матрицами, если это не оговорено особо, производятся независимо над их каждым элементом, как над скаляром.

Таблица П3.2. Вычислительные операторы

Вычисление n-й производной

Сумма ранжированной переменной

Произведение ранжированной переменной

Таблица ПЗ.З. Встроенные функции по алфавиту

Обратная тригонометрическая или гиперболическая функция *

Функция Эйри первого рода

х,у — координаты точки

Угол между точкой и осью ОХ

file— строковое представление пути к файлу

Дозапись данных в существующий текстовый файл

z — аргумент функции

Аргумент комплексного числа

х,у — координаты точки

Угол, отсчитываемый от оси ОХ до точки (х,у)

А,В,С. — векторы или матрицы

Слияние матриц слева направо

n — порядок х — аргумент

Мнимая и действительная части функции Бесселя —Кельвина

Функция Эйри второго рода

х,у — векторы данных

и — вектор значений сшивок В-сплайнов

n — порядок полиномов

Вектор коэффициентов В-сплайна

Bulstoer (y0, t0, t1, M, D)

Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера

bulstoer (y0, t0, t1, acc, D, k, s)

Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера (для определения только последней точки интервала)

Bvalf it (z1, z2, x0, x1, xf, D, load1, load2, score)

zl,z2 — вектор начальных значений для недостающих левых и правых граничных условий

хО — левая граница xl — правая граница xf — внутренняя точка

D(x,y) — векторная функция, задающая систему ОДУ

Возвращает вектор недостающих граничных условий у краевой задачи для системы N ОДУ с дополнительным условием в промежуточной точке

loadl (xO , z ) , Ioad2 (xl , z ) -векторные функции, задающие левые и правые граничные условия

score (xf , у ) — векторная функция, задающая сшивку решений в xf

Наименьшее целое, не меньшее х

у — вектор данных

Вектор прямого комплексного преобразования Фурье (в разных нормировках)

А — квадратная, определенная матрица

А — матрица или вектор

Объединение строковых переменных

А — квадратная матрица

А — матрица i — индекс столбца

Сортировка строк матрицы по элементам 1-го столбца

CreateMesh (F, s0, s1, t0, t1, sgr, tgr, fmap)

F ( s , t ) — векторная функция из трех элементов

tO.tl — пределы! sO.sl — пределы s

tgr, sgr — число точек сетки по t и s

fmap— функция преобразования координат

Создание вложенного массива, представляющего х-, у- и z -координаты параметрической поверхности, заданной функцией F

Cre-ateSpace(F[, t0, t1, tgr, fmap])

F(t) — векторная функция из трех элементов

to.tl — пределы t

tgr — число точек сетки по t

fmap— функция преобразования координат

Создание вложенного массива, представляющего х-, у- и z -координаты параметрической пространственной кривой, заданной функцией F

Комплексный знак числа

х,у — векторы данных

Вектор коэффициентов кубического сплайна

r,6,z— цилиндрические координаты

Преобразование цилиндрических координат в прямоугольные

х— значение случайной величины

par — список параметров распределения *

Плотность вероятности со статистикой распределения *

Диагональная матрица, на диагонали которой находятся элементы вектора

А — квадратная матрица

Собственные значения матрицы

А — квадратная матрица

А. — собственное значение

Собственный вектор матрицы, соответствующий заданному собственному значению

А — квадратная матрица

Собственные векторы матрицы

Обратная функция ошибок

Экспонента в степени z

x,y — векторы данных

g — вектор начальных значений а,Ь,с

у — вектор данных

Вектор прямого преобразования Фурье (в разных нормировках)

а,Ь,с — параметры х — аргумент, -1 0

Функция Бесселя второго рода нулевого, первого и m-го порядка

n — порядок х — аргумент

Сферическая функция Бесселя второго рода

Некоторые функции, составляющие семейства типовых функций, приведены в сокращенном виде с недостающей частью имени в виде звездочки *. Например, различные статистические функции, описывающие различные распределения, или функции вывода в файлы. Подробные сведения содержатся в разделе, на который указывает соответствующая ссылка.

Знаете ли Вы, что любой разумный человек скажет, что не может быть улыбки без кота и дыма без огня, что-то там, в космосе, должно быть, теплое, излучающее ЭМ-волны, соответствующее температуре 2.7ºК. Действительно, наблюдаемое космическое микроволновое излучение (CMB) есть тепловое излучение частиц эфира, имеющих температуру 2.7ºK. Еще в начале ХХ века великие химики и физики Д. И. Менделеев и Вальтер Нернст предсказали, что такое излучение (температура) должно обнаруживаться в космосе. В 1933 году проф. Эрих Регенер из Штуттгарта с помощью стратосферных зондов измерил эту температуру. Его измерения дали 2.8ºK - практически точное современное значение. Подробнее читайте в FAQ по эфирной физике.

БлогNot. Методы решения нелинейных уравнений в MathCAD

Методы решения нелинейных уравнений в MathCAD

Реализуем для некоторого уравнения 4 наиболее популярных численных метода для решения нелинейных уравнений. При этом мы стремимся именно запрограммировать методы, а не воспользоваться встроенным инструментом Given. Find или функциями root , polyroot . Об этих способах решения почитайте, например, здесь.

Определим функцию уравнения f(x)=0 как функцию пользователя, интервал поиска решения зададим переменными a и b . Найти этот интервал можно, например, табличным или графическим методом:

Уравнение и интервал поиска решения

Начальный интервал [a,b] должен быть таким, чтобы значения f(a) и f(b) имели противоположные знаки. Если искомый корень уравнения окажется единственным на интервале, то совсем хорошо :)

Логика метода дихотомии (возможно, более правильные названия - метод бисекции, метод половинного деления) довольно проста: если на концах выбранного интервала [a,b] знаки функции совпадают (произведение f(a)*f(b)>0 ), то вернуть результат "недопустимый интервал" (вернём в этом случае ответ "бесконечность"), в противном случае до тех пор, пока длина интервала не станет меньше заданной погрешности ε , будем находить середину текущего интервала c=(a+b)/2 , считать в ней значение функции и проверять, какую из половин отрезка [a,c] или [c,b] нужно отбросить для выполнения следующего шага - а именно, ту, в которой знак f(c) совпадает со знаком функции на левой или правой границе интервала (в листинге - проверка f(a)*f(c)>0 ). Для большей точности вернём середину "последнего" интервала [a,b] , меньшего ε :

Метод дихотомии в MathCAD

В методе простой итерации исходное уравнение f(x)=0 представляется в эквивалентном виде φ(x)=x (что, вообще говоря, можно сделать бесконечным числом способов), а затем шаг метода выполняется по формуле x_k+1 = φ(x_k) , пока не будет достигнута заданная точность |x_k+1-x_k| . Если выбрать φ(x)=x-c*f(x) , то константу c целесообразнее всего искать методом релаксации, для которого c=2/(M+m) , где M - максимальное из значений первой производной на концах отрезка или в находящихся на нём точках перегиба функции (точках, где f''(x)=0 ), а m - минимальное из таких значений. Вот соответствующий расчёт в MathCAD:

Метод простой итерации (релаксации) в MathCAD

Если заданной сходимости нет в течение 10000 шагов, в подпрограмме предусмотрен аварийный выход.

Численный метод Ньютона решения нелинейного уравнения основан на формуле вида x_k+1 = x_k-f(x_k)/f'(x_k) , обеспечивающей наилучшую сходимость, но требующей дополнительного вычисления производной на каждом шаге. Так как производные для MathCAD - не проблема, можно всё сделать "в лоб":

Метод Ньютона для решения нелинейного уравнения в MathCAD

Видно, что сходимость метода - на 2 порядка выше (погрешность найденного решения ~ 10 -8 ).

Наконец, существует метод хорд, в котором кривая f(x) заменяется прямой линией (хордой), стягивающей точки (a, f(a)) и (b, f(b)) . Формула этого метода зависит от знака выражения f(a)*f''(a) , то есть, имеет два варианта:
Если f(a)*f''(a)>0 , то x₀=b , x_k+1=a-(f(a)(x_k-a))/(f(x_k)-f(a))
Если f(a)*f''(a) , то x₀=a , x_k+1=x_k-(f(x_k)*(b-x_k))/(f(b)-f(x_k))

Вот примерная реализация на MathCAD, как и в предыдущих двух случаях, контролируется максимальное число итераций, равное 10000:

Метод хорд решения нелинейного уравнения в MathCAD

Видно, что сходимость метода оказалась в нашем случае не столь высока.

Подсчитать, сколько шагов какому методу потребовалось, можете сами, немного поменяв выдачу подпрограмм.

Читайте также:

Как сделать интервал в маткаде

Уравнение с одним неизвестным: функция root

Решение нелинейных уравнений

Отделение корней нелинейного уравнения

Уточнение корней нелинейного уравнения

7+1. Odesolve

Решение систем уравнений

Системы линейных алгебраических уравнений

Решение систем нелинейных уравнений

Быстрый график в Mathcad

Построение дополнительных графиков

График, построенный по набору значений

Настройка отображения графика

Методы решения нелинейных уравнений в MathCAD