Как сделать интерфейс для программы на c метод половинного деления

Добавил пользователь Евгений Кузнецов
Обновлено: 04.10.2024

Спасибо,но я уже был на этой ссылке. но увы она мне мало что дала. я могу решить ээто уравнение обычным способом..но ввиде программы для меня это темный лес ((

Репутация: 62

Репутация: 55

сам алгоритм метода понятен? то есть вручную этим методом решить сможешь?

по ссылке же программа готовая есть, кстати.

сам алгоритм метода понятен? то есть вручную этим методом решить сможешь?

по ссылке же программа готовая есть, кстати.

Репутация: 0

ну чтобы выводила все три.
обычно, с помощью точек экстремума находят промежутки, на которых функция меняет знак. Например, одна точка экстремума 5 а вторая -5. Таким образом, где-то между ними функция была равна нулю. В этом промежутке корень и ищут.

Репутация: 0

ну чтобы выводила все три.
обычно, с помощью точек экстремума находят промежутки, на которых функция меняет знак.

А подробнее можно? Желательно с кодом.

Репутация: 0

Ну с кодом-то мы все не против))

Точка экстремума, это точка, где функция меняет свое стремление. Между точками 1 и 2 функция стремится вниз, а между точками 2 и 3 она стремится вверх. Поэтому точка 2 является производной. Собственно все отмеченные здесь точки являются экстремумами.

Тебе нужно найти точки экстремума, и если точка 1 и 2 имеют разные знаки, значит на этом отрезке функция прошла через ноль, значит, здесь и стоит искать корень.

Де-факто, точки экстремума - это нули производной. Отсюда вытекает: чтобы найти экстремумы, надо найти производную от твоего уравнения и приравнять к нулю.
НО среди полученных корней может оказаться "мусор". Чтобы понять, какие точки экстремальны, необходимо посмотреть знаки промежутков. Если знаки до точки и после точки различны, то точка является экстремумом

Репутация: 0

Я знаю как найти экстремумы, но как это описать в Паскале и приделать к своей программе пока не могу сообразить.

Репутация: 0

Если ты найдешь производную от кубического уравнения, получишь квадратное Неужели, в самом деле сложно решить квадратное уравнение? Я думаю, что производную можно найти и вручную

Репутация: 0

Квадратное уравнение я знаю как решать, но как это все к своему коду приделать пока не пойму.

где f(x) — заданная алгебраическая или трансцендентная функция.

Решить уравнение — значит найти все его корни, то есть те значения x , которые обращают уравнение в тождество.
Если уравнение достаточно сложно, то задача точного определения корней является в некоторых случаях нерешаемой. Поэтому ставится задача найти такое приближенное значение корня x_ПP , которое отличается от точного значения корня x* на величину, по модулю не превышающую указанной точности (малой положительной величины) ε , то есть

│x* – x_пр │ ε также называют допустимой ошибкой , которую можно задать по своему усмотрению.

Этапы приближенного решения нелинейных уравнений

Приближенное решение уравнения состоит из двух этапов:

Отделение корней, то есть нахождение интервалов из области определения функции f(x) , в каждом из которых содержится только один корень уравнения f(x)=0 .
Уточнение корней до заданной точности.

Отделение корней

Отделение корней можно проводить графически и аналитически.
Для того чтобы графически отделить корни уравнения, необходимо построить график функции f(x) . Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения.

Для примера рассмотрим задачу решения уравнения

где угол x задан в градусах. Указанное уравнение можно переписать в виде

Для графического отсечения корней достаточно построить график функции

Из рисунка видно, что корень уравнения лежит в промежутке x∈(6;8) .

Аналитическое отделение корней

Аналитическое отделение корней основано на следующих теоремах.
Теорема 1 . Если непрерывная функция f(x) принимает на концах отрезка [a; b] значения разных знаков, т.е.

то на этом отрезке содержится по крайней мере один корень уравнения.
Теорема 2 . Если непрерывная на отрезке [a; b] функция f(x) принимает на концах отрезка значения разных знаков, а производная f'(x) сохраняет знак внутри указанного отрезка, то внутри отрезка существует единственный корень уравнения f(x) = 0 .

Уточнение корней

Для уточнения корней может использоваться один из следующих методов:

Метод последовательных приближений (метод итераций)

Метод итерации — численный метод решения математических задач, используемый для приближённого решения алгебраических уравнений и систем. Суть метода заключается в нахождении по приближённому значению величины следующего приближения (являющегося более точным). Метод позволяет получить решение с заданной точностью в виде предела последовательности итераций. Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения решения.
Функциональное уравнение может быть записано в виде

Функцию f(x) называют сжимающим отображением .

Последовательность чисел x₀, x₁ ,…, x_n называется итерационной , если для любого номера n>0 элемент x_n выражается через элемент x_n-1 по рекуррентной формуле

а в качестве x₀ взято любое число из области задания функции f(x) .

Реализация на C++ для рассмотренного выше примера

Уравнение может быть записано в форме

Метод Ньютона (метод касательных)

Если известно начальное приближение x₀ корня уравнения f(x)=0, то последовательные приближения находят по формуле

Графическая интерпретация метода касательных имеет вид

Реализация на C++
Для заданного уравнения

производная будет иметь вид

Результат выполнения

Метод секущих (метод хорд)

Если x₀ , x₁ - приближенные значения корня уравнения f(x) = 0 и выполняется условие

то последующие приближения находят по формуле

Методом хорд называют также метод, при котором один из концов отрезка закреплен, т.е. вычисление приближения корня уравнения f(x) = 0 производят по формулам:

Геометрическая интерпретация метода хорд:

Реализация на C++
В отличие от двух рассмотренных выше методов, метод хорд предполагает наличие двух начальных приближений, представляющих собой концы отрезка, внутри которого располагается искомый корень.

Результат выполнения

Метод половинного деления (метод дихотомии)

Если x₀ , x₁ - приближенные значения корня уравнения f(x) = 0 и выполняется условие

то последующие приближения находятся по формуле

и вычисляется f(x_i) . Если f(x_i)=0 , то корень найден. В противном случае из отрезков выбирается тот, на концах которого f(x) принимает значения разных знаков, и проделывается аналогичная операция. Процесс продолжается до получения требуемой точности.

Геометрическая интерпретация метода дихотомии

Реализация на C++

Результат выполнения

Для численного поиска решения также можно использовать генетические алгоритмы.

Существует довольно очевидная теорема: "Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у нее есть корень (как минимум, один, но м.б. и несколько)". На базе этой теоремы построено численное нахождение приближенного значения корня функции. Обобщенно этот метод называется дихотомией, т.е. делением отрезка на две части. Обобщенный алгоритм выглядит так:

Задать начальный интервал ;
Убедиться, что на концах функция имеет разный знак;
Повторять
- выбрать внутри интервала точку ;
- сравнить знак функции в точке со знаком функции в одном из концов;
  - если совпадает, то переместить этот конец интервала в точку ,
  - иначе переместить в точку другой конец интервала;

Варианты метода дихотомии различаются выбором точки деления. Рассмотрим варианты дихотомии: метод половинного деления и метод хорд.

Метод половинного деления

Метод половинного деления известен также как метод бисекции. В данном методе интервал делится ровно пополам.

Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции - и это весьма важное свойство. Недостатком метода является то же самое - метод никогда не сойдется быстрее, т.е. сходимость метода всегда равна сходимости в наихудшем случае.

Метод половинного деления:

Один из простых способов поиска корней функции одного аргумента.
Применяется для нахождения значений действительно-значной функции, определяемому по какому-либо критерию (это может быть сравнение на минимум, максимум или конкретное число).

Метод половинного деления как метод поиска корней функции

Изложение метода

Перед применением метода для поиска корней функции необходимо отделить корни одним из известных способов, например, графическим методом. Отделение корней необходимо в случае, если неизвестно на каком отрезке нужно искать корень.

Будем считать, что корень функции отделён на отрезке . Задача заключается в том, чтобы найти и уточнить этот корень методом половинного деления. Другими словами, требуется найти приближённое значение корня с заданной точностью .

Пусть функция непрерывна на отрезке ,

и - единственный корень уравнения .

(Мы не рассматриваем случай, когда корней на отрезке несколько, то есть более одного. В качестве можно взять и другое достаточно малое положительное число, например, .)

Поделим отрезок пополам. Получим точку и два отрезка .

Если , то корень найден ().

Если нет, то из двух полученных отрезков и надо выбрать один такой, что , то есть

, если или
, если .

Для того, чтобы найти приближённое значение корня с точностью до , необходимо остановить процесс половинного деления на таком шаге , на котором и вычислить . Тогда можно взять .

Реализация метода на С++ и числовой пример

Решим уравнение методом половинного деления. Графическим методом находим отрезок , которому принадлежит искомый корень. Так как , то принимаем .

Ниже приведен пример программы на Си++, которая решает поставленную задачу.

Программа 1. Корень уравнения

Искомый корень . Вычисления проводились с точностью .

Промежуточные вычисления представлены в таблице ниже.

n	a_n	b_n	c_n	b_n-c_n
1	0	1	0.5	0.5
2	0.5	1	0.75	0.25
3	0.75	1	0.875	0.125
4	0.875	1	0.9375	0.0625
5	0.875	0.9375	0.90625	0.03125
6	0.875	0.90625	0.890625	0.015625
7	0.875	0.890625	0.8828125	0.0078125

Метод половинного деления как метод оптимизации

Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных.

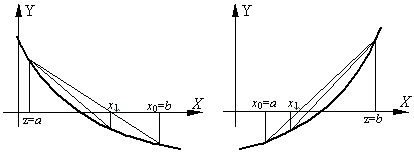
Рассмотрим метод половинного деления как простейший однопараметрический метод безусловной оптимизации. Данный метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.

Дана функция . Необходимо найти , доставляющий минимум (или максимум) функции на интервале с заданной точностью , т.е. найти

Запишем словесный алгоритм метода.

На каждом шаге процесса поиска делим отрезок пополам, - координата середины отрезка .
Вычисляем значение функции в окрестности вычисленной точки , т.е.
.
Сравниваем и и отбрасываем одну из половинок отрезка (рис. 1).
- При поиске минимума:
  - Если , то отбрасываем отрезок , тогда . (рис. 1.а)
  - Иначе отбрасываем отрезок , тогда . (рис. 1.б)
- При поиске максимума:
  - Если , то отбрасываем отрезок , тогда .
  - Иначе отбрасываем отрезок , тогда .
Деление отрезка продолжается, пока его длина не станет меньше заданной точности , т.е. .

Схема алгоритма метода представлена на рис 2.

При выводе – координата точки, в которой функция имеет минимум (или максимум), – значение функции в этой точке.

Метод хорд

Недостаток деления отрезка строго пополам проистекает от того, что он использует лишь знак функции, игноририруя отклонение (абсолютную величину). Но очевидно, что чем меньше (по абсолютной величине) значение функции, тем ближе мы находимся к корню. Метод хорд предлагает делить отрезок в точке, отстоящей от краев отрезка пропорционально абсолютному значению функции на краях. (Название "метод хорд" происходит от того, что точка деления является пересечением отрезка - хорды - с осью абцисс.)

Изложение метода

Метод основан на замене функции на каждом шаге поиска хордой, пересечение которой с осью дает приближение корня.

При этом в процессе поиска семейство хорд может строиться:

при фиксированном левом конце хорд, т.е. , тогда начальная точка (рис. 3а);
при фиксированном правом конце хорд, т.е. , тогда начальная точка (рис. 3б);

В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:

Процесс поиска продолжается до тех пор, пока не выполнится условие или .

Метод обеспечивает быструю сходимость, если , т.е. хорды фиксируются в том конце интервала , где знаки функции и ее кривизны совпадают.

Схема алгоритма уточнения корня методом хорд представлена на рис. 4.

Комбинация метода хорд и метода половинного деления

Метод хорд можно применить в качестве "последнего штриха" после того, как метод половинного деления гарантирует требуемую точность - это не улучшит существенно гарантируемой точности, но, скорее всего, на несколько порядков повысит точность решения.

Если применять аналогичное уточнение к интервалу, полученному методом хорд, то эффект будет значительно слабее. Это ещё раз иллюстрирует тот факт, что метод хорд очень хорошо работает в условиях малого интервала (близости обеих границ интервала к корню), но неспособен сам создать себе эти условия (приблизить обе границы к корню).

На вопрос о том, стоит ли использовать попеременное применение метода половинного деления и метода хорд, ответ отрицателен. После того, как метод хорд приближает одну из границ почти вплотную к корню, методу половинного деления придётся долго работать, чтобы гарантировать заданную точность, т.к. метод хорд ее гарантировать не может.

Поэтому лучше использовать в качестве точки деления что-то среднее: если метод половинного деления предлагает использовать , а метод хорд - , то возьмем . Коэффициент .

Чему должен быть равен коэффициент ? Его следует не задавать, а вычислять по ходу работы: если при очередной операции интервал уменьшился более чем в два раза (это то, что гарантирует метод половинного деления), то значит, нужно больше доверять методу хорд (уменьшить ), и наоборот.

Может показаться, что при большом доверии к методу хорд этот комбинированный метод работает так же, как метод хорд. На самом деле, это не так: метод хорд передвигает по направлению к корню только одну границу, а комбинированный метод даже при высоком доверии к методу хорд передвигает и вторую границу, обеспечивая лучшие условия для работы метода хорд, а значит - для ещё большего доверия к нему.

Одной из главных задач в обучении является развитие творческих и исследовательских способностей учащихся. На уроках информатики применение компьютеров позволяет учащимся заниматься исследовательской работой при решении задач из различных областей (например, физические, математические, экономические задачи). При этом они должны научиться четко формулировать задачу, решать ее и оценивать полученный результат.

Использование новых информационных технологий позволяет решать некоторые задачи нетрадиционными способами, а также решать прикладные задачи, которые ранее не могли рассматриваться в силу сложности математического аппарата. Так, в школьном курсе математики учащиеся рассматривают уравнения, которые имеют точные решения. Однако в реальной практике решение большинства уравнений не может быть записано в явном виде. Их решение находится только приближенными методами. Ранее способы решения таких уравнений рассматривались после изучения одного из алгоритмических языков. Во-первых, разрабатывали алгоритм метода решения (например, итерации, половинного деления). Во-вторых, составляли программу и использовали ее для получения решения и его исследования. Труднее было при изучении темы "Моделирование", когда рассматривали задачи оптимизации. Задачи должны были быть довольно простыми, допускающими только одну поисковую переменную.

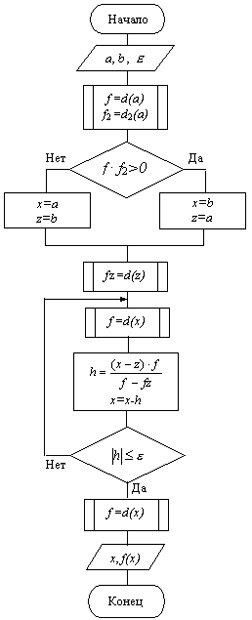
Метод половинного деления

Метод половинного деления или дихотомии (дихотомия - сопоставленность или противопоставленность двух частей целого) при нахождении корня уравнения f(x)=0 состоит в делении пополам отрезка [a; b], где находится корень. Затем анализируется изменение знака функции на половинных отрезках, и одна из границ отрезка [a; b] переносится в его середину. Переносится та граница, со стороны которой функция на половине отрезка знака не меняет. Далее процесс повторяется. Итерации прекращаются при выполнении одного из условий: либо длина интервала [a; b] становится меньше заданной погрешности нахождения корня ε, либо функция попадает в полосу шума ε1 – значение функции сравнимо с погрешностью расчетов.

Сначала поставим задачу. Дана монотонная, непрерывная функция f(x), которая содержит корень на отрезке [a,b], где b>a. Определить корень с точностью ε, если известно, что f(a)*f(b) 0, то теперь точкой a станет c: a=c; Если d ε, то идем в пункт 1) если нет, то корень с нужной нам точностью найден, и он равен: x=(a+b)/2;

Информатике трудно существовать в школе как отдельной науке, она должна помогать другим учебным предметам в развитии познавательного интереса к предмету, в решении логических задач, в обработке результатов лабораторных работ и индивидуальных практических заданий. Школьники начинают испытывать удовлетворение, замечая, что элементы математики и информатики имеют реальное воплощение в физических процессах.

Математика является необходимой базой, которая позволяет глубже вникнуть в суть описываемых физических явлений и закономерностей. Hа уроках физики развиваются и конкретизируются многие математические понятия: функции, графики, уравнения, неравенство, производная, интеграл, вектор и др. Это требует согласованных действий от учителя физики и математики при формировании общих понятий.

В применении информатики к преподаванию других предметов используются в основном две формы работы: привлечение программных средств для контроля знаний учащихся и работа учащихся с обучающими программами. В стороне остаются возможности составления программ самими учащимися для решения тех или иных задач, например, из области физики. Среди методистов распространено мнение, что подобная работа в школе возможна лишь на высоком уровне (в специализированных классах) из-за слабой подготовки учащихся в области программирования. Однако при согласованных действиях преподавателей физики, математики и информатики этот недостаток может быть легко выполнен. В частности успешным оказывается проведение уроков по теме "Движение тела под действием силы тяжести при начальной скорости управления горизонтально или под углом к горизонту", изучаемой в курсе физики 9 класса совместно с учителем информатики. В курсе информатики Учащимся предлагается лабораторная работа "Артиллериская задача". При выполнении данной работы учитель отрабатывает навыки программирования, изучает метод дихотомии (половинного деления). При этом приходится решать задачу физически, т.е. возникают трудности по применению формул физики. Таким образом затмевается главная цель урока по информатике: формирование умений и навыков решения задач методом половинного деления с использованием ЭВМ. Поэтому здесь и необходимо проведение интегрированных уроков по физике и информатике при решении задач. Тем более, что в Сборник задач по физике для 9-11 классов (переизданного в 1992 г.), автором которого является А.П. Рымкевич, включены программируемые задачи, которые для решения требуют знаний по физике и информатике.

Идея метода состоит в выборе точности решения и сведении первоначального отрезка [А;В], на котором существует корень уравнения, к отрезку заданной точности. Процесс сводится к последовательному делению отрезков пополам точкой С=(А+В)/2 и отбрасыванию той половины отрезка ([А;С] или [С;В]), на котором корня нет.

Выбор нужной половины отрезка основывается на проверке знаков значений функции на его краях. Выбирается та половина, на которой произведение значений функции на краях отрицательно, то есть где функция пересекает ось абсцисс.

Процесс продолжается до тех пор, пока длина отрезка не станет меньше удвоенной точности. Деление этого отрезка пополам дает значение корня х=(А+В)/2 с заданной точностью. (Объяснение материала сопровождается презентацией)

Приближенное решение уравнений с помощью электронных таблиц Excel.

Задача: решить уравнение x 3 =cosx

Чтобы решить уравнение графически, введем функцию у= x 3 - cosx

На интерактивной доске демонстрируется таблица значений функции на промежутке

[-2,5; 2,5] с шагом h=0,5 (заготовлена заранее). Построим график этой функции. На промежутке (-2,5; 2,5) график имеет одну точку пересечения с осью абсцисс, значит, на этом промежутке уравнение имеет один корень.

Разработка компьютерной модели нахождения корня уравнения на языке Visual Basic (Приложение 3)

Проект “Приближенное решение уравнения” (Приложение1)

1. Поместить на форму текстовые поля для ввода числовых значений концов отрезка А и В, поле для ввода точности вычислений и поле для вывода значений корня.

2. Поместить на форму кнопку и создать событийную процедуру, вычисляющую корень уравнения методом половинного деления:

Private Sub Комманда1_Click()

dblC = (dblA + dblB) / 2

If (dblA ^ 3 - Cos(dblA)) * (dblC ^ 3 - Cos(dblC)) dblE

Текст8.Text = (dblA + dblB) / 2

Закрепление материала. Проверка качества усвоения материала.

Работа на компьютерах. Учащиеся получают задание (Приложение 2) решить уравнения в Excel и проверить правильность выполнения задания, используя программу, разработанную на Visual Basic.

Определить корни уравнения графически. Уточнить один из корней уравнения с точностью e =0,1.

Читайте также: